Application of Variational Integrators in Modeling the Dynamics of Mechanical. Systems

1.

Application of Variational Integrators in
Modeling the Dynamics of Mechanical
Systems
Presented by Moiseev I.S.
IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering
St.Petersburg, 26-29 January 2021
1

2.

Modeling the dynamics of mechanical systems
Some advantages of modeling the dynamics
of mechanical systems over a physical
experiment:
• There is no need to produce an
experimental sample, which is especially
important in single-unit and small-scale
production
• The ability to conduct any number of
numerical experiments and obtain any
dynamic indicator of interest
• There is no possible danger, as opposed
to a physical experiment
• Relative cheapness in comparison with
experiments, for example, in the case of
testing machines at extreme and nonstandard modes due to the high cost of
samples or equipment
Illustration of physical experiments
(top) associated with danger and
requiring additional equipment in the
form of an outrigger and computer
simulation (bottom)
2

3.

Holonomic systems
An example of a holonomic
constraint is a mathematical
pendulum. The pendulum has
two degrees of freedom x and y
and a constant length equal to
the l. Then the constraint
equations will have the form:
x2 y 2 l 2 0
From this equation, we can
conclude that the constraint
depends solely on the
coordinates, and therefore is a
geometric constraint
3

4.

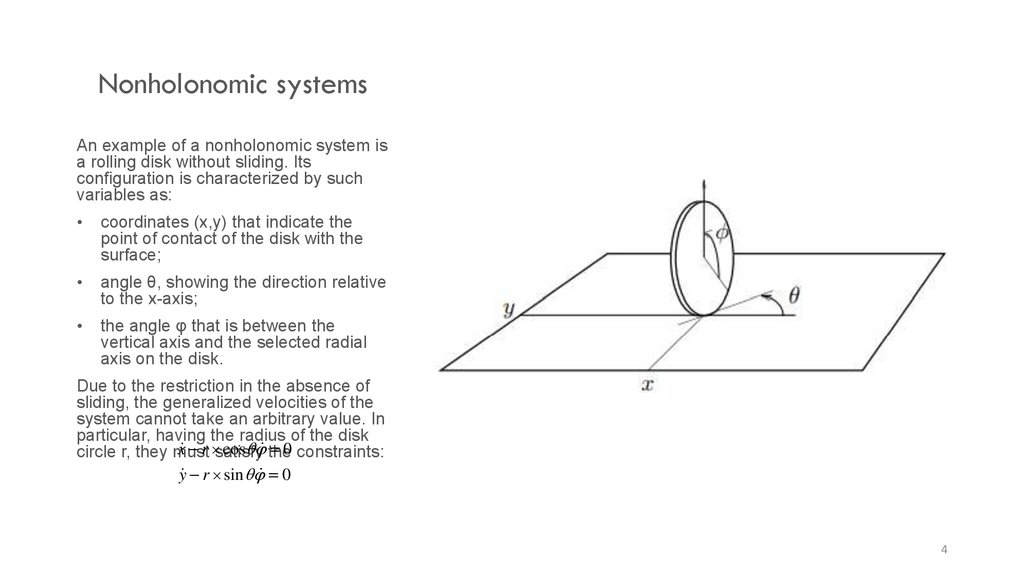
Nonholonomic systems
An example of a nonholonomic system is
a rolling disk without sliding. Its
configuration is characterized by such
variables as:
coordinates (x,y) that indicate the
point of contact of the disk with the
surface;
angle θ, showing the direction relative
to the x-axis;
the angle φ that is between the
vertical axis and the selected radial
axis on the disk.
Due to the restriction in the absence of
sliding, the generalized velocities of the
system cannot take an arbitrary value. In
particular, having the radius of the disk
x r satisfy
cos the
0 constraints:
circle r, they must
y r sin 0
4

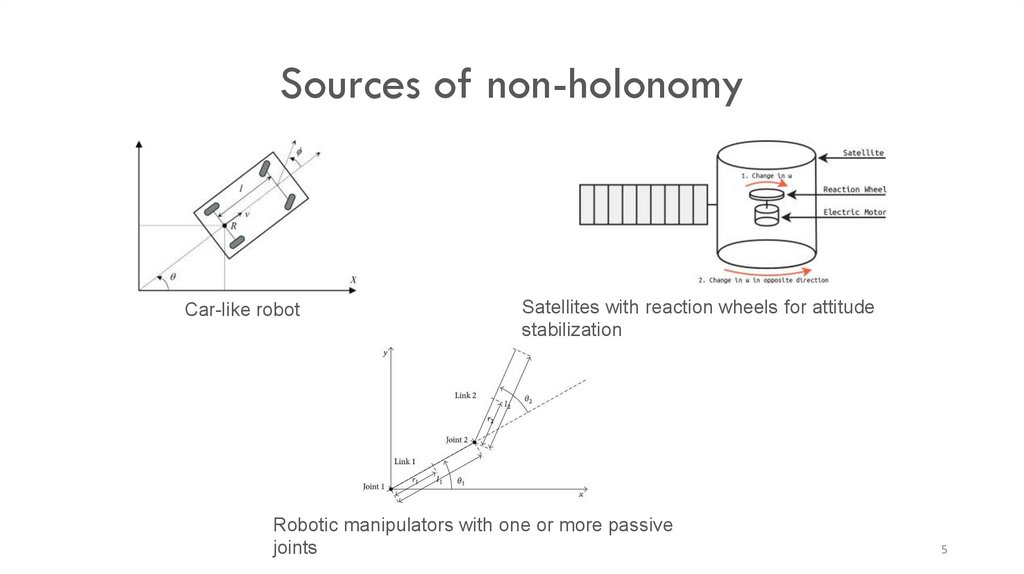
5.

Sources of non-holonomy
Car-like robot
Satellites with reaction wheels for attitude
stabilization
Robotic manipulators with one or more passive
joints
5

6.

Problems arising from the presence of
kinematic connections in nonholonomic systems
Since some kinematic connections in nonholonomic systems cannot be integrated and,
therefore, cannot be studied using classical theoretical mechanics, there is a need to find
other methods for studying the dynamics of such mechanical systems. In the article the
dynamics of mechanical systems is considered from the point of view of variational
principles.
6

7.

Hamilton's principle
The most essential form of the variational principle
for continuous mechanics belongs to William
Hamilton, and it is accordingly often called the
Hamilton principle or otherwise the principle of least
action. This principle declares that a dynamic
system will always find the shortest path between
two positions. The consequence of this is that
instead of viewing an object from the classical point
of view, in which it has acceleration in response to
applied forces, we can view it in a geometric sense.
Then the route along which the movement takes
place has optimal geometric attributes
William Rowan
Hamilton
1805 - 1865
7

8.

Advantages of the variational formulation
• First, the calculus of variations allows you to
convert problems set in derivatives from the
very beginning into an equivalent problem,
which, in comparison with the original form, is
usually much easier to solve. In the
variational definition, with additional
constraints, this transformation is usually
performed due to Lagrange multipliers. They
can be used to form a number of variational
principles similar to each other.
8

9.

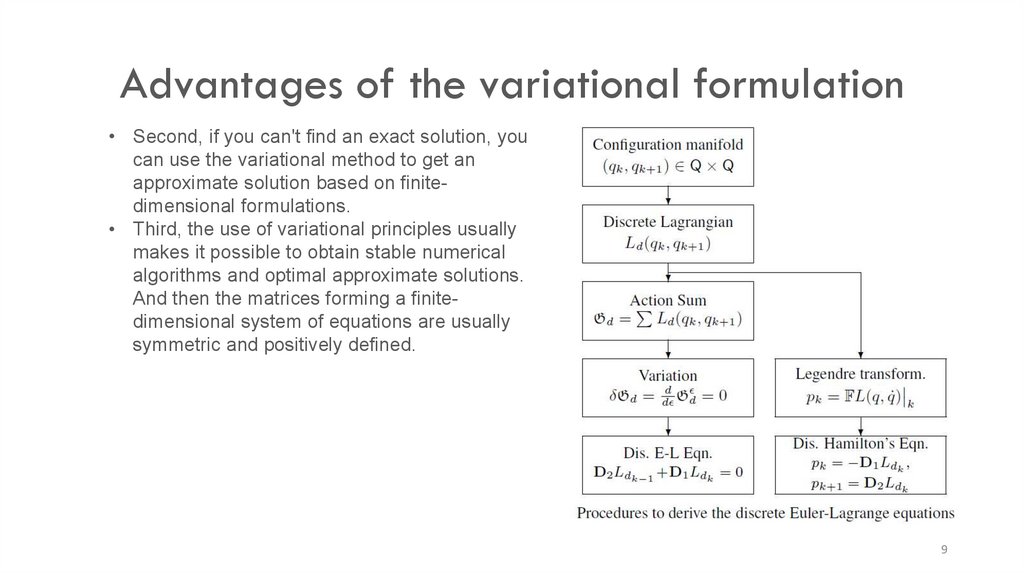
Advantages of the variational formulation
• Second, if you can't find an exact solution, you
can use the variational method to get an
approximate solution based on finitedimensional formulations.
• Third, the use of variational principles usually
makes it possible to obtain stable numerical
algorithms and optimal approximate solutions.
And then the matrices forming a finitedimensional system of equations are usually
symmetric and positively defined.
9

10.

Thank You!
Moiseev I.S.
10