Угол поворота. Радианная мера угла

1.

«Угол поворота.
Радианная мера угла»

2.

Немного из истории…
1. Древние вавилоняне и египтяне изучали
тригонометрию как часть астрономии;
разделили окружность на 360
2. Древние индийцы: ввели названия
«синус», «косинус», составили таблицы
синусов, косинусов
3. IX-XVвв – Средний и Ближний восток:
составляли таблицы котангенса, тангенса,
косеканса; ввели понятие единичной
окружности

3.

Немного из истории…
4. Насир ад-Дин Мухаммад ат-Туси (1201-
1274) выделил раздел тригонометрии из
астрономии
5. Лев Герсонид (1288-1344) – открыл теорему
синусов
6. XVII-XIXвв: применение тригономет-рии в
механике, физике, технике, как часть
математического анализа (Виетт, Бернулли) –
тригонометрические символы, графики –
синусоиды
7. Л.Эйлер: придал тригонометрии
современный вид

4.

Тригонометрия
(«три» - три, «гониа» - угол,
«метриа» - измеряю)
раздел математики,
изучающий соотношение
сторон и углов в
треугольнике

5.

Градусная мера угла
=1
1 – цена одного деления
окружности, разделенной на
360 частей

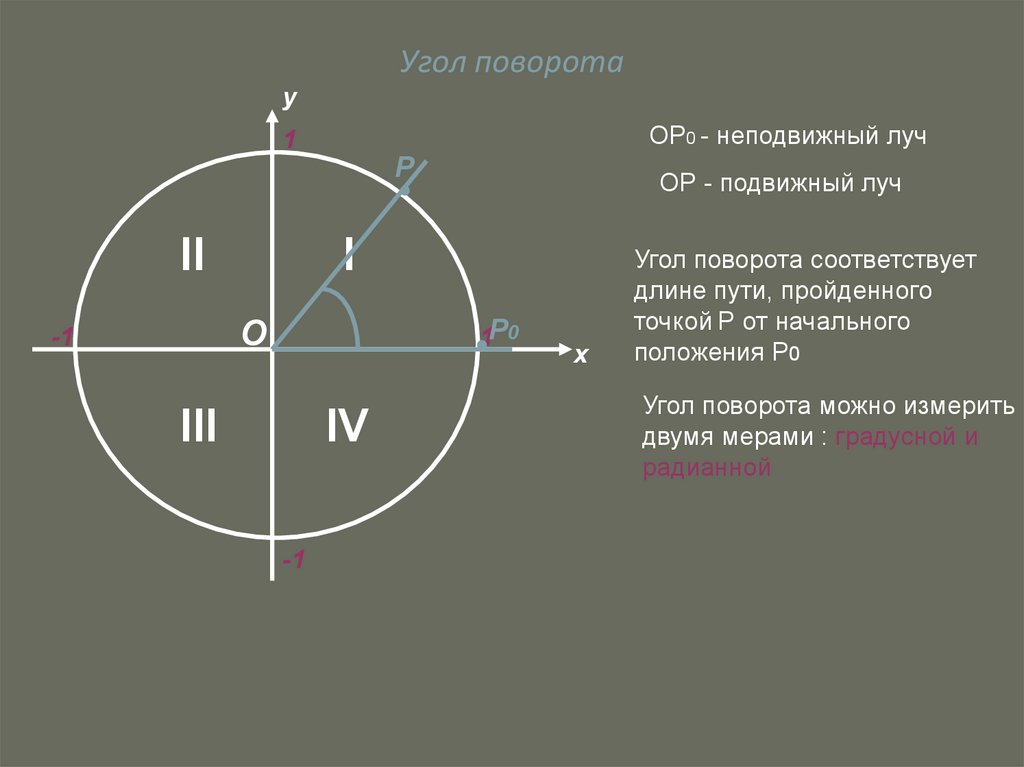
6. Угол поворота

у
ОР0 - неподвижный луч
1
II
Р
I
1Р0
О
-1
ОР - подвижный луч
III
IV
-1
х
Угол поворота соответствует
длине пути, пройденного
точкой Р от начального
положения Р0
Угол поворота можно измерить
двумя мерами : градусной и
радианной

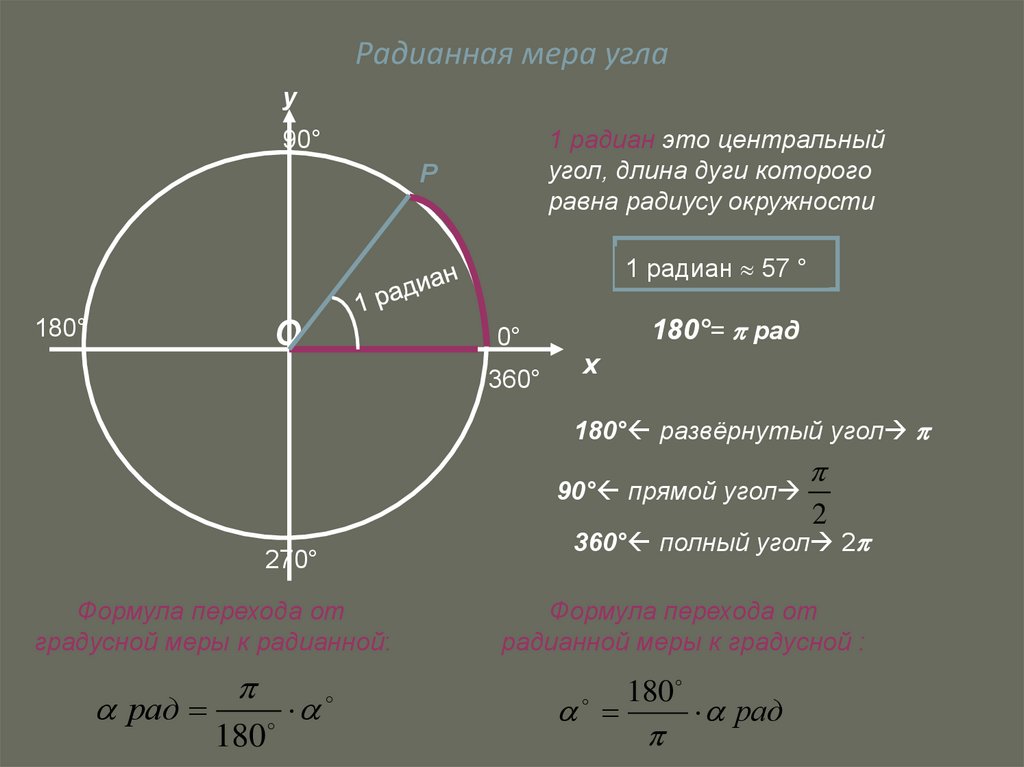
7. Радианная мера угла

у
1 радиан это центральный
угол, длина дуги которого
равна радиусу окружности
90°
Р
1 радиан 57 °
О
180°
0°
360°
180°= рад
х
180° развёрнутый угол
90° прямой угол
360° полный угол 2
270°
Формула перехода от
градусной меры к радианной:
рад
180
2
Формула перехода от
радианной меры к градусной :
180
рад

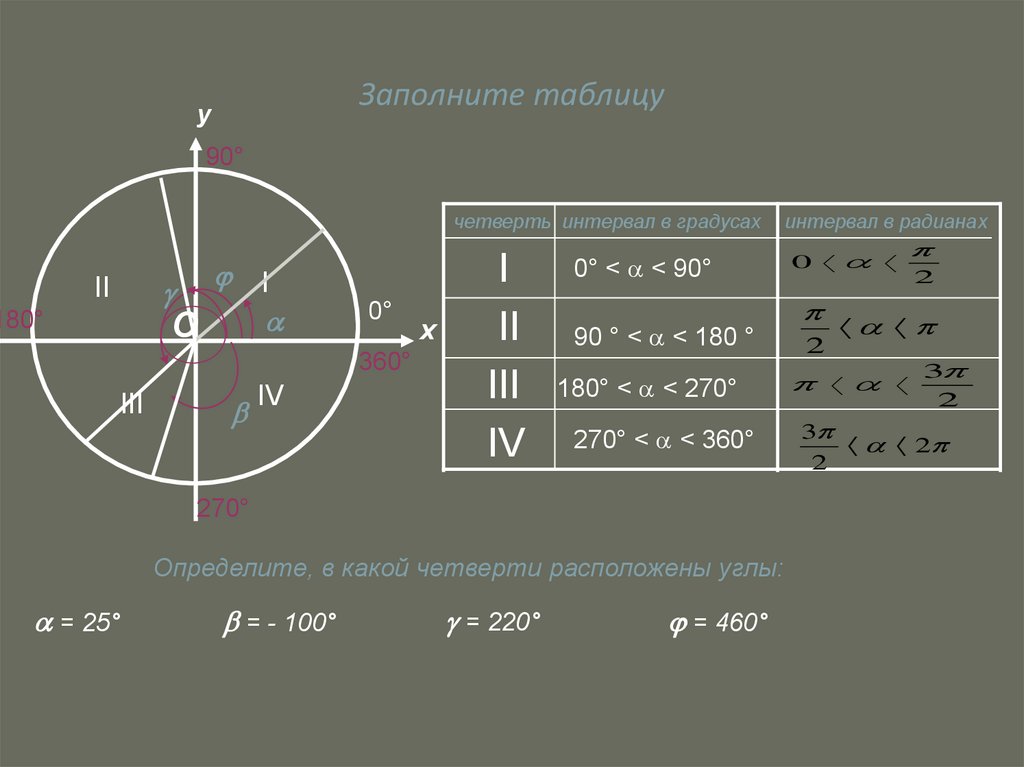
8. Заполните таблицу

у
90°
четверть интервал в градусах
I
25
О
II
180°
0°
360°
III
IV
х
I
II
III
IV
0° < < 90°
90 ° < < 180 °
180° < < 270°
270° < < 360°
270°
Определите, в какой четверти расположены углы:
= 25°
= - 100°
= 220°
= 460°
интервал в радианах
0
2
2
3
2
3
2
2

9.

Пример:
1. 30
30
рад.
рад.
6
180
90
рад
.
рад.
2. 90
180
2
3
135
рад
.
рад
.
3.135
4
180

10.

№1: Переведите в
радианную меру углы:
1) 45
4) 100
7) 215
2) 15
5) 200
8) 150
3) 72
6) 360
9) 330

11.

Пример:
1.
3
2.
4
4
3.
5
180
60
рад.
3
180
45
рад.
4
4 180
рад.
144
5

12.

№2: Переведите в
градусную меру углы:
7
1)
рад.
2
11
2)
рад.
4
7
3)
рад.
18
4)
рад.
3
5)
рад.
2
7
6)
рад.
4