Похожие презентации:
Математика. Раздел 6. Метод координат в пространстве. Занятие 62. Векторы в пространстве
1.
МатематикаРаздел 6. Метод координат в пространстве
Занятие 62.
Векторы в пространстве
2.
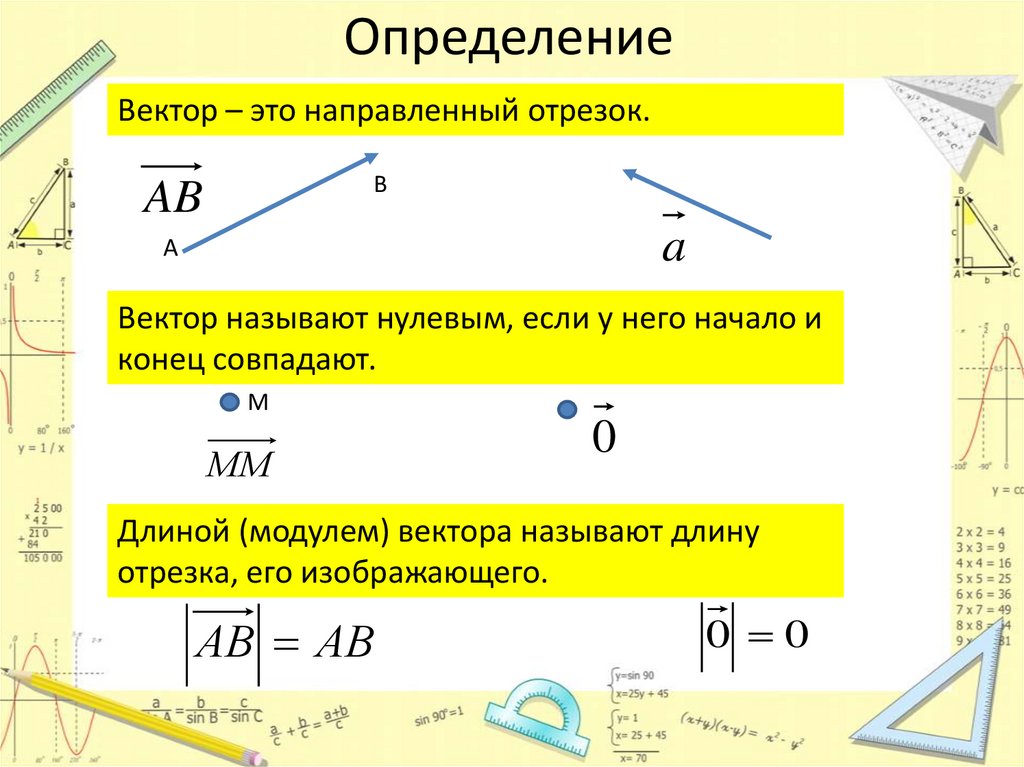
ОпределениеВектор – это направленный отрезок.
B
AB
a
A
Вектор называют нулевым, если у него начало и
конец совпадают.
М
ММ
0
Длиной (модулем) вектора называют длину
отрезка, его изображающего.
АВ АВ
0 0
3.
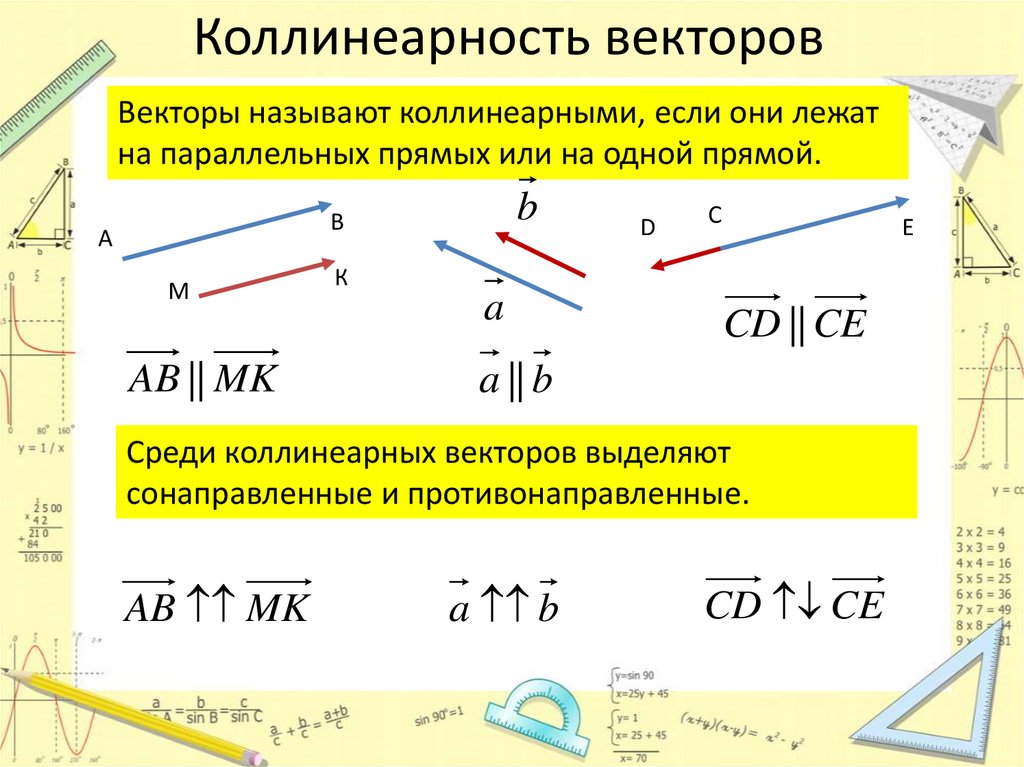
Коллинеарность векторовВекторы называют коллинеарными, если они лежат
на параллельных прямых или на одной прямой.
b
B
A
М
AB || MK
D
C
E
К
a
CD || CE
a || b
Среди коллинеарных векторов выделяют
сонаправленные и противонаправленные.
AB MK
a b
CD CE
4.
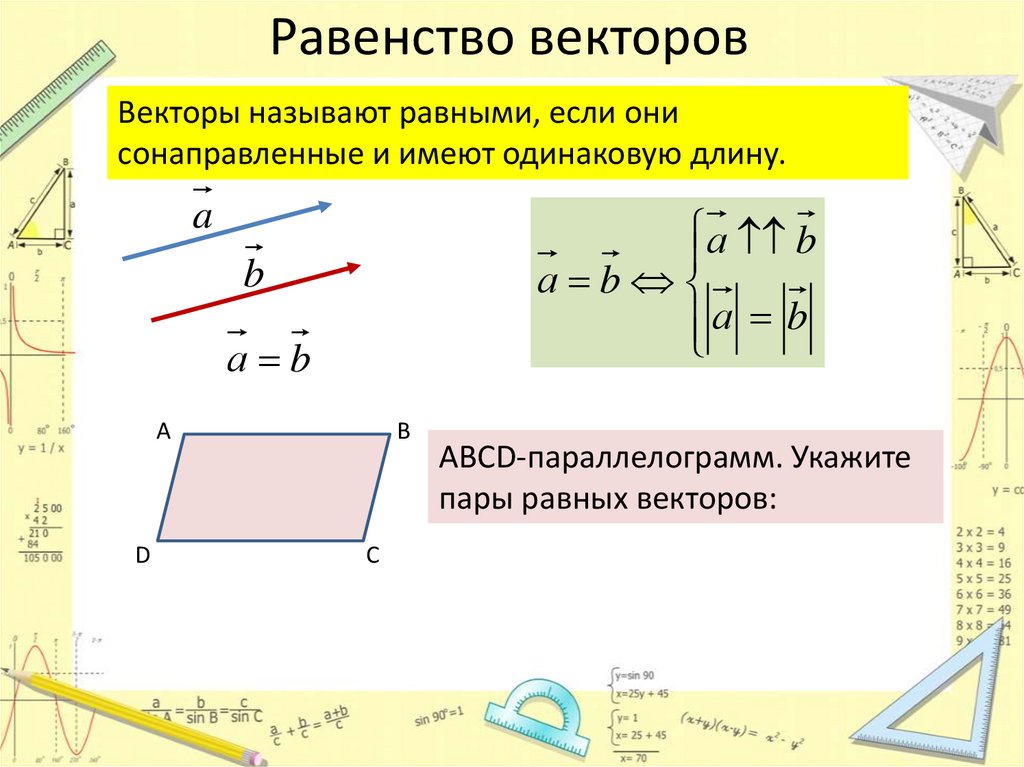
Равенство векторовВекторы называют равными, если они
сонаправленные и имеют одинаковую длину.
a
а b
а b
а b
b
а b
A
D
B
C
ABCD-параллелограмм. Укажите
пары равных векторов:
5.
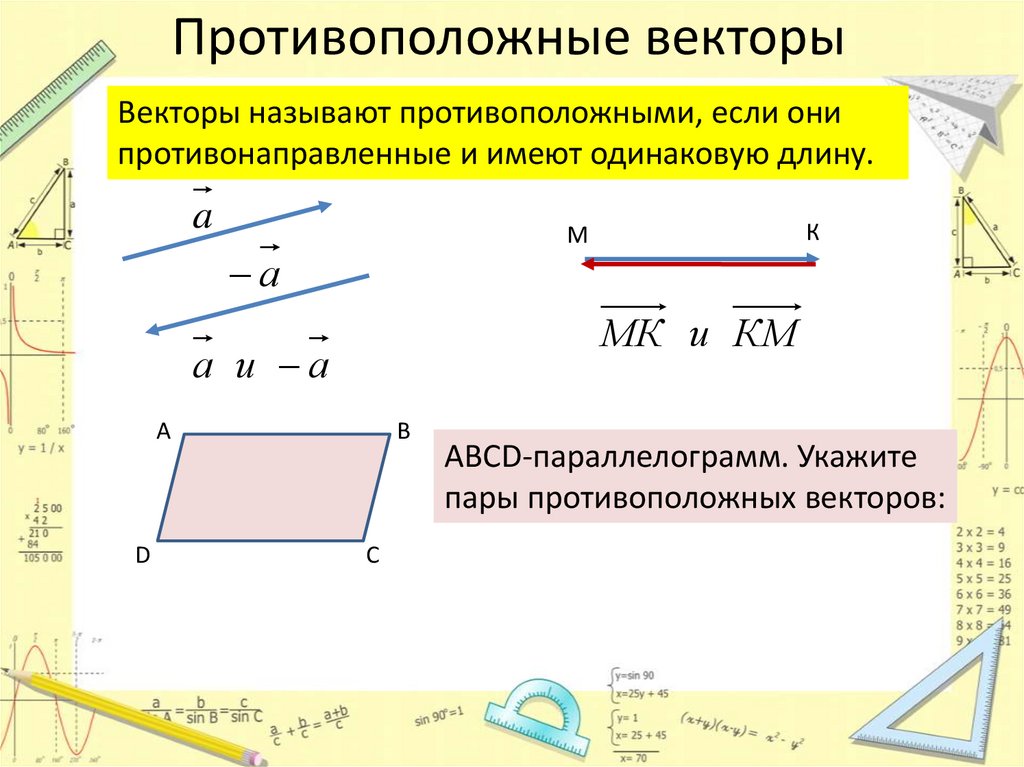
Противоположные векторыВекторы называют противоположными, если они
противонаправленные и имеют одинаковую длину.
a
а
МК и КМ
а и а
A
D
К
М
B
C
ABCD-параллелограмм. Укажите
пары противоположных векторов:
6.
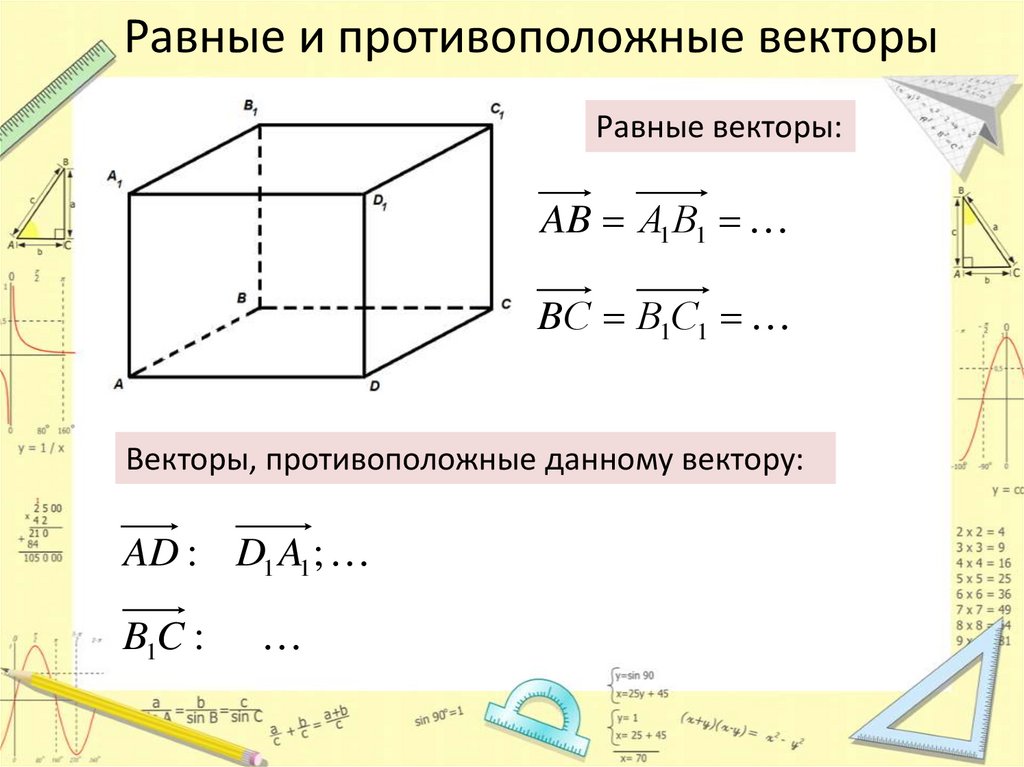
Равные и противоположные векторыРавные векторы:
AB А1 В1
BС В1С1
Векторы, противоположные данному вектору:
AD : D1 A1 ;
B1C :
7.
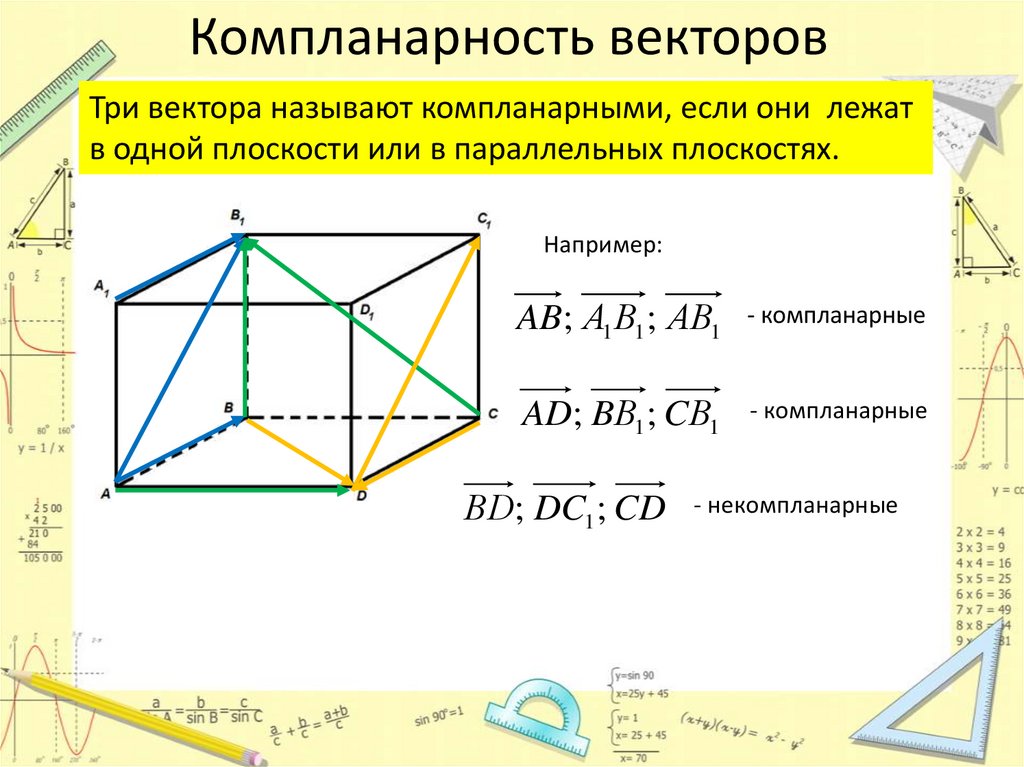
Компланарность векторовТри вектора называют компланарными, если они лежат
в одной плоскости или в параллельных плоскостях.
Например:
AB; А1 В1 ; АВ1
- компланарные
AD; BВ1 ; CВ1
- компланарные
ВD; DC1 ; CD
- некомпланарные
8.
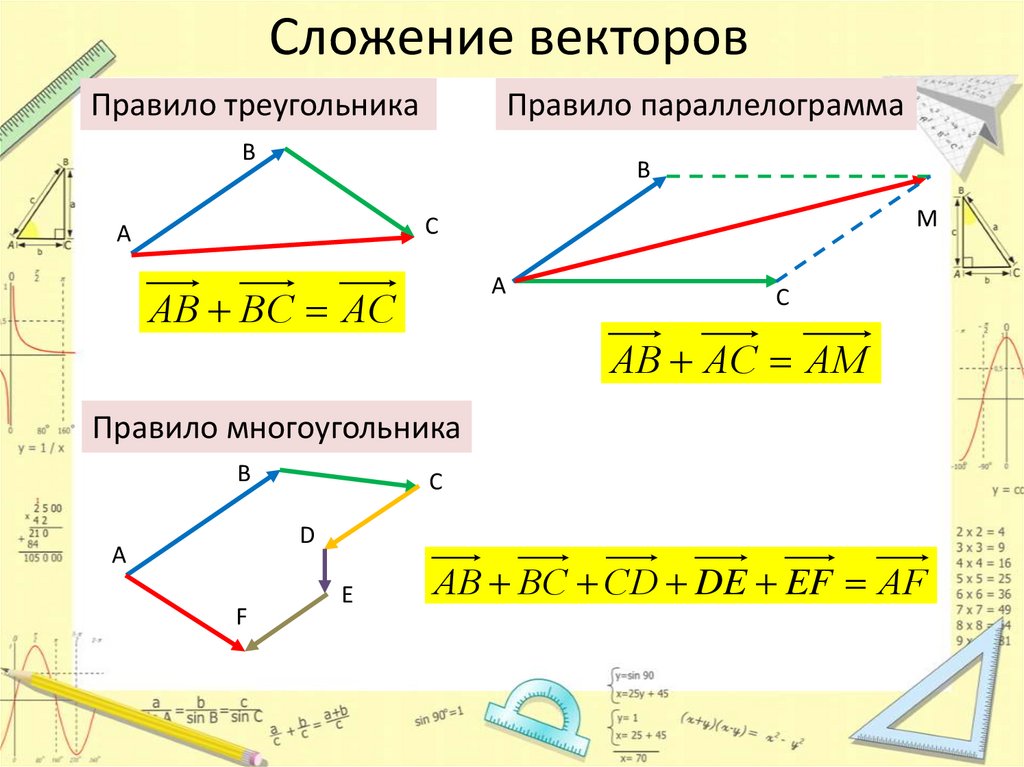
Сложение векторовПравило треугольника
Правило параллелограмма
В
В
М
С
A
A
АВ ВС АС
С
АВ АС АМ
Правило многоугольника
В
С
D
A
F
E
АВ ВС СD DE EF АF
9.
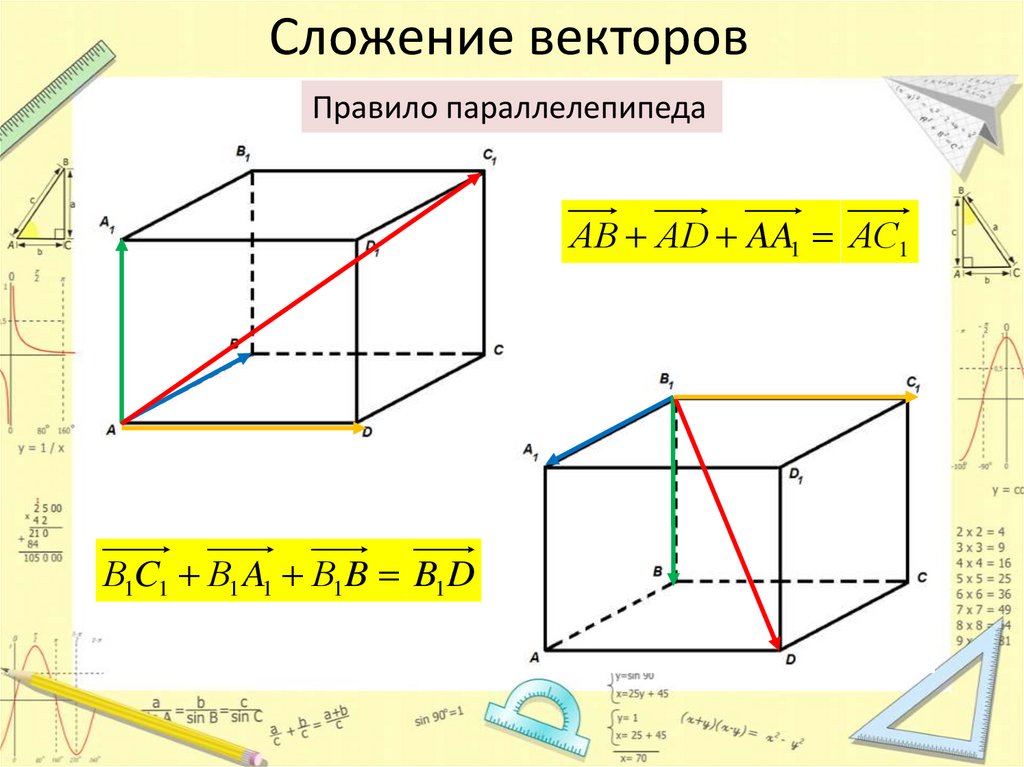
Сложение векторовПравило параллелепипеда
АВ АD AA1 АC1f
В1C1 В1 A1 В1 B B1 D
10.
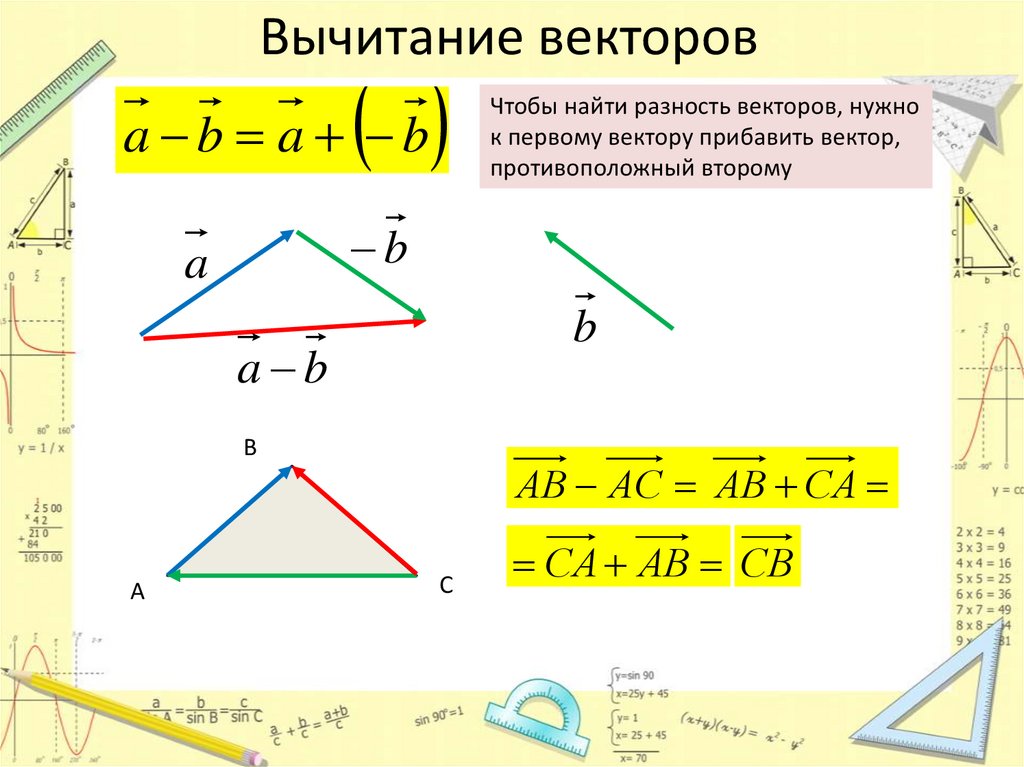
Вычитание векторовa b a b
b
a
b
a b
В
A
Чтобы найти разность векторов, нужно
к первому вектору прибавить вектор,
противоположный второму
АВ АС АВ СA
С
СA АВ СB
11.
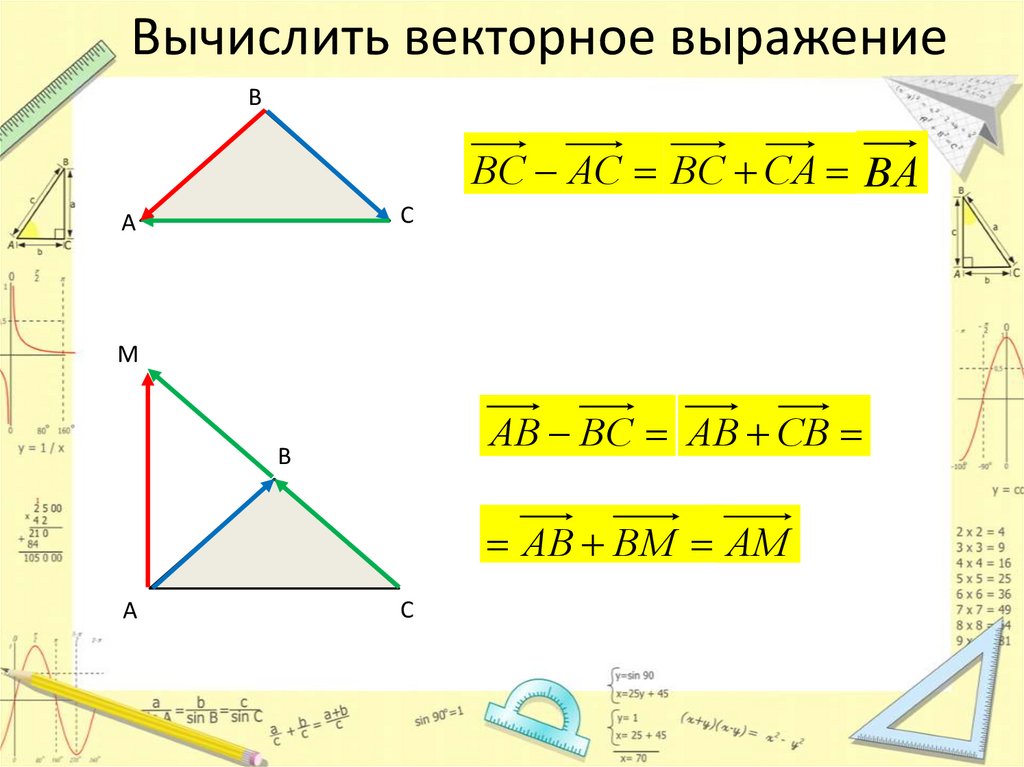
Вычислить векторное выражениеВ
ВС АС ВС СA BА
С
A
М
АВ ВС АВ СВ
В
АВ ВМ АМ
A
С
12.
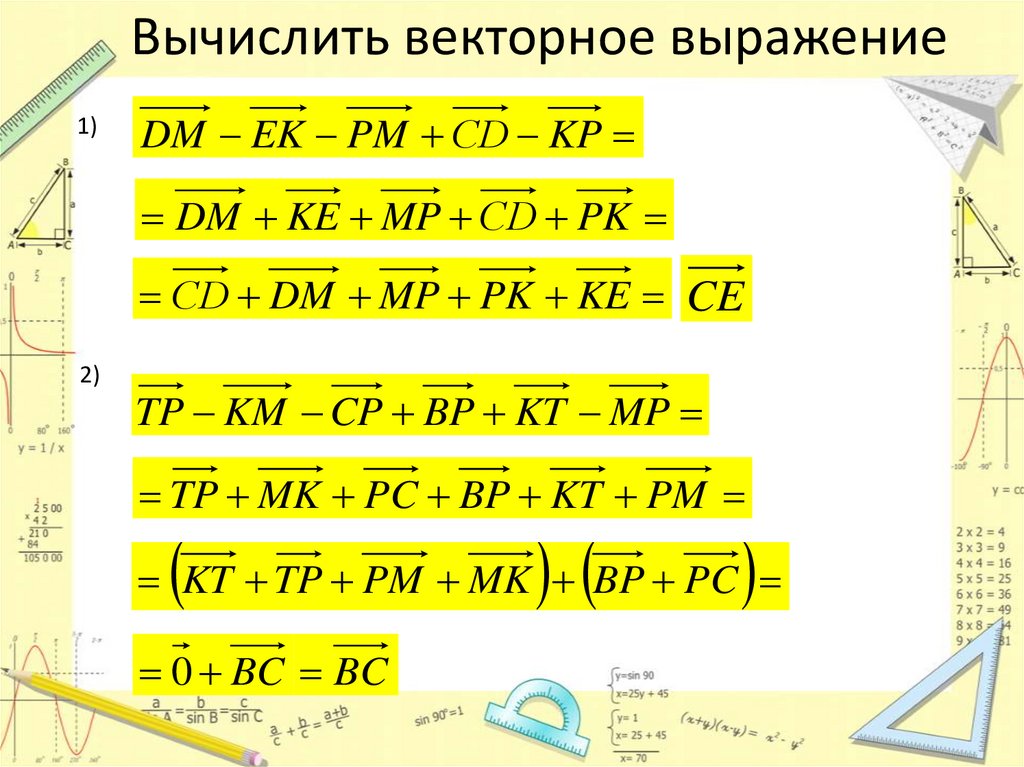
Вычислить векторное выражение1)
DM EK PM СD KP
DM KE MP СD PK
СD DM MP PK KE CE
2)
TP KM CP BP KT MP
TP MK PC BP KT PM
KT TP PM MK BP PC
0 BC BC
13.
Умножение вектора на числоb k a
b k а а b, если k 0
а b, если k 0
3a a a a
a
a
3a
a
a
2a 2 a a a
a a
2a
14.
Действия с векторамиДаны a и b . Построить p 5a 3b
a
b
Построение:
p 5a 3b 5a 3b
5a
p
3b
15.
Шмельков Владимир Юрьевичпреподаватель математики
ГБПОУ ЗКНО
Москва, 2021г.




 Математика
Математика








