Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов

1.

Математика
Раздел 6. Метод координат в пространстве
Занятие 63.
Координаты точек и векторов

2.

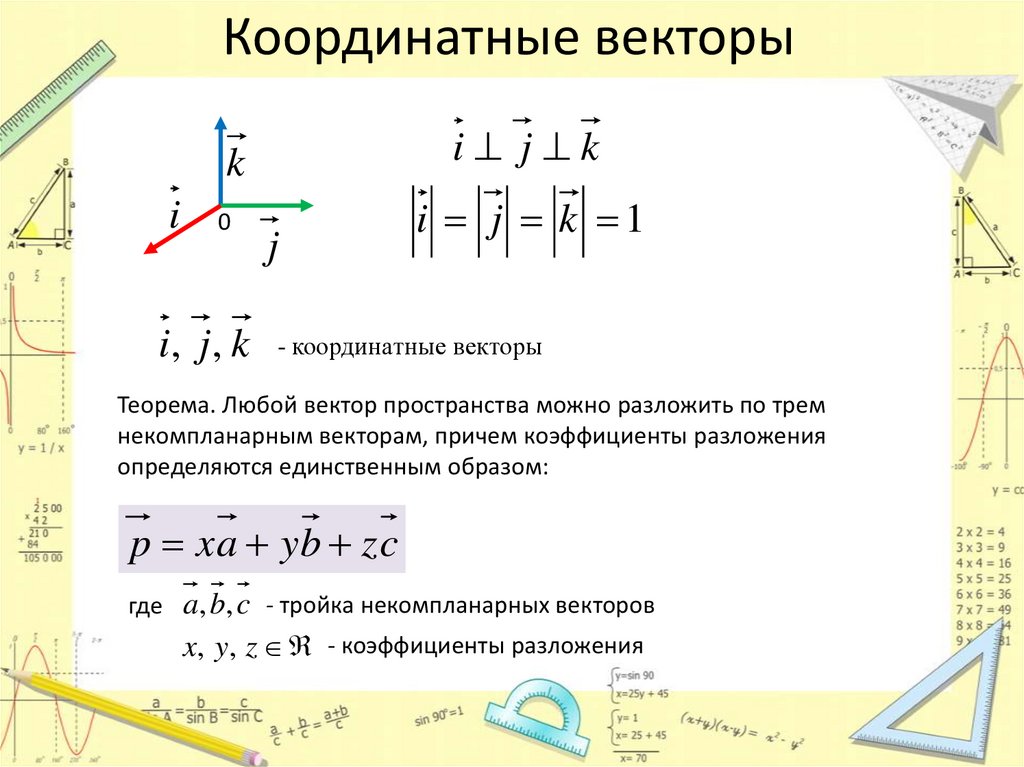
Координатные векторы
i j k
k
i
0
i, j , k
j
i j k 1
- координатные векторы
Теорема. Любой вектор пространства можно разложить по трем
некомпланарным векторам, причем коэффициенты разложения
определяются единственным образом:
p x a yb z c
где a, b, c - тройка некомпланарных векторов
x, y, z - коэффициенты разложения

3.

Координаты вектора
В качестве тройки некомпланарных векторов, по которым производится
разложение произвольного вектора, удобно выбрать координатные векторы
i, j , k
р
k
i
j
ОМ 2i 4 j 2k
т.о. x 2, y 4, z 2
ОМ xi y j z k
ОМ ОА ОВ ОС
ОА 2i
ОB 4 j
ОC 2k

4.

Координаты вектора
Координаты вектора равны коэффициентам разложения этого
вектора по координатным векторам, т.е.
p xi y j z k
p ( x; y; z )
Например:
а 3i j 2k
а (3;1;2)
b i 4 j 3k
b (1;4; 3) b (2; 5;0)
c 5i k
d 7j
c (5;0; 1)
d (0;7;0)
а ( 6;3;1)
а 6i 3 j k
b 2i 5 j
c (0; 1;3)
c j 3k
d (1; 2; 5)
?????

5.

Действия с векторами в координатах
Пусть даны
a ( x1 ; y1 ; z1 )
b ( x2 ; y 2 ; z 2 )
Тогда:
0. a b
x1 x2 ; y1 y2 ; z1 z 2
1. a b ( x1 x2 ; y1 y2 ; z1 z 2 )
2. a b ( x1 x2 ; y1 y2 ; z1 z 2 )
3. a ( x1 ; y1 ; z1 )

6.

Действия с векторами в координатах
Пусть даны a (3; 1;5)
Найти координаты вектора
b (2;1; 3)
c ( 4;0; 1)
р 3a 4b 5c
3
2
4
р 3a 4b 5с 3 1 4 1 5 0
5
3
1
3 3 2 4 4 5 9 8 20
1 3 1 4 0 5 3 4 0
5 3 3 4 1 5 15 12 5
Решение:
9 8 ( 20)
3 4 0
15 ( 12) ( 5)
37
1
8
Ответ:
р (37; 1; 8)

7.

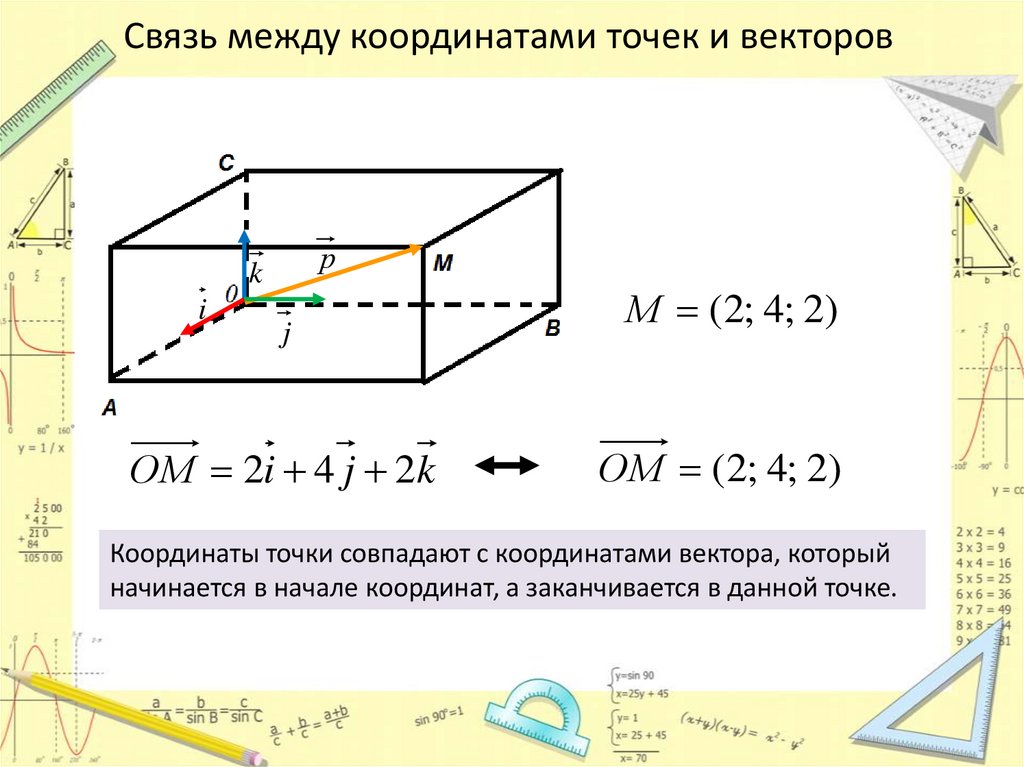
Связь между координатами точек и векторов
р
k
i
j
ОМ 2i 4 j 2k
М (2; 4; 2)
ОМ (2; 4; 2)
Координаты точки совпадают с координатами вектора, который
начинается в начале координат, а заканчивается в данной точке.

8.

Шмельков Владимир Юрьевич
преподаватель математики
ГБПОУ ЗКНО
Москва, 2021г.