Метод координат на плоскости

1.

Урок № 2
МЕТОД КООРДИНАТ НА
ПЛОСКОСТИ
ком
план
ар
ные

2.

Векторы
на плоскости
и
в пространстве
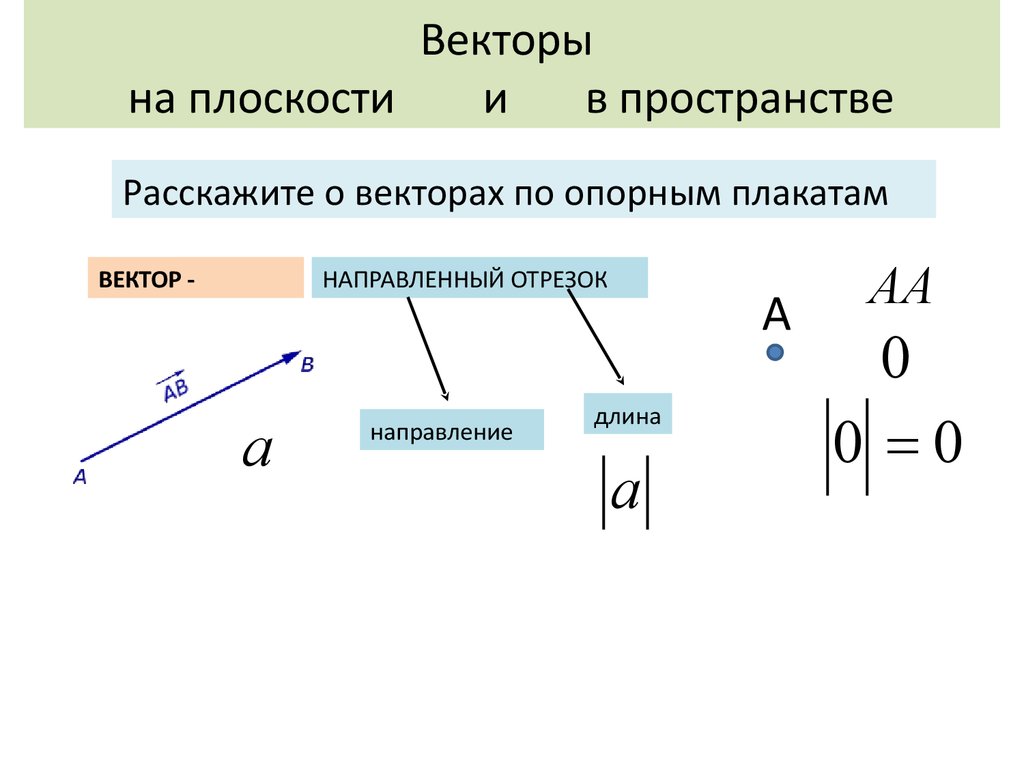
Расскажите о векторах по опорным плакатам
ВЕКТОР -
НАПРАВЛЕННЫЙ ОТРЕЗОК
а
направление
А
длина
а
А А
0
0 0

3.

Векторы
на плоскости
и
в пространстве
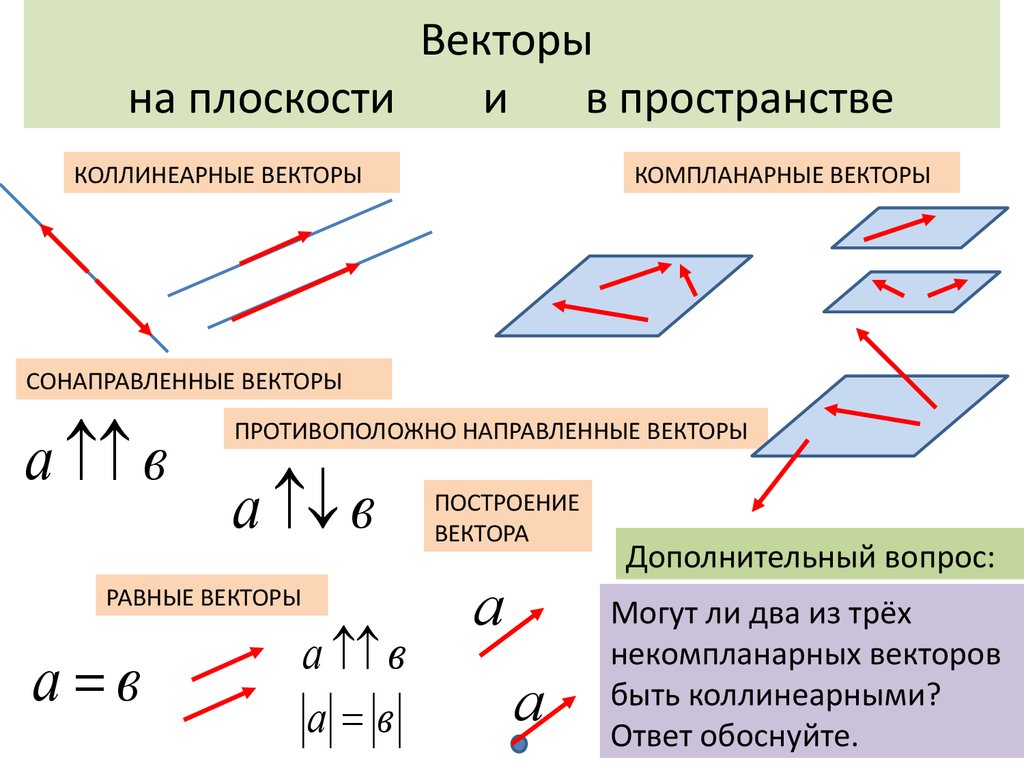
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ
КОМПЛАНАРНЫЕ ВЕКТОРЫ
СОНАПРАВЛЕННЫЕ ВЕКТОРЫ
а в
а в
ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕ ВЕКТОРЫ
РАВНЫЕ ВЕКТОРЫ
а в
а в
а в
ПОСТРОЕНИЕ
ВЕКТОРА
а
а
Дополнительный вопрос:
Могут ли два из трёх
некомпланарных векторов
быть коллинеарными?
Ответ обоснуйте.

4.

Действия
на плоскости
над
и
векторами
в пространстве
а в с
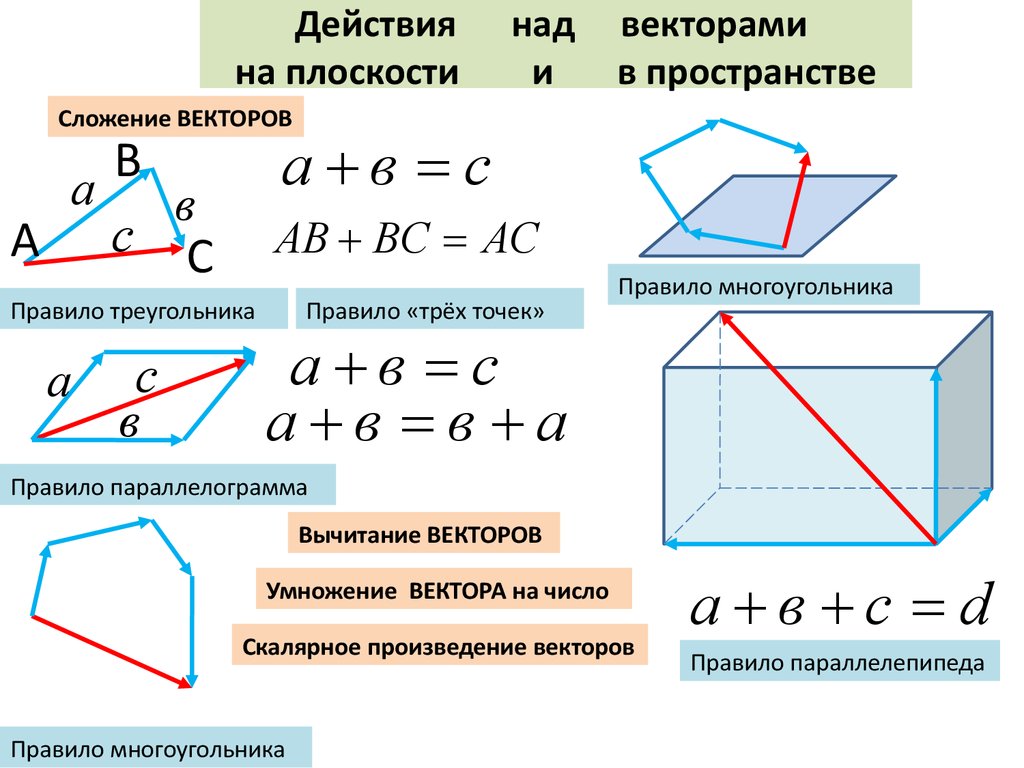
Сложение ВЕКТОРОВ
А
В
а в
АВ ВС АС
с С
Правило треугольника
а с
в
Правило «трёх точек»
а в с
а в в а
Правило многоугольника
Правило параллелограмма
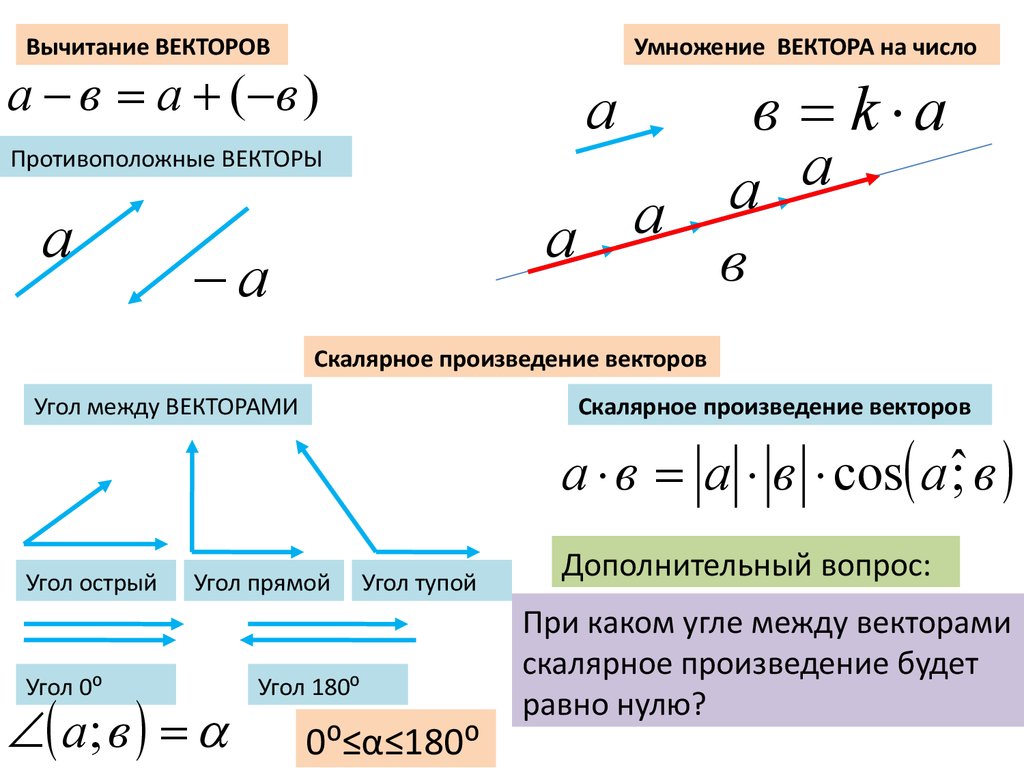
Вычитание ВЕКТОРОВ
Умножение ВЕКТОРА на число
Скалярное произведение векторов
Правило многоугольника
а в с d
Правило параллелепипеда

5.

Вычитание ВЕКТОРОВ
а в а ( в )
в k a
а
а а
а
в
а
Противоположные ВЕКТОРЫ
а
Умножение ВЕКТОРА на число
а
Скалярное произведение векторов
Угол между ВЕКТОРАМИ
Угол острый
Угол 0⁰
Скалярное произведение векторов
а в а в cos a ˆ; в
Угол прямой
а; в
Угол тупой
Угол 180⁰
0⁰≤α≤180⁰
Дополнительный вопрос:
При каком угле между векторами
скалярное произведение будет
равно нулю?

6.

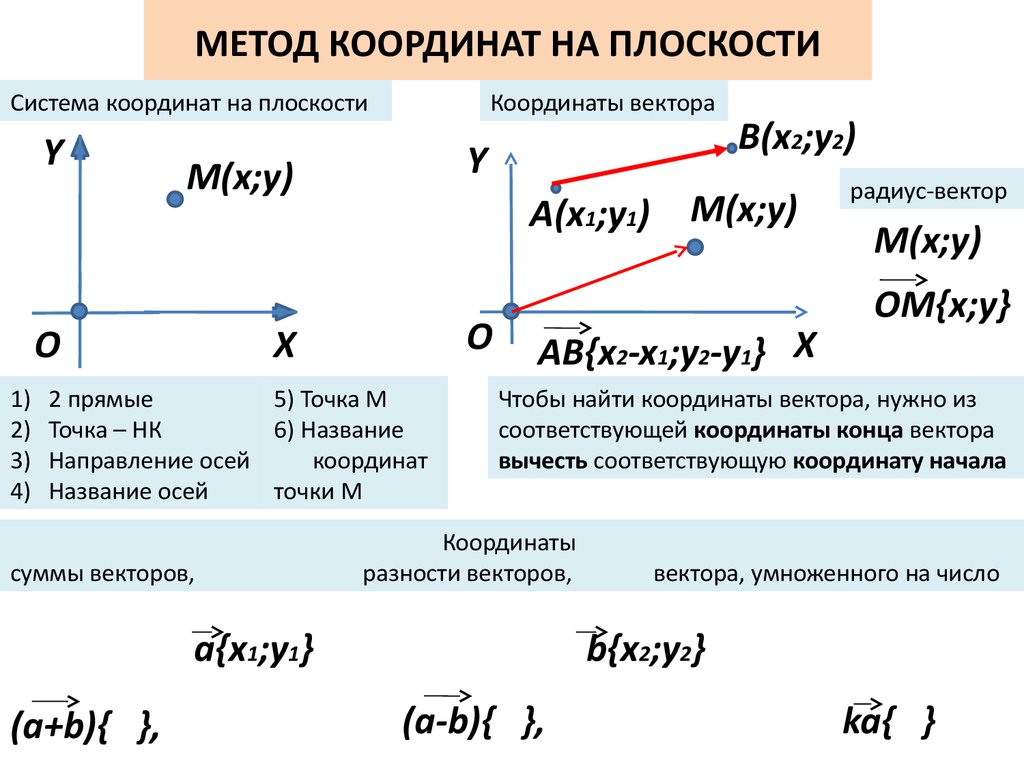
МЕТОД КООРДИНАТ НА ПЛОСКОСТИ
Система координат на плоскости
Y
Y
M(x;y)
О
1)
2)
3)
4)
Координаты вектора
A(x1;y1)
О
X
2 прямые
5) Точка М
Точка – НК
6) Название
Направление осей
координат
Название осей
точки М
суммы векторов,
M(x;y)
AB{x2-x1;y2-y1} X
радиус-вектор
M(x;y)
ОM{x;y}
Чтобы найти координаты вектора, нужно из
соответствующей координаты конца вектора
вычесть соответствующую координату начала
Координаты
разности векторов,
a{x1;y1}
(a+b){ },
B(x2;y2)
вектора, умноженного на число
b{x2;y2}
(a-b){ },
ka{ }

7.

Простейшие задачи в координатах
2) Длина вектора
1) Координаты середины отрезка
C(x;y)
B(x2;y2)
A(x1;y1)
x1 x2
x
,
2
y1 y2
y
2
a{x;y}
2
2
a x y
3) Расстояние между двумя точками
B(x2;y2)
Скалярное произведение в координатах
а в а в cos a ˆ; в
a{x1;y1}
b{x2;y2}
а в x1 x2 y1 y2
A(x1;y1)
AB ( x2 x1 ) 2 ( y2 y1 ) 2

8.

Задание
1 Найдите
вектора
длину
Решение:
{15;
20}.
2
2
a x y
2
2
a 15 20 25
Задание
2 Найдите квадрат длины вектора
.
.
Ответ: 25
Решение:
2
2
2 2
2
2
a ( x y ) x y
AB{12;3}
13
10
AB 12 3 144 9 153
2
6
18
2
2
Ответ: 153

9.

Задание
3 Найдите
вектора
сумму
Решение:
координат
AB{41 8;35 29}
AB{33;6}
35
.
29
4
.
8
Задание
Ответ: 39
41
Векто
с началом в
р
точке
(13; 28) имеет координаты (41;22).
Найдите
абсциссу
точки
Решение: 41=х-13, х=28
Ответ: 28
28
13

10.

5
Задание
Векто
с концом в
27
р (41; 27) имеет
точкекоординаты (27;
19).
Найдите ординату точки
Ответ: 8.
Задание
6 Найдите
вектора
+
Решение:
41
сумму
координат
34
29
а{17;34}, b{42;29} Радиус-векторы
(а в ){17 42;29 34}
(а в ){59;63} Ответ: 122
17
42

11.

Задание
7 Найдите
вектора
квадрат
длины
35
+
Решение:
а{18;35}, b{43;27}
(а в ){61;62}
27
.
18
43
2
a в ( x2 y 2 )2 x2 y 2
2
a в 612 62 2
612 (60 1) 2 3600 120 1 3721
62 2 (60 2) 2 3600 240 4 3844
Ответ: 7565

12.

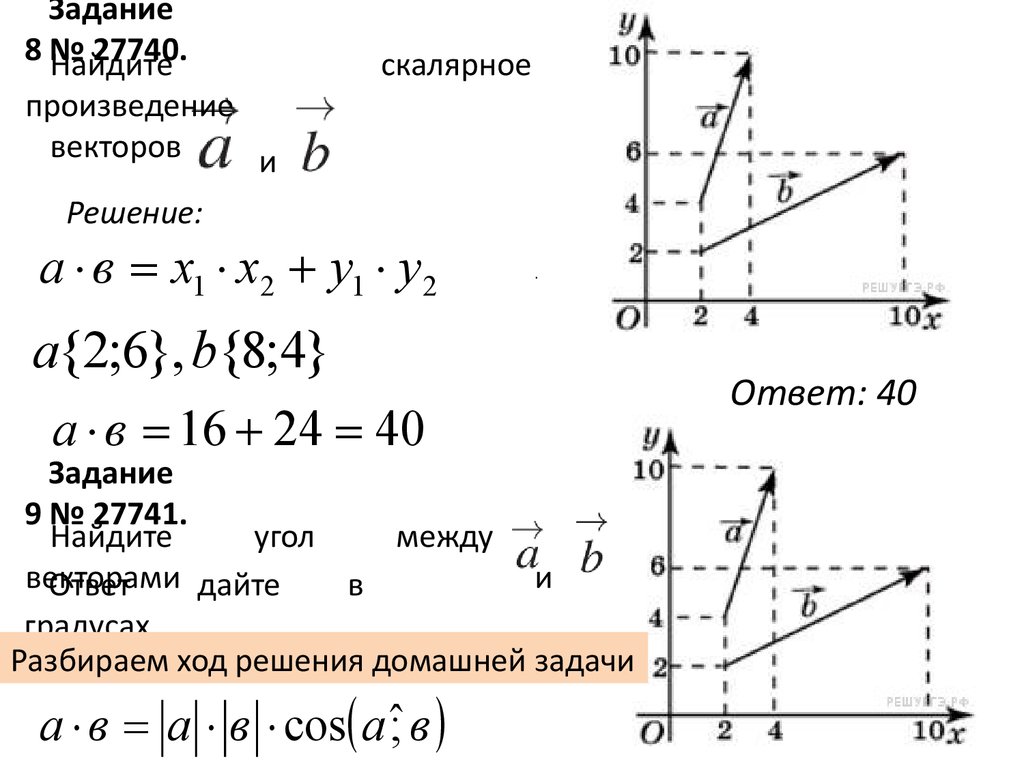
Задание
8№
27740.
Найдите
произведение
векторов
и
скалярное
Решение:
а в x1 x2 y1 y2
а{2;6}, b{8;4}
а в 16 24 40
.
Задание
9 № 27741.
Найдите
угол
между
векторами
и
Ответ
дайте
в
градусах.
Разбираем ход решения домашней задачи
а в а в cos a ˆ; в
Ответ: 40

13.

Домашнее задание с урока 2:
Конспект урока проработать, знать формулы.
Сайт «Решу ЕГЭ» позиция 3:
№ 27663, № 27664,
№ 27723-27732, 27741.