Угол между прямой и плоскостью

1.

2.

BC= 172-152
BC=8
5
В
SinA=
В
tgA=
13
CosA=
15
17
13
5
В
8
С
С
А
?
6
С
CosA= 0,8
10
В
SinA=
4
А
С
А
CA 1
=
14 7
CA= 102-62
В
7
14
С
А
15
1
?
CA=2
2
3
4
BC= 142-22
=
2
BA 3
А
BA=6
BC=8 3

3.

m
A
B
C
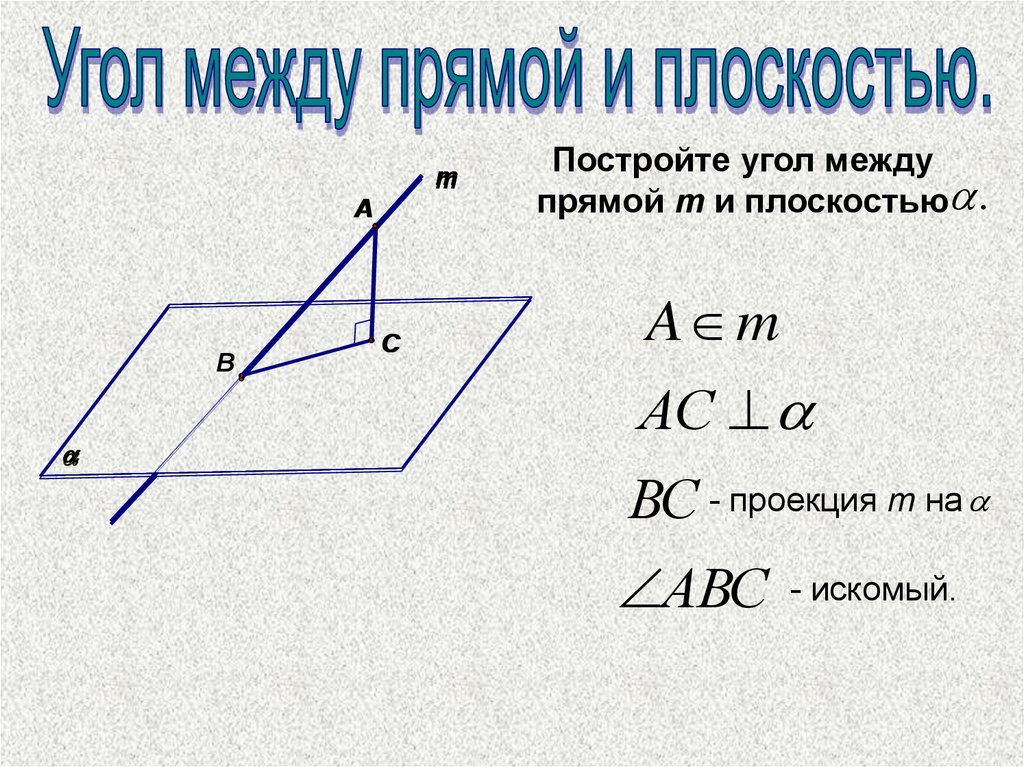
Постройте угол между
прямой m и плоскостью .
A m
АС
ВС - проекция m на
АВС
- искомый.

4.

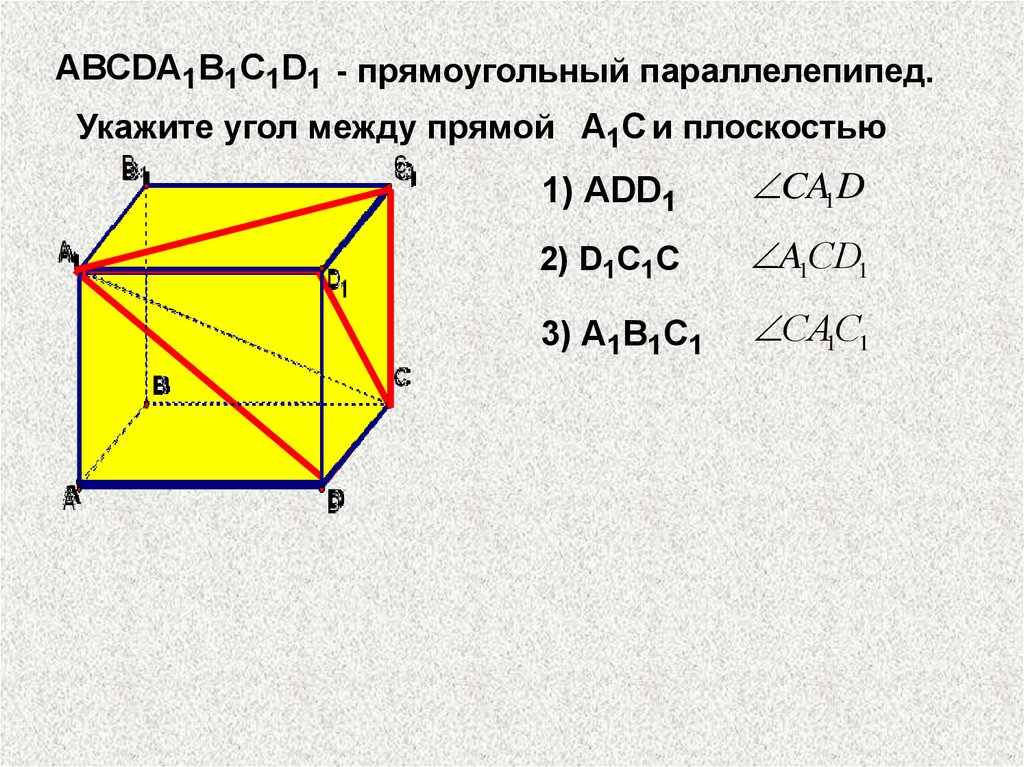
ABCDA1B1C1D1 - прямоугольный параллелепипед.
Укажите угол между прямой A1C и плоскостью
B`1
C1
A1
D1
C
B
A
D
1) ADD1
CA1D
2) D1C1C
A1СD1
3) A1B1C1
СA1С1

5.

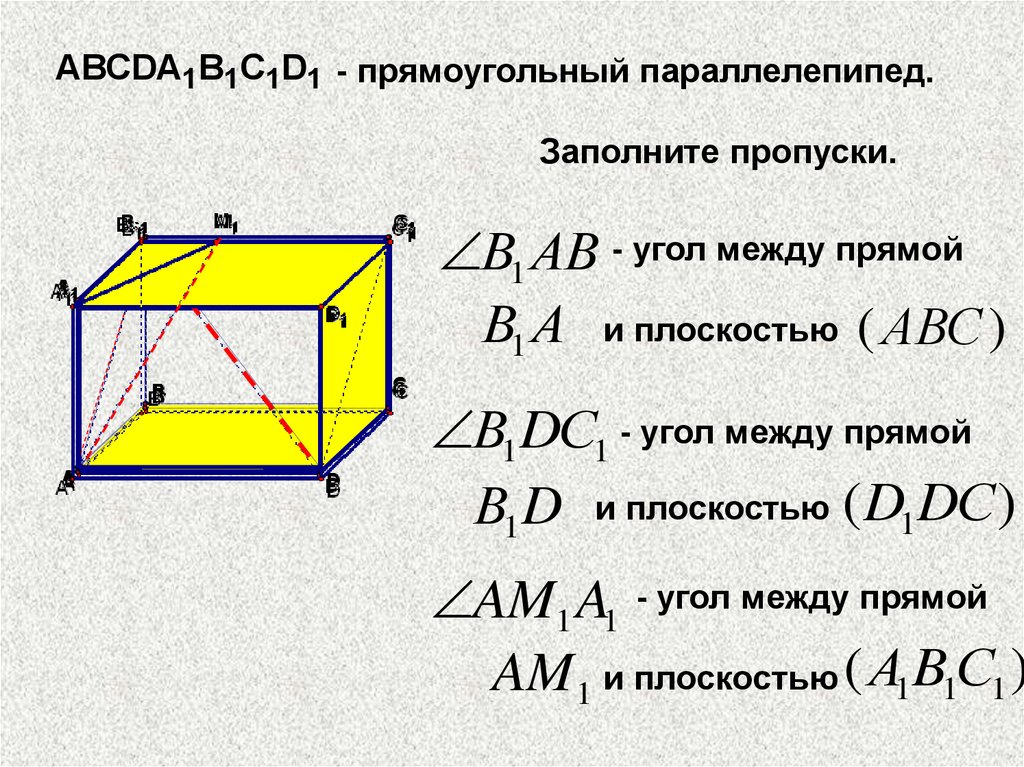
ABCDA1B1C1D1 - прямоугольный параллелепипед.
Заполните пропуски.
M1
B
B`1
`1
A
A11
C
C11
D
D11
C
C
B
B
A
A
D
D
В1 АВ - угол между прямой
В1 А и плоскостью ( АВС )
В1DС1 - угол между прямой
В1 D и плоскостью ( D1DС )
AM1 A1 - угол между прямой
AM1 и плоскостью ( А1B1С1 )

6.

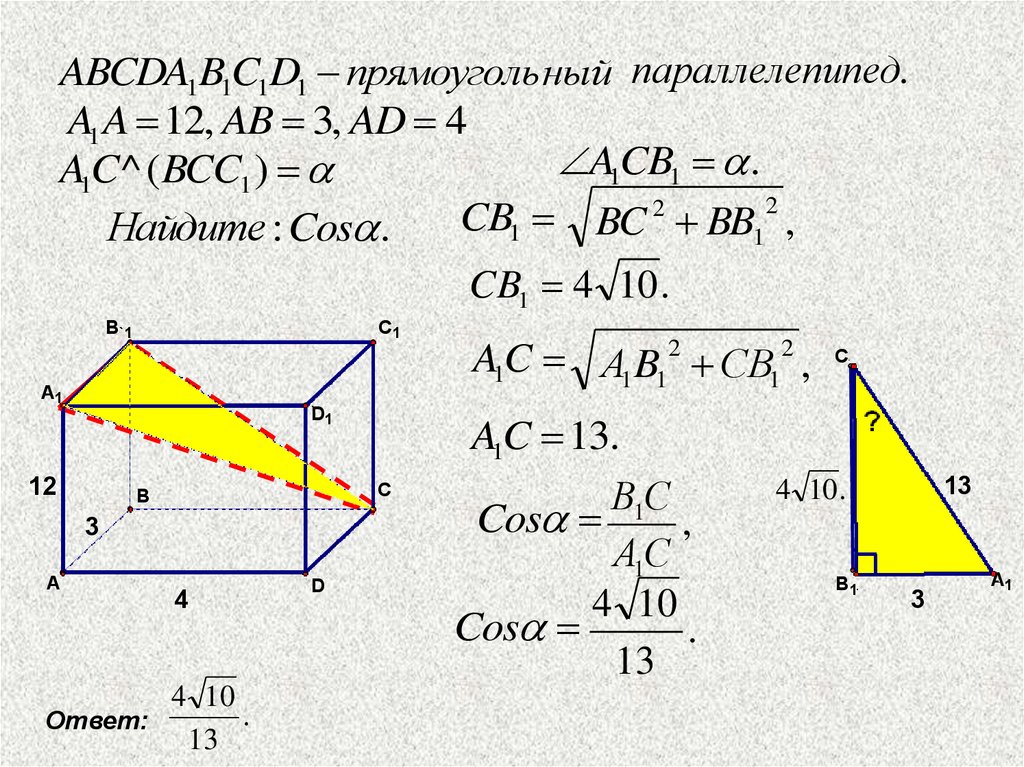
ABCDA1B1C1D1 прямоуголь ный параллелепипед.
A1 A 12, AB 3, AD 4
A1CB1 .
A1C ^ ( BCC1 )
2
2
CB
BC BB1 ,
Найдите : Cos .
1
CB1 4 10 .
B`1
C1
A1
D1
12
C
B
3
A
4
4 10
.
Ответ:
13
D
A1C А1B12 СB12 ,
A1C 13.
В1С
Cos
,
А1С
4 10
Cos
.
13
C
?
13
4 10 .
B1
3
A1

7.

Задача 1
B1
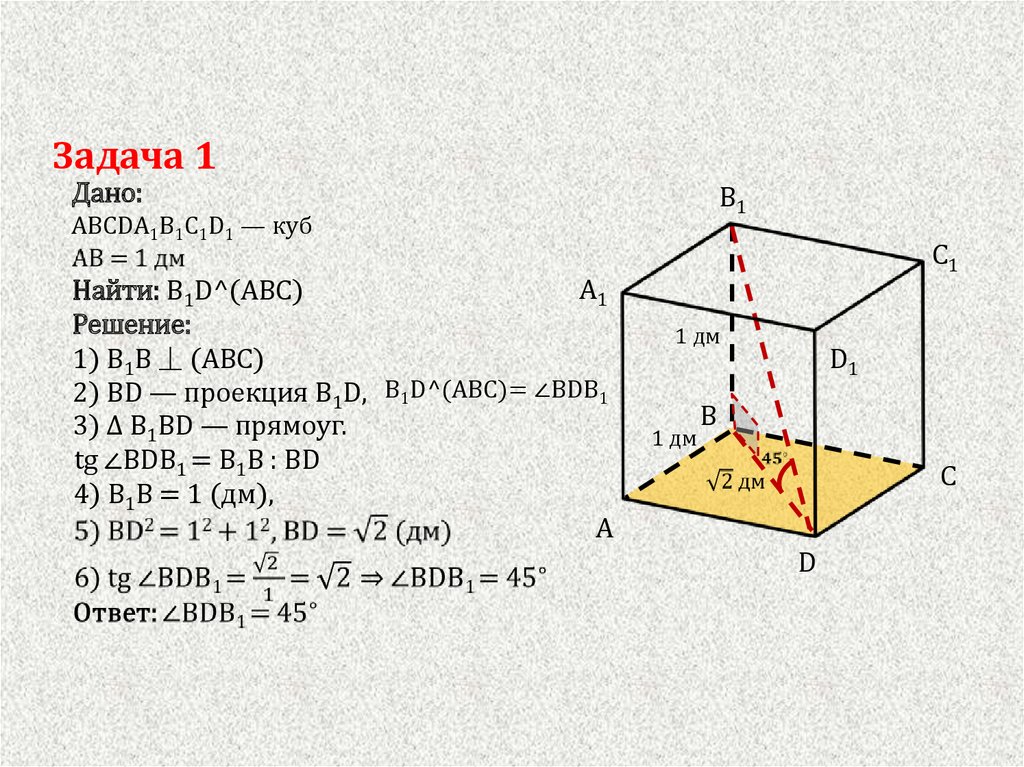
Дано:
ABCDA1B1C1D1 — куб
A1
Найти: B1D^(ABC)
Решение:
1) B1B ⏊ (ABC)
2) BD — проекция B1D, B1D^(ABC)= ∠BDB1
3) ∆ B1BD — прямоуг.
tg ∠BDB1 = B1B : BD
4) B1B = 1 (дм),
A
C1
1 дм
1 дм
D1
B
C
D

8.

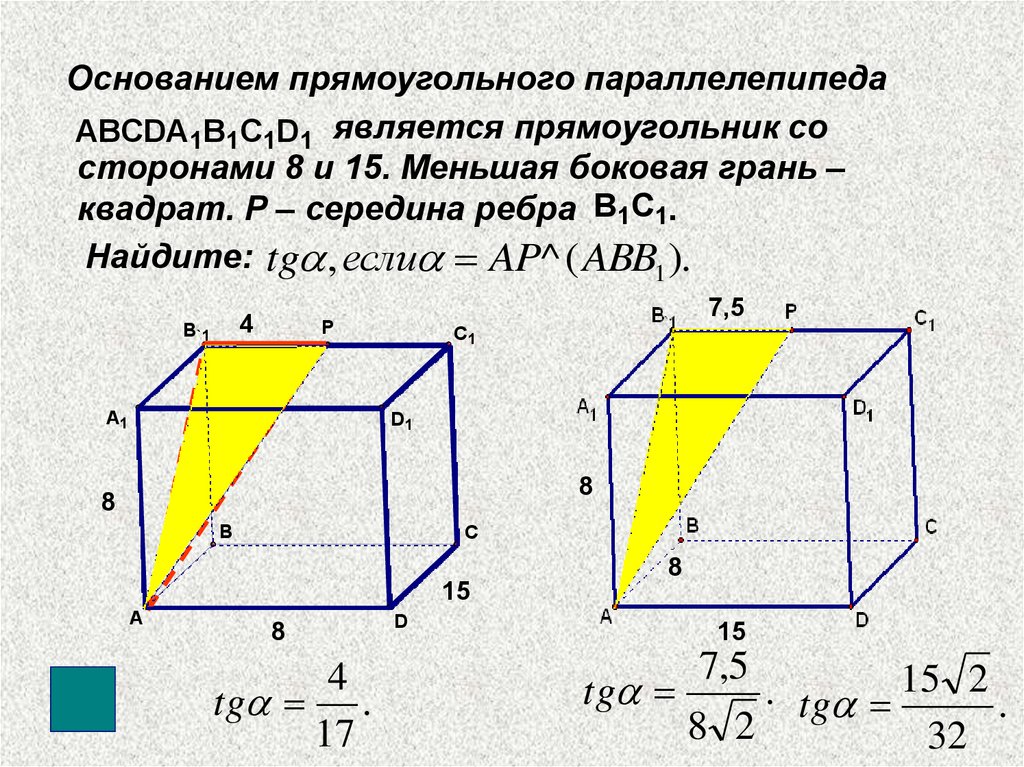
Основанием прямоугольного параллелепипеда
ABCDA1B1C1D1 является прямоугольник со
сторонами 8 и 15. Меньшая боковая грань –
квадрат. Р – середина ребра B1C1.
Найдите: tg , если AP^ ( ABB1 ).
4
B`1
7,5
P
A1
C1
D1
8
8
B
C
8
15
A
8
4
tg .
17
D
15
7,5
tg
. tg 15 2 .
8 2
32