Угол между плоскостями. (Урок 3. Решаем С2 ЕГЭ. 11класс)

1.

Тема: Угол между плоскостями. Урок 3
«Решаем С2 ЕГЭ»
Разработала: Куракова Е. В., учитель математики
МБОУ СОШ с УИОП №38
им.Е.А. Болховитинова
11 класс физико-математического профиля

2.

Цели:
Повторить понятие угла между
плоскостями, нормали к плоскости.
Закрепить методы введение координат
Рассмотреть примеры С2 ЕГЭ
Блитц-опрос по терминам

3.

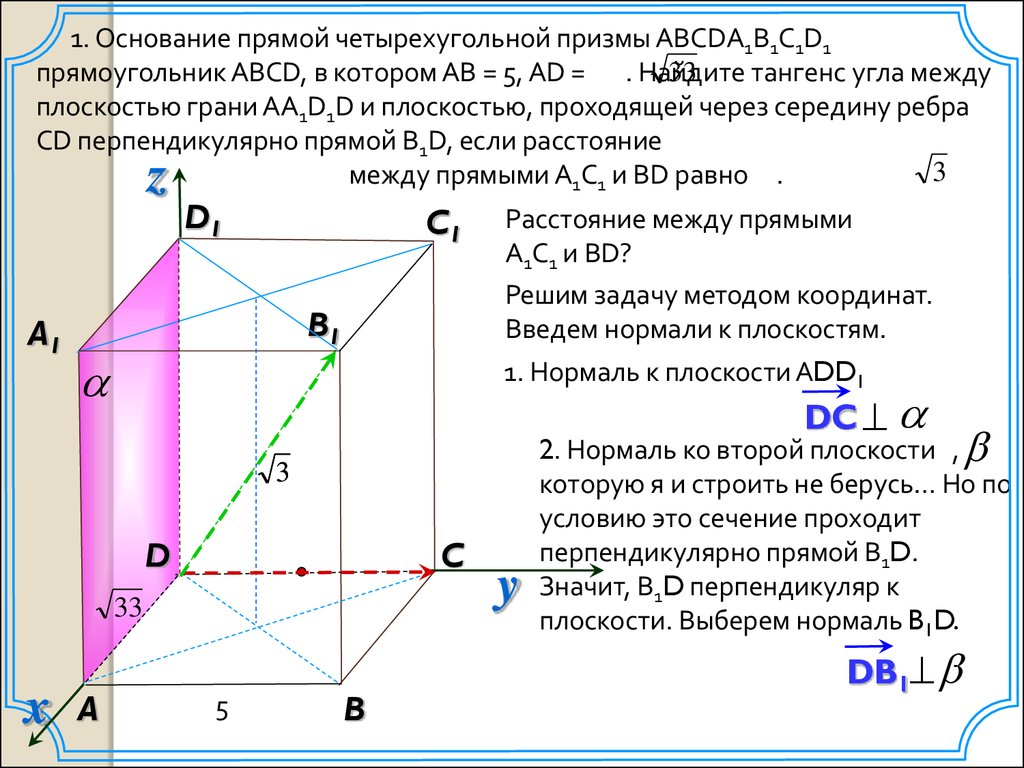
1. Основание прямой четырехугольной призмы ABCDA1B1C1D1
прямоугольник ABCD, в котором AB = 5, AD = . Найдите
тангенс угла между
33
плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра
CD перпендикулярно прямой B1D, если расстояние
3
между прямыми A1C1 и BD равно .
z
A1
D1
C1
B1
Расстояние между прямыми
A1C1 и BD?
Решим задачу методом координат.
Введем нормали к плоскостям.
1. Нормаль к плоскости АDD1
DC
3
D
C
33
x
A
5
B
y
2. Нормаль ко второй плоскости ,
которую я и строить не берусь… Но по
условию это сечение проходит
перпендикулярно прямой В1D.
Значит, В1D перпендикуляр к
плоскости. Выберем нормаль B1D.
DB1

4.

Основание прямой четырехугольной призмы ABCDA1B1C1D1
прямоугольник ABCD, в котором AB = 5, AD = . Найдите
тангенс угла между
33
плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра
CD перпендикулярно прямой B1D, если расстояние
3
между прямыми A1C1 и BD равно .
z
A1
D1
C1
B1 ( 33; 5; )3
3
Я выбрала очень удобно нормальные
векторы. Ведь это радиус-векторы.
Координаты радиус-вектора такие
же, как и координаты конца вектора.
Значит, нам надо найти координаты
точек В1 и С.
1. DB1
3
D
C (0; 5; 0)
y
33
x
A
5
B
2. DC

5.

DC (0; 5; 0)
DB1 ( 33; 5; )3
3. cos
Теперь найдем тангенс.
2
tg A 1
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22
tg 1
1
2
cos
33 0 5 5 3 0
33 5 3
2
2
2
0 2 52 0 2
5
61
2
61
tg 1
25
2
0 25 0
25
5
.
61
5
61
33 25 3 25
cos
1
cos2 A
5
61
tg 2
61
1
25
36
tg
25
2
tg
т.к.
6
5
6
tg
5
– острый угол

6.

2. В прямоугольном параллелепипеде ABCDA1B1C1D1
AB = 3, ВС = 4, АА1 = 12. Через середину ребра АВ перпендикулярно
диагонали ВD1 проведена плоскость. Найдите угол образованный этой
плоскостью с основанием параллелепипеда.
Решим задачу методом координат.
D1 (0; 0; 12)
C1 Введем нормали к плоскостям.
1. Нормаль к плоскости АBC
z
DD
A1
2. Нормаль ко второй плоскости ,
1
которую я и строить не берусь… Но по
условию это сечение проходит
перпендикулярно прямой BD1.
Значит, ВD1 - перпендикуляр к
плоскости. Выберем нормаль D1B.
B1
12
C
D
x
A
3
4
B (4; 3; 0)
y
DD (0;0;12)
D1B
D1B ( 4; 3;-12)
1DD1 –найти
это радиус-вектор,
поэтому
Чтобы
координаты вектора
D1его
B,
координаты
такие
же, как
и начало.
точки D1
вычтем
из конца
вектора
его

7.

DD (0;0;12)
D1B ( 4; 3;-12)
1
cos
cos
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22
0 4 0 3 12 12
0 2 0 2 12 2 4 2 32 12
2
144
12 169
12
12
144
13
12 13
12
cos
13
12
Ответ : arc cos
13

8.

3. Основание прямой четырехугольной призмы ABCDA1B1C1D1
прямоугольник ABCD, в котором AB = 12, AD = 31. Найдите косинус угла
между плоскостью основания и плоскостью, проходящей через середину
ребра A1D1 перпендикулярно прямой BD1, если расстояние
между прямыми AC и B1D1 равно 5.
z
D1
C1
A1
B1
Расстояние между прямыми AC и
B1D1?
Решим задачу методом координат.
Введем нормали к плоскостям.
1. Нормаль к плоскости АBC
DD
5
C
D
y
31
x
A
12
B
2. Нормаль ко второй плоскости ,
1
которую я и строить не берусь… Но по
условию это сечение проходит
перпендикулярно прямой BD1.
Значит, ВD1 - перпендикуляр к
плоскости. Выберем нормаль D1B.
D1B

9.

z
D1 (0; 0; 5)
C1
DD1 – это радиус-вектор, поэтому его
координаты такие же, как и точки D1
DD (0; 0; 5)
1
A1
B1
Чтобы найти координаты вектора D1B,
5 вычтем из конца вектора его начало.
D1B ( 31; 12; -5)
C
D
y
31
x
A
12
B ( 31; 12; 0)

10.

DD (0; 0; 5)
D1B ( 31; 12; -5)
1
cos
cos
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22
0 31 0 12 5 5
0 2 0 2 52
31 12
2
2
5
2
0 0 25
25 31 144 25
25
2
5
1 2
5
5 200
4
10 2 2 2 2
2 100
Ответ : cos
2
4

11.

4. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра:, AB
= 5,
угол между плоскостями CD1B1и AD1B1 .
12 x= 12,
0 yСС
15=z 5.
Найдите
0
AD
В данной
задаче
построение линейного угла не столь очевидно.
0
x
5
y
5
z
0
z
Поэтому применим метод координат.
Выразим через
х переменные y и Найдем
z
D1(0;0;5)
вектор нормали плоскости AD1B1.
C1
Из (1): 5z 12 x Рассмотрим два вектора этой плоскости:
12 x 5 z 0
«–»
5 y 5z 0
AD1(-12;0;5)
AB1 (0;5;5)
12
A1 12 x 5 y5 0B1 (12;5;5) z 5 x
Пусть вектор нормали n {x;y;z}.
Вектор, перпендикулярный
5 y 12 x
плоскости, будет перпендикулярен
12
y D x
5
C (0;5;0) любой прямой, лежащей в этой
5
плоскости. Тогда,
Эта система имеет бесконечное
AD1 n значит, AD1 n = 0
множество решений, так как
векторов, 5
перпендикулярных плоскости
AB1 n значит, AB1 n = 0
A
(12;0;0)
AD1B1, бесконечно B
х
много. Выберем из данного множества
ненулевой вектор n,
положив х = 1,
12
тогда у = – , z = 12
5
5
ВекторПолучим
нормалисистему
плоскости AD1B1:
n (1;– 12; 12)
5
5

12.

0 x 5 y 5z 0
12 x 0 y z5 z 0
D (0;0;5)
Выразим через 1х переменные Cy1 и zНайдем вектор нормали плоскости CD1B1.
Рассмотрим два вектора этой плоскости:
Из (2): 5 z 12 x
5 у 5 z 0
CD1(0;-5;5)
CB1 (12;0;5)
«–»
A1 12 х 5 z 50 B1 (12;5;5)z 12 x
Пусть вектор нормали s {x;y;z}.
5 y 12 x 0
5
Вектор, перпендикулярный
5 y 12 x
плоскости, будет перпендикулярен
12
5
C (0;5;0) любой прямой, лежащей в этой
y D x
плоскости. Тогда,
5
Эта система имеет бесконечное
CD1 s значит, CD1 s = 0
множество5решений, так как
векторов,
перпендикулярных плоскости
A (12;0;0)
хCD1B1, бесконечно B
много. Выберем из данного множества
ненулевой вектор s,
положив х = 1,
12
тогда у = – 12, z = –
5
5
CB1 s
значит,
CB s = 0
1
систему
ВекторПолучим
нормали
плоскости CD1B1:
s (1;– 12;– 12)
5
5

13.

n (1;– 12; 12)
5
cos
5
5
cos
5
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22
12 12 12 12
1 1
5 5 5 5
2
2
2
12 12
12 12
2
2
1 1
5 5
5 5
1
cos
1
cos
s (1;– 12;– 12)
144 144
25 25
144 144
144 144
1
25 25
25 25
1
313 313
25
25
313
cos 1 :
25
cos
25
313
arccos
25
313
2

14.

7. В правильной четырехугольной призме ABCDA1B1C1D1 диагональ
основания в 2 раза больше бокового ребра. Найдите угол между плоскостью
АCB
12иxбоковой
2 y 0гранью
z 0 ВВ1С1С.
В
линейного угла не столь очевидно. Поэтому
данной
0 x задаче
2 y z построение
0
применим метод координат.
Если в задаче не дано числовое
Выразим через х переменные y и z
Вектор нормали плоскости ВВ1С1:
значение, то можем обозначить
у x вектор
боковое
реброплоскости
«1», тогда диагональ
нормали
АCB1.
2 x 2 уz 0 / : 2 Из (1)Найдем
основания
равна
2. Найдем
сторону
Рассмотрим
два
вектора
этой
плоскости:
2 y z 0 D1
основания. Основание – квадрат.
C1
D (- 2 ; 2;0)С
2;1)
AC
AB1 (0; CD
2x z 0
sin 450
z1 2 x
Пусть вектор
2 нормали n {x;y;z}. 2
?
A1
B1 ( 2 ; 2;1)
Вектор, перпендикулярный
2 CD
Эта система имеет бесконечное
0
плоскости,
45 будет перпендикулярен
А
множество решений, так как
2 в этой
2
В
любой прямой, лежащей
векторов, перпендикулярных плоскости
плоскости. Тогда,
CD 2
2
D
C (0; 2;0)
ACB1, бесконечно
pданного
(0; 2;0)множества
AC n значит, AC n = 0
много. Выберем
из
2
ненулевой вектор n,
положив х = 1,
у x
zA ( 2;0;0)
2 x тогда у B= 1, z = –
х
AB1 n значит,
2
AB n = 0
1
Получимплоскости
систему ACB1:
Вектор нормали
n (1;1;- 2)

15.

p (0; 2;0)
0
2
1
cos
2
600
1 1 2
0 1 2 1 0 2
cos
cos
cos
n (1;1;- 2)
2 0
2
2 4
2
2
2
2
2
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22

16. Домашнее задание

1. Основание прямой четырехугольной призмы ABCDA1B1C1D1
прямоугольник ABCD, в котором AB = 5, AD = . Найдите тангенс угла
между плоскостью ВA1D1 и плоскостью, проходящей через середину
ребра CD перпендикулярно прямой B1D, если расстояние между
прямыми A1C1 и BD равно .
2. В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = 3, ВС = 4,
АА1 = 12. Через середину ребра АВ перпендикулярно диагонали ВD1
проведена плоскость. Найдите угол образованный этой плоскостью
боковыми плоскостями параллелепипеда.
3. Основание прямой четырехугольной призмы ABCDA1B1C1D1
прямоугольник ABCD, в котором AB = 12, AD = . Найдите косинус угла
между плоскостью основания и плоскостью, проходящей через
середину ребра A1D1 перпендикулярно прямой B1D, если расстояние
между прямыми AC и B1D1 равно 5.
4. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра:
AB = 5, AD = 12, СС1 = 5. Найдите угол между плоскостями CD1B1и
AD1B1.
5. В правильной четырехугольной призме ABCDA1B1C1D1 диагональ
основания в 2 раза больше бокового ребра. Найдите угол между
плоскостью DCB1и боковой гранью ВВ1С1С.