Теорема про три перпендикуляр

1.

Теорема
про три
перпендикуляри

2.

1.Сформулюйте означення прямої перпендикулярної
до площини
2. Сформулюйте і поясніть ознаку
перпендикулярності прямої і плошини
3. Сформулюйте властивість прямих
перпендикулярних до площини
4. Сформулюйте властивість медіани
рівнобедреного трикутника, проведеної до основи
5. Назвіть залежність, яка існує між похилими,
проведеними з однієї точки, та їх проекціями

3.

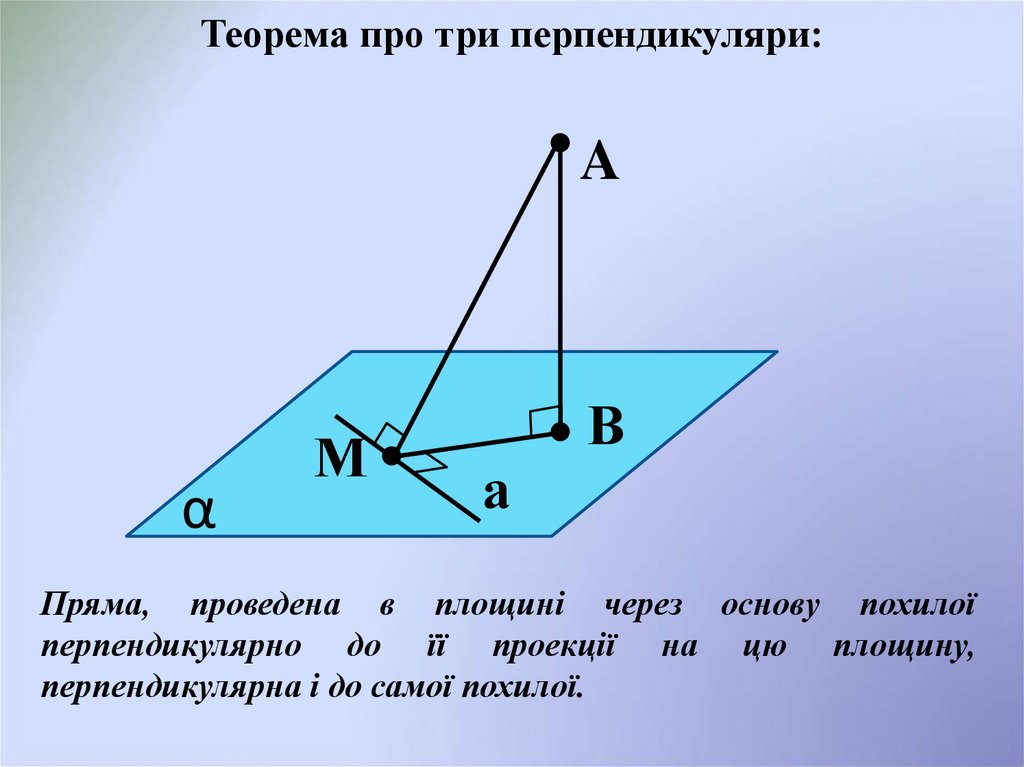
Теорема про три перпендикуляри:
A
α
М
В
а
Пряма, проведена в площині через основу похилої
перпендикулярно до її проекції на цю площину,
перпендикулярна і до самої похилої.

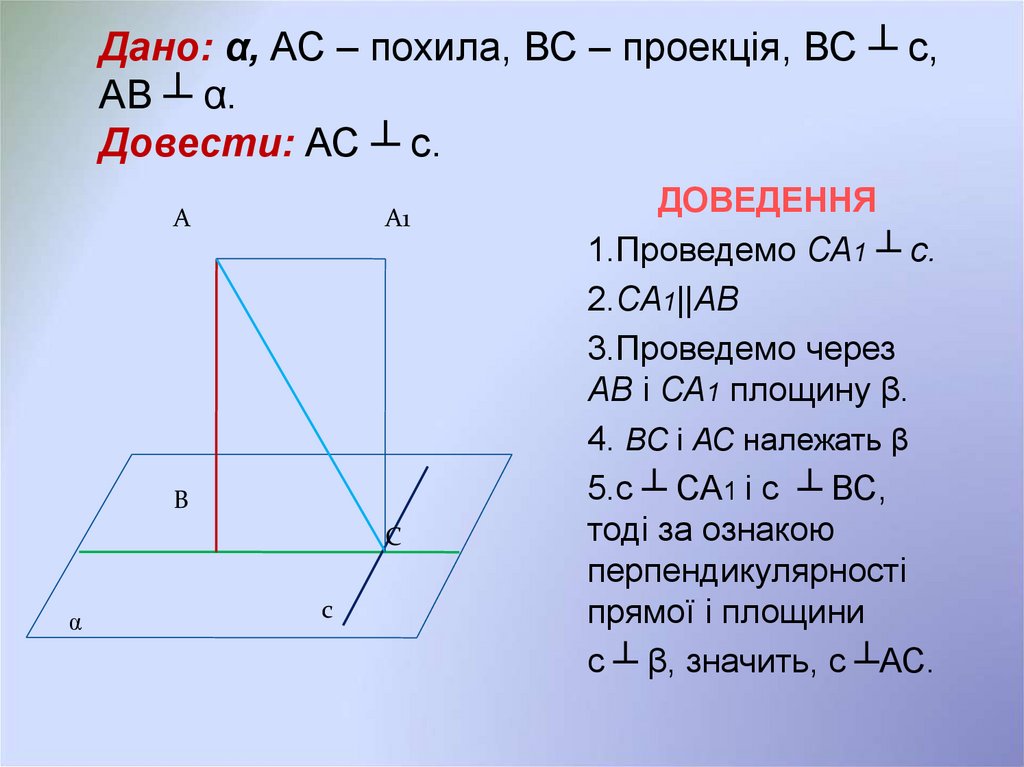
4. Дано: α, АС – похила, ВС – проекція, ВС ┴ с, АВ ┴ α. Довести: АС ┴ с.

А
А1
В
С
α
с
ДОВЕДЕННЯ
1.Проведемо СА1 ┴ с.
2.СА1||АВ
3.Проведемо через
АВ і СА1 площину β.
4. ВС і АС належать β
5.с ┴ СА1 і с ┴ ВС,
тоді за ознакою
перпендикулярності
прямої і площини
с ┴ β, значить, с ┴АС.

5.

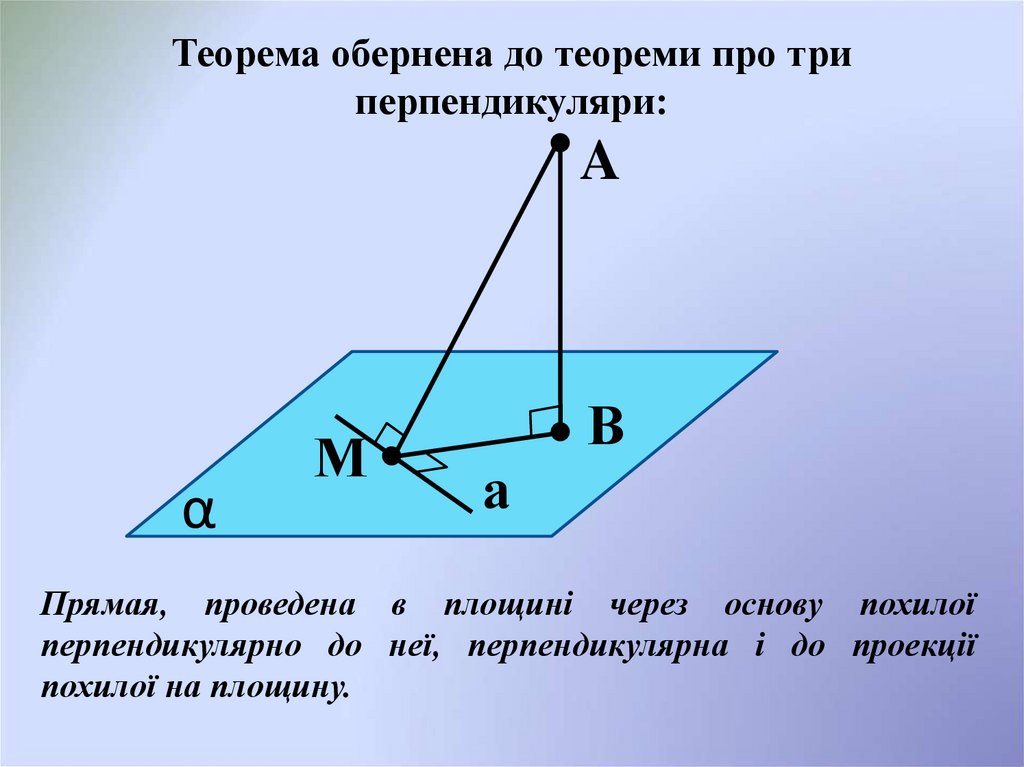
Теорема обернена до теореми про три
перпендикуляри:
A
α
М
В
а
Прямая, проведена в площині через основу похилої
перпендикулярно до неї, перпендикулярна і до проекції
похилої на площину.

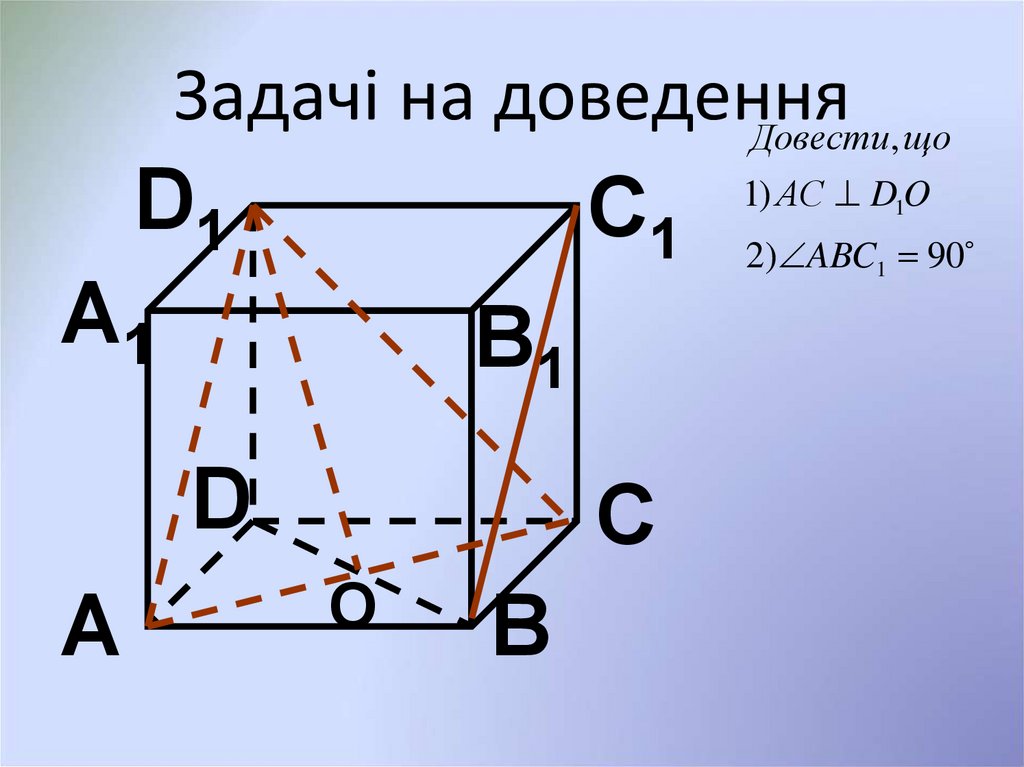
6. Задачі на доведення

Довести, що
D1
C1
A1
B1
D
A
C
O
B
1) АС D1O
2) ABC1 90

7.

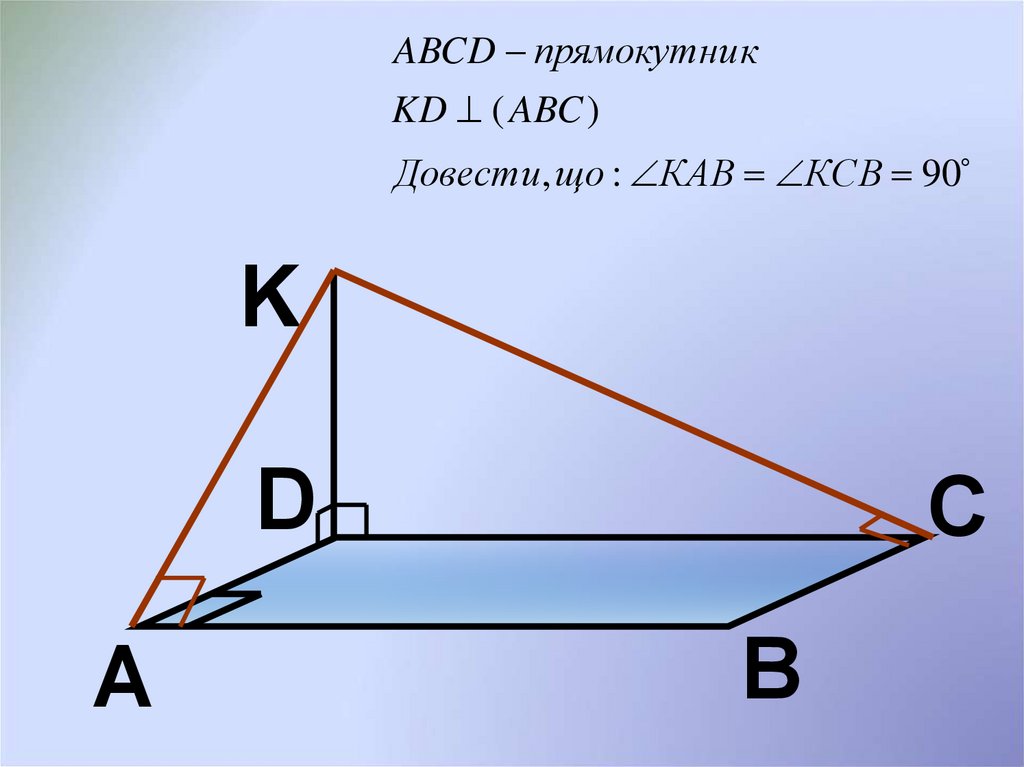
ABCD прямокутни к
KD ( ABC )
Довести , що : КАВ КСВ 90
K
D
A
C
B

8.

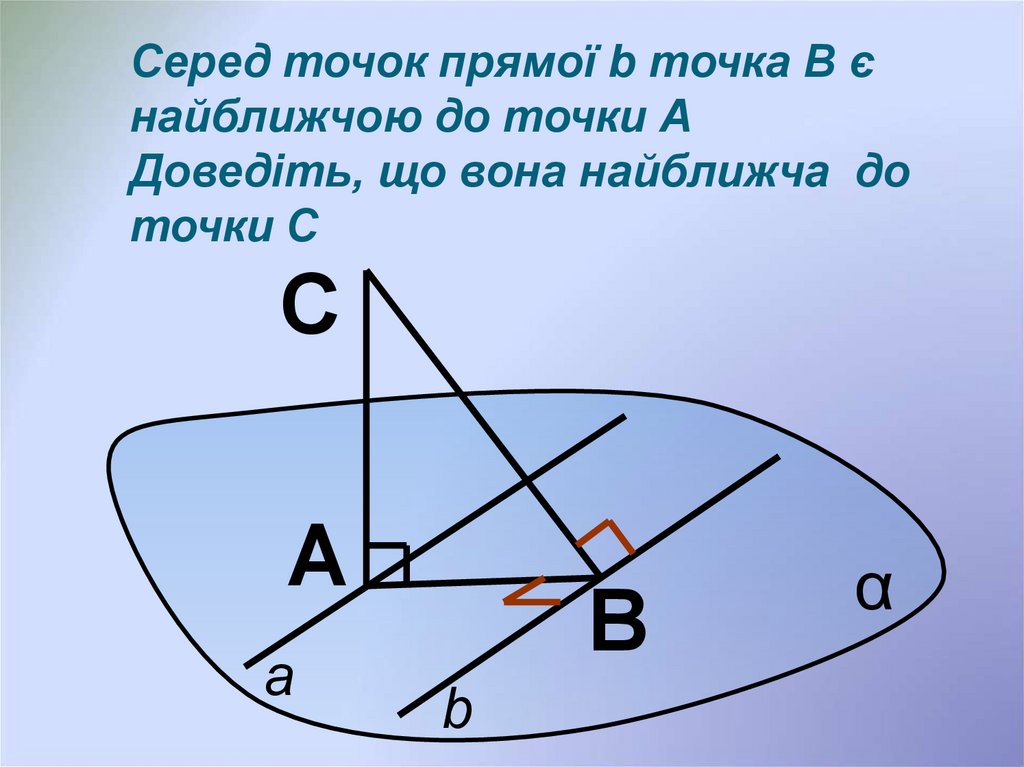
Серед точок прямої b точка В є
найближчою до точки А
Доведіть, що вона найближча до
точки С
C
A
a
B
b
α

9.

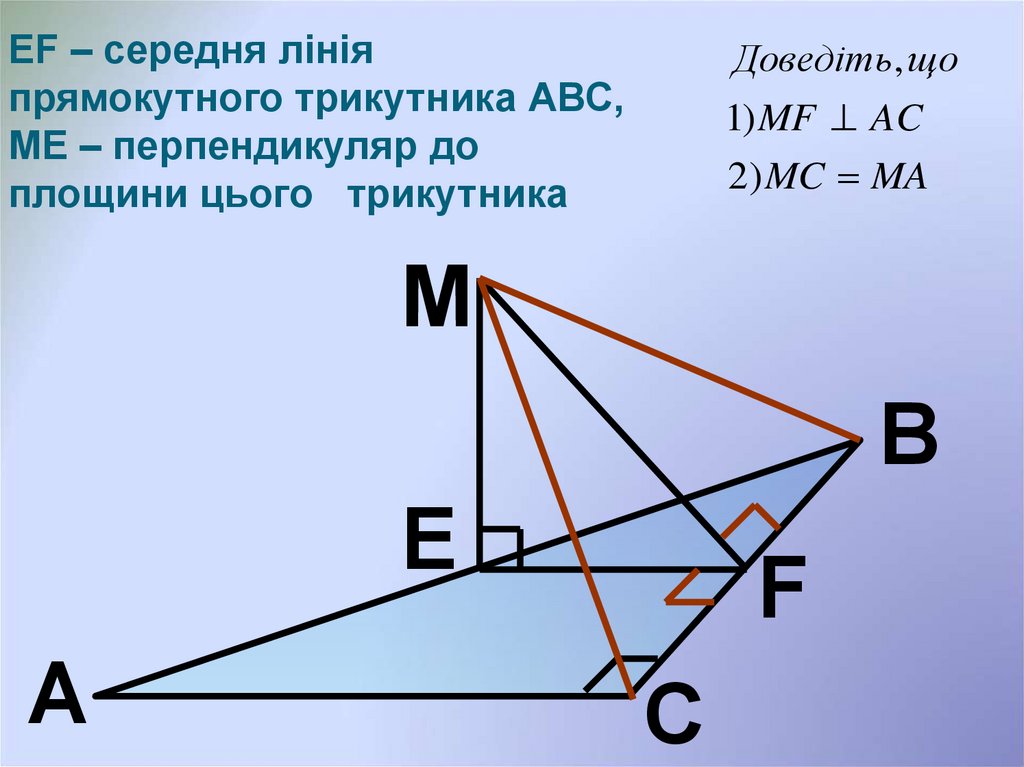
EF – середня лінія
прямокутного трикутника АВС,
МЕ – перпендикуляр до
площини цього трикутника
Доведіть, що
1) MF AC
2) MC MA
M
B
E
A
F
C

10.

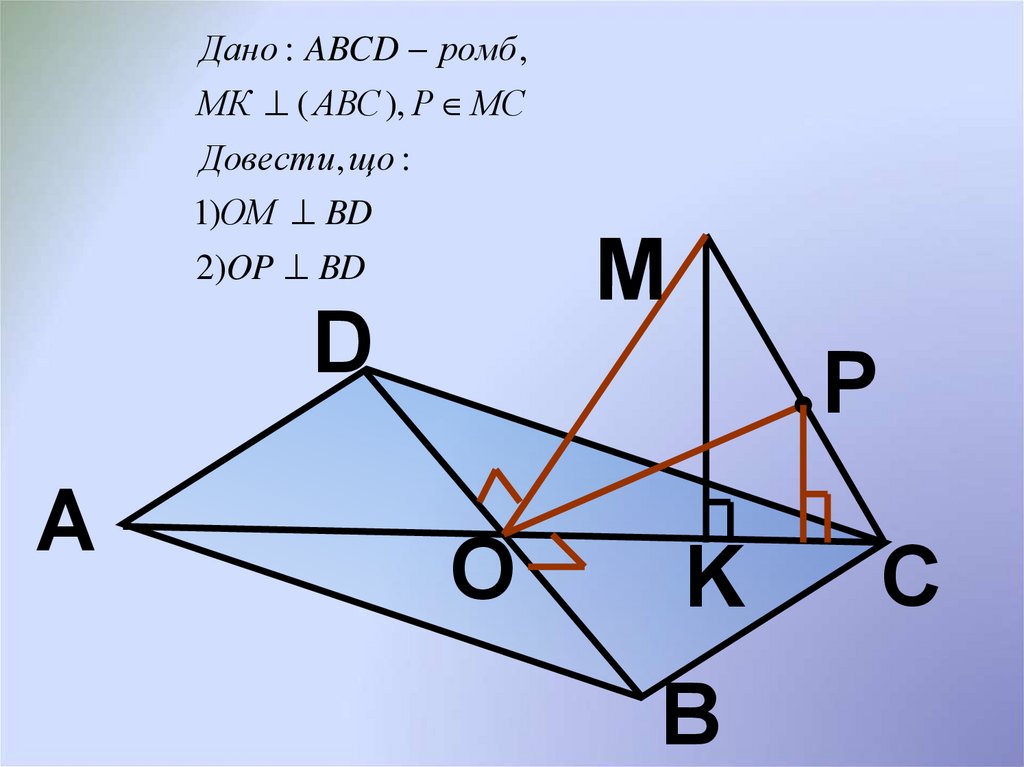
Дано : ABCD ромб ,
МК ( АВС ), Р МС
Довести , що :
1)ОМ BD
M
2)OP BD
D
A
P
O
K
B
C

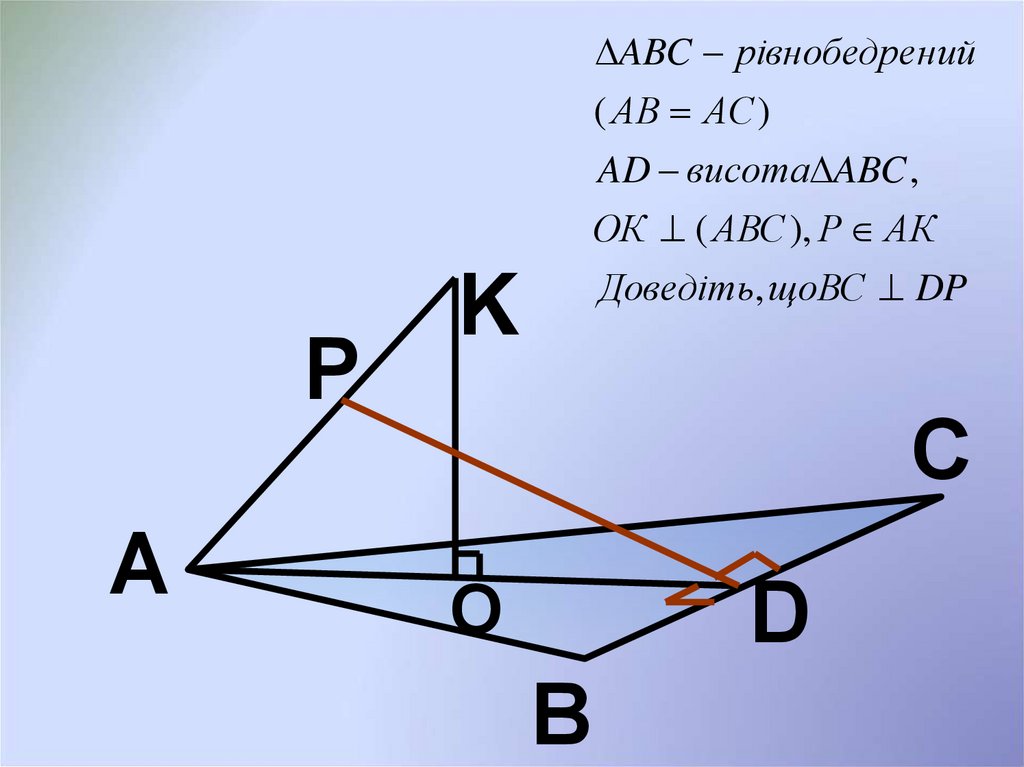
11.

ABC рівнобедре ний
( АВ АС )
AD висота ABC ,
ОК ( АВС ), Р АК
P
Доведіть, щоBC DP
K
C
A
D
O
B

12. Задачі на побудову

• Відрізок МС перпендикулярний площині
рівностороннього трикутника АВС.
• Проведіть через точку М перпендикуляр
до прямої АВ
М
С
А
B

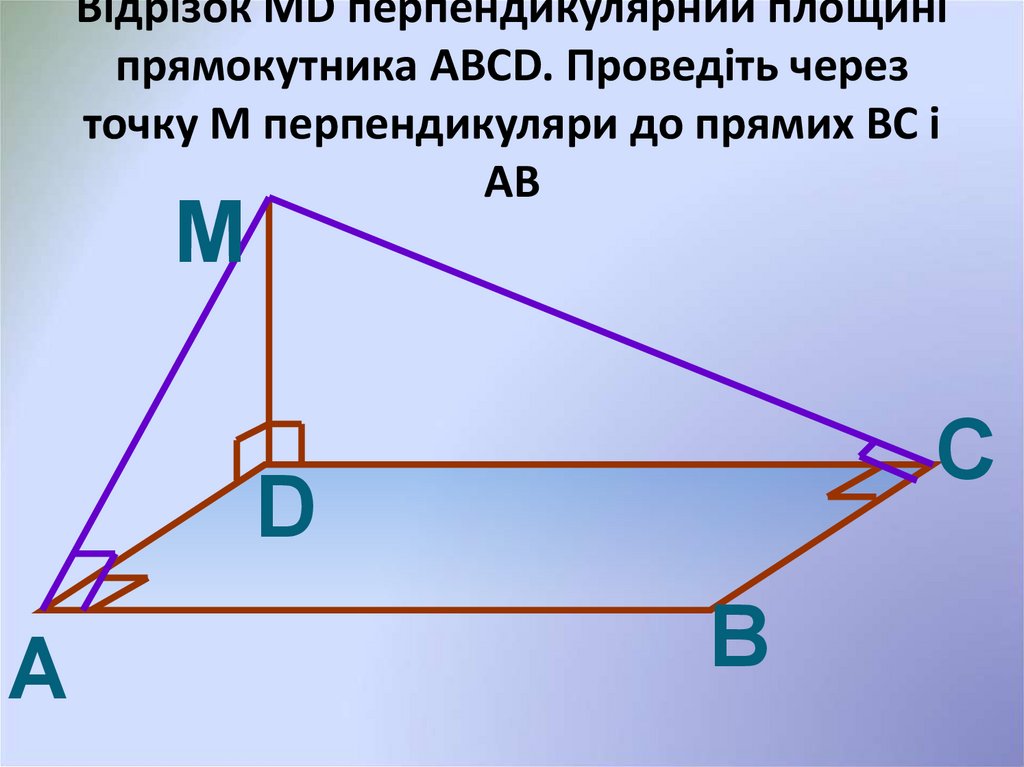
13. Відрізок MD перпендикулярний площині прямокутника ABCD. Проведіть через точку М перпендикуляри до прямих ВС і АВ

M
C
D
A
B

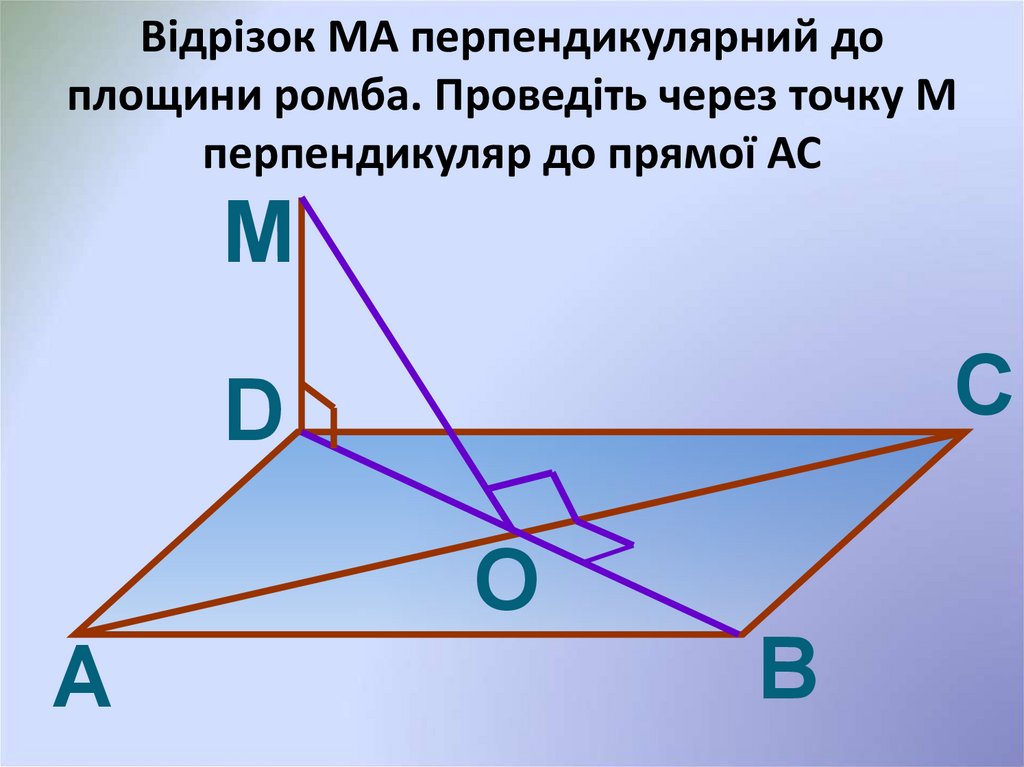
14. Відрізок МА перпендикулярний до площини ромба. Проведіть через точку М перпендикуляр до прямої AC

M
C
D
O
A
B

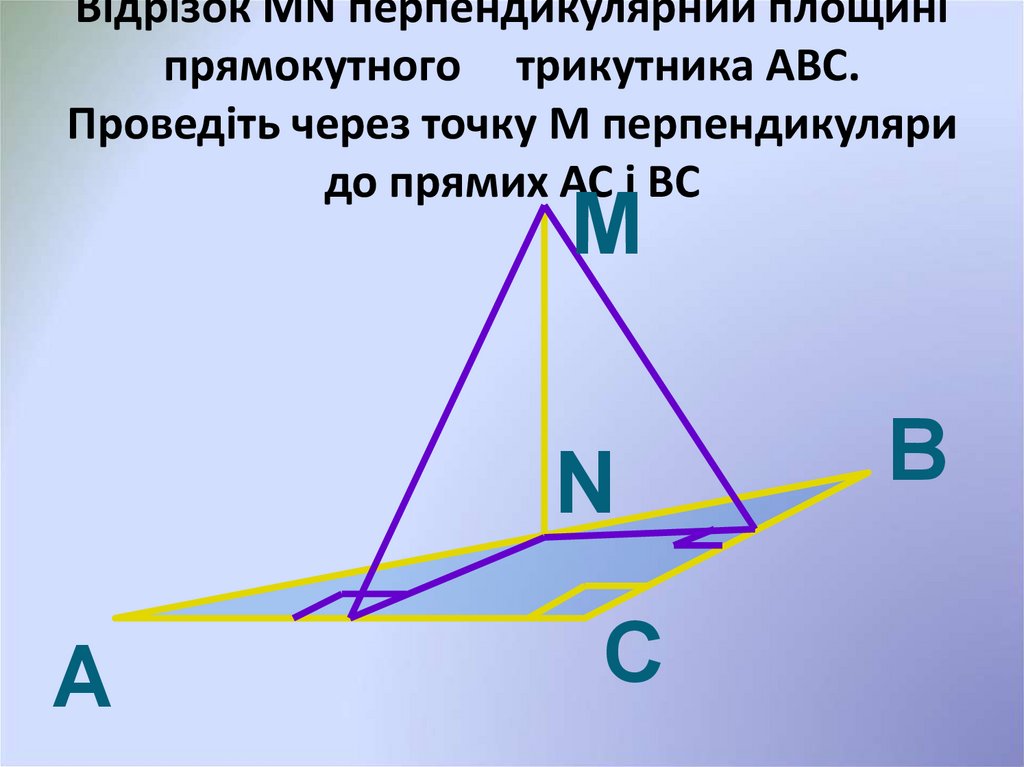
15. Відрізок MN перпендикулярний площині прямокутного трикутника АВС. Проведіть через точку М перпендикуляри до прямих АС і ВС

M
N
A
C
B

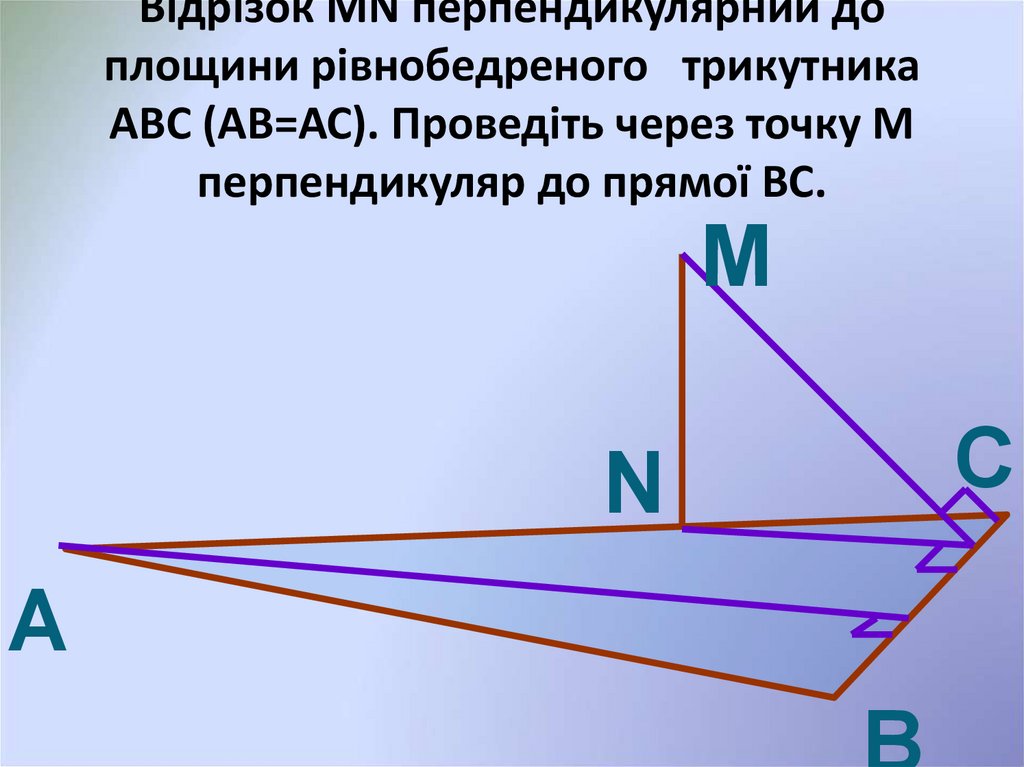
16. Відрізок MN перпендикулярний до площини рівнобедреного трикутника АВС (АВ=АС). Проведіть через точку М перпендикуляр до прямої

ВС.
М
N
A
С

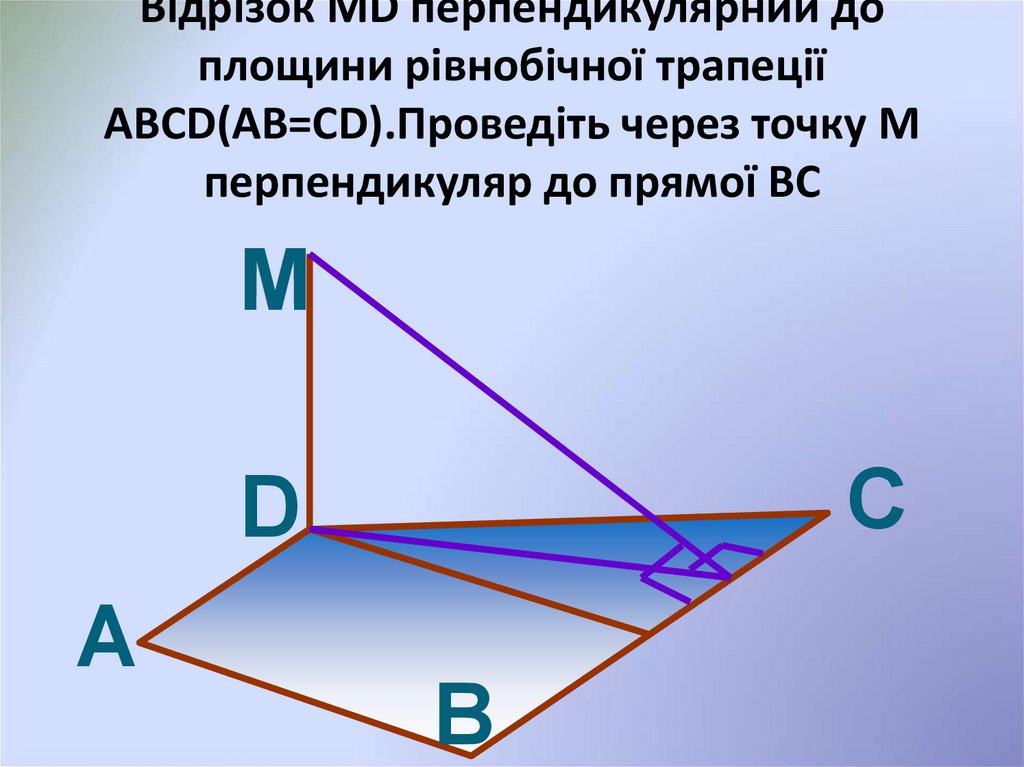
17. Відрізок MD перпендикулярний до площини рівнобічної трапеції ABCD(AB=CD).Проведіть через точку М перпендикуляр до прямої ВС

M
C
D
A
B

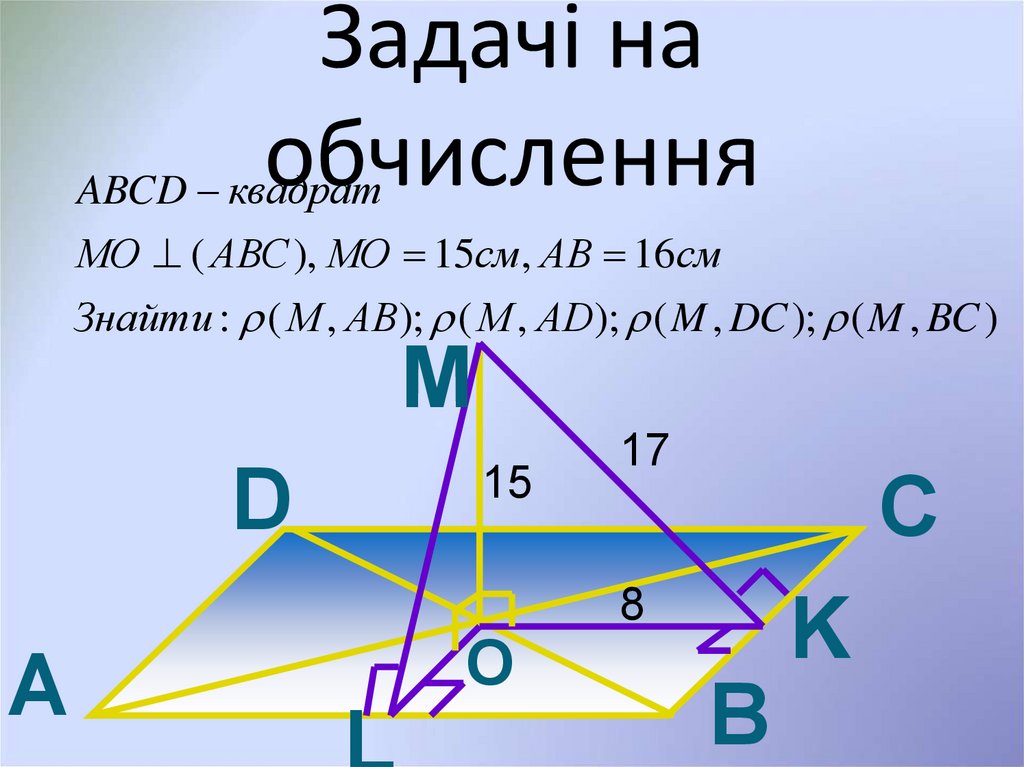
18. Задачі на обчислення

ABCD квадрат
МО ( АВС ), МО 15см, АВ 16см
Знайти : ( М , АВ); ( М , АD); ( M , DC ); ( M , BC )
M
D
15
17
C
8
A
O
K
B

19.

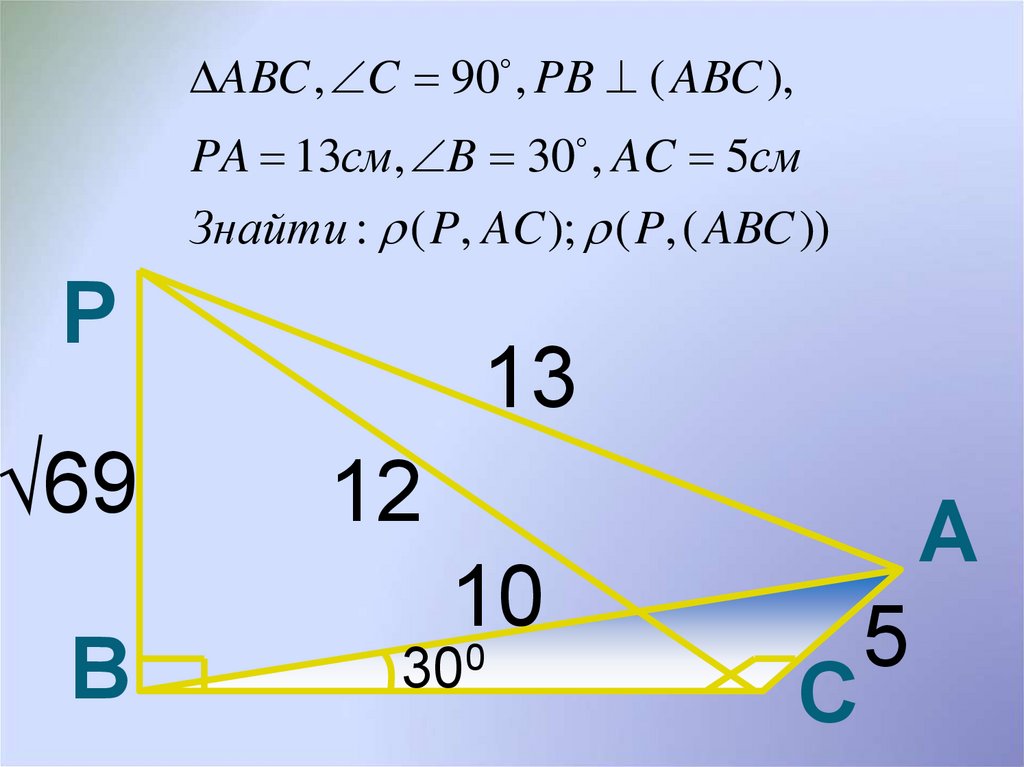
ABC , C 90 , PB ( ABC ),
PA 13см, B 30 , AC 5см
Знайти : ( P, AC ); ( P, ( ABC ))
P
√69
B
13
12
A
10
300
C
5

20.

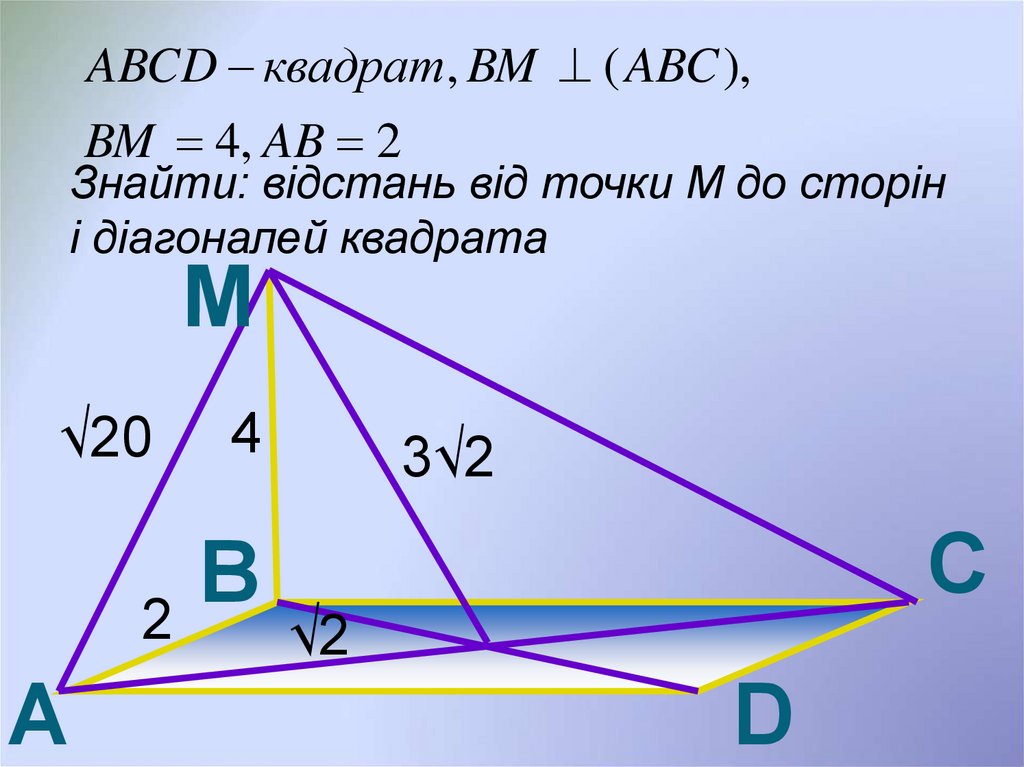
ABCD квадрат, BM ( ABC ),
BM 4, AB 2
Знайти: відстань від точки М до сторін
і діагоналей квадрата
M
√20
4
B
2
A
3√2
C
√2
D

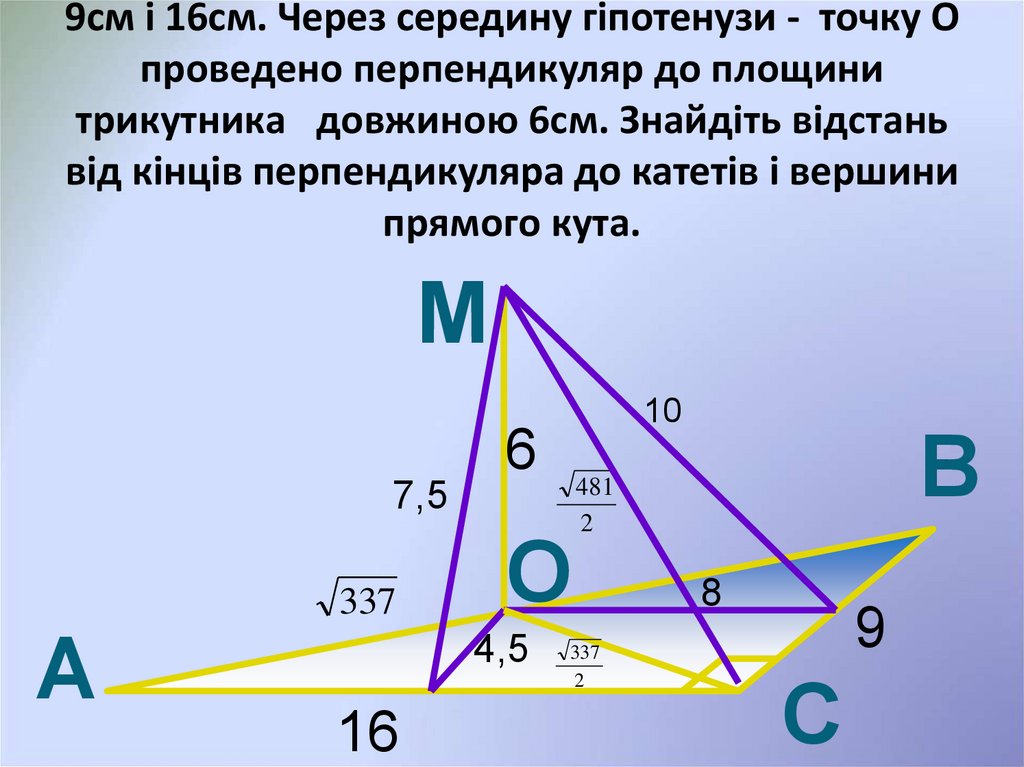
21. Катети прямокутного трикутника АВС рівні 9см і 16см. Через середину гіпотенузи - точку О проведено перпендикуляр до площини

9см і 16см. Через середину гіпотенузи - точку О
проведено перпендикуляр до площини
трикутника довжиною 6см. Знайдіть відстань
від кінців перпендикуляра до катетів і вершини
прямого кута.
M
7,5
337
A
6
B
481
2
O
4,5
16
10
337
2
8
9
C

22.

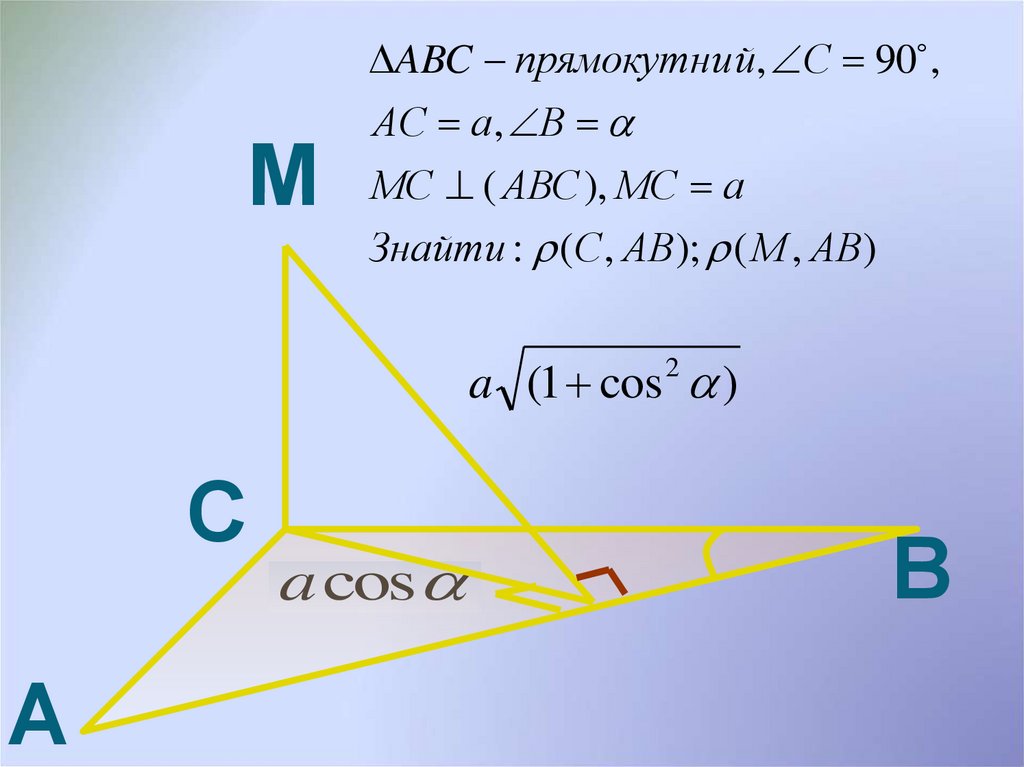
ABC прямокутни й, С 90 ,
M
АС а, В
МС ( АВС ), МС а
Знайти : (С , АВ); ( М , АВ)
a (1 cos 2 )
C
A
a cos
B

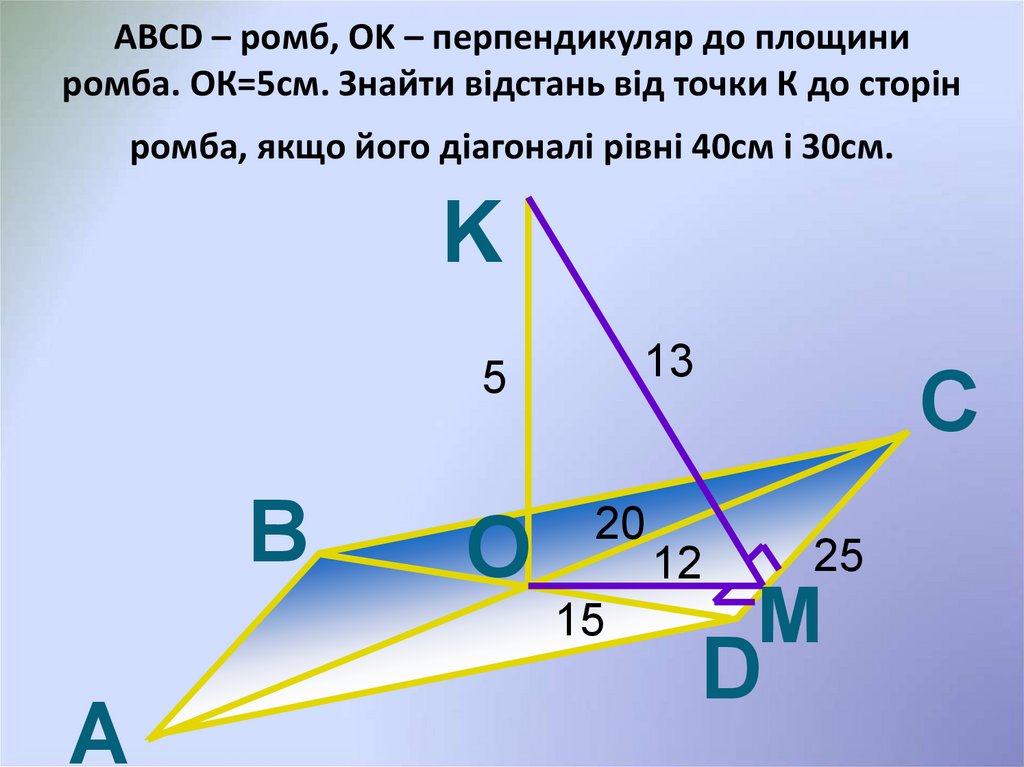
23. ABCD – ромб, OK – перпендикуляр до площини ромба. ОК=5см. Знайти відстань від точки К до сторін ромба, якщо його діагоналі

рівні 40см і 30см.
K
13
5
B
O
20
15
A
C
12
25
M
D

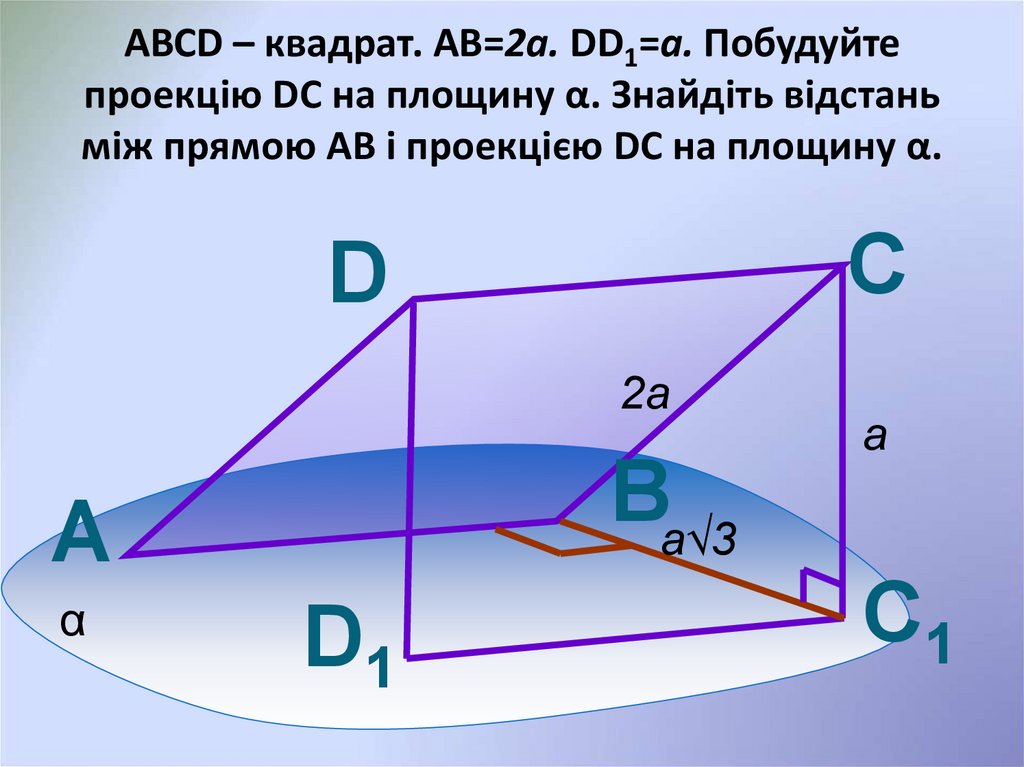
24. ABCD – квадрат. АВ=2а. DD1=a. Побудуйте проекцію DC на площину α. Знайдіть відстань між прямою АВ і проекцією DC на площину α.

C
D
2a
Ba√3
A
α
a
D1
C1