Похожие презентации:
Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої
1. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої
2. Перпендикулярні відрізки
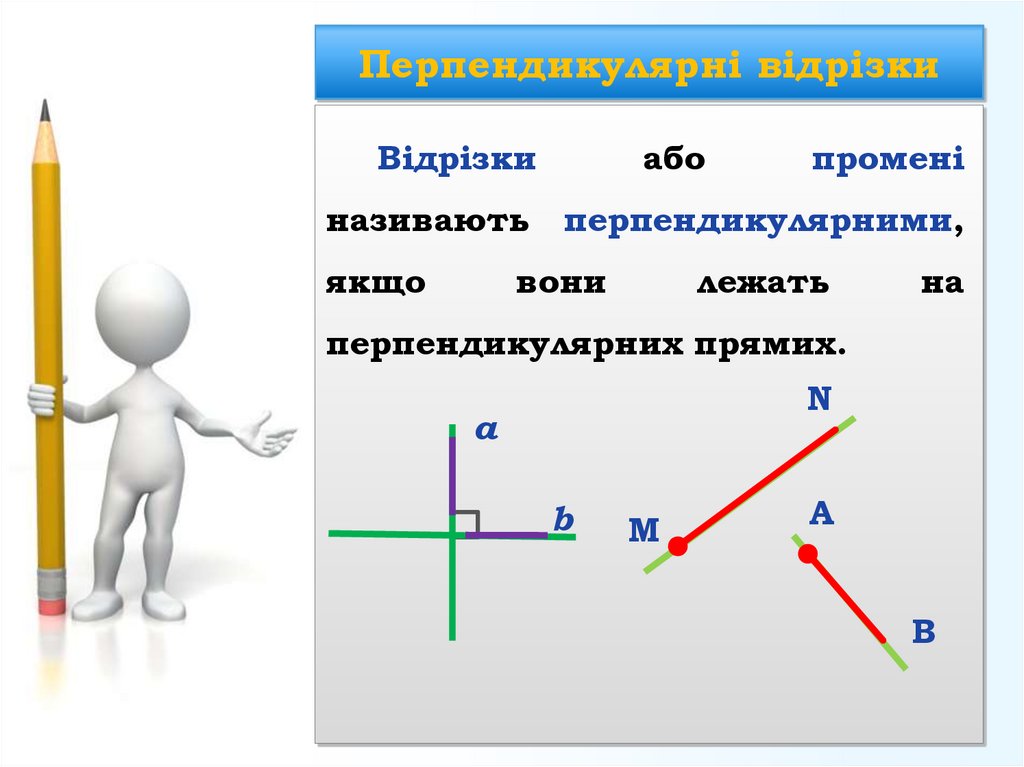
Відрізкиабо
промені
називають перпендикулярними,
якщо
вони
лежать
на
перпендикулярних прямих.
N
а
b
М
А
В
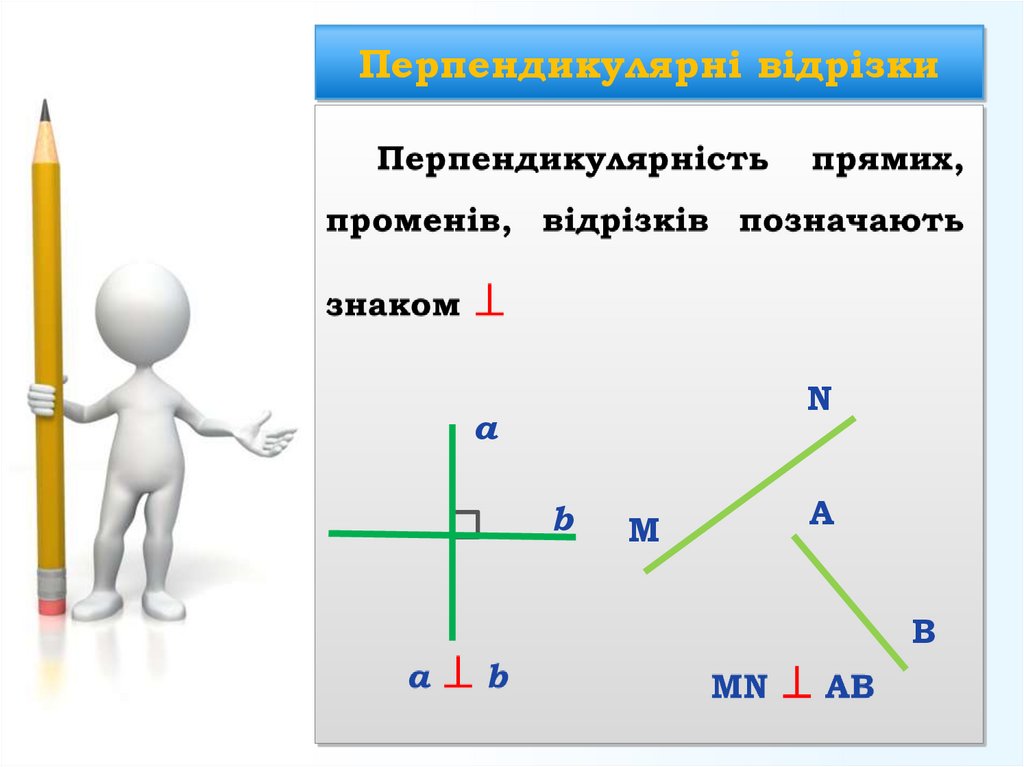
3. Перпендикулярні відрізки
Nа
b
М
А
В
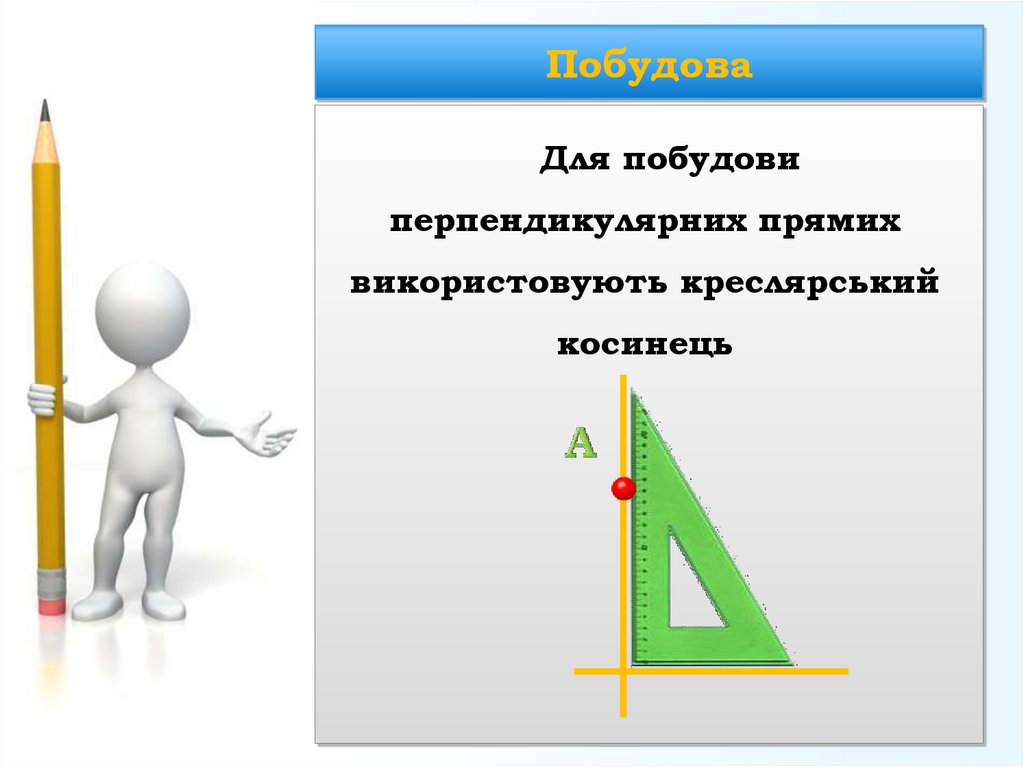
4. Побудова
Для побудовиперпендикулярних прямих
використовують креслярський
косинець
5. Перпендикуляр
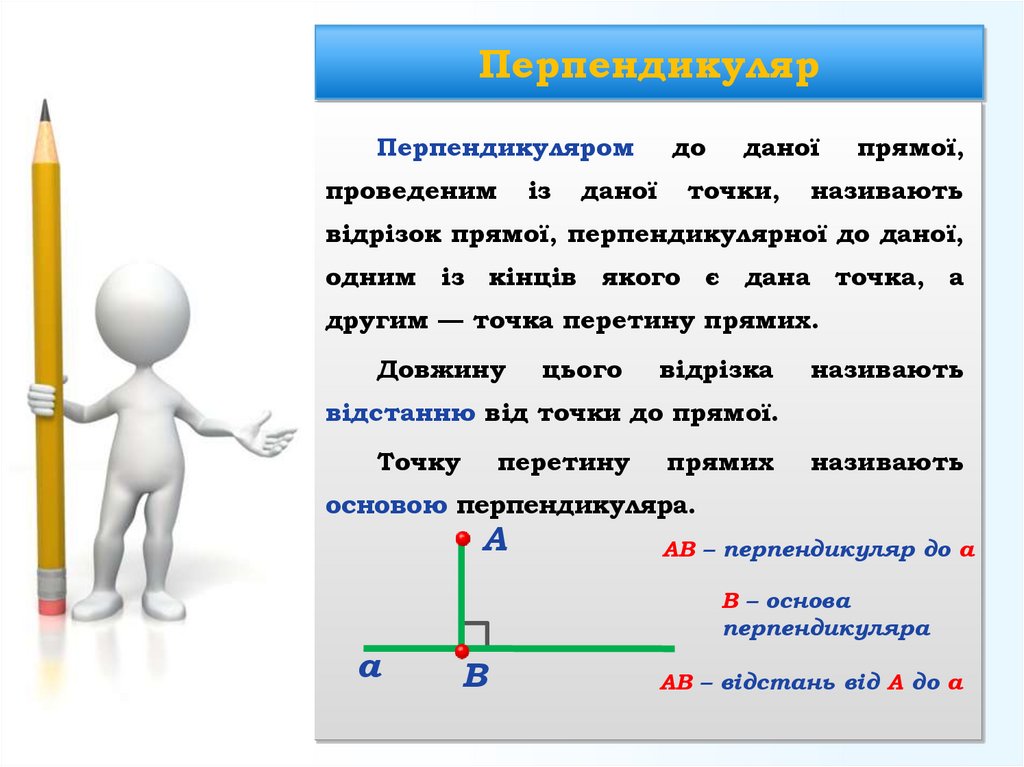
Перпендикуляромпроведеним
із
даної
до
даної
точки,
прямої,
називають
відрізок прямої, перпендикулярної до даної,
одним із кінців якого є дана точка, а
другим — точка перетину прямих.
Довжину
цього
відрізка
називають
відстанню від точки до прямої.
Точку
перетину
прямих
називають
основою перпендикуляра.
А
АВ – перпендикуляр до а
В – основа
перпендикуляра
а
В
АВ – відстань від А до а
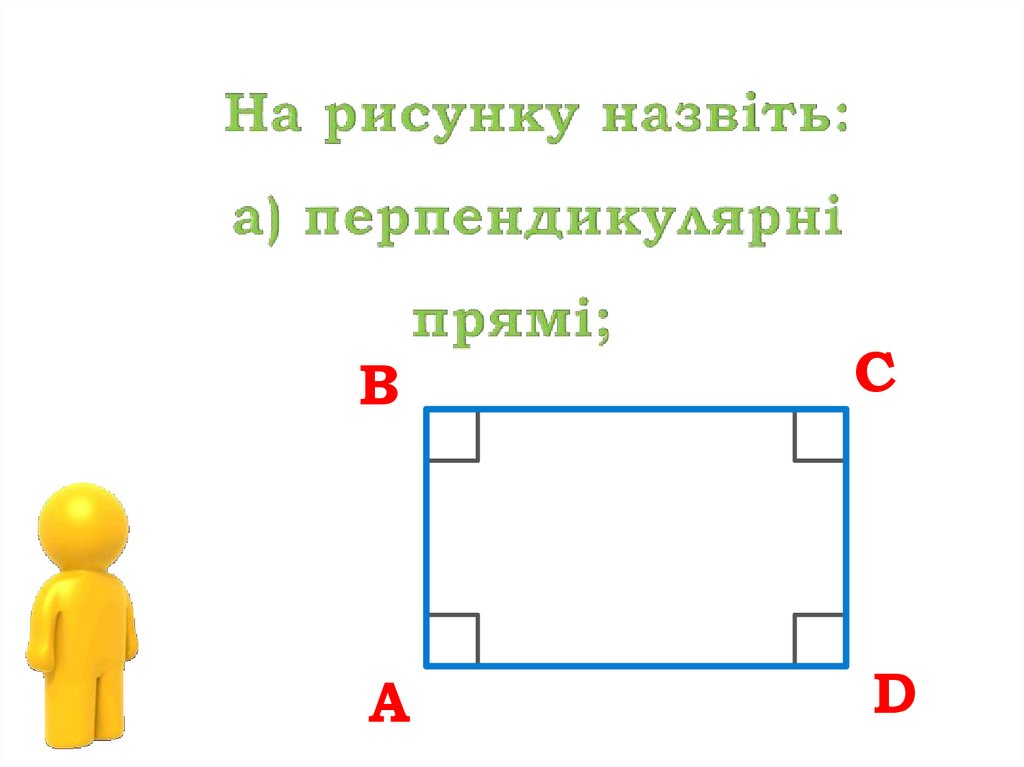
6. Закріплення
7.
ВА
С
D
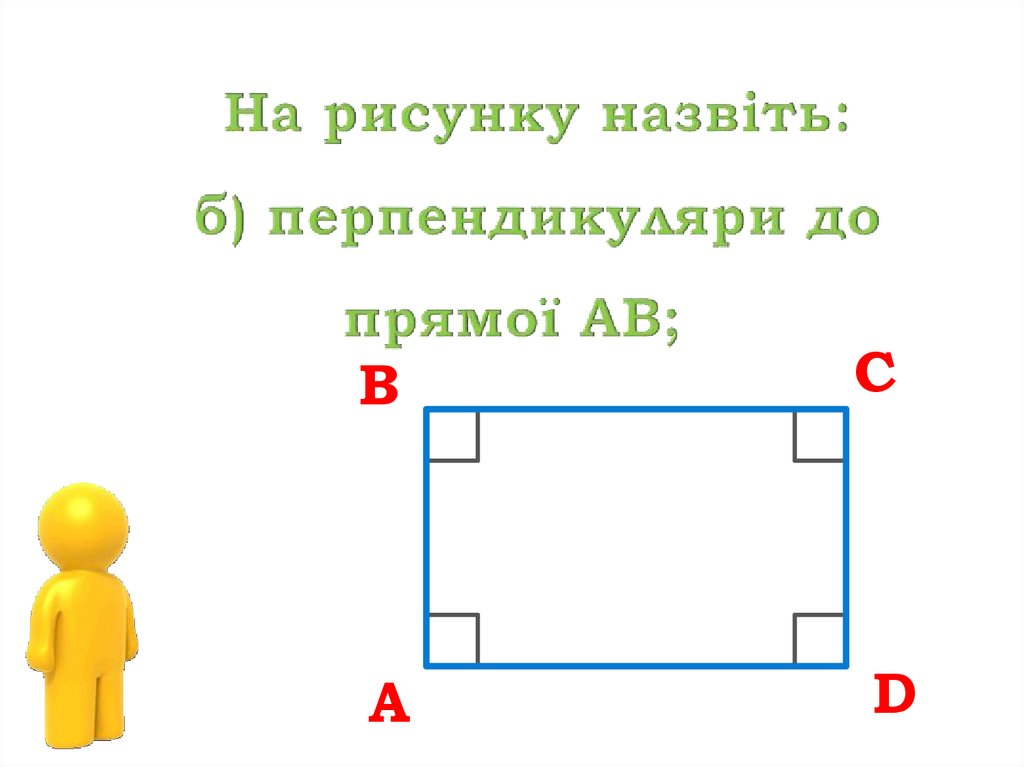
8.
ВА
С
D
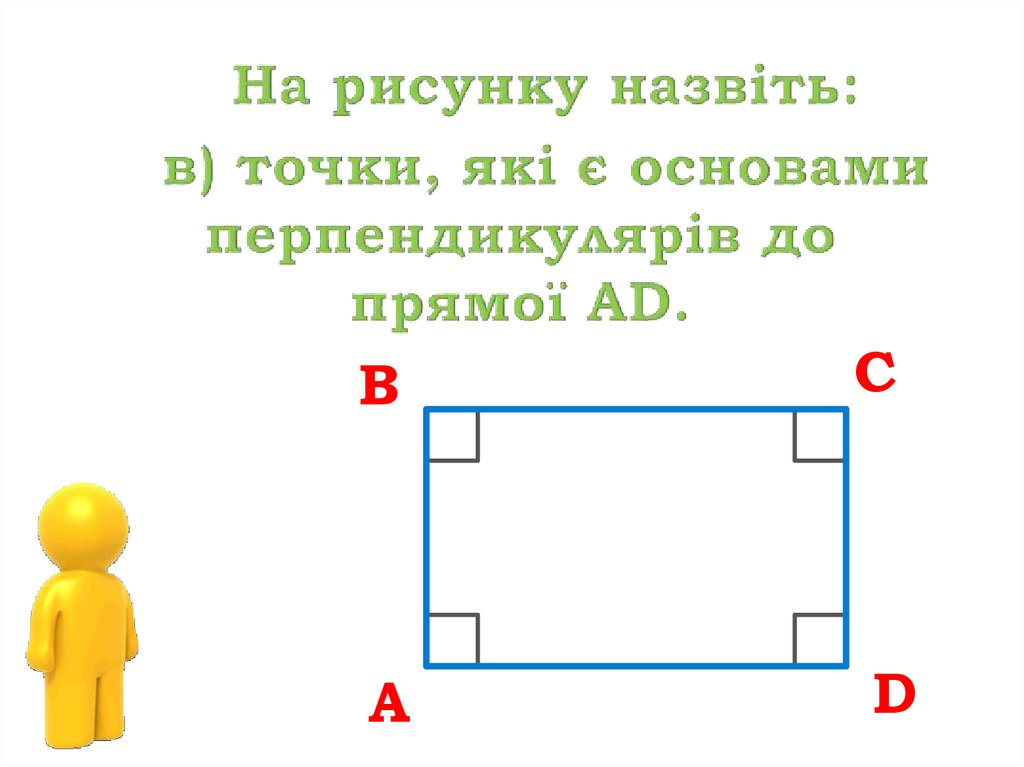
9.
ВА
С
D
10.
11.
12. Паралельні прямі
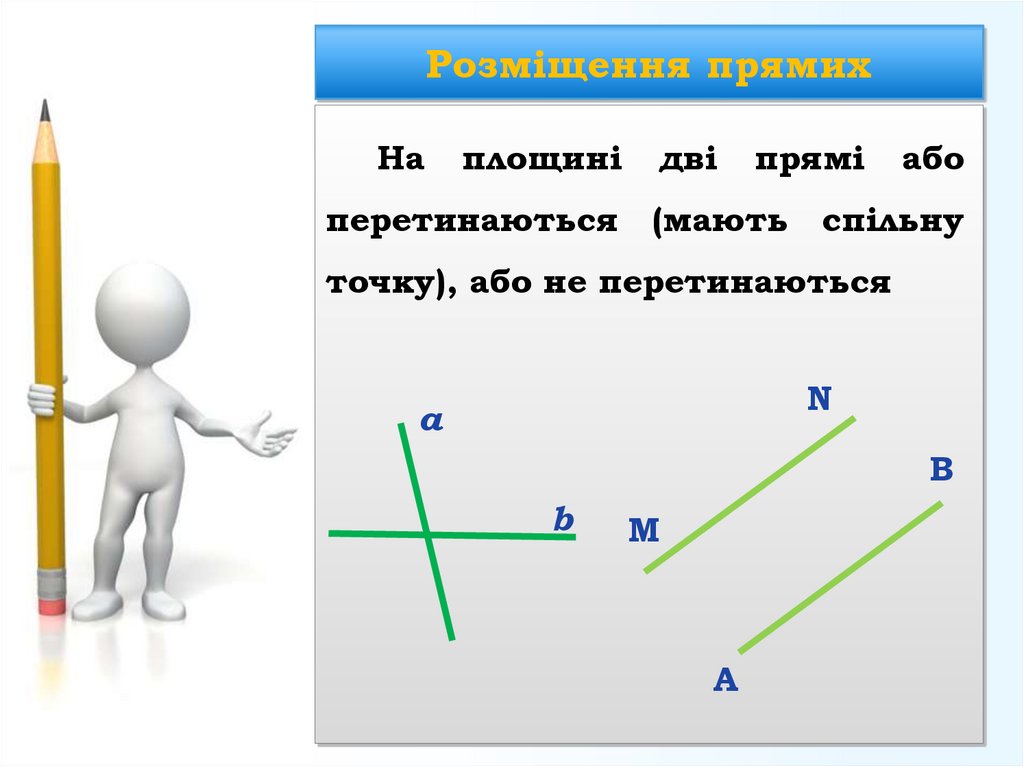
13. Розміщення прямих
Наплощині
дві
прямі
або
перетинаються (мають спільну
точку), або не перетинаються
N
а
В
b
М
А
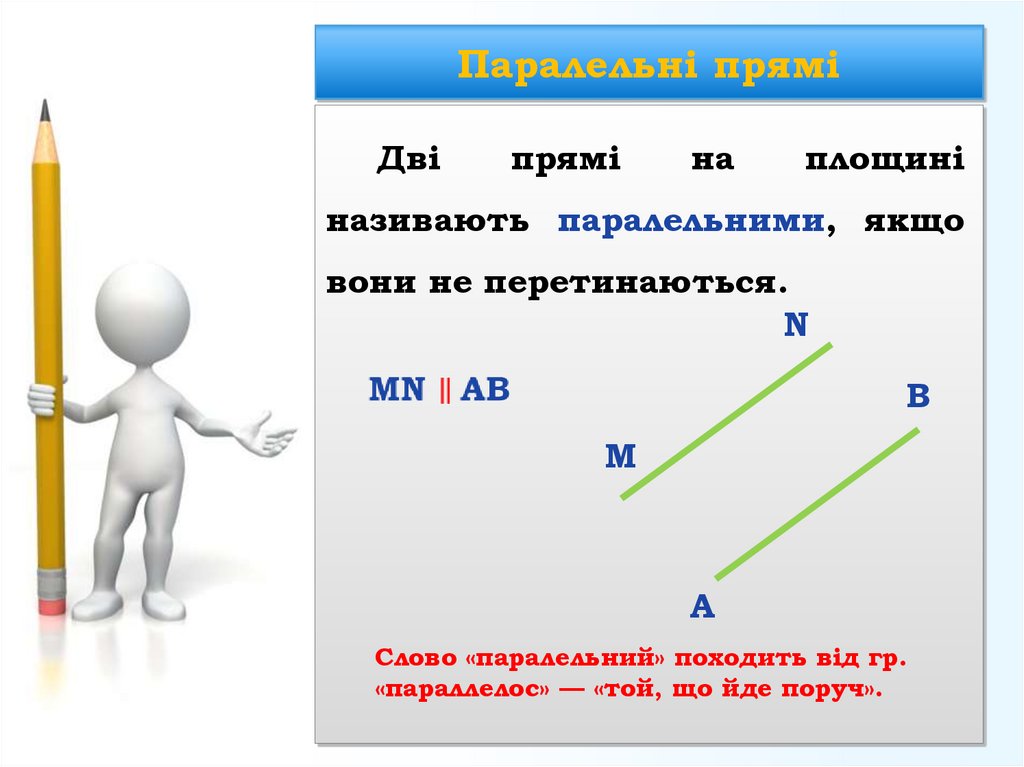
14. Паралельні прямі
Двіпрямі
на
площині
називають паралельними, якщо
вони не перетинаються.
N
В
М
А
Слово «паралельний» походить від гр.
«параллелос» — «той, що йде поруч».
15.
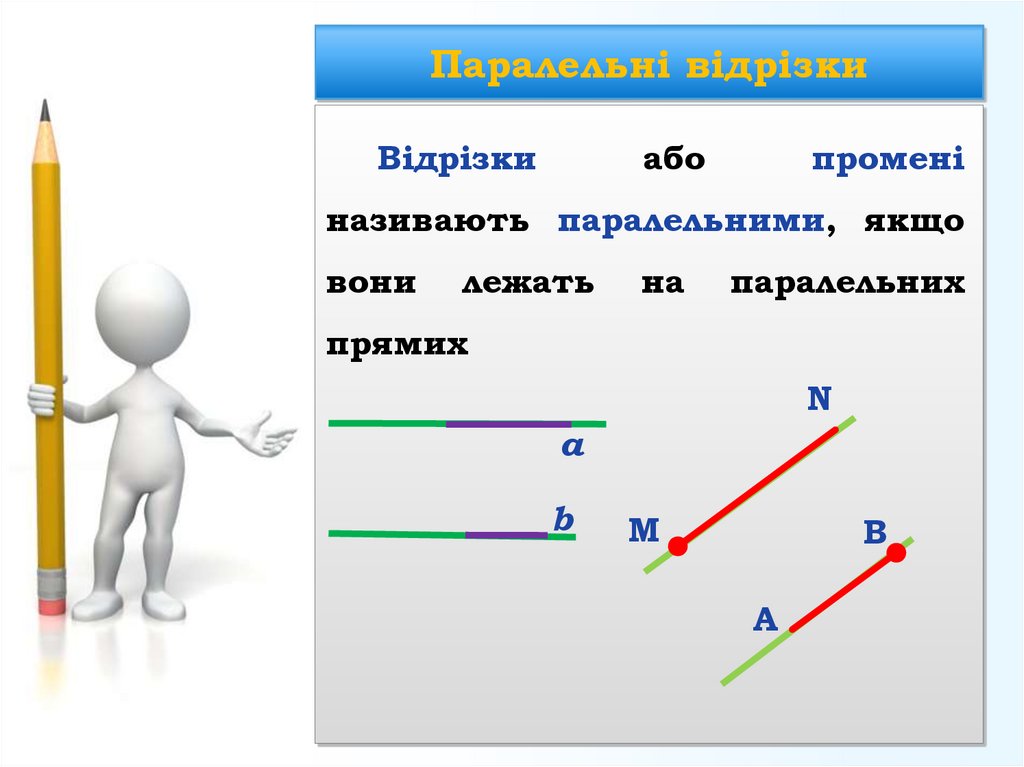
16. Паралельні відрізки
Відрізкиабо
промені
називають паралельними, якщо
вони
лежать
на
паралельних
прямих
N
а
b
М
В
А
17. Аксіома паралельності прямих
Через точку, що не лежить наданій прямій, можна провести
тільки одну пряму, паралельну
даній.
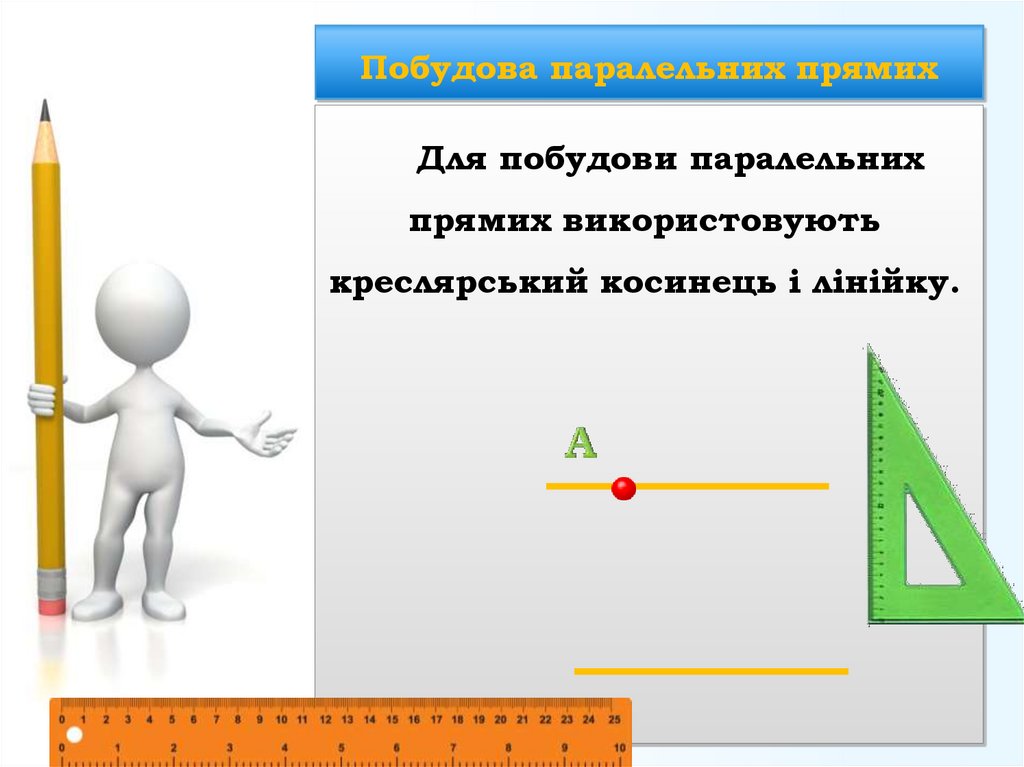
18. Побудова паралельних прямих
Для побудови паралельнихпрямих використовують
креслярський косинець і лінійку.
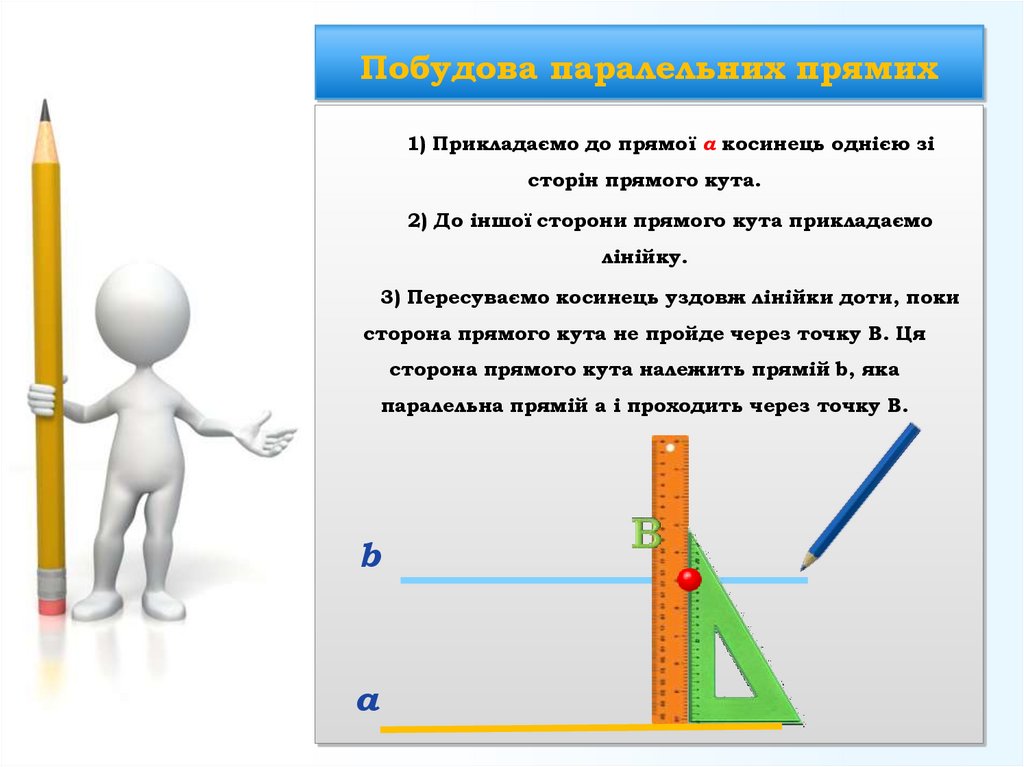
19. Побудова паралельних прямих
1) Прикладаємо до прямої a косинець однією зісторін прямого кута.
2) До іншої сторони прямого кута прикладаємо
лінійку.
3) Пересуваємо косинець уздовж лінійки доти, поки
сторона прямого кута не пройде через точку B. Ця
сторона прямого кута належить прямій b, яка
паралельна прямій a і проходить через точку B.
b
а
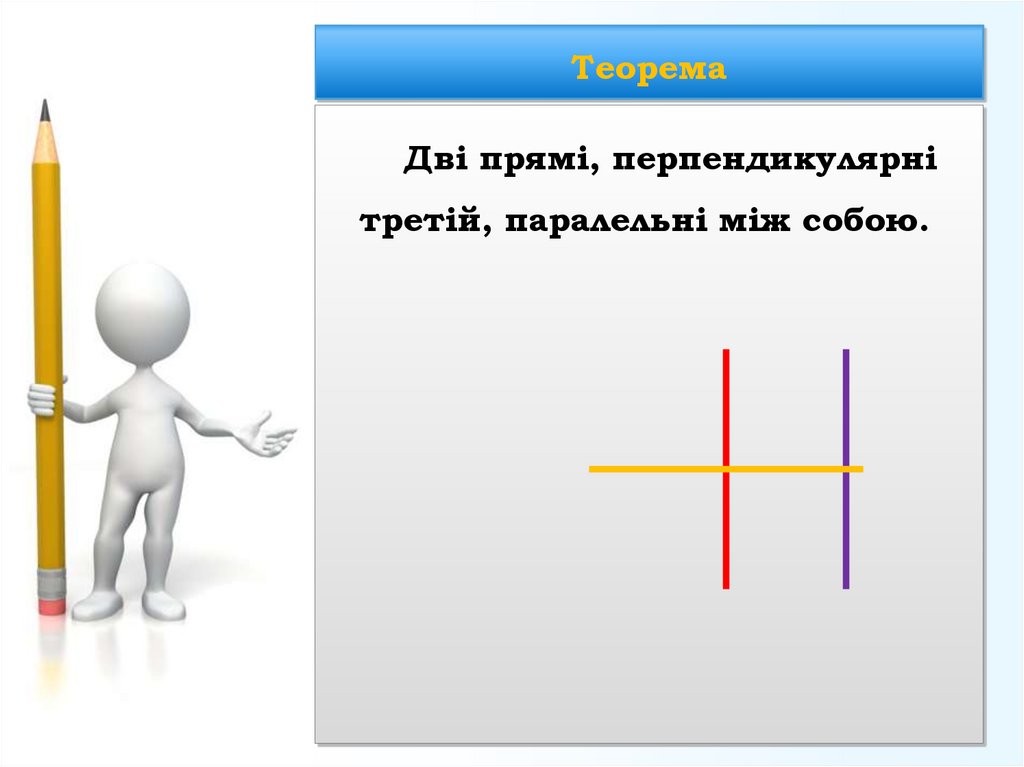
20. Теорема
Дві прямі, перпендикулярнітретій, паралельні між собою.
21. Теорема
Дві прямі, паралельні третій,паралельні між собою.
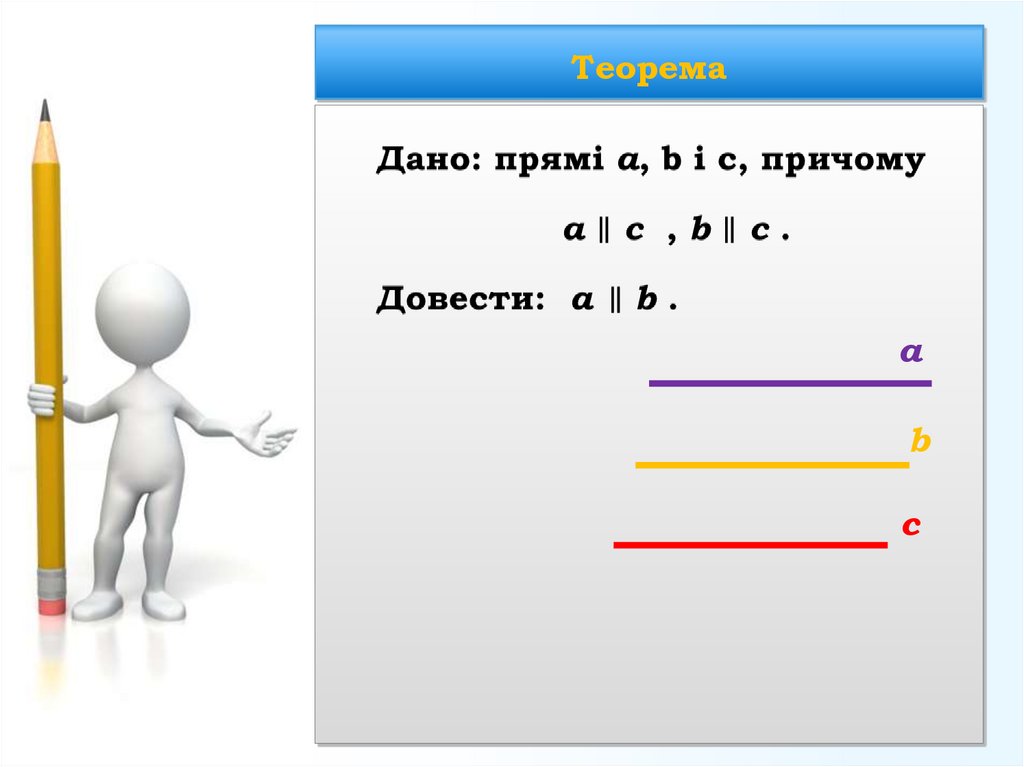
22. Теорема
аb
с
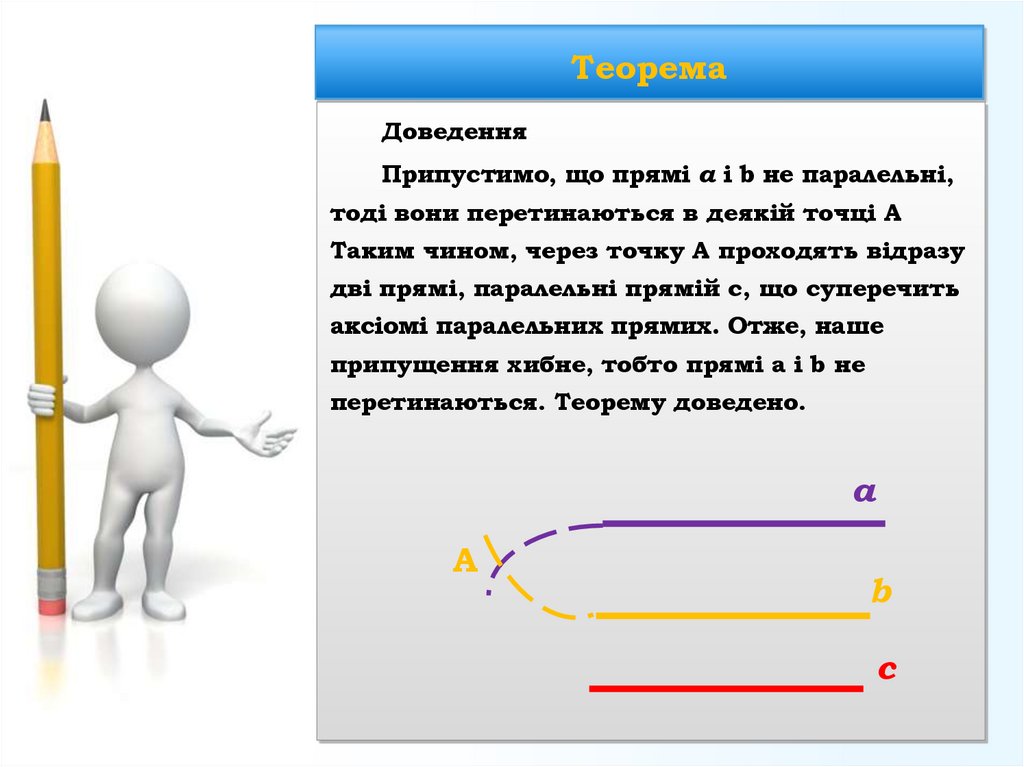
23. Теорема
ДоведенняПрипустимо, що прямі a і b не паралельні,
тоді вони перетинаються в деякій точці A
Таким чином, через точку A проходять відразу
дві прямі, паралельні прямій c, що суперечить
аксіомі паралельних прямих. Отже, наше
припущення хибне, тобто прямі a і b не
перетинаються. Теорему доведено.
а
А
b
с











 Математика
Математика








