Похожие презентации:
Спецификация уравнения множественной регрессии. Выбор формы зависимости
1. Спецификация уравнения множественной регрессии. Выбор формы зависимости
Лекция2. Спецификация уравнения регрессии
Выбор переменных(предыдущая лекция)
Выбор формы зависимости
2
3. Цели лекции
1. Свести вместе все, что мы знаем овыборе
формы зависимости и рассмотреть
особенности многомерного случая
2. Изучить последствия неправильного
выбора функциональной формы
3. Найти средства, позволяющие улучшить
качество выбора формы связи
3
4. Роль постоянного члена регрессии
1. Свободный член абсорбирует все смещения исдвиги
2. Исключение постоянного члена приводит к
нарушению предпосылки 10 теоремы ГауссаМаркова о равенстве нулю математического
ожидания случайного отклонения
4
5. Интерпретация постоянного члена регрессии
1. Постоянный член задает точку пересеченияграфика уравнения регрессии с осью Y
2. Интерпретируется как ожидаемое значение Y,
когда объясняющие переменные и случайный
член равны нулю
Иногда постоянный член имеет содержательный смысл
5
6. Пример роли постоянного члена. Анализ затрат
Ci 0 1Qi i0 постоянные затраты, 1Q переменные затраты
Если постоянные затраты малы, то можно исключить
свободный член, получив лишнюю степень свободы
Исключение постоянного члена всегда должно быть
обосновано экономически
Необоснованное исключение из уравнения регрессии
постоянного члена приводит к серьезным ошибкам!
6
7. Последствия исключения постоянного члена
1. Оценки коэффициентов при переменныхискажаются и смещаются
2. t-статистики становятся некорректными
tj
bj
Sb j
7
8. Роль постоянного члена регрессии. Выводы
Выводы:1. За редкими и обоснованными исключениями
не следует исключать постоянный член из
уравнения регрессии
2. Не следует полагаться на оценку самого
постоянного члена
8
9. Выбор формы зависимости
Альтернативные функциональные формы1. Линейные зависимости
2. Нелинейные зависимости, приводящиеся
преобразованием переменных к линейным
3. Нелинейные зависимости, не приводящиеся
преобразованием переменных к линейным
9
10. Линейные зависимости
Y 0 1 X 1 2 X 2 m X mИнтерпретация коэффициентов регрессии: предельные
эффекты факторов (при постоянстве прочих факторов)
dY
Y
k
dX k
X k
Вычисление эластичностей
dY / dX k
dY X k
Xk
L(Y , X k )
k
Y / Xk
dX k Y
Y
Анализ эластичностей – мощное средство анализа зависимостей
10
11. Логарифмические зависимости
ln Y 0 1 ln X 1 2 ln X 2 m ln X mИнтерпретация коэффициентов регрессии: являются
непосредственно факторными эластичностями
% Y
Y X k
L(Y , X k )
k
% X k X k Y
Теперь наклон переменный
dY dY X k Y
Y
Наклон(Y , X k )
k
,
dX k dX k Y X k
Xk
11
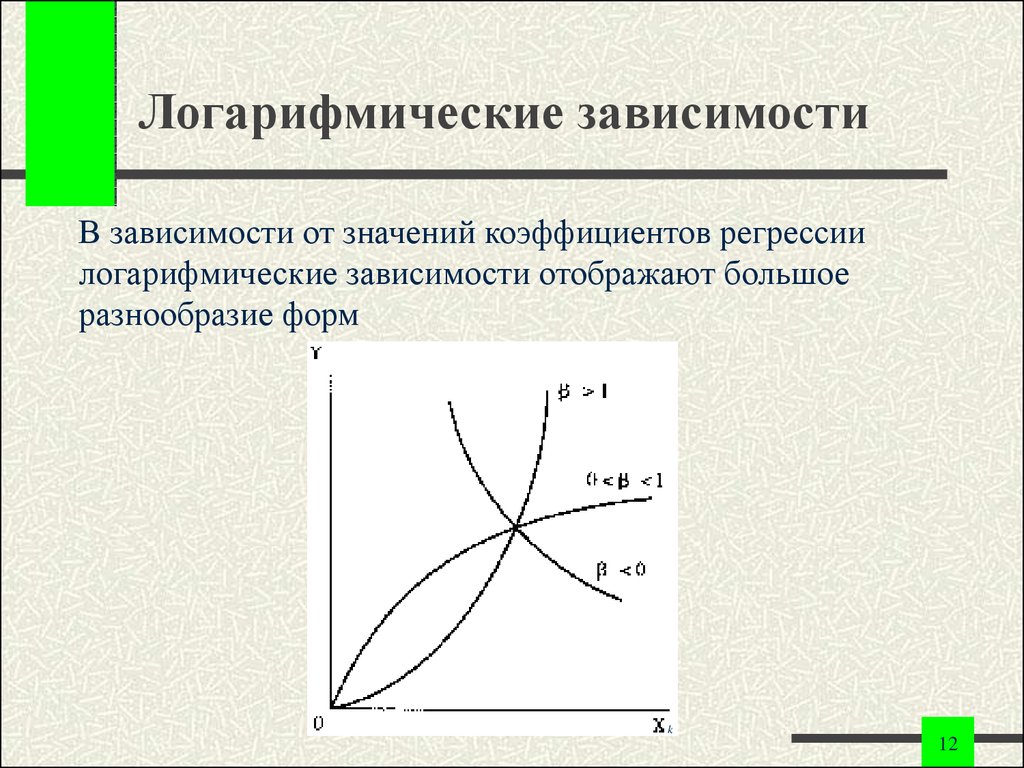
12. Логарифмические зависимости
В зависимости от значений коэффициентов регрессиилогарифмические зависимости отображают большое
разнообразие форм
k
12
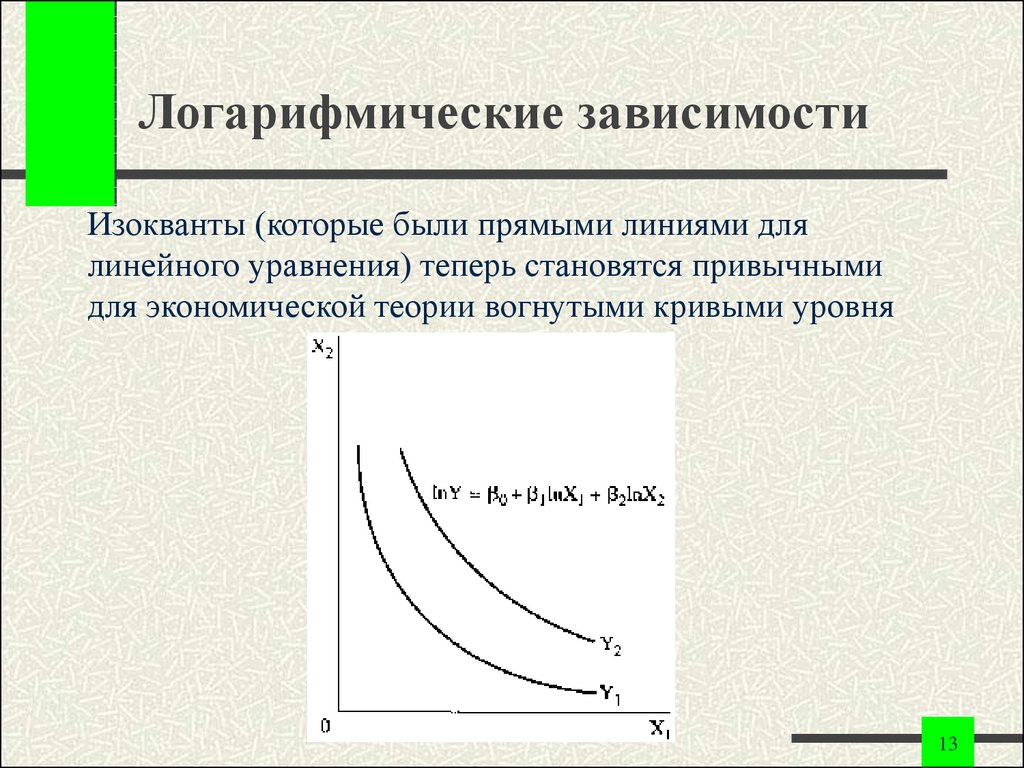
13. Логарифмические зависимости
Изокванты (которые были прямыми линиями длялинейного уравнения) теперь становятся привычными
для экономической теории вогнутыми кривыми уровня
13
14. Пример. Производственная функция Кобба-Дугласа
Y AK L vЗамена переменных делает уравнение линейным
ln Y ln A ln K ln L ln v
Сумма эластичностей указывает на эффект масштаба
1, 1, 1
14
15. Пример. Производственная функция Кобба-Дугласа
Оценивание производственной функции приограничении на эффект масштаба
1
Y AK L v
Переходим к удельным величинам (на единицу труда)
Y / L A( K / L) v
Теперь переход к логарифмам позволяет получить оценку
ln( Y / L) ln A ln( K / L) ln v
15
16. Пример. Производственная функция Кобба-Дугласа
Учет и оценка технического прогрессаrt
Y AK L e v
После логарифмирования
ln Y ln A ln K ln L rt ln v
Здесь также можно использовать ограничение на эффект
масштаба
16
17. Линейно-логарифмические зависимости
Yi 0 1 ln X 1 2 X 2В нелинейной паре коэффициент наклона рассчитывается как:
dY
1
dX 1 X 1
dY
Y
1
dX 1 / X 1
( X 1 / X 1 )
Вычисление эластичности:
dY / dX 1 dY X 1 k
L(Y , X 1 )
Y / X1
dX 1 Y
Y
17
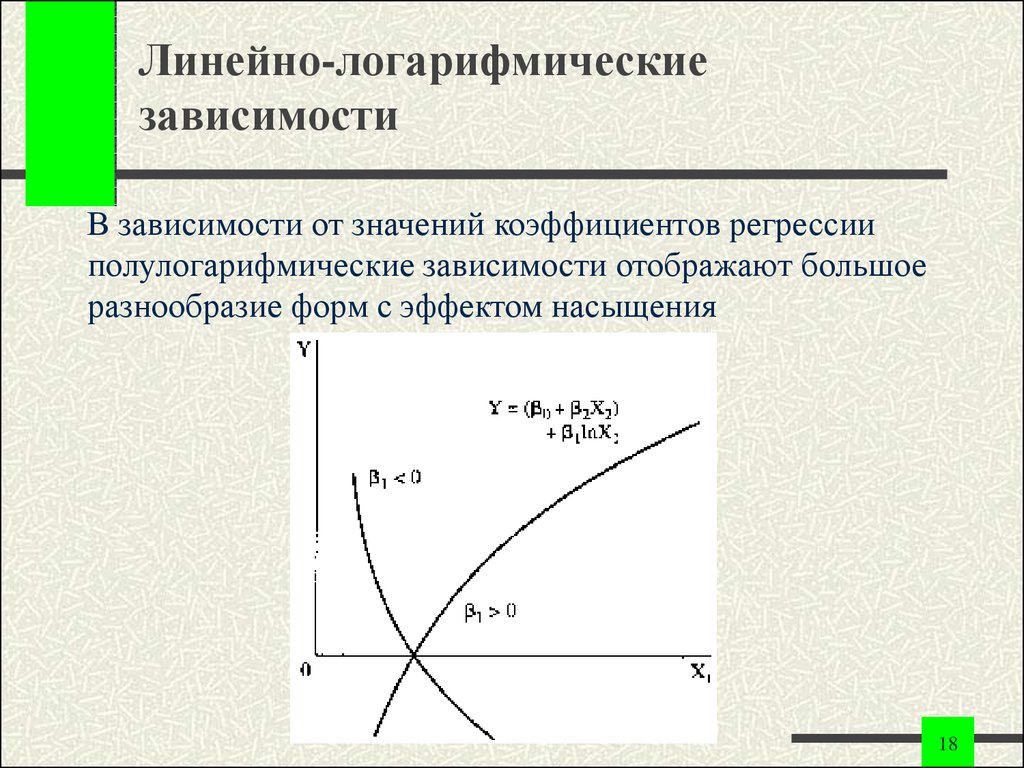
18. Линейно-логарифмические зависимости
В зависимости от значений коэффициентов регрессииполулогарифмические зависимости отображают большое
разнообразие форм с эффектом насыщения
18
19. Логарифмически-линейные зависимости
ln Y 0 1 X 1 2 X 2Наклон:
1Y
Эластичность:
1 X 1
Эти функции хорошо подходят для моделирования
эффектов, которые проявляются в процентном
выражении в ответ на абсолютный рост факторов
(например, вознаграждение)
19
20. Полиномиальные формы зависимости
Y 0 1 X 1 2 X 3 X 22
1
Наклон:
Эластичность:
dY
1 2 2 X 1
dX 1
% Y
X1
X 12
1
2 2
% X 1
Y
Y
Эти функции хорошо подходят для моделирования
эффекта масштаба, анализа максимумов и
минимумов
20
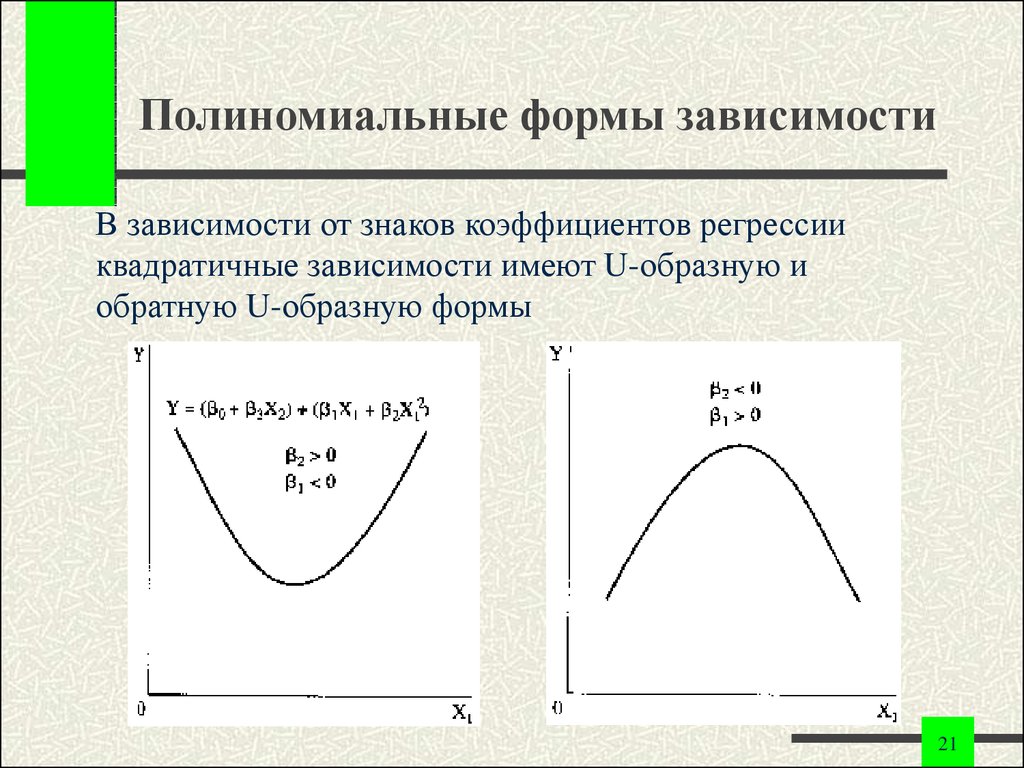
21. Полиномиальные формы зависимости
В зависимости от знаков коэффициентов регрессииквадратичные зависимости имеют U-образную и
обратную U-образную формы
21
22. Обратные формы зависимости
1Y 0 1
2 X 2
X1
Наклон:
Эластичность:
Асимптота:
dY
1
2
dX 1
X1
% Y
1
% X 1
YX 1
Y 0 2 X 2
Эти функции хорошо подходят для моделирования
эффектов полного насыщения и ограниченности
22
23. Сводка результатов для альтернативных форм связи
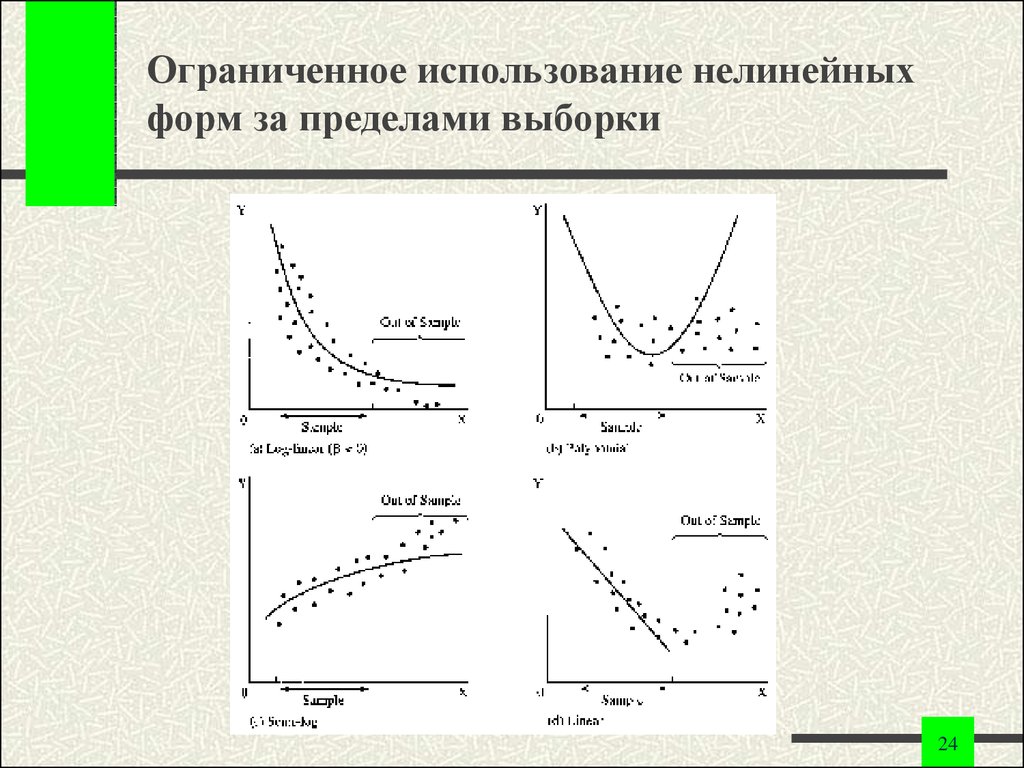
2324. Ограниченное использование нелинейных форм за пределами выборки
2425. Последствия неправильного использования функциональных форм
1. Ухудшение статистических характеристик(качества) уравнения (не всегда)
2. Невозможность использования построенных
уравнений за пределами выборки
Коэффициенты детерминации (обычный
и скорректированный) для различных
функциональных форм несравнимы
25
26. Нелинейный метод наименьших квадратов
Используется в тех случаях, когда уравнение неприводится с помощью преобразований
переменных к линейной форме
Пример: Кривая Филлипса
INFt 0
1
UNRt 1 2
26
27. Пример. Кривая Филлипса
21
min
Q INFt INFt INFt 0
UNRt 1 2
t
t
2
Нетрудно убедиться, что система уравнений
Q
0,
j
j 0,1,2
является нелинейной относительно неизвестных
параметров j , j 0,1,2
27
28. Нелинейный метод наименьших квадратов. Способы реализации
Численные методы:1. Метод прямого поиска минимума функционала
Q( )
2. Методы приближенного решения системы
нелинейных уравнений:
Q
0,
j
j 0, m
28
29.
Конец лекции29
























 Математика
Математика








