Похожие презентации:
Теорема о трех перпендикулярах
1.
2. Цели урока
• Ввести понятие расстояния отточки до плоскости;
• Доказать теорему о трёх
перпендикулярах;
• Показать применение этой
теоремы при решении задач.
3. Ход урока
1. Организационный момент;2. Актуализация опорных
знаний;
3. Изучение нового
материала.
4.
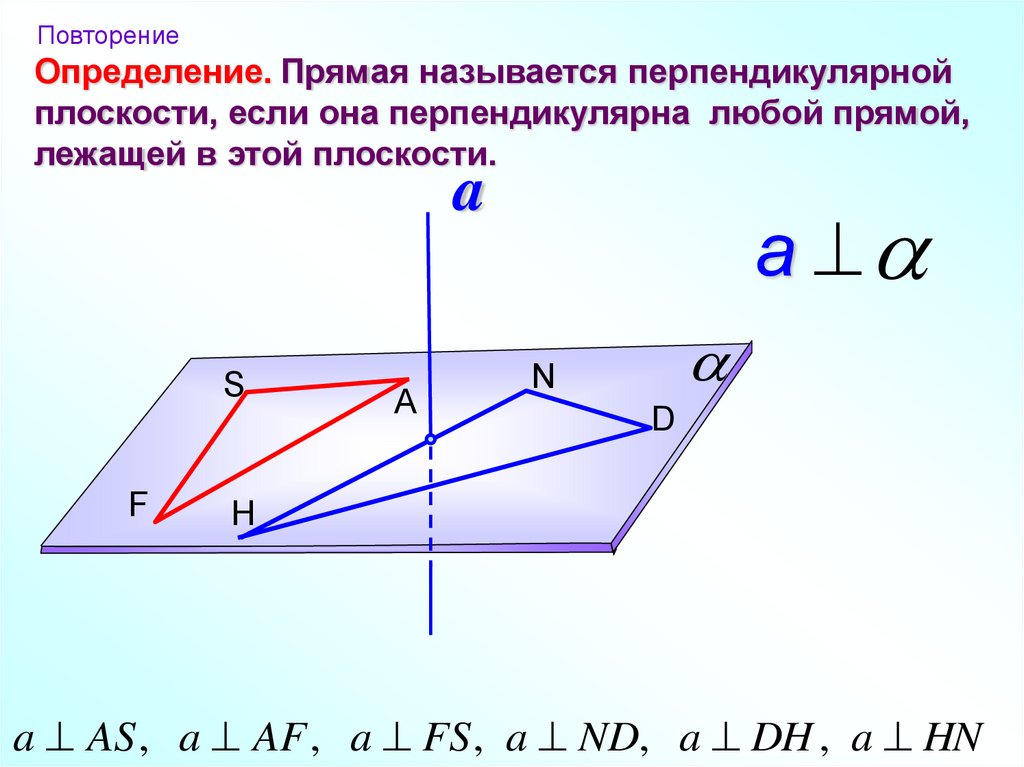
ПовторениеОпределение. Прямая называется перпендикулярной
плоскости, если она перпендикулярна любой прямой,
лежащей в этой плоскости.
a
S
F
A
a
N
D
H
a AS , a AF , a FS , a ND, a DH , a HN
5.
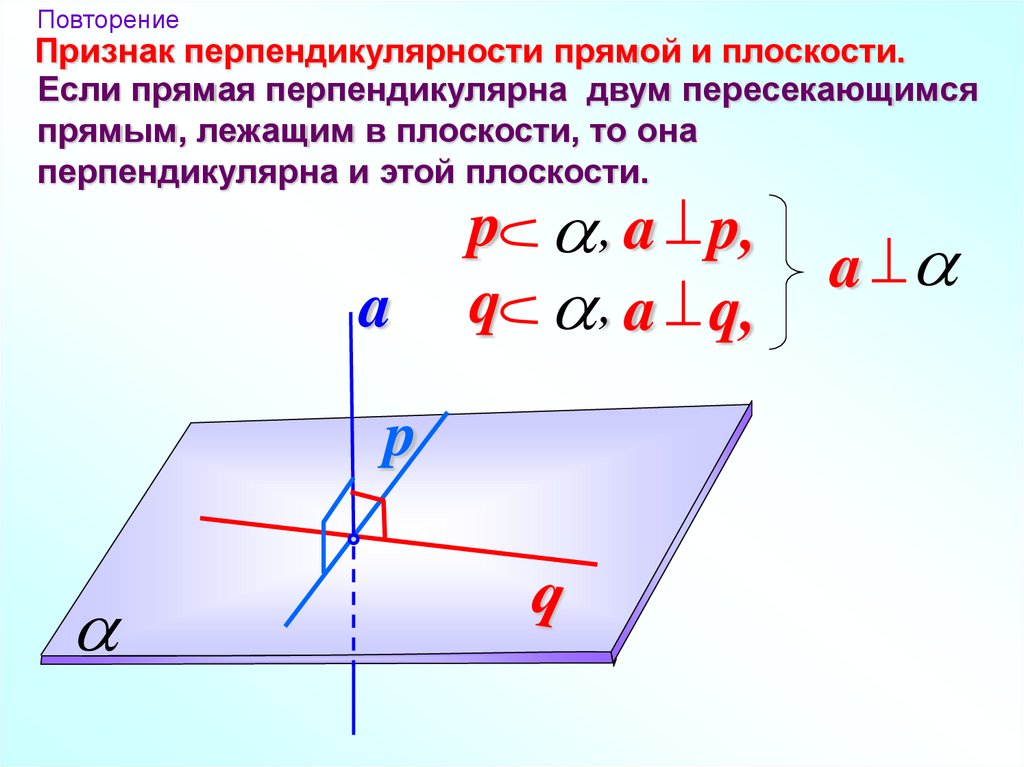
ПовторениеПризнак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся
прямым, лежащим в плоскости, то она
перпендикулярна и этой плоскости.
a
p
p , a p,
q , a q,
a
6.
ПланиметрияСтереометрия
А
А
а
М
Н
М
Н
Отрезок АН – перпендикуляр
Точка Н – основание перпендикуляра
Отрезок АМ – наклонная
Точка М – основание наклонной
Отрезок МН – проекция
наклонной на прямую а
Отрезок МН – проекция
наклонной на плоскость
7.
ПланиметрияСтереометрия
А
А
а
М
Н
Н
М
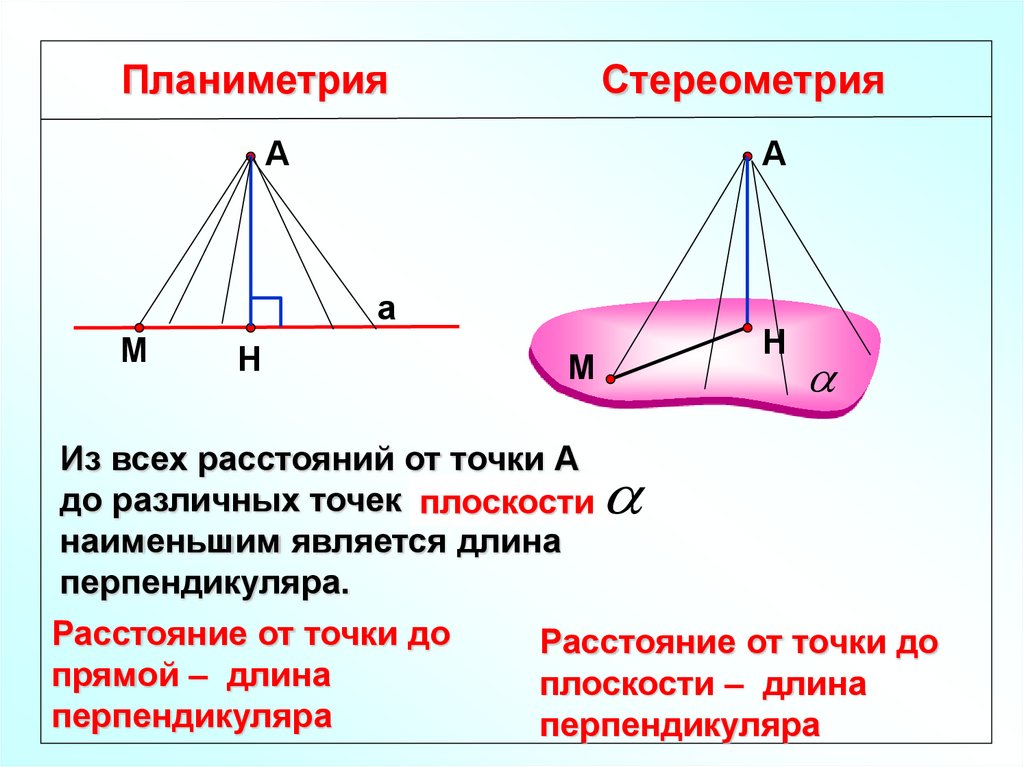
Из всех расстояний от точки А
до различных точек прямой
а
плоскости
наименьшим является длина
перпендикуляра.
Расстояние от точки до
Расстояние от точки до
прямой – длина
плоскости – длина
перпендикуляра
перпендикуляра
8.
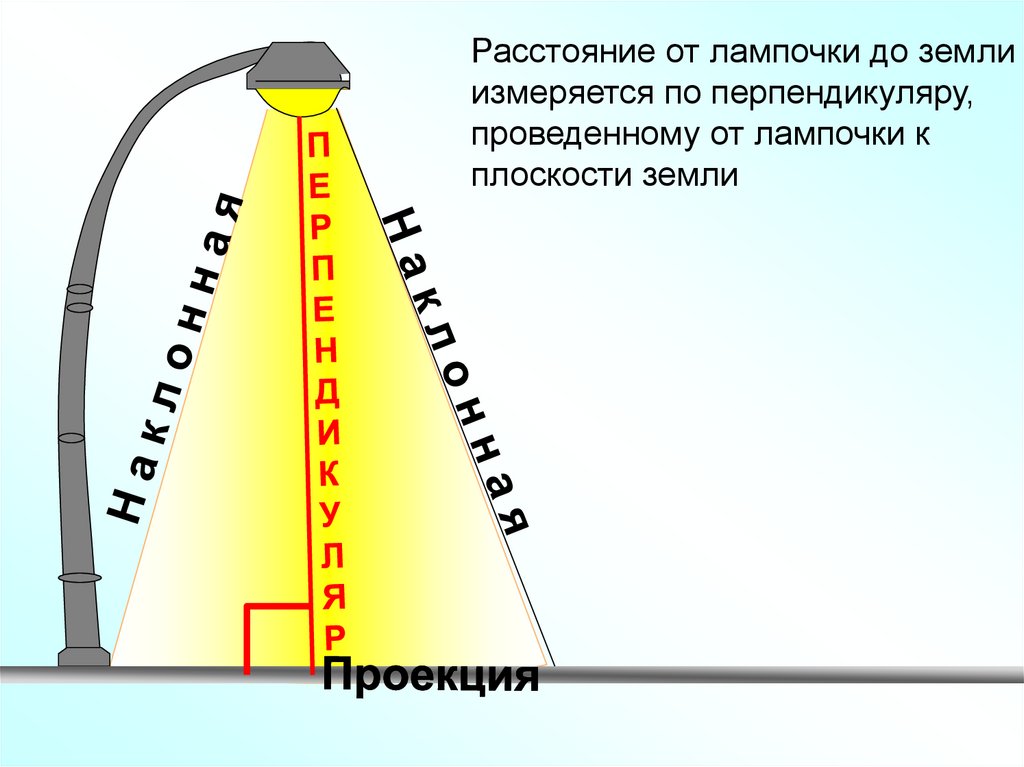
Расстояние от лампочки до землиизмеряется по перпендикуляру,
проведенному от лампочки к
плоскости земли
9.
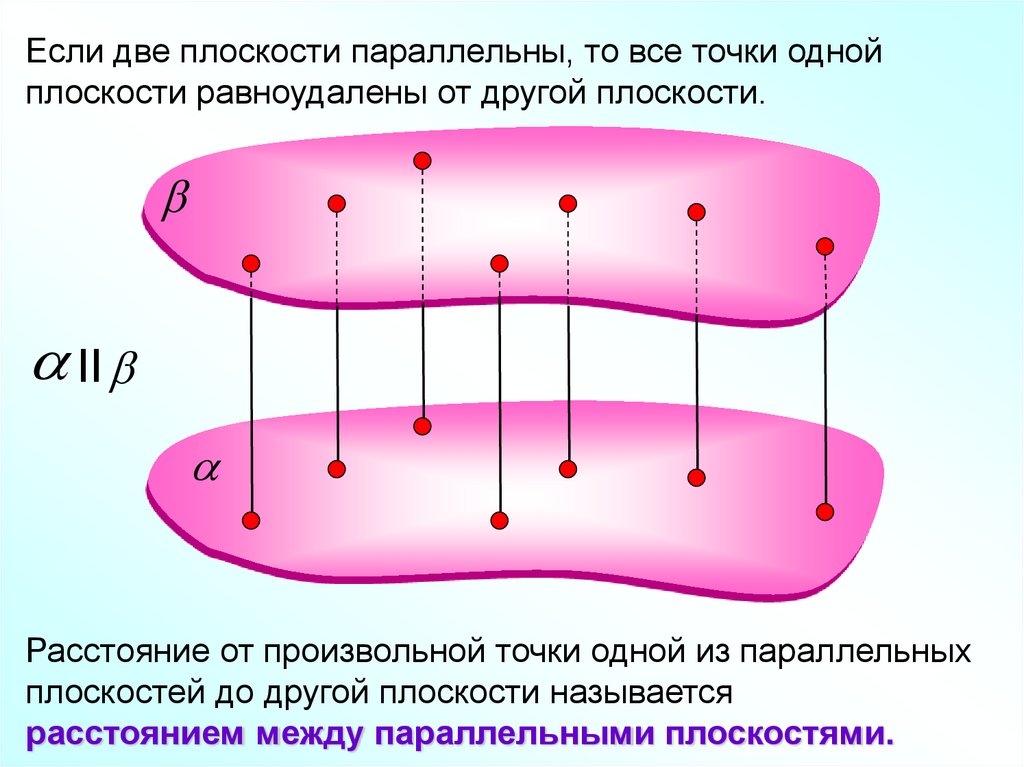
Если две плоскости параллельны, то все точки однойплоскости равноудалены от другой плоскости.
II
Расстояние от произвольной точки одной из параллельных
плоскостей до другой плоскости называется
расстоянием между параллельными плоскостями.
10.
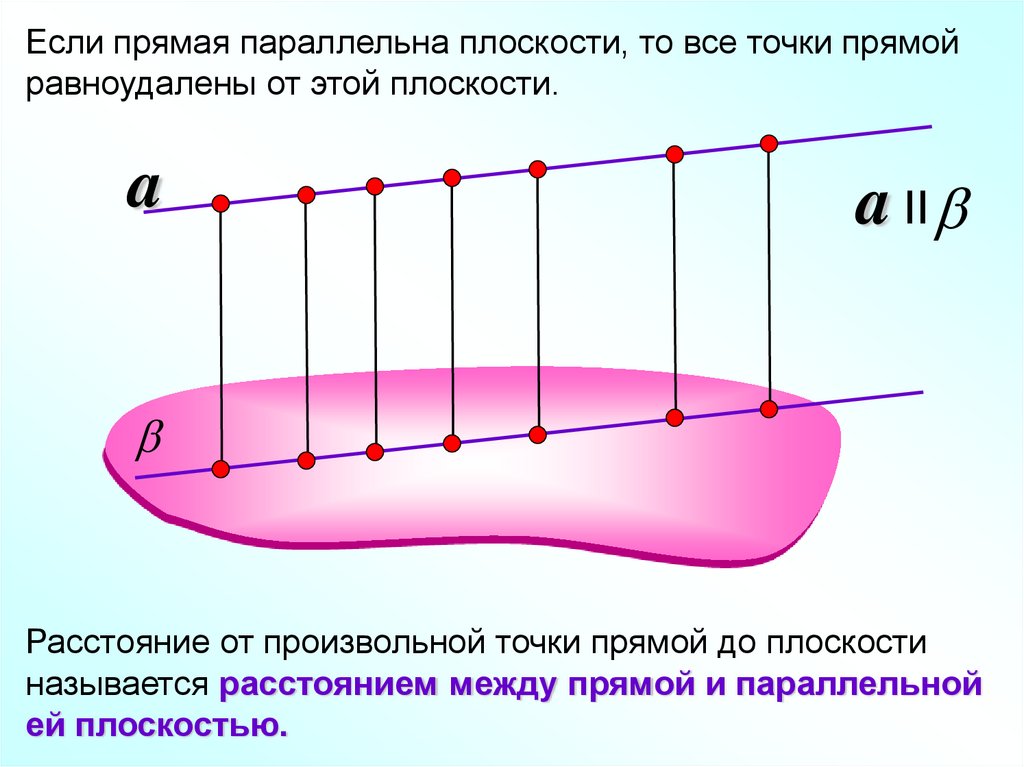
Если прямая параллельна плоскости, то все точки прямойравноудалены от этой плоскости.
a
a II
Расстояние от произвольной точки прямой до плоскости
называется расстоянием между прямой и параллельной
ей плоскостью.
11.
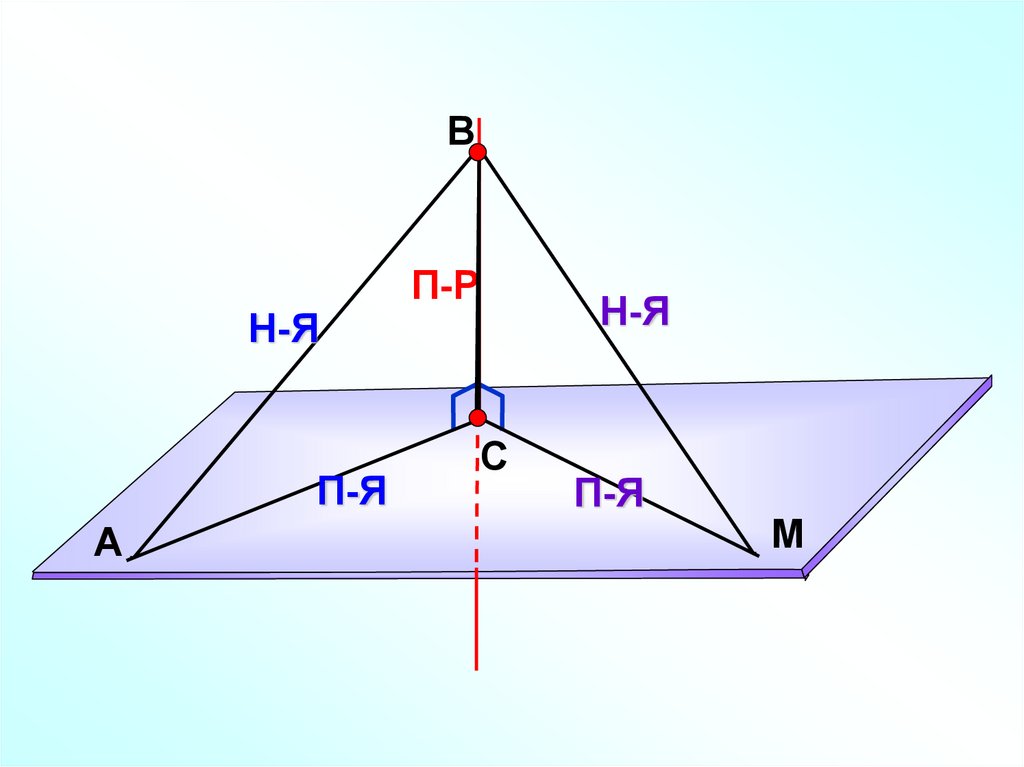
ВН-Я
П-Я
А
П-Р
С
Н-Я
П-Я
M
12.
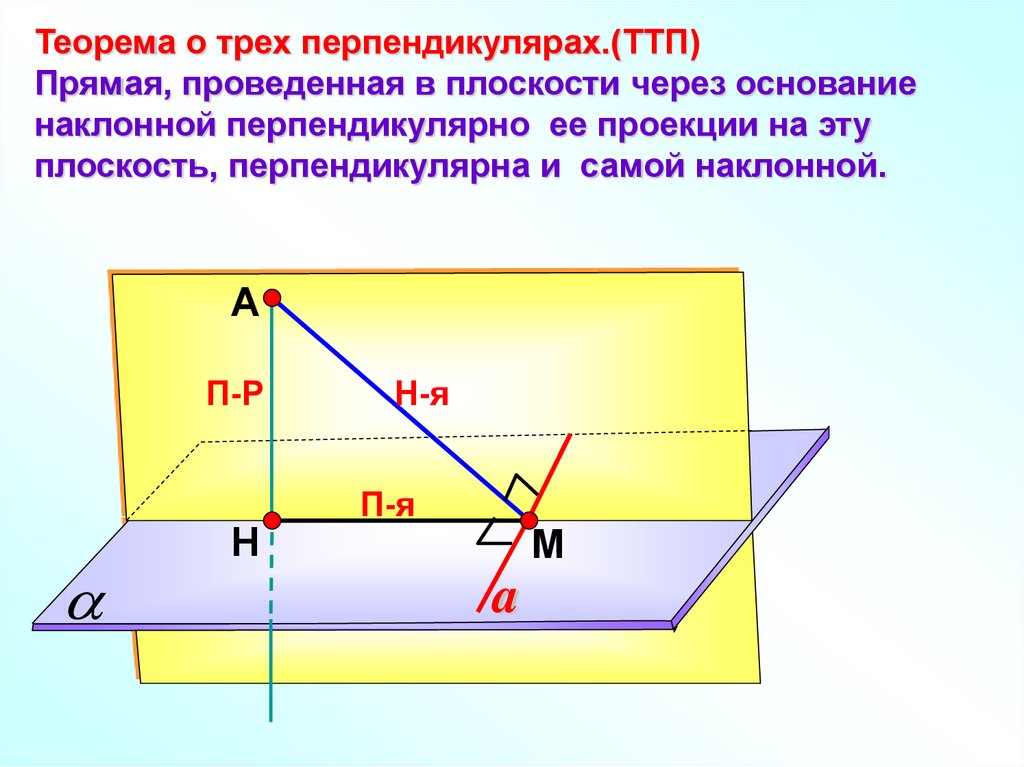
Теорема о трех перпендикулярах.(ТТП)Прямая, проведенная в плоскости через основание
наклонной перпендикулярно ее проекции на эту
плоскость, перпендикулярна и самой наклонной.
А
П-Р
Н
Н-я
П-я
М
a
13.
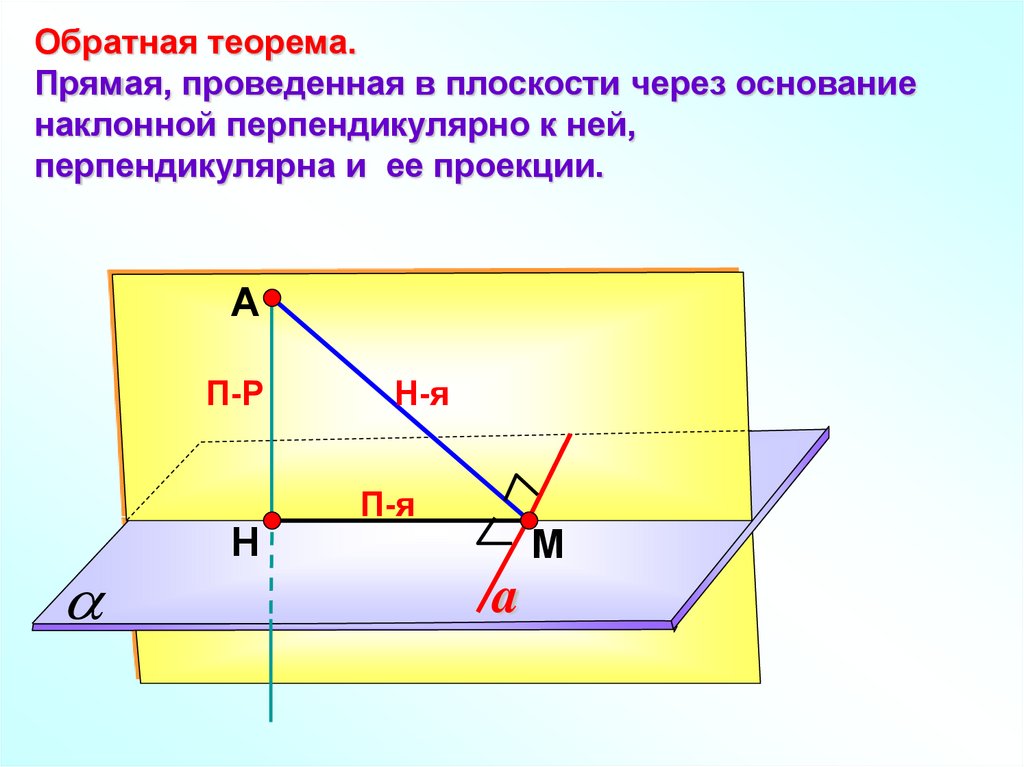
Обратная теорема.Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней,
перпендикулярна и ее проекции.
А
П-Р
Н
Н-я
П-я
М
a
14. Применение знаний в стандартной ситуации
15.
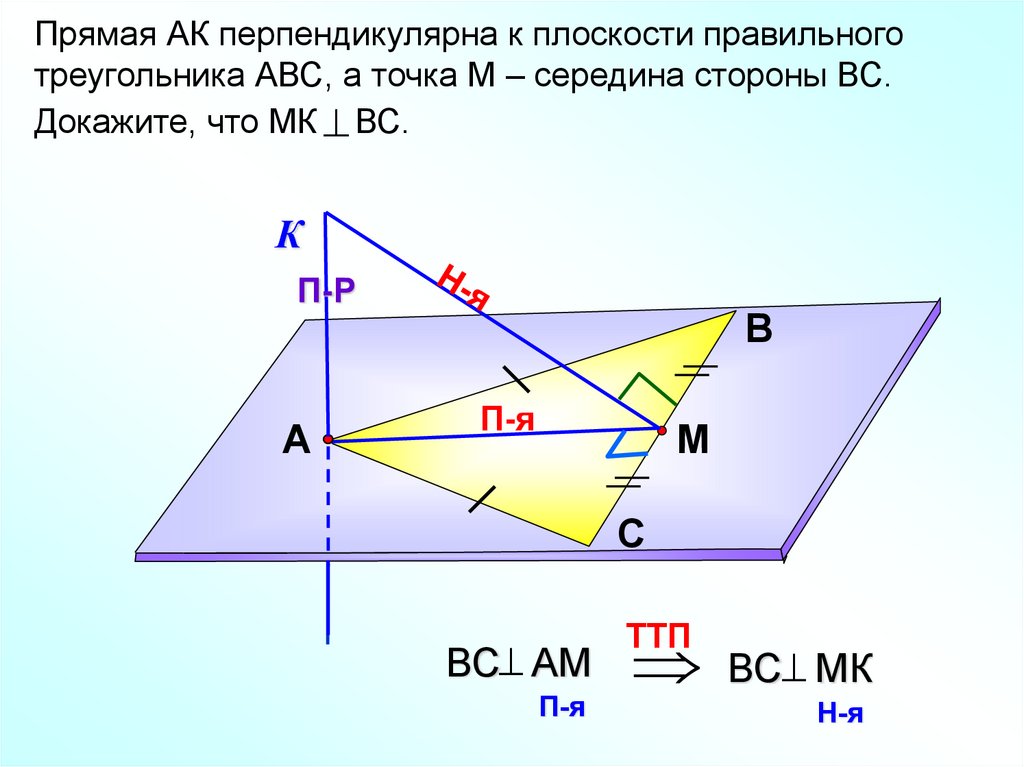
Прямая АК перпендикулярна к плоскости правильноготреугольника АВС, а точка М – середина стороны ВС.
Докажите, что МК ВС.
К
П-Р
А
В
П-я
М
С
BC AМ
П-я
TTП
BC MК
Н-я
16.
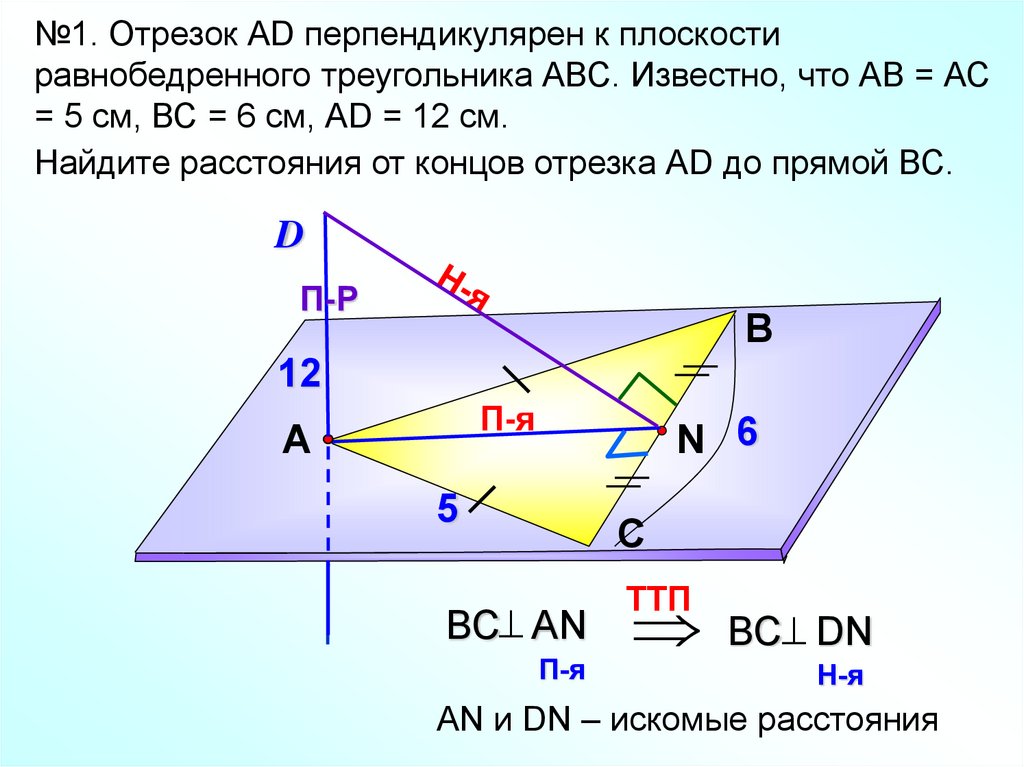
№1. Отрезок АD перпендикулярен к плоскостиравнобедренного треугольника АВС. Известно, что АВ = АС
= 5 см, ВС = 6 см, АD = 12 см.
Найдите расстояния от концов отрезка АD до прямой ВС.
D
П-Р
В
12
П-я
А
N 6
5
С
BC AN
П-я
TTП
BC DN
Н-я
АN и DN – искомые расстояния
17.
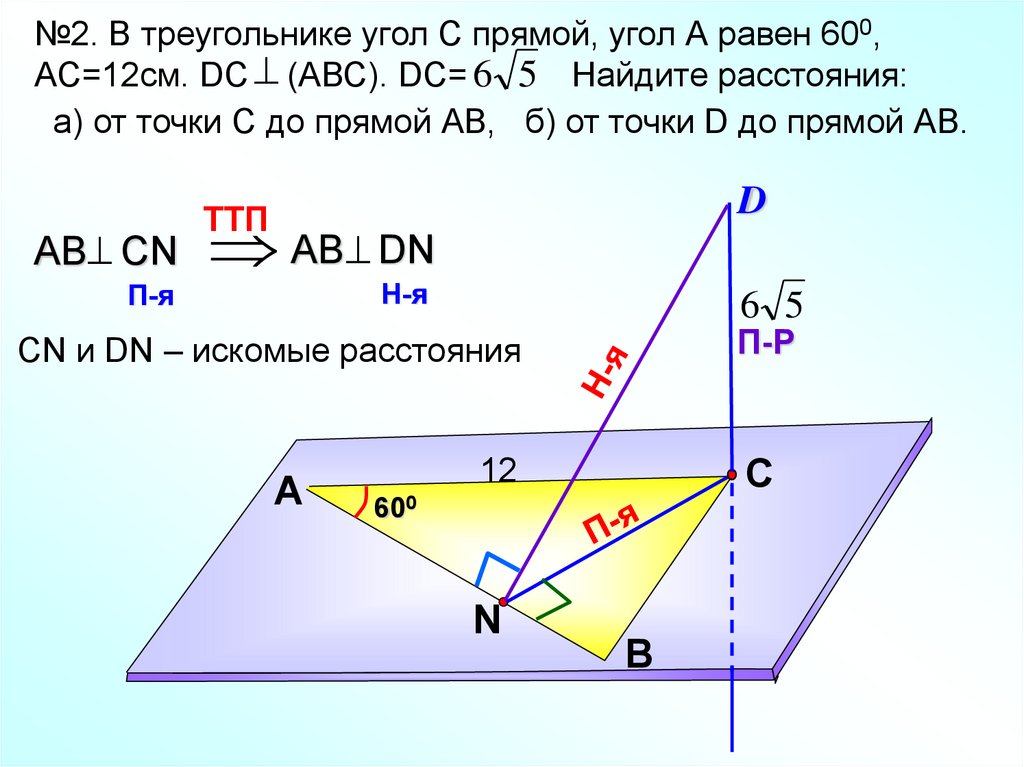
№2. В треугольнике угол С прямой, угол А равен 600,AС=12см. DC (АВС). DC= 6 5 Найдите расстояния:
а) от точки С до прямой АВ, б) от точки D до прямой АВ.
АВ СN
D
AB DN
TTП
Н-я
П-я
6 5
П-Р
CN и DN – искомые расстояния
А
С
12
600
N
В






 Математика
Математика








