Похожие презентации:
Средние величины
1.
2. § 1. ПОНЯТИЕ СРЕДНЕЙ ВЕЛИЧИНЫ
xСРЕДНЯЯ ВЕЛИЧИНА В
СТАТИСТИКЕ- ОБОБЩАЮЩИЙ
ПОКАЗАТЕЛЬ, ХАРАКТЕРИЗУЮЩИЙ
ТИПИЧНЫЙ УРОВЕНЬ ЯВЛЕНИЯ,
СВОДНАЯ ХАРАКТЕРИСТИКА
ЗАКОНОМЕРНОСТЕЙ ТОГО
ПРОЦЕССА, В КОТОРЫХ ОН
ПРОТЕКАЕТ.
3.
• Величины, в которых находят выражениеобщие условия, закономерность изучаемого
явления;
• Величины, отражающие то общее, что
складывается в каждом единичном объекте;
• Обобщённая количественная
характеристика признака в статистической
совокупности в конкретных условиях места и
времени;
• Является обобщением какого-то одного
свойства изучаемого явления или процесса.
4. Определяющее свойство средней
f ( x1 , x2 , x3 ,...,xn ) f ( x, x, x,...,x )Исходное соотношение средней (ИСС)
Суммарное значение осредняемого показателя
ИСС=
Количество единиц совокупности (объём)
5. ИСС для некоторых экономических показателей
Средняя ценареализованного=
товара
Стоимость реализованного товара
Средняя
себестоимость=
продукции
Затраты на производство продукции
Средняя
Заработная =
плата
Фонд заработной платы
Количество реализованного товара
Количество произведённой продукции
Количество работающих
Средний
Фактически достигнутый показатель
процент
=
выполнения плана
Запланированный показатель
6. ВИДЫ СРЕДНИХ ВЕЛИЧИН В СТАТИСТИКЕ
Средняя арифметическая (простая,взвешенная, средняя из групповых
средних);
Средняя гармоническая;
Средняя геометрическая;
Средняя степенная
(квадратическая, кубическая и т.д.);
Структурные средние.
7. § 2 СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА
8.
Используется длярасчёта среднего
значения признака
при известном
объёме совокупности
9.
nx
x
i
1
n
вычисляется, как сумма отдельных значений
признака (xi) делённая на их число (n)
Используется для расчёта среднего
значения признака при известных
индивидуальных значениях признака
(для несгруппированных данных)
10.
№квартиры
А
1
2
3
4
5
6
Итого
Задолженность по
оплате за
электроэнергию,
руб.
1
250
258
1234
180
194
706
2824
Найти задолженность по оплате за
электроэнергию в среднем на 1 квартиру
11.
Задолженность пооплате за
электроэнергию,
руб.
№
квартиры
А
1
2
3
4
5
6
Итого
x
1
250
258
1234
180
194
706
2824
n
x
1
n
i
Астафурова
470
,
67
руб
.
И.С.
12.
x fx
f
i
i
i
Вычисляется, если имеются многократные повторения
значения признака и совокупность разбита на группы,
используется для расчёта среднего значения
группировочного признака
(при сгруппированных данных)
13. РЯДЫ РАСПРЕДЕЛЕНИЯ
ИНТЕРВАЛЬНЫЙРЯД
ДИСКРЕТНЫЙ
РЯД
i
x
-середина
i- го интервала
xi -конкретное
значение
признака в i- й
f - численность i-ой группы (частота,
частость)
группе
i
14.
Если fi -численность группыn
f i
1 (100 %)
Если fi - доля (удельный) вес
группы
15.
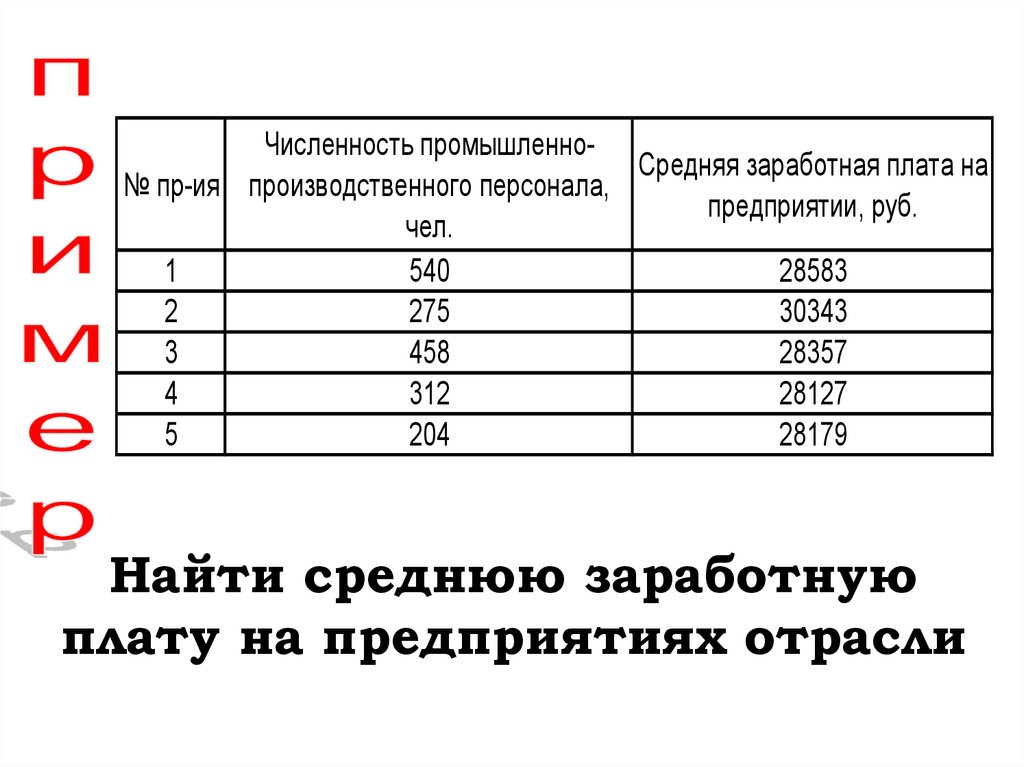
Численность промышленноСредняя заработная плата на№ пр-ия производственного персонала,
предприятии, руб.
чел.
1
540
28583
2
275
30343
3
458
28357
4
312
28127
5
204
28179
Найти среднюю заработную
плату на предприятиях отрасли
16.
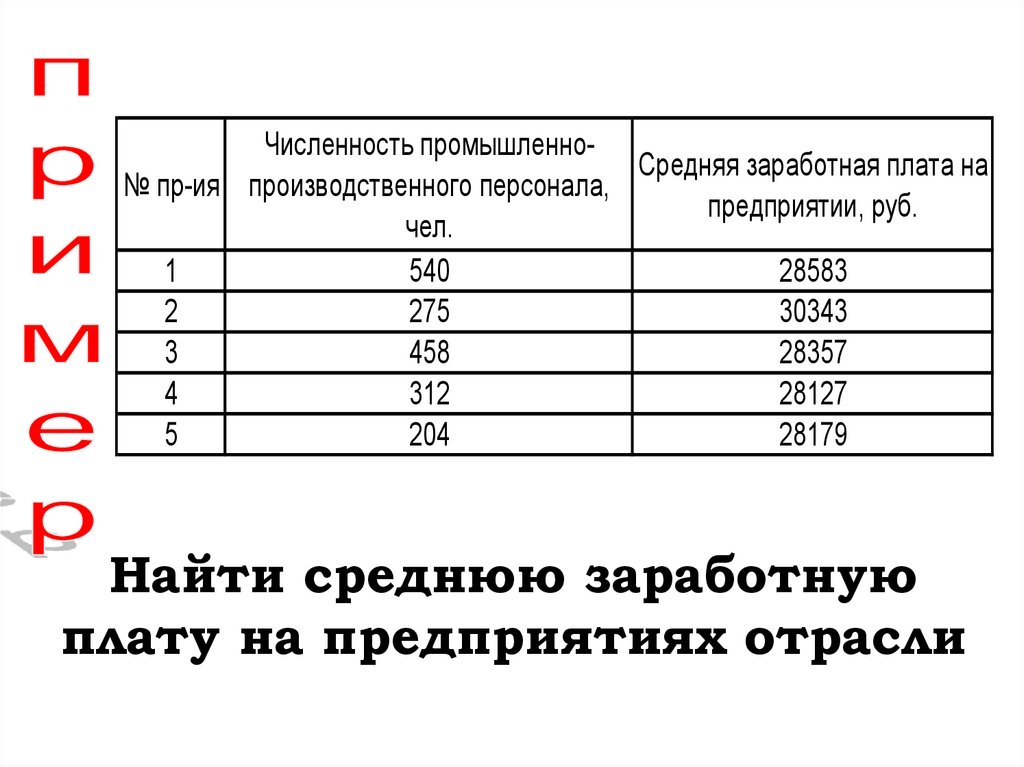
Численность промышленноСредняя заработная плата на№ пр-ия производственного персонала,
предприятии, руб.
чел.
1
540
28583
2
275
30343
3
458
28357
4
312
28127
5
204
28179
Найти среднюю заработную
плату на предприятиях отрасли
17.
№ пр-ия1
2
3
4
5
Итого:
Численность
промышленнопроизводственного
персонала, чел., f i
Средняя заработная
плата на
предприятии, руб.,
540
275
458
312
204
28583
30343
28357
28127
28179
1789
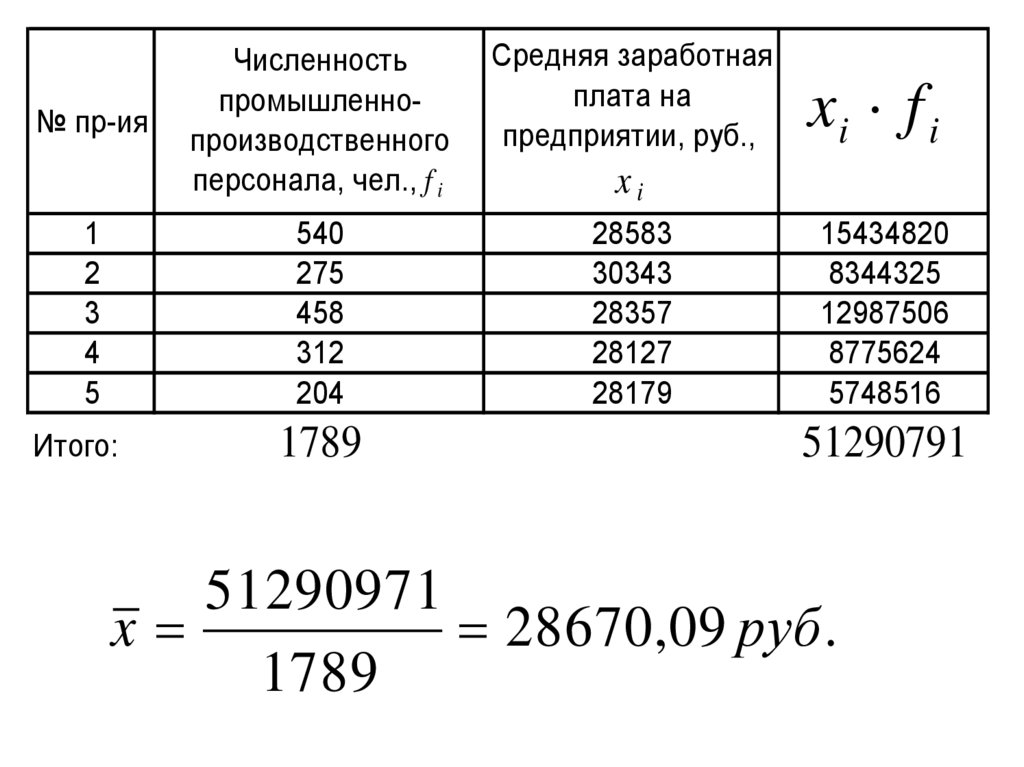
xi f i
xi
15434820
8344325
12987506
8775624
5748516
51290791
51290971
x
28670,09 руб .
1789
18.
kx
xi
1
k
Используется для расчёта среднего значения
результативного признака
( при сгруппированных данных)
19.
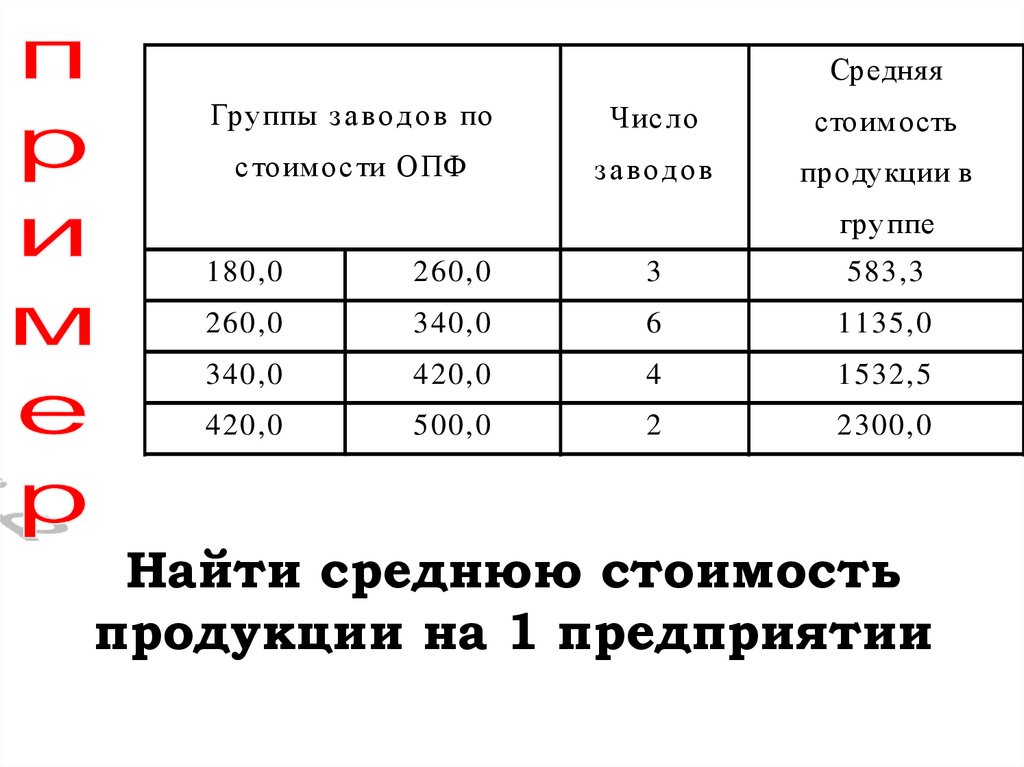
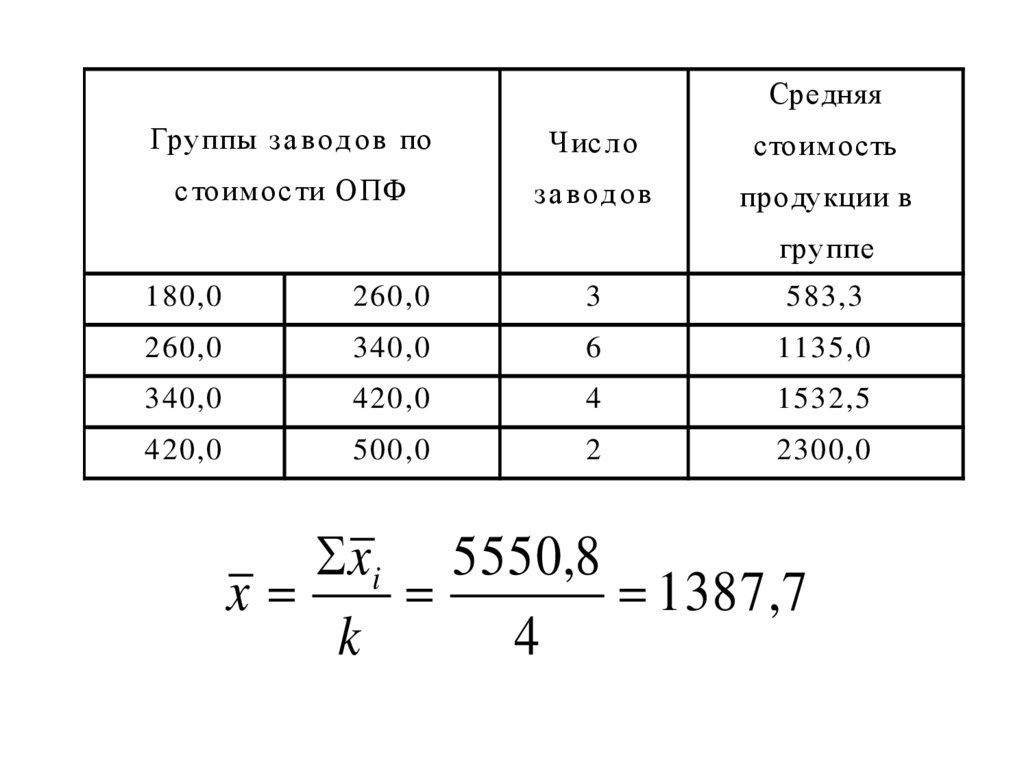
СредняяГруппы за в од ов по
Чис ло
стоим ость
с тоим ос ти ОПФ
за в од ов
продукции в
группе
180,0
260,0
3
583,3
260,0
340,0
6
1135,0
340,0
420,0
4
1532,5
420,0
500,0
2
2300,0
Найти среднюю стоимость
продукции на 1 предприятии
20.
СредняяГруппы за в од ов по
Чис ло
стоим ость
с тоим ос ти ОПФ
за в од ов
продукции в
группе
180,0
260,0
3
583,3
260,0
340,0
6
1135,0
340,0
420,0
4
1532,5
420,0
500,0
2
2300,0
xi 5550,8
x
1387 ,7
k
4
21. §3. СРЕДНЯЯ ГАРМОНИЧЕСКАЯ и другие виды средних величин
22.
Используетсяпри неизвестном объёме
совокупности или
необходимости обобщения
величины, обратной
изучаемому признаку.
23.
xn
1
x
n
1
i
несгруппированные
данные
24.
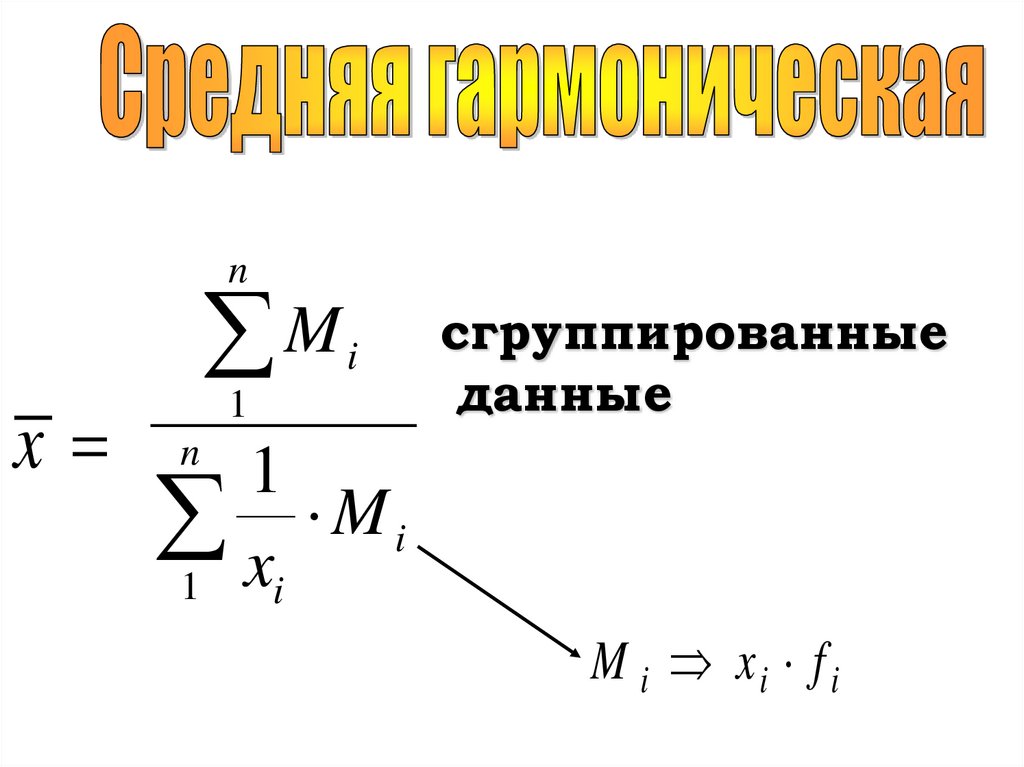
nx
M
i
1
сгруппированные
данные
n
1
1 x M i
i
M i xi f i
25.
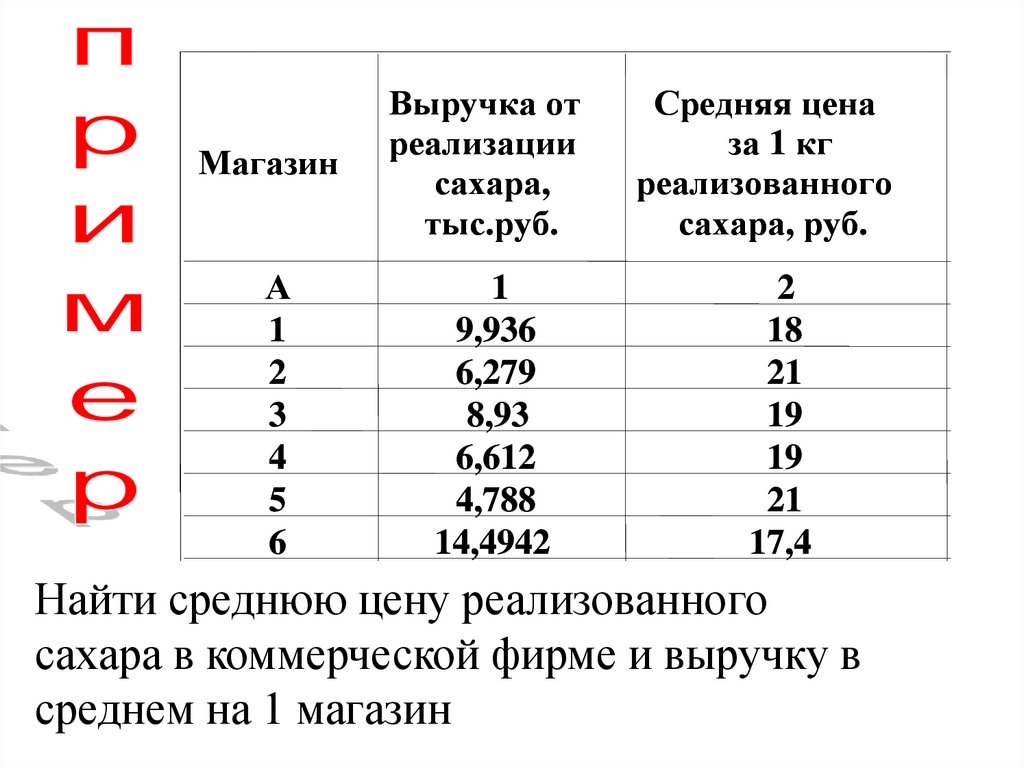
МагазинВыручка от
реализации
сахара,
тыс.руб.
А
1
2
3
4
5
6
1
9,936
6,279
8,93
6,612
4,788
14,4942
Средняя цена
за 1 кг
реализованного
сахара, руб.
2
18
21
19
19
21
17,4
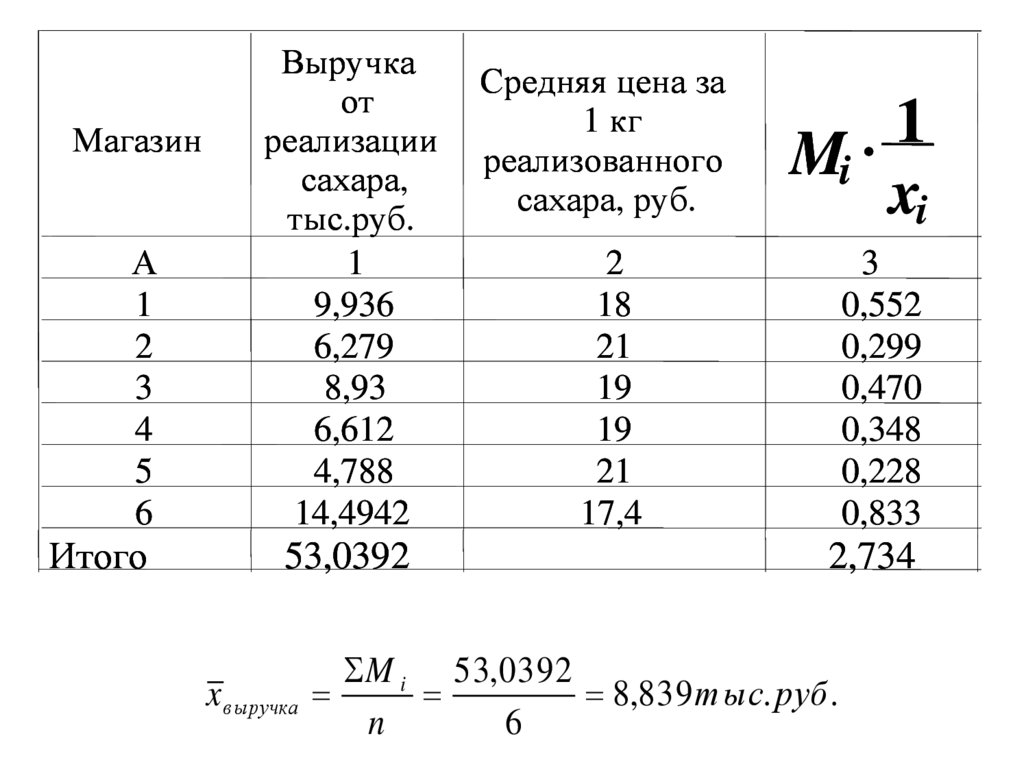
Найти среднюю цену реализованного
сахара в коммерческой фирме и выручку в
среднем на 1 магазин
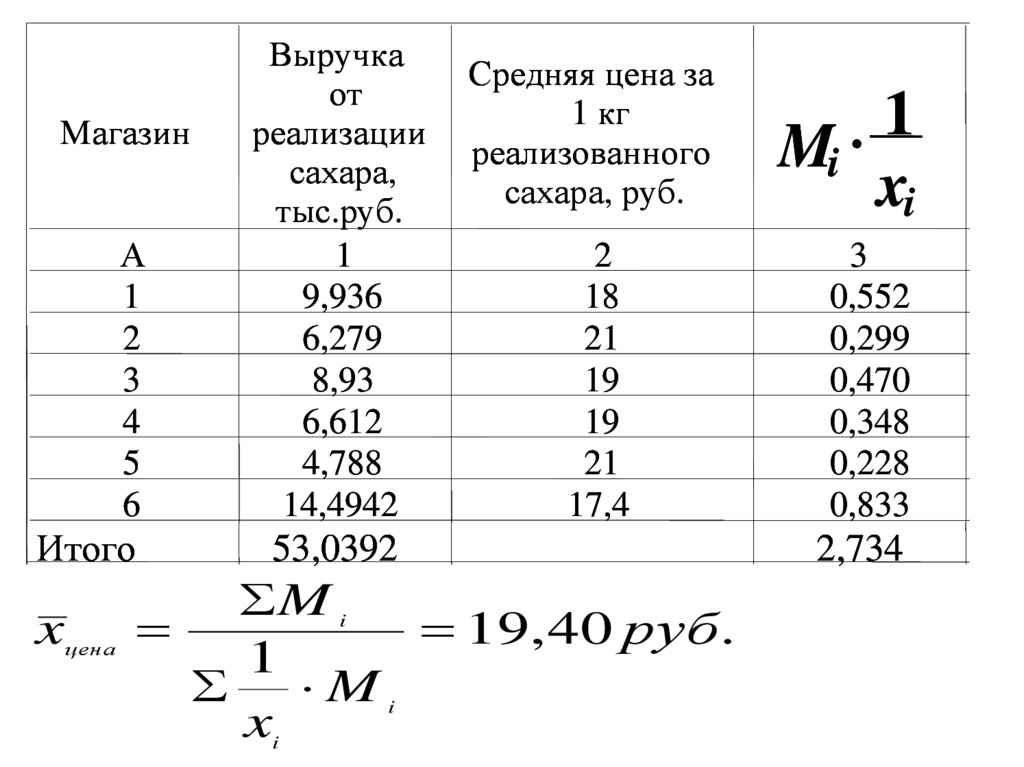
26.
МагазинА
1
2
3
4
5
6
Итого
x
Выручка
от
реализации
сахара,
тыс.руб.
1
9,936
6,279
8,93
6,612
4,788
14,4942
53,0392
2
18
21
19
19
21
17,4
M
19, 40 руб.
1
M
x
i
цена
Средняя цена за
1 кг
реализованного
сахара, руб.
i
i
1
Mi
xi
3
0,552
0,299
0,470
0,348
0,228
0,833
2,734
27.
МагазинА
1
2
3
4
5
6
Итого
Выручка
от
реализации
сахара,
тыс.руб.
1
9,936
6,279
8,93
6,612
4,788
14,4942
53,0392
x в ыручка
Средняя цена за
1 кг
реализованного
сахара, руб.
1
Mi
xi
2
18
21
19
19
21
17,4
3
0,552
0,299
0,470
0,348
0,228
0,833
2,734
M i 53,0392
8,839 тыс. руб .
n Астафурова
6 И.С.
28.
x x1 x2 x3 ... xnn
Используется для расчёта средних
темпов и коэффициентов роста
в рядах динамики
29. САМОСТОЯТЕЛЬНО:
• Построитьпоследовательность действий
по выбору формулы для
расчёта среднего значения
признака
30.
§ 4. СТРУКТУРНЫЕСРЕДНИЕ ВЕЛИЧИНЫ
31.
Астафурова И.С.32. Мо
•Мода (Мо) значение признаканаиболее часто
встречающееся в
вариационном ряду.
Астафурова И.С.
33. Ме
•Медиана (Ме) значение варьирующегопризнака, приходящееся
на середину ряда,
варианта, делящая ряд
на две равные части
Астафурова И.С.
34.
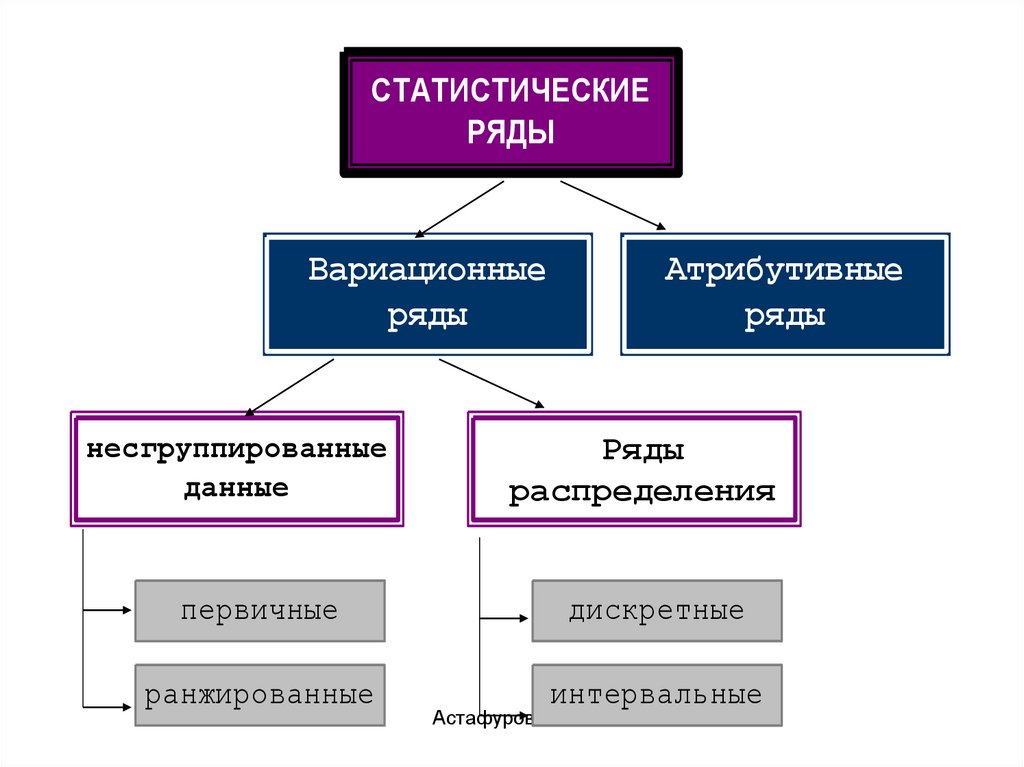
СТАТИСТИЧЕСКИЕРЯДЫ
Вариационные
ряды
несгруппированные
данные
Атрибутивные
ряды
сгруппированные
Ряды
данные
распределения
первичные
дискретные
ранжированные
интервальные
Астафурова И.С.
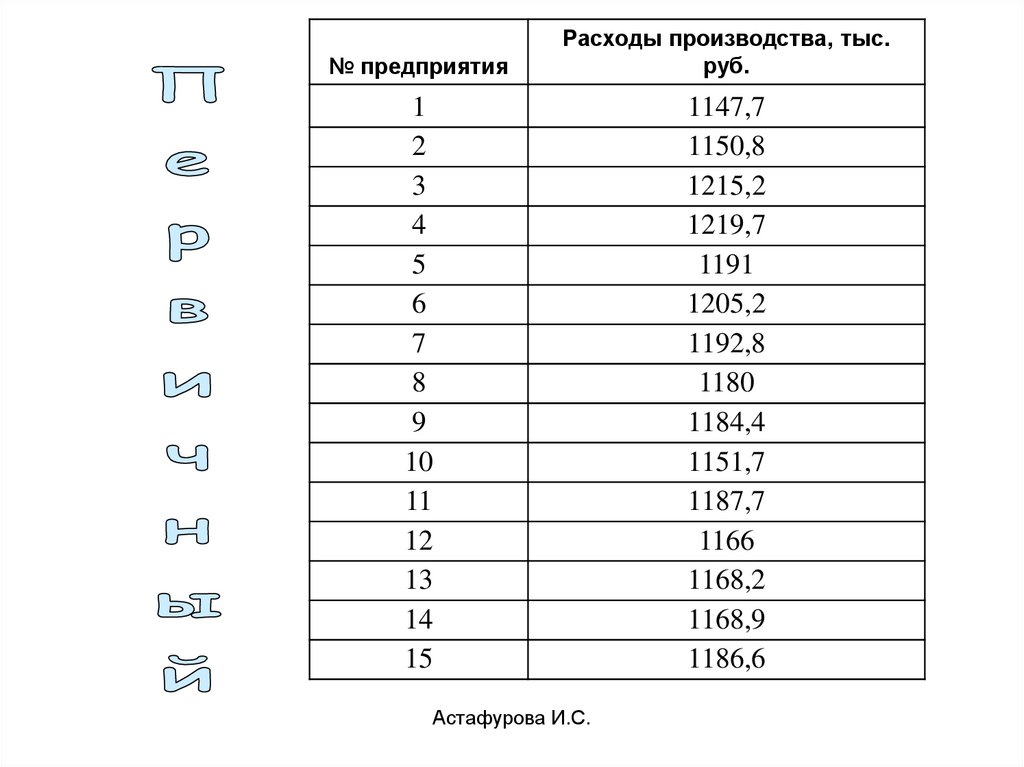
35. ПЕРВИЧНЫЙ РЯД
Моды и медианыпервичного ряда
не существует!
Астафурова И.С.
36.
№ предприятияРасходы производства, тыс.
руб.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1147,7
1150,8
1215,2
1219,7
1191
1205,2
1192,8
1180
1184,4
1151,7
1187,7
1166
1168,2
1168,9
1186,6
Астафурова И.С.
37. РАНЖИРОВАННЫЙ РЯД
Моды несуществует!
Астафурова И.С.
38. РАНЖИРОВАННЫЙ РЯД
Медиана - центральнаяварианта при нечетном
числе единиц
совокупности, при
четном числе она равна
полусумме серединных
вариант
Астафурова И.С.
39.
№ предприятия1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Расходы
производства,
тыс. руб.
1147,7
1150,8
1151,7
1166
1167,8
1168,2
1168,9
1180
1184,4
1186,6
1187,7
1191
1192,8
1205,2
1215,2
Астафурова И.С.
Mе 1180
40.
СТРУКТУРНЫЕ СРЕДНИЕДЛЯ СГРУППИРОВАННЫХ
ДАННЫХ
Определение:
Кумулятивная частота (Si)
результат суммирования
предшествующей кумулятивной частоты
с частотой текущей группы. Для
первой группы кумулятивная частота
равна частоте в группе.
S i S i 1 f i ,
где i изменяется от 1
Астафурова И.С.
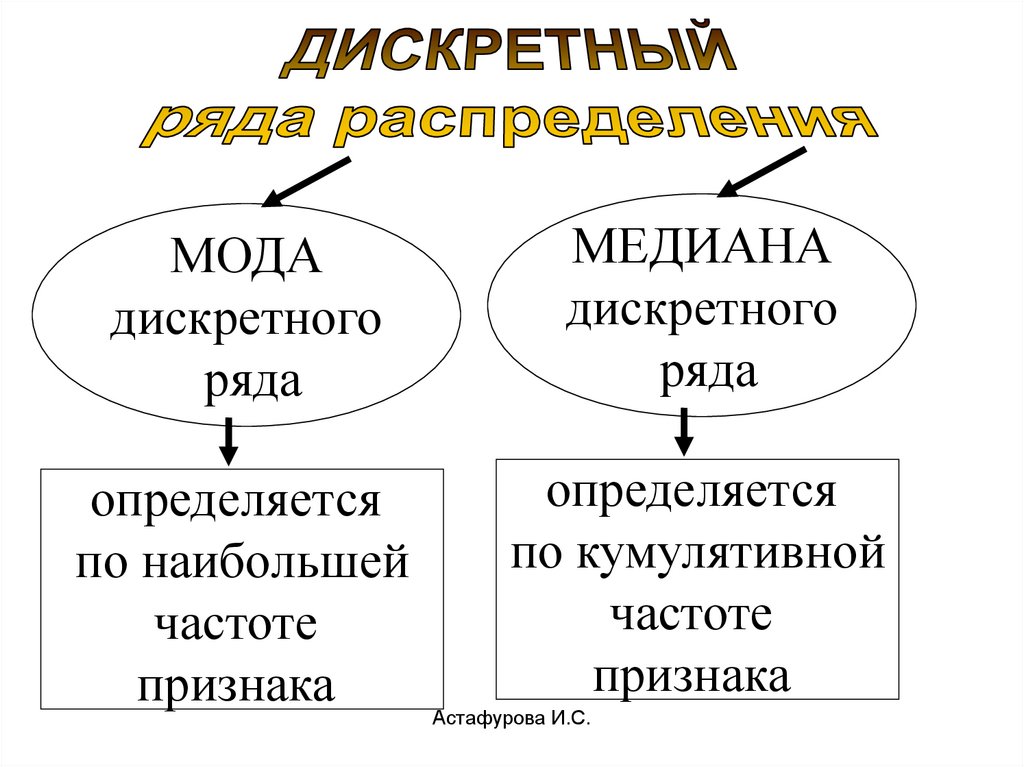
41.
МОДАдискретного
ряда
МЕДИАНА
дискретного
ряда
определяется
по наибольшей
частоте
признака
определяется
по кумулятивной
частоте
признака
Астафурова И.С.
42. ДИСКРЕТНЫЙ РЯД
Мода и медиана - конкретныеварианты
•Мода - варианта с максимальной
частотой,
•Медиана - варианта с с кумулятивной
частотой, превышающей полусумму
частот
f
S
2
Ме
i
Астафурова И.С.
43.
РазрядЧисло рабочих, чел.
1
15
2
27
3
32
4
40
5
14
6
2
Найти моду и медиану
дискретного ряда, сделать
выводы.
Астафурова И.С.
44.
ЧислоКумулятивная
Разряд рабочих,
частота, S i
чел.
1
15
15
2
27
42
3
32
74
4
40
114
5
14
128
6
2
130
130
Мо=4
Ме=3
Это означает, что большая часть
рабочих имеет 4 разряд.
Половина рабочих имеет разряд ниже 3,
а половина - выше.
Астафурова И.С.
45.
МОДА и МЕДИАНАопределяются по специальной
методике
Астафурова И.С.
46. ИНТЕРВАЛЬНЫЙ РЯД
•Определение 1•Модальный интервал - интервал с
максимальной частотой
•Определение 2
•Медианный интервал - интервал, у
которого кумулятивная частота не
менее полусуммы частот
f
S
2
Ме
i
47.
M o x Мof M o f M o 1
( f M o f M o 1 ) ( f M o f M o 1 )
Астафурова И.С.
hМo
48.
f iS M e 1
2
M e x Мe
hМe
fMe
Астафурова И.С.
49.
Величина доходов,тыс.руб.
10
20
20
30
30
40
40
50
50
60
60
70
Число
семей
152
211
304
207
36
11
Найти моду и медиану, сделать
выводы по результатам расчетов
Астафурова И.С.
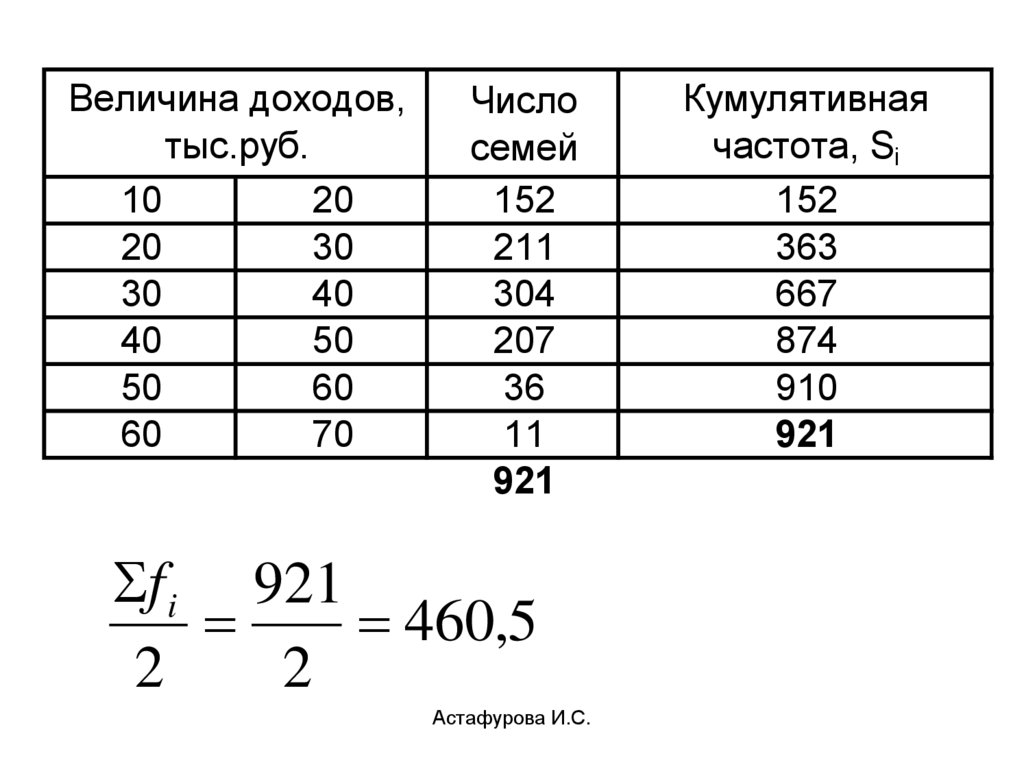
50.
Величина доходов,тыс.руб.
10
20
20
30
30
40
40
50
50
60
60
70
Число
семей
152
211
304
207
36
11
921
f i 921
460,5
2
2
Астафурова И.С.
Кумулятивная
частота, Si
152
363
667
874
910
921
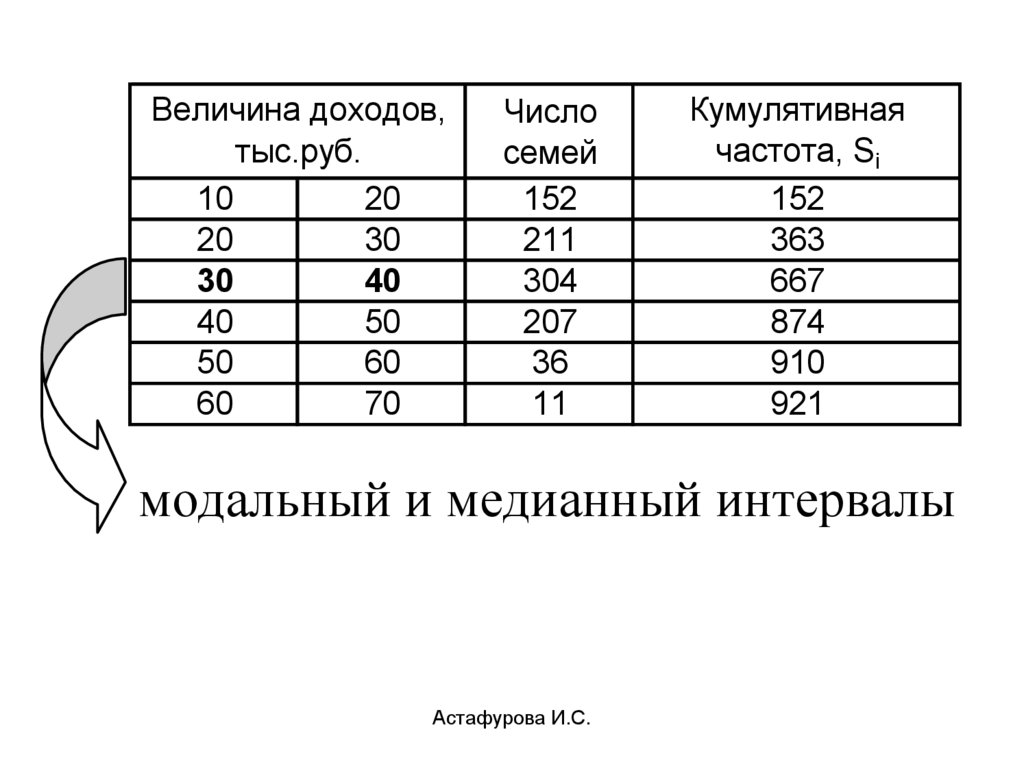
51.
Величина доходов,тыс.руб.
10
20
20
30
30
40
40
50
50
60
60
70
Число
семей
152
211
304
207
36
11
Кумулятивная
частота, Si
152
363
667
874
910
921
модальный и медианный интервалы
Астафурова И.С.
52.
304 211М о 30 (40 30)
(304 211) (304 207)
34,895 тыс.руб.
Большая часть семей имеет доход,
близкий к 34895 руб.
Астафурова И.С.
53.
460,5 363М е 30 (40 30)
304
40,321 тыс.руб.
Половина семей имеет величину
доходов менее 40321 руб., а половина
более 40321 руб.
Астафурова И.С.
54.
Выбор формулы для расчётасреднего значения признака
начинается с построения ИСС;
Основные виды средних величин в
статистике - средняя
арифметическая, средняя
гармоническая и средняя
геометрическая;
Окончательный выбор формулы
зависит от вида исходных данных.
Астафурова И.С.
55.
ВЫВОДЫ:Мода и медиана описывают структуру
совокупности по изучаемому признаку;
Для первичного ряда моды и медианы не
существует;
Для ранжированного ряда существует
только медиана;
Для дискретного ряда мода и медиана конкретные значения признака, для
интервального мода и медиана
рассчитываются по формулам.
Астафурова И.С.
56.
ЛекцияРЯДЫ
ДИНАМИКИ
57. § 1. ДИНАМИЧЕСКИЕ (ВРЕМЕННЫЕ) РЯДЫ, основные понятия и классификации
РЯДЫ ИЗМЕНЯЮЩИХСЯ ВО ВРЕМЕНИЗНАЧЕНИЙ СТАТИСТИЧЕСКОГО
ПОКАЗАТЕЛЯ, РАСПОЛОЖЕННЫХ В
ХРОНОЛОГИЧЕСКОМ ПОРЯДКЕ
ОПИСЫВАЮЩИХ РАЗВИТИЕ , ДВИЖЕНИЕ
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ
ПРОЦЕССОВ
yi – уровни в рядах динамики,
ti – показатели времени
Астафурова И.С.
58.
Сопоставимость рядовдинамики:
- по территории;
- по кругу охватываемых объектов;
- по единицам измерения;
- по времени регистрации;
- по ценам;
- по методологии расчёта
59. ЗАДАЧИ, РЕШАЕМЫЕ С ПОМОЩЬЮ РЯДОВ ДИНАМИКИ
Расчёт характеристик интенсивностиотдельных изменений в уровнях ряда от
периода к периоду, от даты к дате;
Определение общей закономерности на базе
средних показателей динамического ряда;
Выявление основных закономерностей
динамики исследуемого явления и факторов,
обуславливающих изменение изучаемого
объекта во времени;
Построение прогноза развития явления на
будущее.
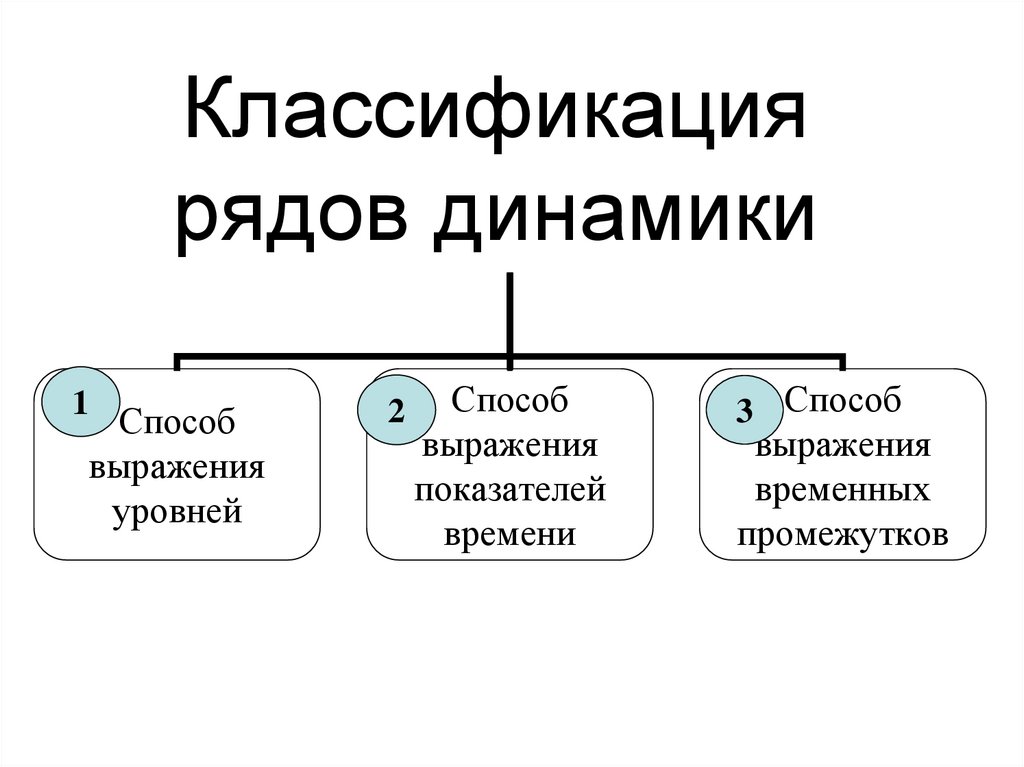
60. Классификация рядов динамики
1Способ
выражения
уровней
2
Способ
выражения
показателей
времени
3 Способ
выражения
временных
промежутков
61. Способ выражения уровней ряда динамики:
Составленный из абсолютныхвеличин;
Составленный из
относительных величин;
Составленный из средних
величин.
62. Способ выражения показателей времени ряда динамики:
Интервальный;Моментный.
63. Способ выражения временных промежутков ряда динамики:
С равноотстоящимиуровнями;
С неравноотстоящими
уровнями.
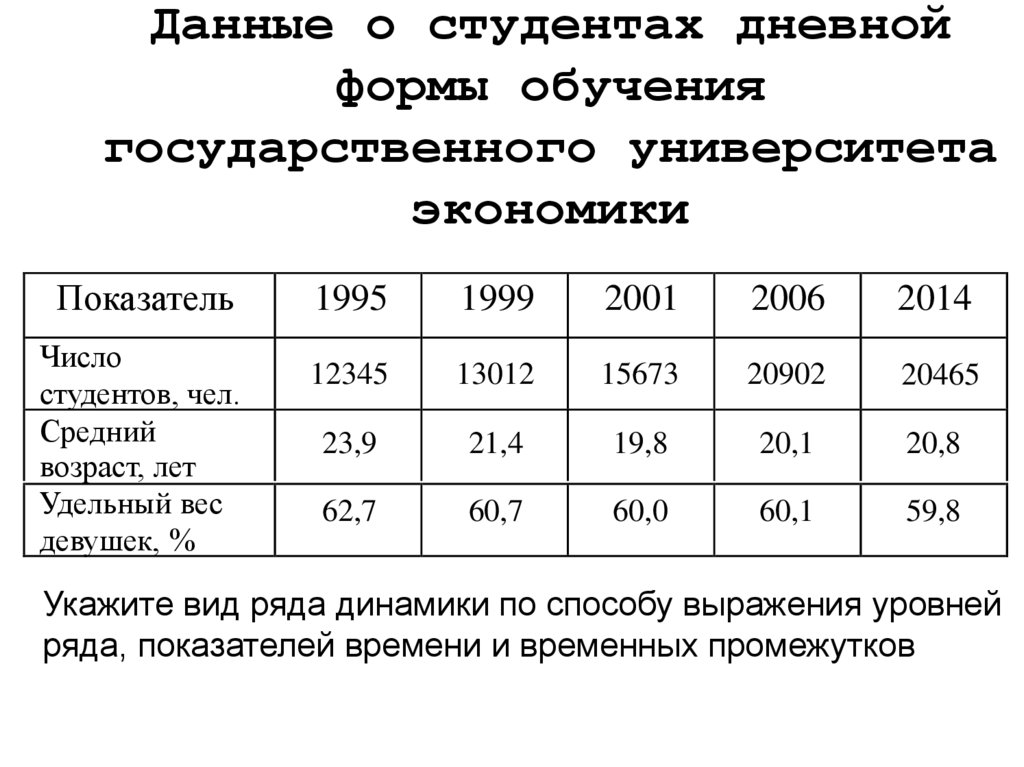
64. Данные о студентах дневной формы обучения государственного университета экономики
ПоказательЧисло
студентов, чел.
Средний
возраст, лет
Удельный вес
девушек, %
1995
1999
2001
2006
2014
12345
13012
15673
20902
20465
23,9
21,4
19,8
20,1
20,8
62,7
60,7
60,0
60,1
59,8
Укажите вид ряда динамики по способу выражения уровней
ряда, показателей времени и временных промежутков
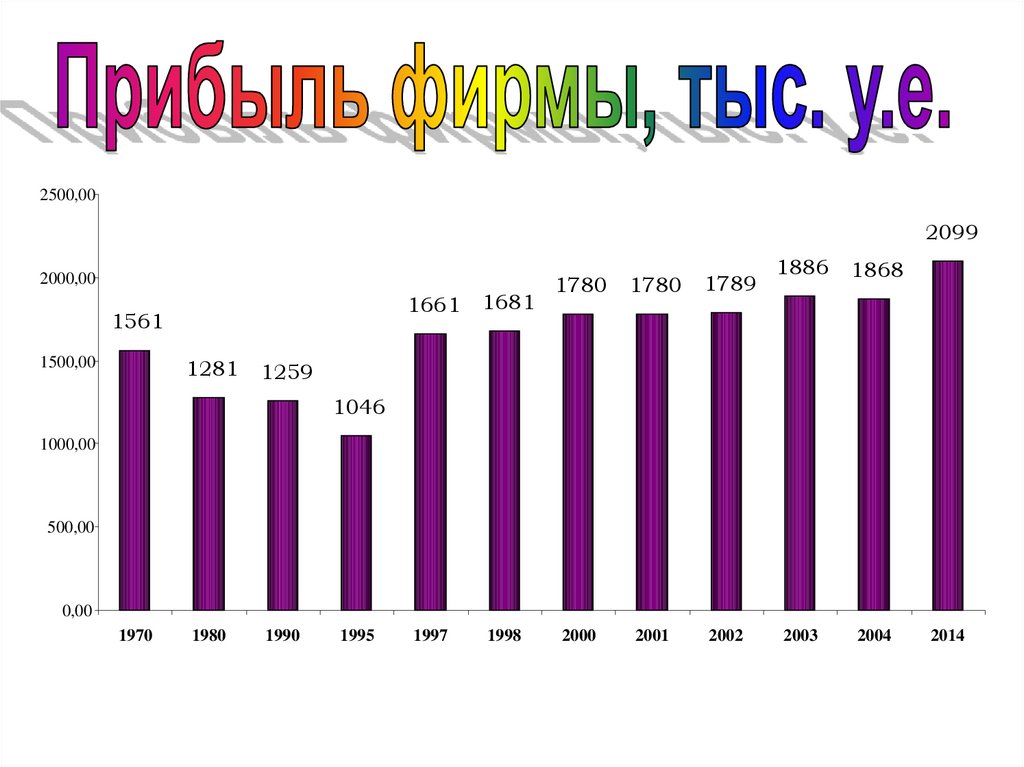
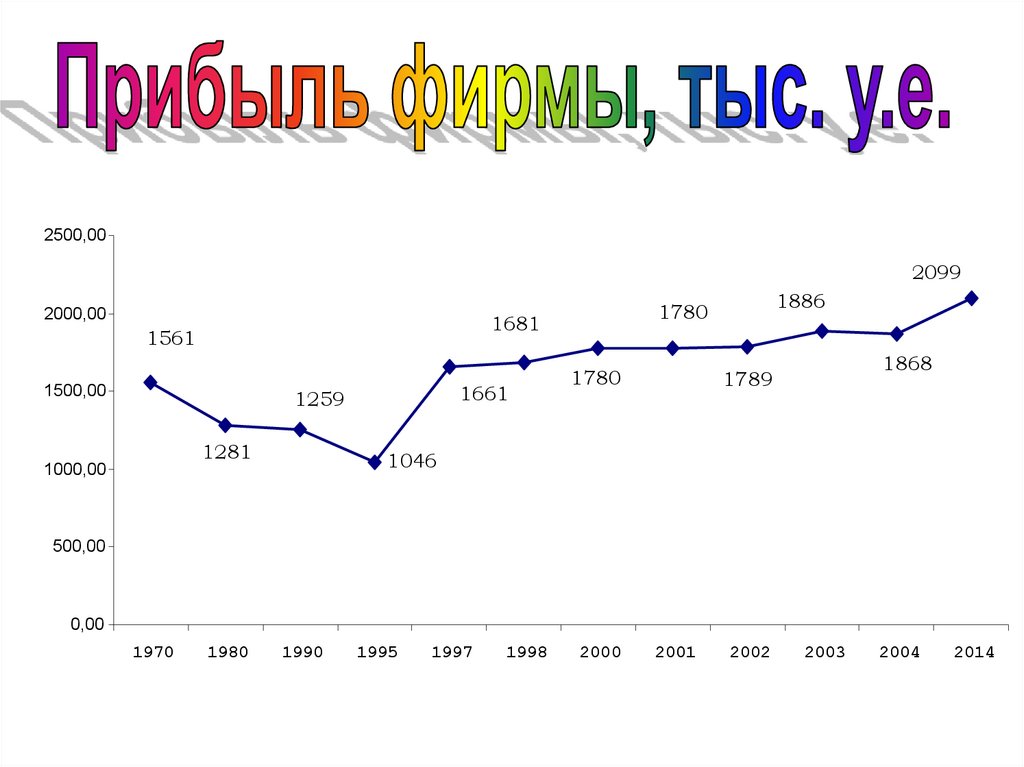
65. ПРИМЕРЫ ГРАФИЧЕСКОГО ИЗОБРАЖЕНИЯ ДИНАМИЧЕСКИХ РЯДОВ
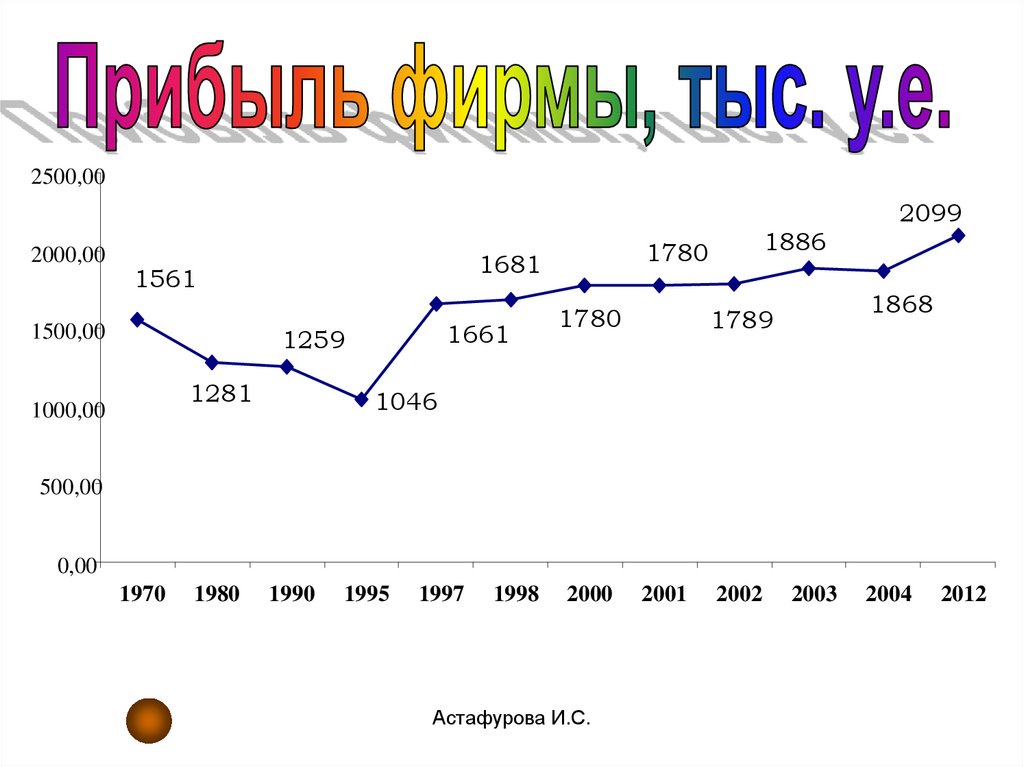
66.
2500,002099
2000,00
1661 1681
1561
1780 1780 1789
1886 1868
1281 1259
1500,00
1046
1000,00
500,00
0,00
1970
1980
1990
1995
1997
1998
2000
2001
2002
2003
2004
2014
67.
2500,002099
2000,00
1681
1561
1500,00
1661
1259
1281
1000,00
1886
1780
1780
1868
1789
1046
500,00
0,00
1970
1980
1990
1995
1997
1998
2000
2001
2002
2003
2004
2014
68. § 2. Характеристики рядов динамики
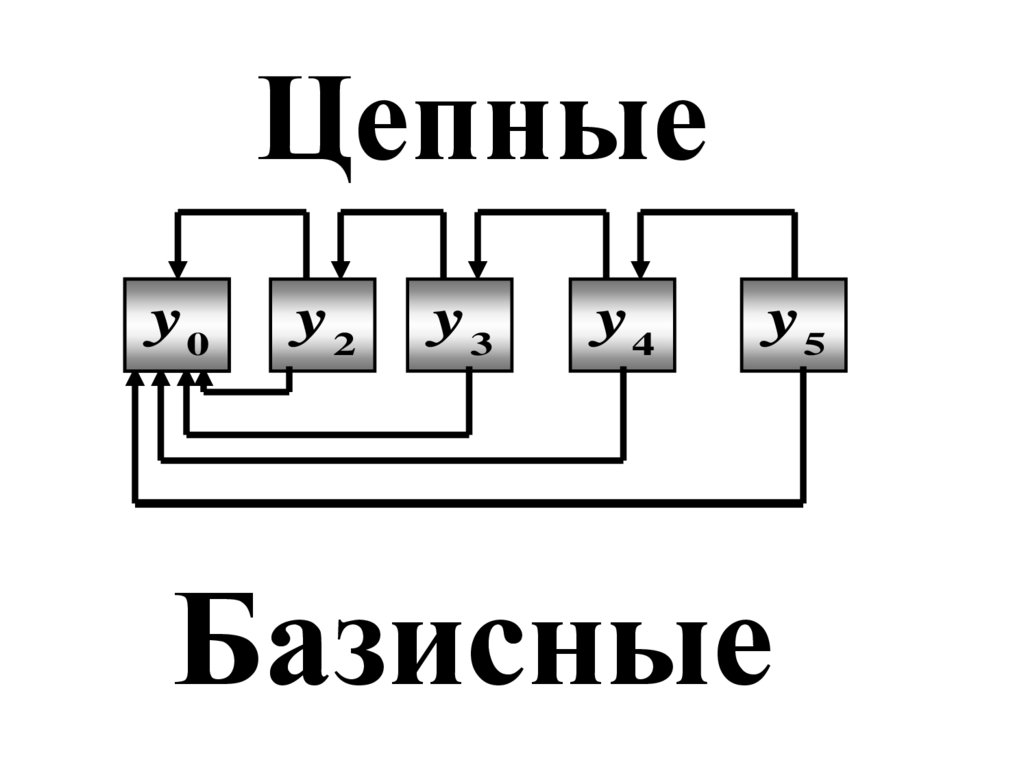
69.
Цепныеy10
y2
y3
y4
y5
Базисные
70.
Абсолютныйприрост
y i y i 1 цепной
i
y
y
базисный
i
0
71.
Коэффициентроста
Кi
yi
yi 1
yi
y0
цепной
базисный
72.
Темп ростаTi K i 100%
73.
Темп приростаi ( баз)
100% базисный
y0
Ti Ti 100%
i ( цеп) 100% цепной
yi 1
.
74.
Абсолютное значение1 % прироста
Ai
i (цеп)
Ti (цеп)
0,01 yi 1
75.
Цепные и базисные показатели рядов динамикиНазвание
показателя
Абсолютный
прирост
Темп и
коэффициент
роста
Расчетная формула
yi y0 базисный
i
yi yi 1 цепной
yi
y базисный
0
ki
y
i
цепной
yi 1
Ti ki 100%
Ti Ti 100%
Темп прироста
Абсолютное
значение 1 %
прироста
i ( баз)
100% базисный
y0
i (цеп) 100% цепной
yi 1
Ai
i (цеп)
Ti (цеп)
0,01 yi 1
Содержание
В абсолютных величинах отличие текущего
уровня от базисного или предыдущего
(приращение уровня ряда). Если
абсолютный прирост положителен, то
показатель увеличился, а если отрицателен –
уменьшился
В относительных величинах сравнение
текущего
уровня
с
базисным
или
предыдущим. Если коэффициент превышает
1 (темп роста 100%), то уровень увеличился,
а если менее 1 (темп роста менее 100%), то
уменьшился.
В относительных величинах отличие
текущего уровня от базисного или
предыдущего (на сколько процентов
произошел рост или снижение уровня ряда).
Показывает размер уровня ряда,
приходящегося на 1 % изменения (темпа
прироста).
76.
§ 3.СРЕДНИЕХАРАКТЕРИСТИКИ
i (цепные)
n 1
77.
§ 3.СРЕДНИЕХАРАКТЕРИСТИКИ
K
n 1
K 2 K 3 ... K n
T K 100%
78.
§ 3.СРЕДНИЕХАРАКТЕРИСТИКИ
T T 100 %
79.
yiy
n
Равноотстоящие
уровни
80.
yi tiy
ti
Неравноотстоящие
уровни
Астафурова И.С.
81.
y1 y nyi
2
2
y
n 1
n 1
Равноотстоящие
уровни
Астафурова И.С.
82.
y( y1 y 2 ) t1 ... ( y n 1 y n ) t n 1
2 (t1 t 2 t 3 ... t n 1 )
Неравноотстоящие
уровни
Астафурова И.С.
83.
ny
(y
i 1
yi ) ti 1
1
n
2 ti 1
1
Неравноотстоящие
уровни
Астафурова И.С.
84. § 4. МЕТОДЫ СГЛАЖИВАНИЯ РЯДОВ ДИНАМИКИ
ГРАФИКУКРУПНЕНИЕ ИНТЕРВАЛОВ
СКОЛЬЗЯЩЕЙ СРЕДНЕЙ
АНАЛИТИЧЕСКОГО
ВЫРАВНИВАНИЯ
Астафурова И.С.
85.
800700
2500,00
600
500
2000,00
400
1681
1561
1500,00
300
1000,00
1661
1259
1281
1780
1780
1886
1789
2099
1868
1046
200
500,00
100
0
0,00
1970
1995
1980
1990 1997
1995 1997
1998 2000
2002 2003
2012
1996
1998
199920012000
20012004 2002
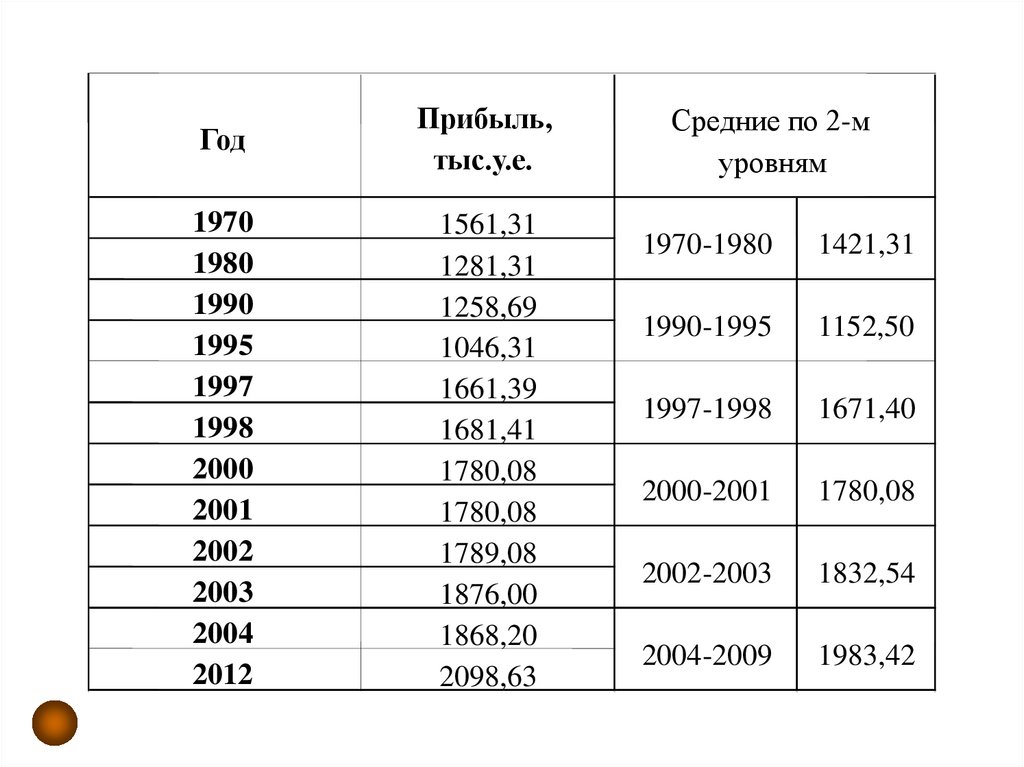
86.
ГодПрибыль,
тыс.у.е.
1970
1980
1990
1995
1997
1998
2000
2001
2002
2003
2004
2012
1561,31
1281,31
1258,69
1046,31
1661,39
1681,41
1780,08
1780,08
1789,08
1876,00
1868,20
2098,63
Средние по 2-м
уровням
1970-1980
1421,31
1990-1995
1152,50
1997-1998
1671,40
2000-2001
1780,08
2002-2003
1832,54
2004-2009
1983,42
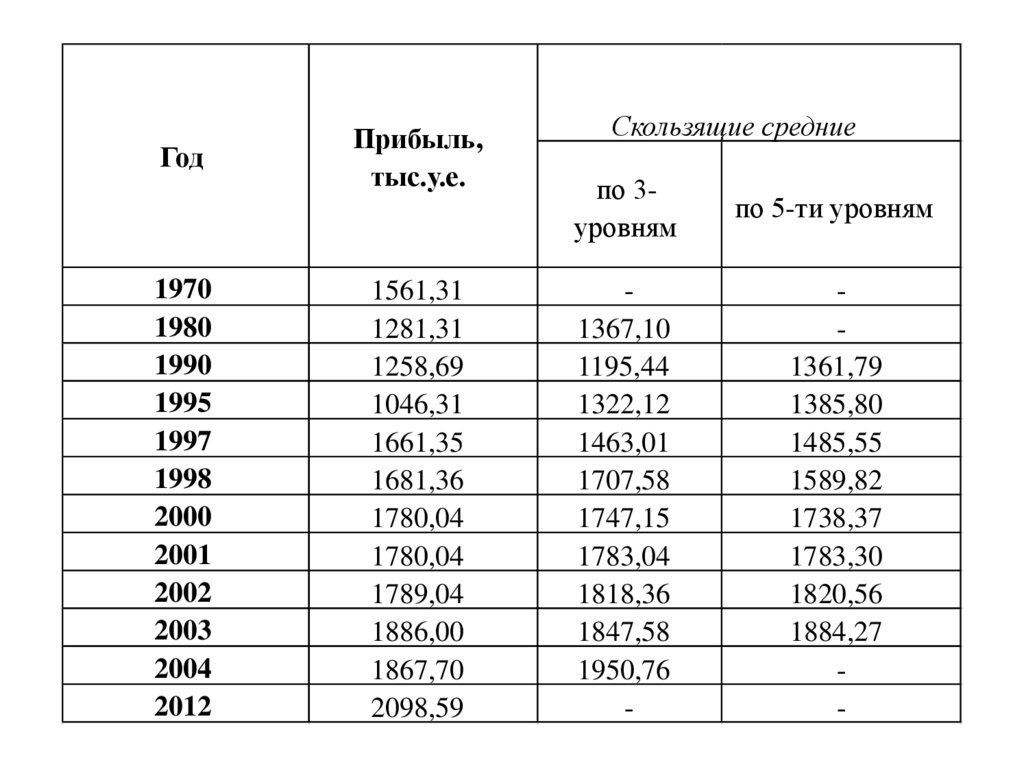
87.
Год1970
1980
1990
1995
1997
1998
2000
2001
2002
2003
2004
2012
Прибыль,
тыс.у.е.
1561,31
1281,31
1258,69
1046,31
1661,35
1681,36
1780,04
1780,04
1789,04
1886,00
1867,70
2098,59
Скользящие средние
по 3уровням
по 5-ти уровням
1367,10
1195,44
1322,12
1463,01
1707,58
1747,15
1783,04
1818,36
1847,58
1950,76
-
1361,79
1385,80
1485,55
1589,82
1738,37
1783,30
1820,56
1884,27
-
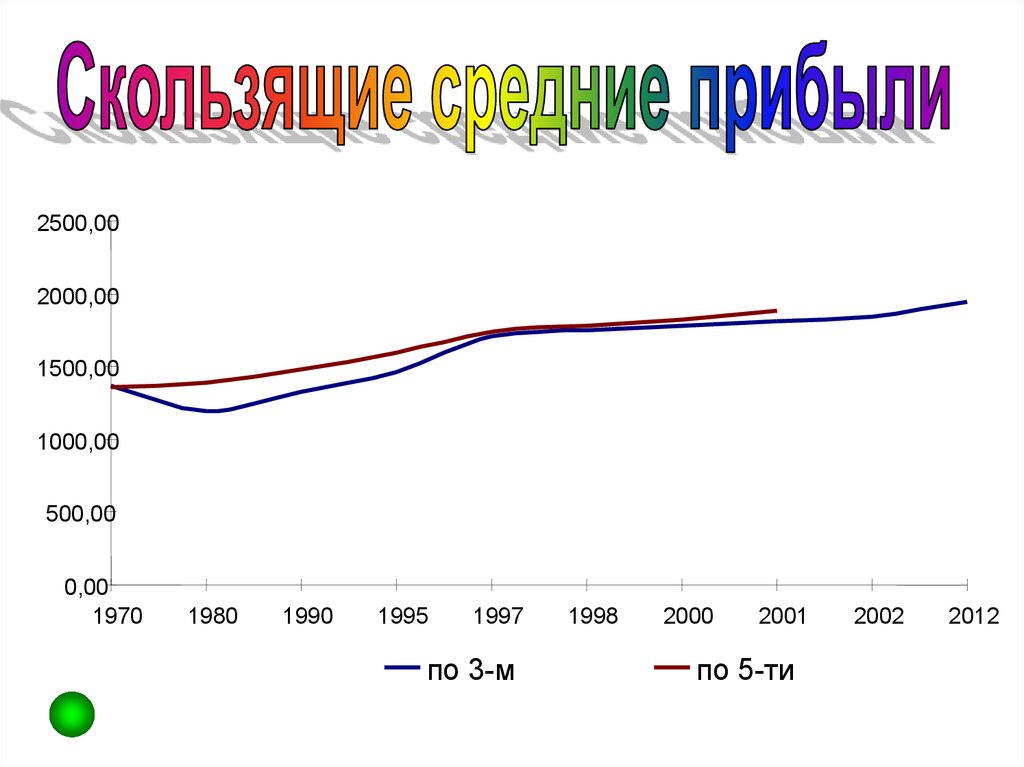
88.
6002500,00
400
2000,00
300
1500,00
200
1000,00
100
500,00
00,00
1970
1996
1980
19961990
1995
19971997
по 3-м
1998
1998 2000
2001
1999 2002
по 5-ти
2001
2012
89. Аналитическое выравнивание
способ выявления основной тенденциизакономерности развития, представляет
собой подбор функции времени
yˆ t f ( t )
где ŷt теоретические уровни
динамического ряда, рассчитанные на
основе адекватной математической
модели
Астафурова И.С.
90.
Основная тенденцияразвития (тренд) –
плавное и устойчивое
изменение уровня
явления во времени,
свободное от случайных
колебаний
Астафурова И.С.
91. Алгоритм построения прогноза на основе тренда
• Графическое изображение ряда ввиде линейной диаграммы
• Выбор тренда (аналитического
выражения зависимости от
показателя времени)
• Расчёт параметров тренда, его
оценка
• Экстраполяция уровней в прошлое
(ретроспектива) и в будущее
(перспектива) не более 1/3
изучаемого периода
Астафурова И.С.
92.
800700
2500,00
600
2000,00
500
1500,00
1661
1259
400
1281
1000,00
1886
1780
1681
1561
1780
2099
1868
1789
1046
300
500,00
200
1000,00
0
1970
1995
1980
1990
1996
1995
1997
1997
1998
1998
2000
1999
Астафурова И.С.
2001
2002
2000
2003
2004
2001
2012
93.
Простейшиевиды трендов
и т.д.
Астафурова И.С.
94.
Астафурова И.С.95.
Линейный трендŷt a b t
a
n
b
t
y
i
i
2
a ti b ti yi ti
ti
2 k 1
0
Астафурова И.С.
96.
S ŷty
S ŷt
100%
( yi ŷt (
расч )
n m
6%
Астафурова И.С.
2
)
97.
Параболический трендŷt a b t c t
2
a n b t i c t i y i
2
3
a t i b t i c t i y i t i
2
3
4
2
a
t
b
t
c
t
y
t
i
i
i
i i
6%
2
Астафурова И.С.
98. Построение расчёта
Экстраполяция - нахождениеуровней за пределами
изучаемого ряда;
Экстраполяция на период не
превышающий 1/3 изучаемого.
Астафурова И.С.
99. Построение расчёта
yˆ t f (ti ) в уравнение трендаставят значение
ti
соответствующее
расчётному периоду
Астафурова И.С.
,
100. Задание значений условным ti
n 8 ti 7 ; 5 ; 3; 1;1;3;5 ;7n 7 ti 3; 2 ; 1;0 ;1;2 ;3;
ŷt
- при подстановке соответствующего значения t
получаем точечный прогноз
Астафурова И.С.
101. Построение доверительного интервала прогноза на основе тренда
yˆ t t S yˆt yпрогноз yˆ t t S yˆtS yˆ t
( yi yˆ t ( расч) )
n m
Астафурова И.С.
2
102. Построение доверительного интервала прогноза на основе тренда
tКоэффициент доверия по таблице
распределения Стьюдента в зависимости от
числа степеней свободы (n-m) и значения
(вероятность наступления нежелательного
события)
1 p
Астафурова И.С.
103. ПРИМЕР
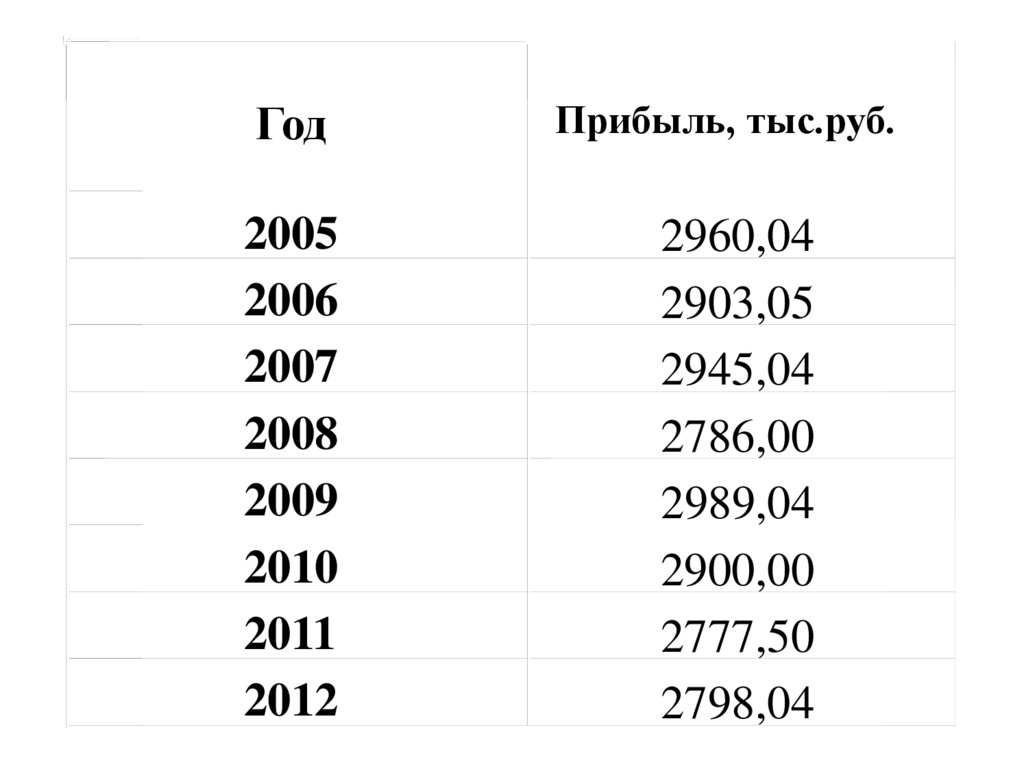
Астафурова И.С.104.
Год2005
2006
2007
2008
2009
2010
2011
2012
Прибыль, тыс.руб.
Астафурова И.С.
2960,04
2903,05
2945,04
2786,00
2989,04
2900,00
2777,50
2798,04
105.
ЗАДАНИЕ1.Рассчитать:
- характеристики ряда;
- средние характеристики ряда;
2.Построить тренд, спрогнозировать
прибыль на 2014 г., построить
доверительный интервал прогноза с
вероятностью 0,99.
3. Сделать выводы.
Астафурова И.С.
106.
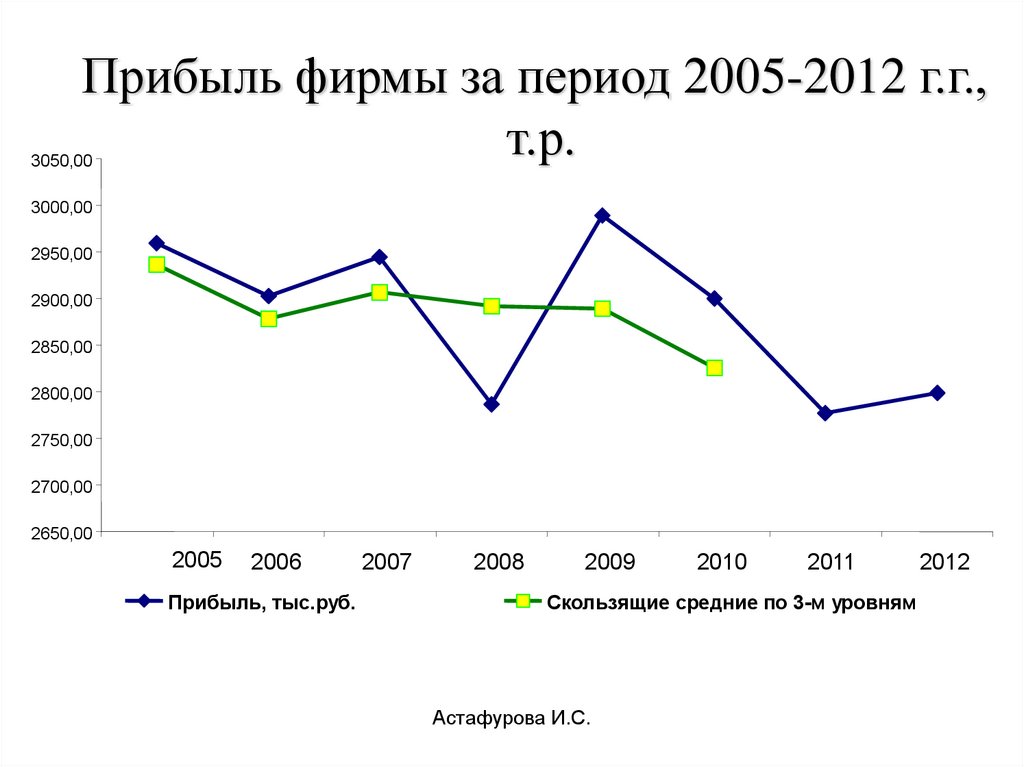
Прибыль фирмы за период 2005-2012 г.г.,т.р.
3050,00
3000,00
2950,00
2900,00
2850,00
2800,00
2750,00
2700,00
2650,00
2005
2006
Прибыль, тыс.руб.
2007
2008
2009
2010
2011
Скользящие средние по 3-м уровням
Астафурова И.С.
2012
107.
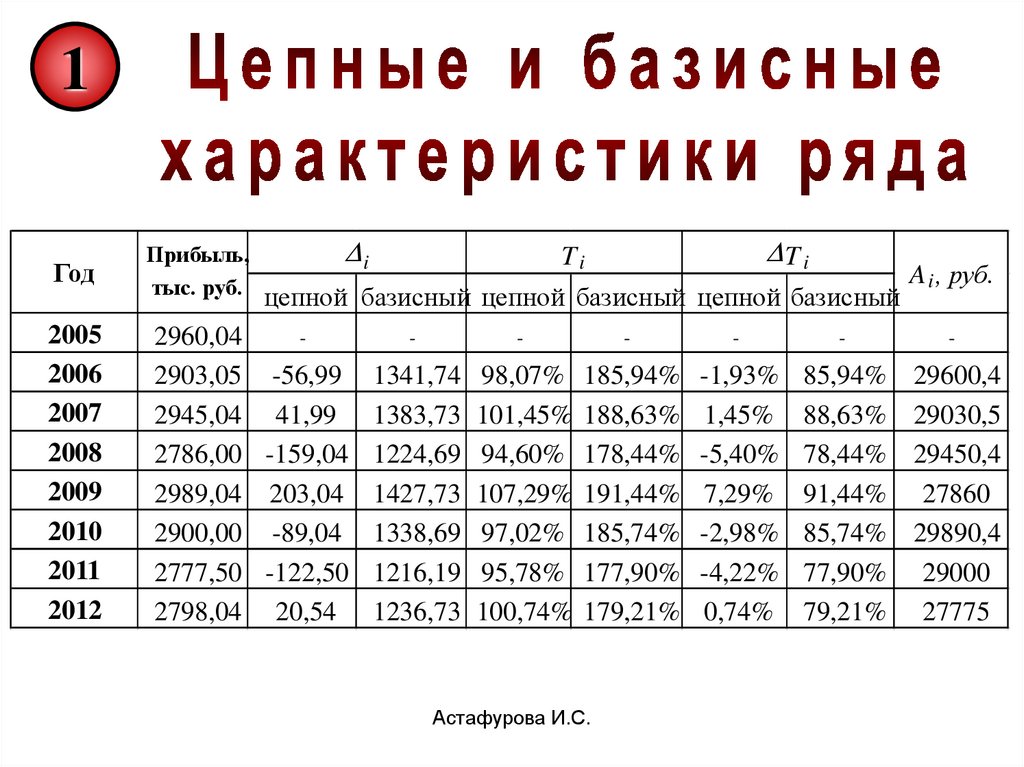
1Год
2005
2006
2007
2008
2009
2010
2011
2012
i
T i
Прибыль,
Ti
A , руб.
тыс. руб. цепной базисный цепной базисный цепной базисный i
2960,04
2903,05 -56,99 1341,74 98,07% 185,94% -1,93%
2945,04 41,99 1383,73 101,45% 188,63% 1,45%
2786,00 -159,04 1224,69 94,60% 178,44% -5,40%
2989,04 203,04 1427,73 107,29% 191,44% 7,29%
2900,00 -89,04 1338,69 97,02% 185,74% -2,98%
2777,50 -122,50 1216,19 95,78% 177,90% -4,22%
2798,04 20,54 1236,73 100,74% 179,21% 0,74%
Астафурова И.С.
-
-
85,94%
88,63%
78,44%
91,44%
85,74%
77,90%
79,21%
29600,4
29030,5
29450,4
27860
29890,4
29000
27775
108.
1i ( цепные)
162
23,143
7
n 1
T 7 98,07 101,45 94,60 107,29 97,02 95,78 100,74
99,2%;
ΔT 0,8%
yi
2882,34тыс. руб.
y
n
y2014 2798,04 2 ( 23,143) 2751,75тыс. руб.
Астафурова И.С.
109.
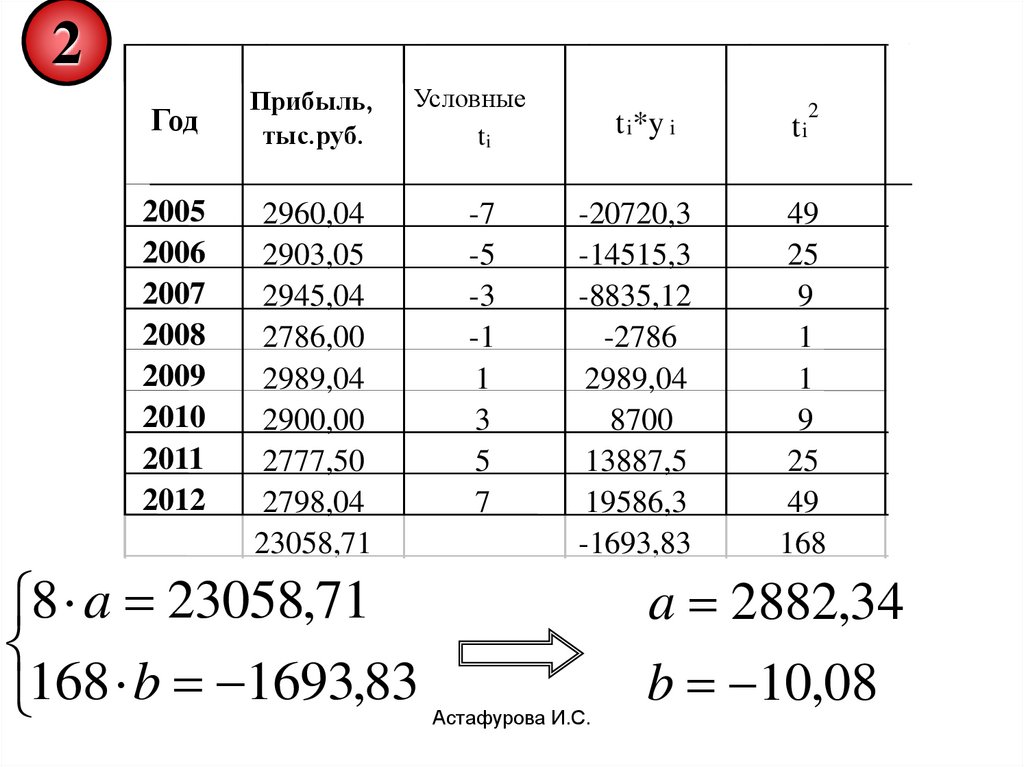
2Год
2005
2006
2007
2008
2009
2010
2011
2012
Прибыль,
тыс.руб.
Условные
ti
2960,04
2903,05
2945,04
2786,00
2989,04
2900,00
2777,50
2798,04
23058,71
8 a 23058,71
168 b 1693,83
-7
-5
-3
-1
1
3
5
7
t i*y i
-20720,3
-14515,3
-8835,12
-2786
2989,04
8700
13887,5
19586,3
-1693,83
ti
2
49
25
9
1
1
9
25
49
168
a 2882,34
Астафурова И.С.
b 10,08
110.
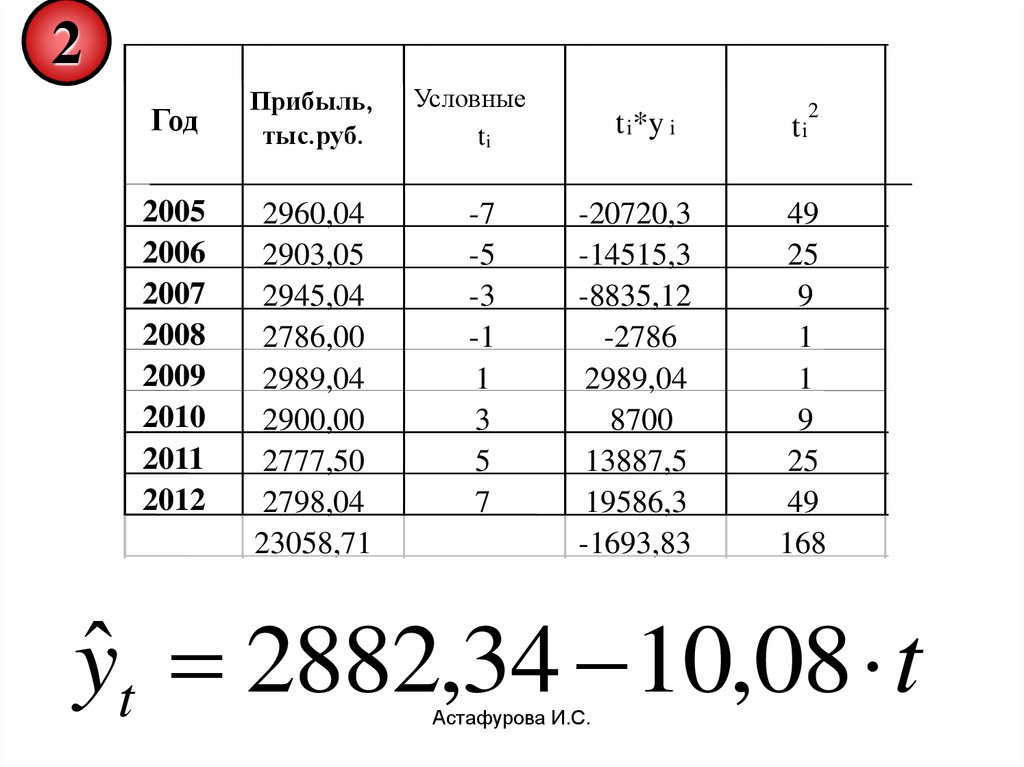
2Год
2005
2006
2007
2008
2009
2010
2011
2012
Прибыль,
тыс.руб.
2960,04
2903,05
2945,04
2786,00
2989,04
2900,00
2777,50
2798,04
23058,71
Условные
ti
-7
-5
-3
-1
1
3
5
7
t i*y i
-20720,3
-14515,3
-8835,12
-2786
2989,04
8700
13887,5
19586,3
-1693,83
ti
2
49
25
9
1
1
9
25
49
168
yˆ t 2882,34 10,08 t
Астафурова И.С.
111.
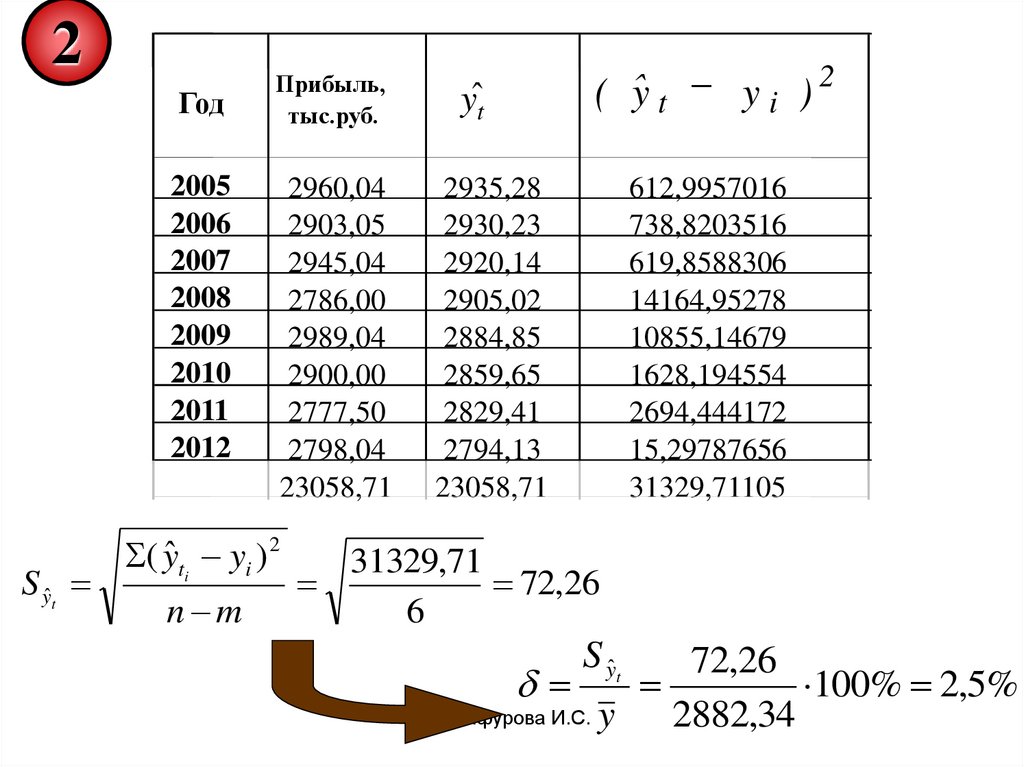
2Год
2005
2006
2007
2008
2009
2010
2011
2012
S yˆt
Прибыль,
тыс.руб.
2960,04
2903,05
2945,04
2786,00
2989,04
2900,00
2777,50
2798,04
23058,71
( yˆ ti yi ) 2
n m
yˆt
( ŷ t y i ) 2
2935,28
2930,23
2920,14
2905,02
2884,85
2859,65
2829,41
2794,13
23058,71
612,9957016
738,8203516
619,8588306
14164,95278
10855,14679
1628,194554
2694,444172
15,29787656
31329,71105
31329,71
72,26
6
S yˆt
72,26
100% 2,5%
Астафурова И.С. y
2882,34
112. Прогноз прибыли на основе тренда на 2014 г.
yˆ t 2882,34 10,08 tyˆ 2014 2784 ,66 т ыс. руб .
Астафурова И.С.
113. Доверительный интервал прогноза прибыли с вероятностью 0,99
yˆ 2014 2784 ,66 т ыс. руб .t 3,71; S 72,26
yˆ
2784,66 72,26 3,71 yˆ 2784,66 72,26 3,71
t
2516,58 yˆ 3052,75
t
Астафурова И.С.
114.
Астафурова И.С.115.
Динамические ряды позволяют изучать развитиеявления во времени с помощью абсолютных и
относительных показателей;
Абсолютные характеристики: абсолютное
значение 1 % прироста, абсолютный прирост,
средний абсолютный прирост, средний уровень
ряда;
Относительные характеристики: коэффициент,
темп роста и прироста, средние коэффициент,
темп роста и прироста;
С помощью тренда осуществляется прогноз на
будущее (перспективу) и расчёт уровня в
прошлом (ретроспектива);
Тренд отображает основную тенденцию развития
явления во времени, если сумма расчётных
уровней совпадает с суммой фактических
уровней, а ошибка тренда близка к 6 %.
Астафурова И.С.
116.
Астафурова И.С.117.
1Астафурова И.С.
118.
2n
y
i
ti
1
n
t
1
i
Астафурова И.С.
119.
3Ai
i ( цепной)
Ti ( цепной)
Астафурова И.С.
120.
4Астафурова И.С.
121.
5Астафурова И.С.
122.
6Какими бывают
ряды динамики
по способу
выражения
показателей
времени?
Астафурова И.С.
123.
7Астафурова И.С.
124.
8Какая формула для расчета
среднего уровня ряда используется:
1.1.09
Численность
работников, чел.
7
1.2.09
9
1.4.09
11
1.8.09
13
1.10.09
15
Дата
Астафурова И.С.
125.
9Астафурова И.С.
126.
10Какие характеристики
в рядах динамики
показывают общую
тенденцию изменений
в уровнях ряда?
Астафурова И.С.


































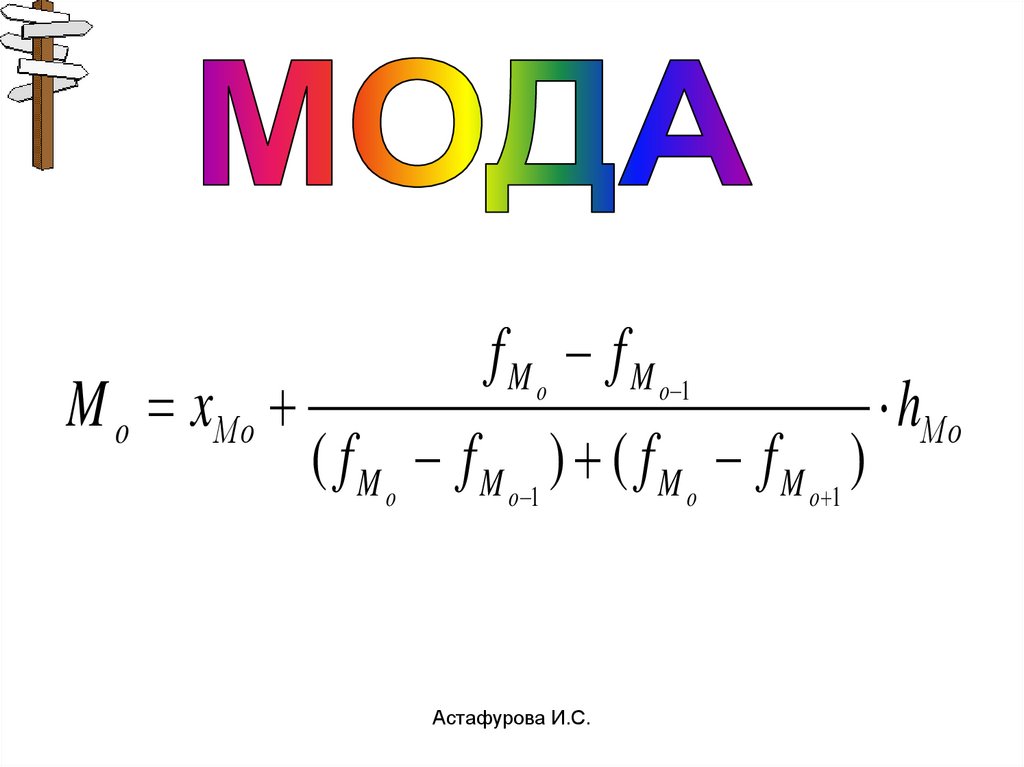
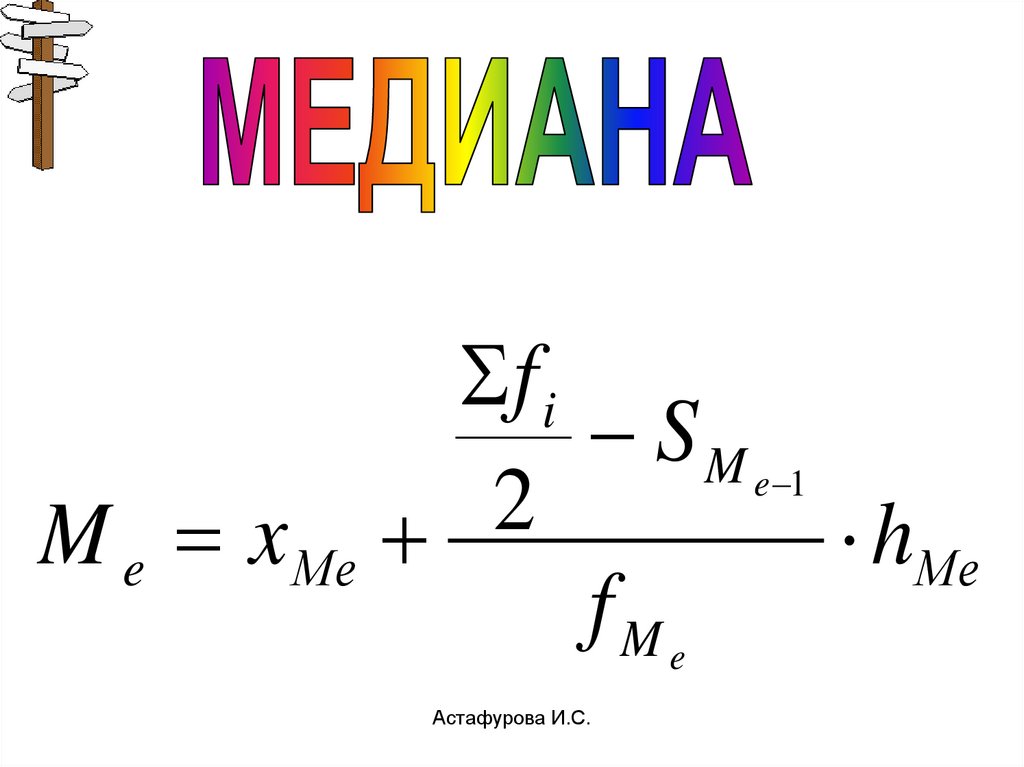



































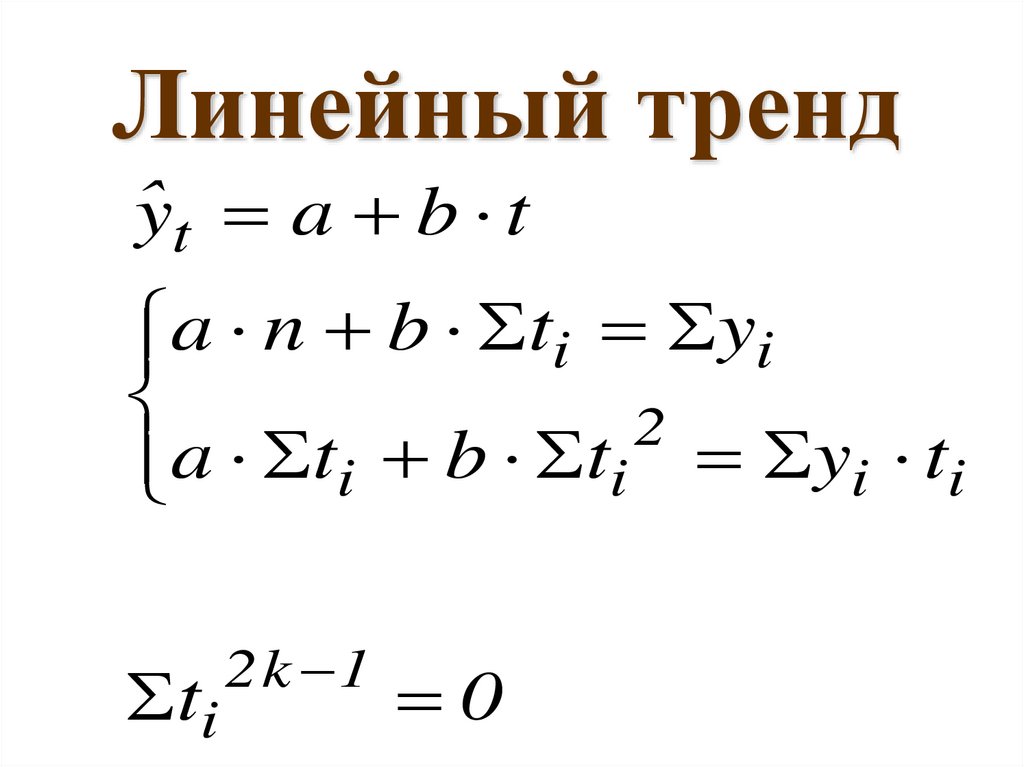
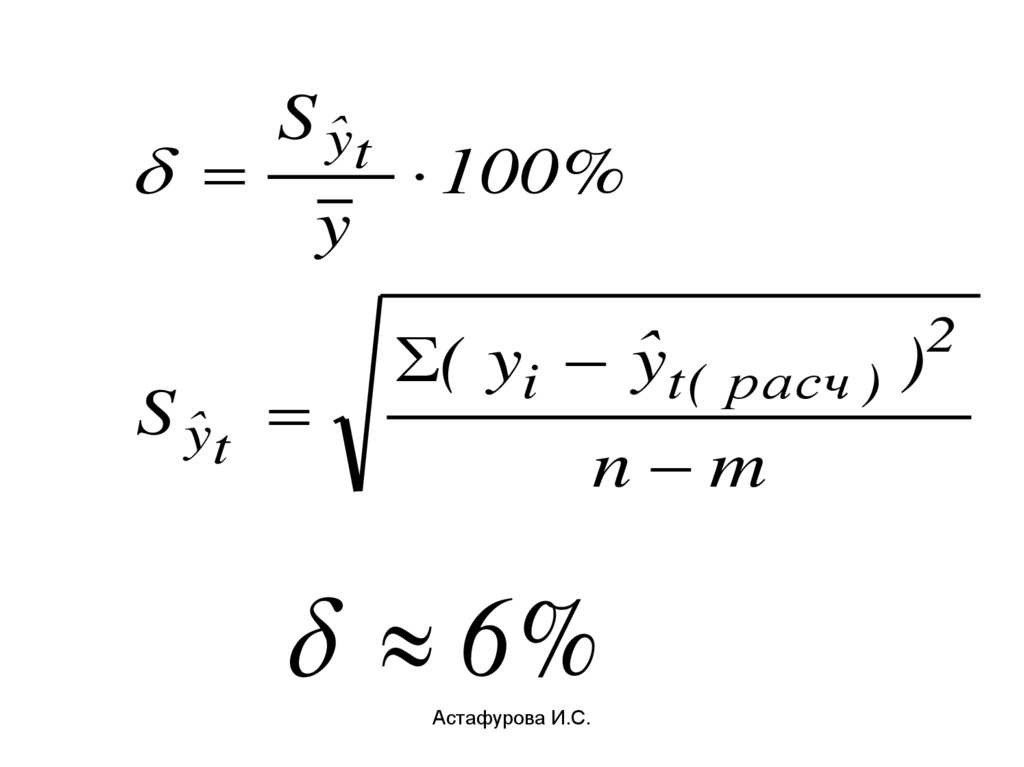

























 Математика
Математика








