Решение тригонометрических неравенств

1.

1
2
3
4
5
6
7
8
9
10
11
1
cos 2 x
2
2 sin 3x 1
1
sin x
2
0
sin 2 x 2
cos x 1
1
x
sin x 1
12
y
3
cos( x )
6
2
2
2

2.

Решить неравенство:
1
1
2
y
1
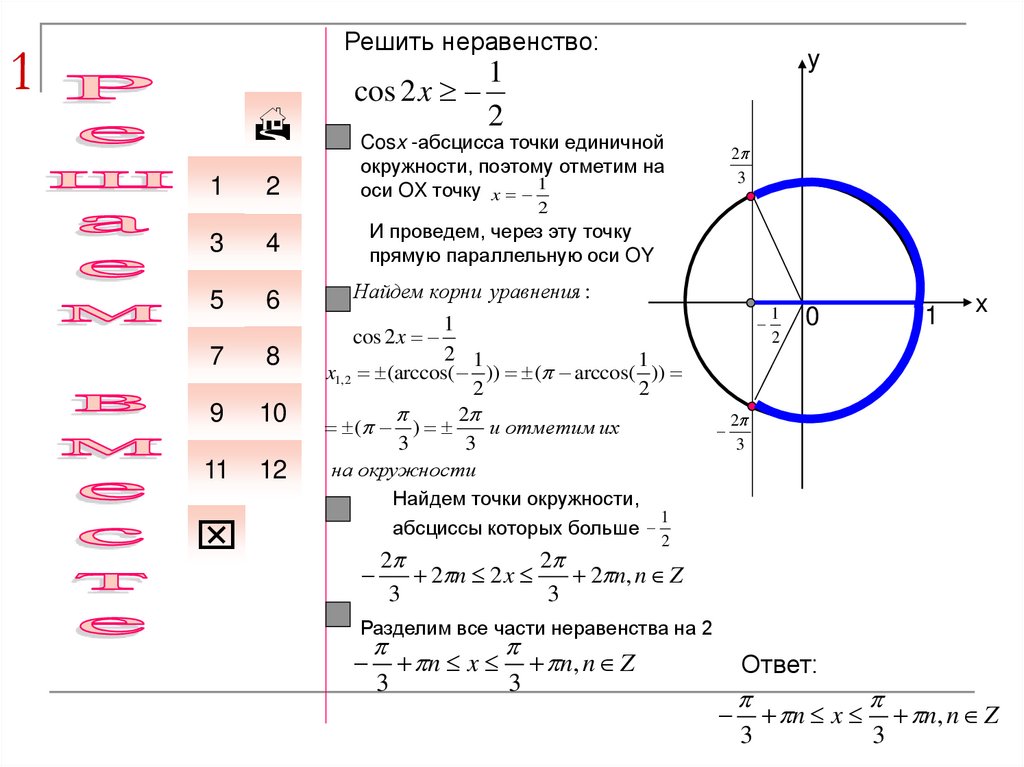
cos 2 x
2
Cosx -абсцисса точки единичной
окружности, поэтому отметим на
оси OX точку x 1
2
3
2
3
4
5
6
7
8
9
10
11
12
И проведем, через эту точку
прямую параллельную оси OY
Найдем корни уравнения :
1
2 1
1
x1, 2 (arccos( )) ( arccos( ))
2
2
2
( )
и отметим их
3
3
на окружности
1
2
cos 2 x
0
1
x
2
3
Найдем точки окружности,
1
абсциссы которых больше
2
2
2
2 n 2 x
2 n, n Z
3
3
Разделим все части неравенства на 2
3
n x
3
n, n Z
Ответ:
n x n, n Z
3
3

3.

Решить неравенство:
2
1
2
3
4
5
6
7
8
2
2
2
2
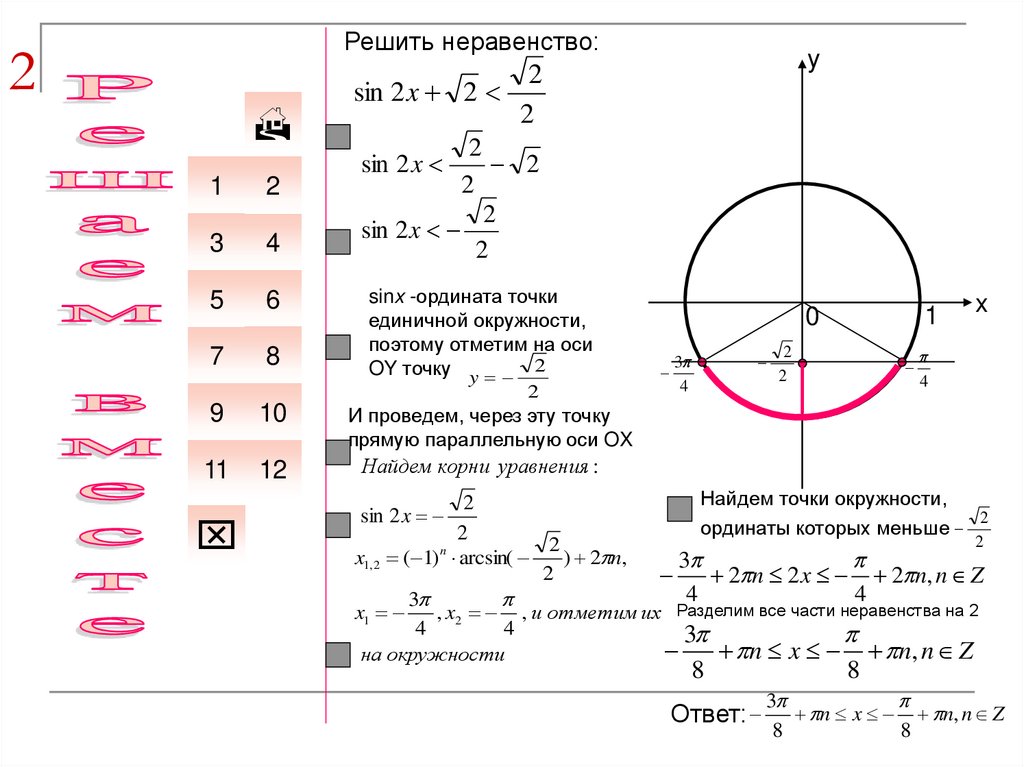
sin 2 x
2
sin 2 x
sinx -ордината точки
единичной окружности,
поэтому отметим на оси
OY точку y 2
2
9
10
11
12
y
2
sin 2 x 2
2
1
0
3
4
2
2
x
4
И проведем, через эту точку
прямую параллельную оси OX
Найдем корни уравнения :
Найдем точки окружности,
2
2
ординаты которых меньше
2
2
2
x1, 2 ( 1) n arcsin(
) 2 n,
3
2
2 n 2 x 2 n, n Z
4
4
3
x1
, x2 , и отметим их Разделим все части неравенства на 2
4
4
3
n
x
n, n Z
на окружности
sin 2 x
8
Ответ:
8
3
n x n, n Z
8
8

4.

3
Решить неравенство:
1
2
3
4
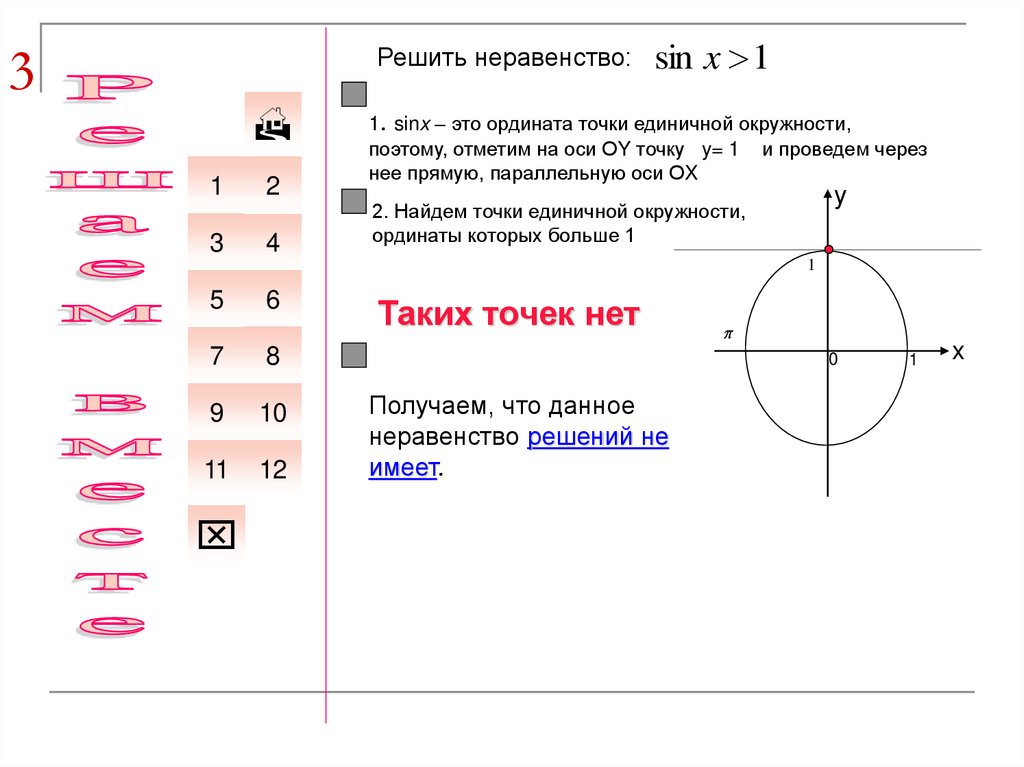
sin x 1
1. sinx – это ордината точки единичной окружности,
поэтому, отметим на оси ОY точку y= 1 и проведем через
нее прямую, параллельную оси ОX
y
2. Найдем точки единичной окружности,
ординаты которых больше 1
1
5
6
7
8
9
10
11
12
Таких точек нет
0
Получаем, что данное
неравенство решений не
имеет.
1
x

5.

Решить неравенство:
4
1
2
3
4
5
6
7
8
9
10
11
12
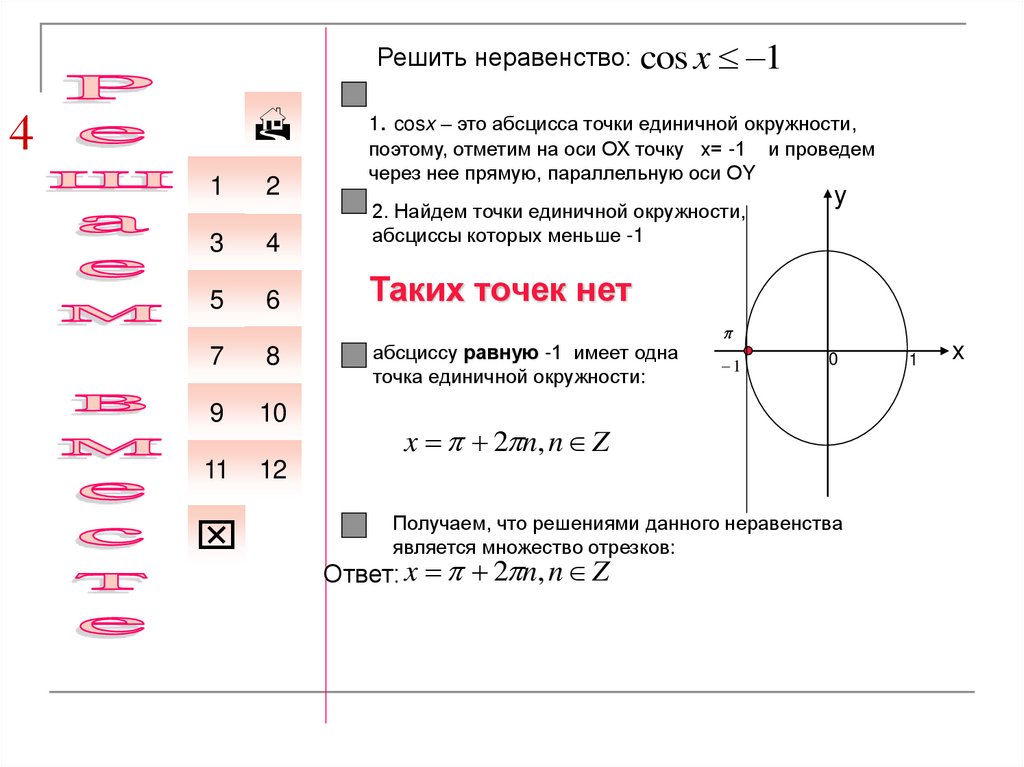
cos x 1
1. cosx – это абсцисса точки единичной окружности,
поэтому, отметим на оси ОХ точку х= -1 и проведем
через нее прямую, параллельную оси ОY
2. Найдем точки единичной окружности,
абсциссы которых меньше -1
y
Таких точек нет
абсциссу равную -1 имеет одна
точка единичной окружности:
1
0
x 2 n, n Z
Получаем, что решениями данного неравенства
является множество отрезков:
Ответ: x 2 n, n Z
1
x

6.

5
Решить неравенство:
1
2
3
4
5
6
7
8
9
10
11
12
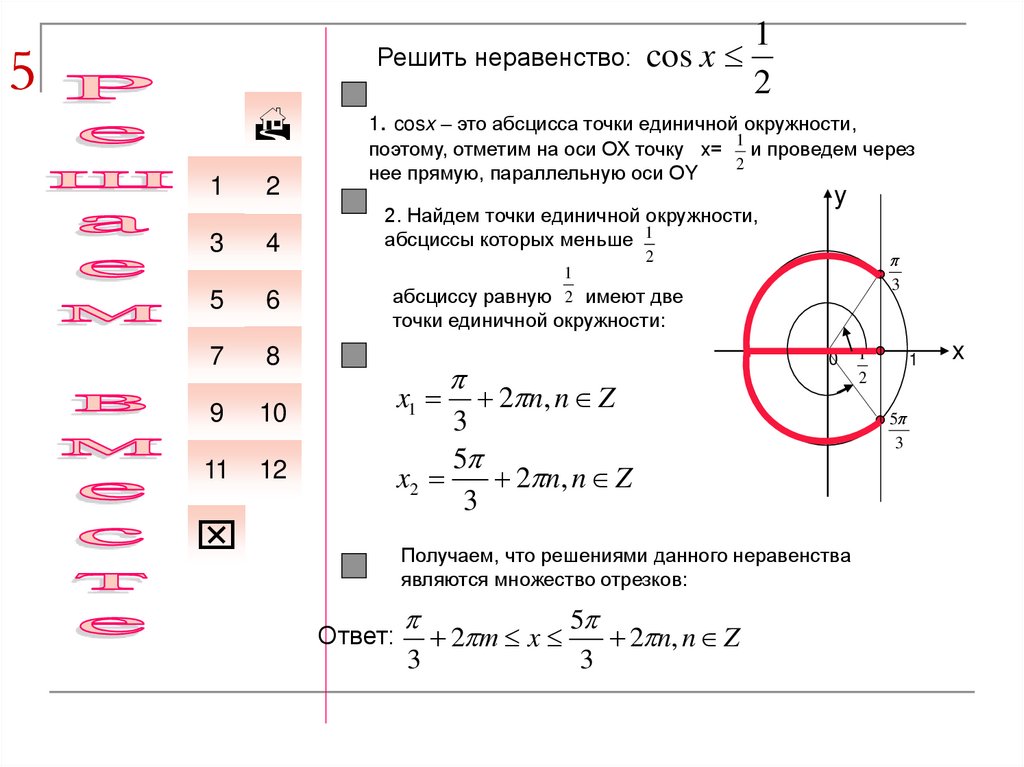
cos x
1
2
1. cosx – это абсцисса точки единичной окружности,
1
поэтому, отметим на оси ОХ точку х= и проведем через
2
нее прямую, параллельную оси ОY
2. Найдем точки единичной окружности,
абсциссы которых меньше 1
y
2
1
абсциссу равную 2 имеют две
3
точки единичной окружности:
x1
0
2 n, n Z
3
5
x2
2 n, n Z
3
Получаем, что решениями данного неравенства
являются множество отрезков:
Ответ:
3
2 т x
5
2 n, n Z
3
1
2
1
5
3
x

7.

6
Решить неравенство:
1
2
3
4
5
6
7
8
9
11
10
12
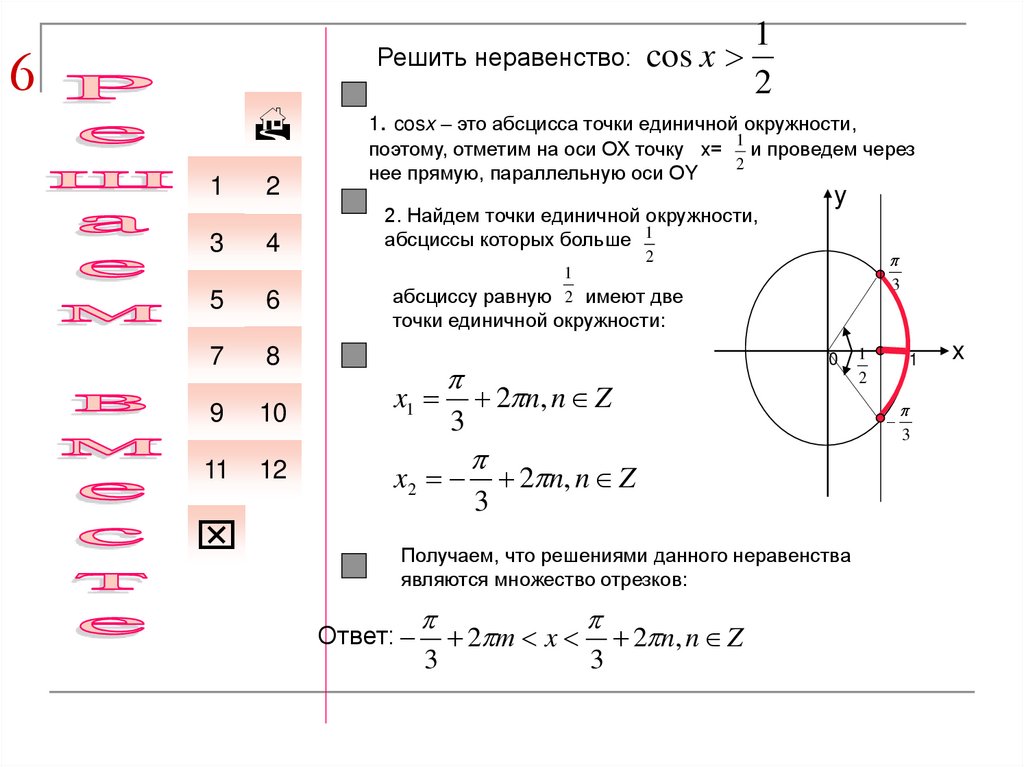
cos x
1
2
1. cosx – это абсцисса точки единичной окружности,
1
поэтому, отметим на оси ОХ точку х= и проведем через
2
нее прямую, параллельную оси ОY
2. Найдем точки единичной окружности,
абсциссы которых больше 1
y
2
1
абсциссу равную 2 имеют две
3
точки единичной окружности:
x1
3
x2
0
2 n, n Z
3
2 n, n Z
3
2 т x
3
1
Получаем, что решениями данного неравенства
являются множество отрезков:
Ответ:
1
2
2 n, n Z
3
x

8.

7
Решить неравенство:
1
2
3
4
5
6
7
8
9
10
11
12
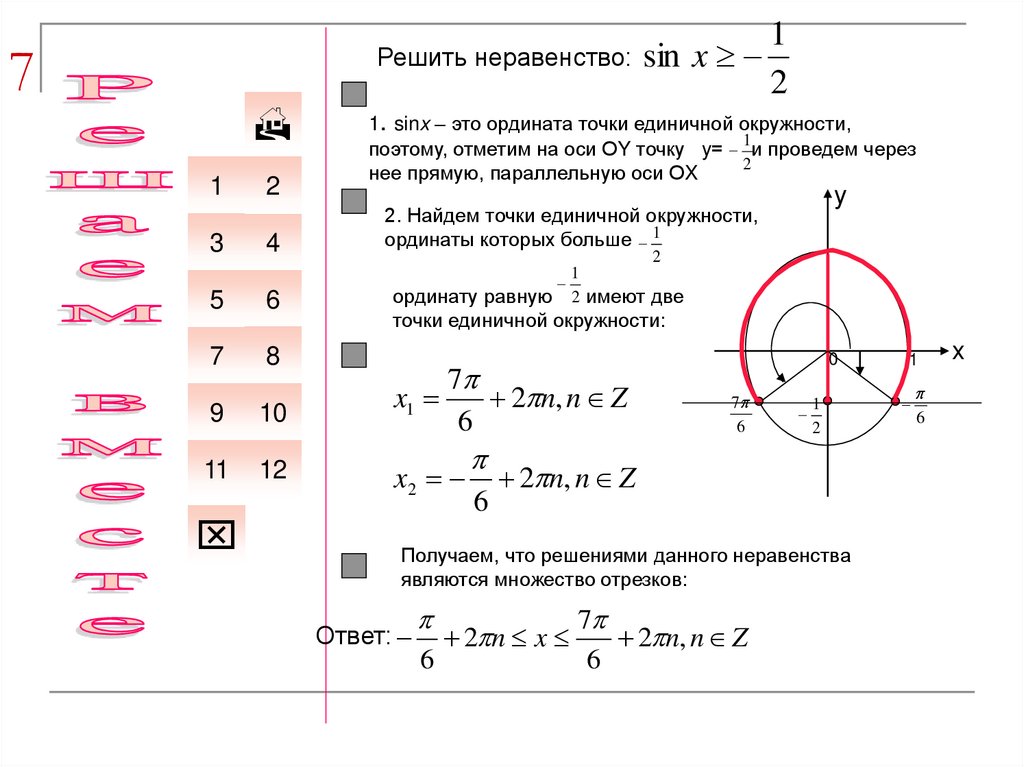
sin x
1
2
1. sinx – это ордината точки единичной окружности,
1
поэтому, отметим на оси ОY точку y= и проведем через
2
нее прямую, параллельную оси ОX
y
2. Найдем точки единичной окружности,
ординаты которых больше 1
2
1
ординату равную 2 имеют две
точки единичной окружности:
x1
7
2 n, n Z
6
x2
6
0
7
6
1
2
2 n, n Z
Получаем, что решениями данного неравенства
являются множество отрезков:
Ответ:
6
2 n x
7
2 n, n Z
6
1
6
x

9.

8
Решить неравенство:
1
2
3
4
5
6
7
8
9
10
11
12
sin x
1
2
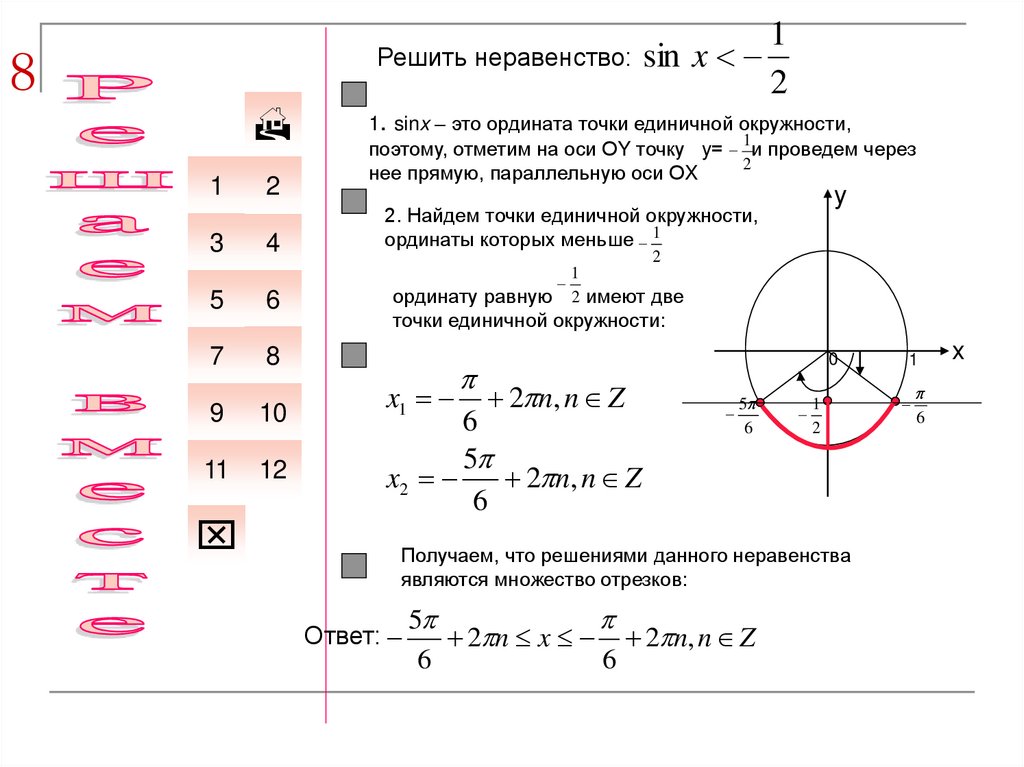
1. sinx – это ордината точки единичной окружности,
1
поэтому, отметим на оси ОY точку y= и проведем через
2
нее прямую, параллельную оси ОX
y
2. Найдем точки единичной окружности,
ординаты которых меньше 1
2
1
ординату равную 2 имеют две
точки единичной окружности:
x1
0
2 n, n Z
6
5
x2
2 n, n Z
6
5
6
1
2
Получаем, что решениями данного неравенства
являются множество отрезков:
Ответ:
5
2 n x 2 n, n Z
6
6
1
6
x

10.

Решить неравенство: 2 sin 3x 1
9
1. Выполним преобразования:
1
2
3
4
5
6
7
8
9
11
1
2
sin 3 x
(1)
2. sinx – это ордината точки единичной окружности,
1
поэтому, отметим на оси ОY точку y= и проведем через
2
y
нее прямую, параллельную оси ОX
3. Найдем точки единичной окружности,
ординаты которых больше 1
2
1
2 имеют две
ординату равную
точки единичной окружности:
x1
10
7
2 n, n Z
6
x2
12
6
0
7
6
1
2
1
x
6
2 n, n Z
Получаем, что решениями неравенства (1) являются
множество отрезков:
7
2 n 3 x
2 n, n Z
6
6
2 n
7 2 n
Ответ:
18
3
x
18
3
,n Z
Разделим все части
неравенства на 3, получим

11.

10
Решить неравенство:
1
2
3
4
5
6
точки единичной окружности:
7
8
x1
9
10
3
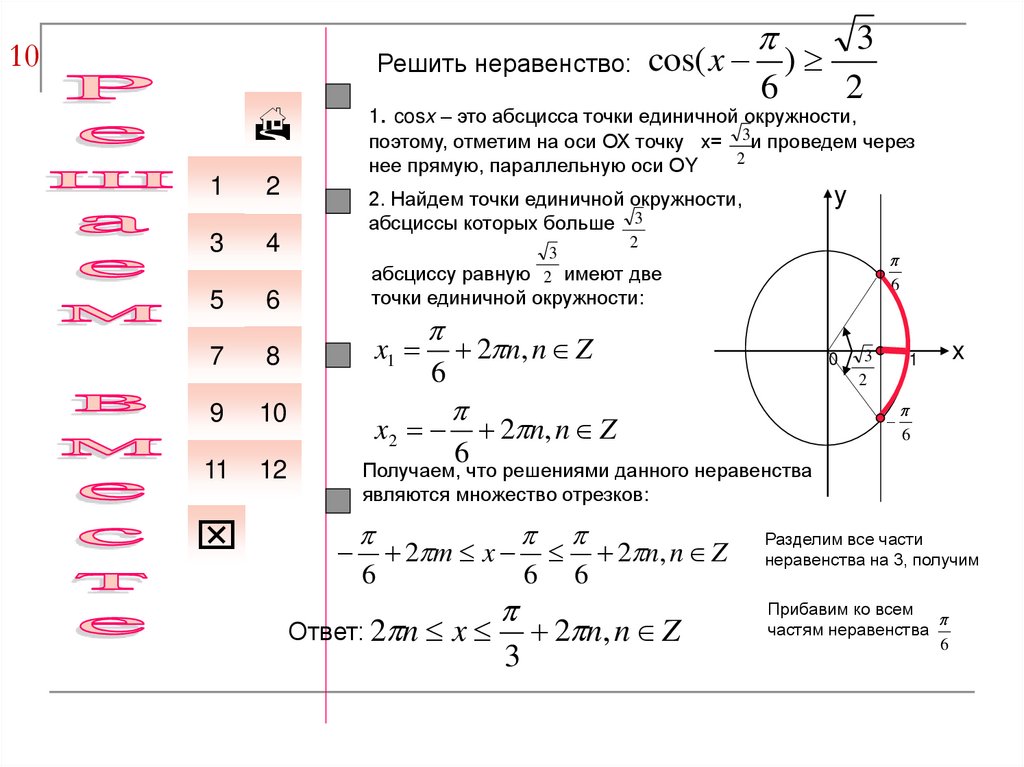
cos( x )
6
2
1. cosx – это абсцисса точки единичной окружности,
поэтому, отметим на оси ОХ точку х= 3и проведем через
2
нее прямую, параллельную оси ОY
11
y
2. Найдем точки единичной окружности,
абсциссы которых больше 3
2
3
абсциссу равную 2 имеют две
6
x2
6
2 n, n Z
6
0
2 n, n Z
3
2
1
x
6
Получаем, что решениями данного неравенства
являются множество отрезков:
12
6
2 т x
Ответ: 2 n
x
3
6
6
2 n, n Z
2 n, n Z
Разделим все части
неравенства на 3, получим
Прибавим ко всем
частям неравенства
6

12.

x
1
Решить неравенство: cos( 2)
3
2
11
1. cosx – это абсцисса точки единичной окружности,
1
поэтому, отметим на оси ОХ точку х= и проведем через
2
нее прямую, параллельную оси ОY
1
2
3
4
2
1
абсциссу равную 2 имеют две
5
6
точки единичной окружности:
7
9
11
y
2. Найдем точки единичной окружности,
абсциссы которых больше 1
x1
8
3
x2
10
3
2 n, n Z
3
0
2 n, n Z
1
2
1
x
3
Получаем, что решениями данного неравенства
являются множество отрезков:
12
3
x
2 2 n, n Z
3
3
x
2 2 n, n Z
3
3 3
Ответ: 6 6 n x 6 6 n, n Z
2 т
2 2 n
Прибавим ко всем
частям неравенства 2
Помножим все
части
неравенства на 3

13.

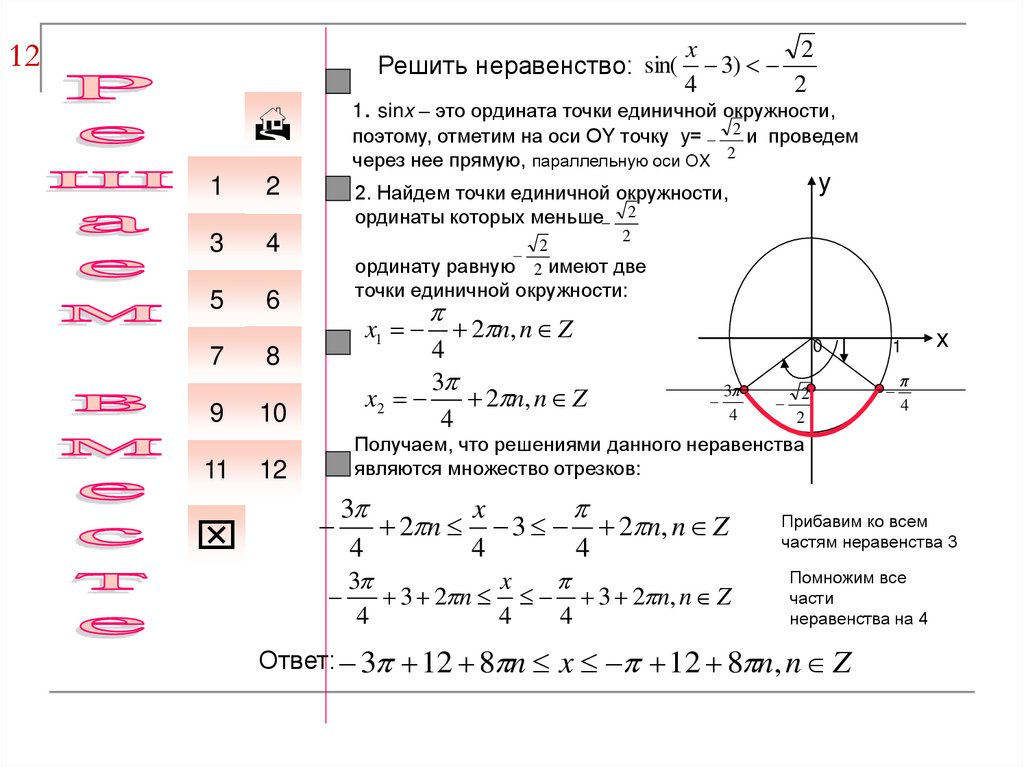
12
Решить неравенство: sin(
1
2
3
4
5
6
7
8
9
11
10
12
x
2
3)
4
2
1. sinx – это ордината точки единичной окружности,
поэтому, отметим на оси ОY точку y= 2 и проведем
через нее прямую, параллельную оси ОX 2
y
2. Найдем точки единичной окружности,
ординаты которых меньше 2
2
2
ординату равную 2 имеют две
точки единичной окружности:
2 n, n Z
4
3
x2
2 n, n Z
4
x1
0
3
4
2
2
1
x
4
Получаем, что решениями данного неравенства
являются множество отрезков:
3
x
2 n 3 2 n, n Z
4
4
4
3
x
3 2 n 3 2 n, n Z
4
4
4
Ответ: 3
Прибавим ко всем
частям неравенства 3
Помножим все
части
неравенства на 4
12 8 n x 12 8 n, n Z

14.

Учебник Колмогоров, стр. 77 - 79
Разобрать и записать в конспект
Пример 4 и Пример 6
ПР 17
Учебник Колмогоров, стр. 80
№ 157, № 159