Решение игр в смешанных стратегиях

1.

Тема 2. Решение игр в смешанных
стратегиях
Введение
Геометрическое решение игр 2 2, 2 n,
m 2
Приведение антагонистической игры к
паре взаимно двойственных задач
линейного программирования

2.

Введение
Сложная стратегия, состоящая в случайном
применении двух и более чистых стратегий с
смешанной
Наборы вероятностей (частот)
определенными частотами, называется
первого игрока
второго игрока
( p1 , p2 ,..., pm )
(q1 , q2 ,..., qn )
Основная теорема теории игр Дж. фон Неймана
Каждая конечная игра имеет по крайней мере
одно оптимальное решение в смешанных
стратегиях.

3.

1. Геометрическое решение игр 2 2, 2 n, m 2
1.1. Геометрическое решение игры 2 2
a11a12
A
a21a22
1.2. Геометрическое решение игры 2 n
a11a12...a1n
D
a21a22...a2 n
1.3. Геометрическое решение игры m 2
a11 a12
a21 a 22
Т
...........
a a
m1 m2

4.

1.1. Геометрическое решение игры 2 2
Графический метод решения игры
Этап 1. В декартовой системе координат pOH по оси абсцисс откладывается
отрезок, длина которого равна 1. Левый конец отрезка (точка р=0) соответствует
стратегии A1 , правый – стратегии A (р=1).
2
Промежуточные точки оси абсцисс соответствуют вероятностям некоторых
смешанных стратегий ( p1 , p2 )
Этап 2. На левой оси – оси ординат, откладываются выигрыши стратегии
Этап 3. На линии, параллельной оси ординат, из точки 1 откладываются
выигрыши стратегии A
2
Этап 4. Соединяем точки
прямой
'
B2 B2
a11,a21
прямой
'
B1 B1
, точки
a12 ,a22
A1

5.

Интерпретация результатов

6.

Для уточнения и проверки результатов графического
решения можно дополнительно решить системы
a11 a12
A
a21 a22
q1 q 2
для первого игрока
a11 p1 a21 p2
a12 p1 a22 p2
p p 1
2
1
P1
P2
для второго игрока
p1
a22 a21
a11 a22 a21 a12
p2
a11 a12
a11 a22 a21 a12
q1
a22 a12
a11 a22 a12 a21
q2
a11 a21
a11 a22 a12 a21
a11a22 a12a21
a11 a22 a12 a21
a11q1 a12q2
a21q1 a22q2
q q 1
2
1

7.

Пример
Игроки
В1
В2
A1
0,3
0,8
A2
0,7
0,4
Решение
В1
В2
A1
0,3
0,8
Минимумы
строк
0,3
A2
0,7
0,4
0,4
0,7
0,8
Игроки
Максимумы
столбцов

8.

Выводы

9.

1.2. Геометрическое решение игры 2 n
a11a12...a1n
D
a21a22...a2 n
Игроки
В1
q1
p1
A1
A2
a11
p2 1 p1
a21
….
Вn
В2
….
qn
q2
….
a12
a1n
….
a22
a2 n
Найти смешанные стратегии игроков
A
1
2
S (p , p )
B
1
2
n
S (q , q ,..., q )

10.

Пример
10 8 6 4 2 3
D
1 2 4 3 12 6
1. Исключим из платежной матрицы заведомо невыгодные стратегии:
Игроки
В1
В2
В3
В4
В5
В6
A1
A2
10
1
8
2
6
4
4
3
2
12
3
6
Игроки
В1
В2
В4
В5
В6
A1
10
8
4
2
3
A2
1
2
3
12
6

11.

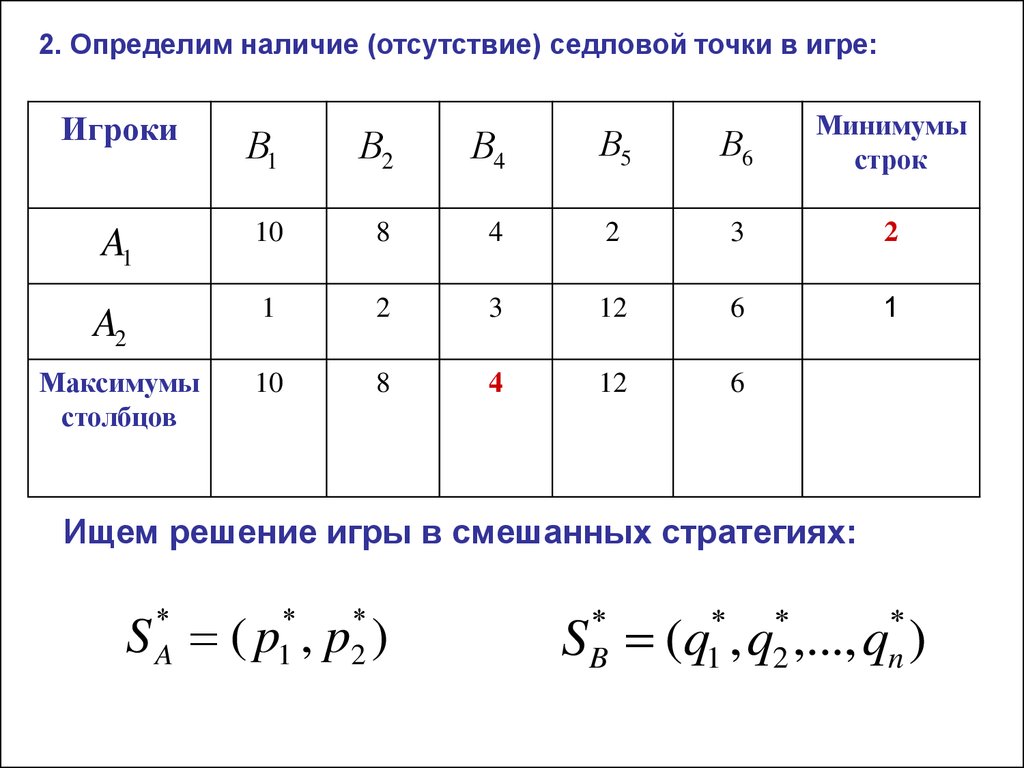
2. Определим наличие (отсутствие) седловой точки в игре:
Игроки
В1
В2
В4
В5
В6
Минимумы
строк
A1
10
8
4
2
3
2
A2
1
2
3
12
6
1
10
8
4
12
6
Максимумы
столбцов
Ищем решение игры в смешанных стратегиях:
A
1
2
S (p , p )
B
1
2
n
S (q , q ,..., q )

12.

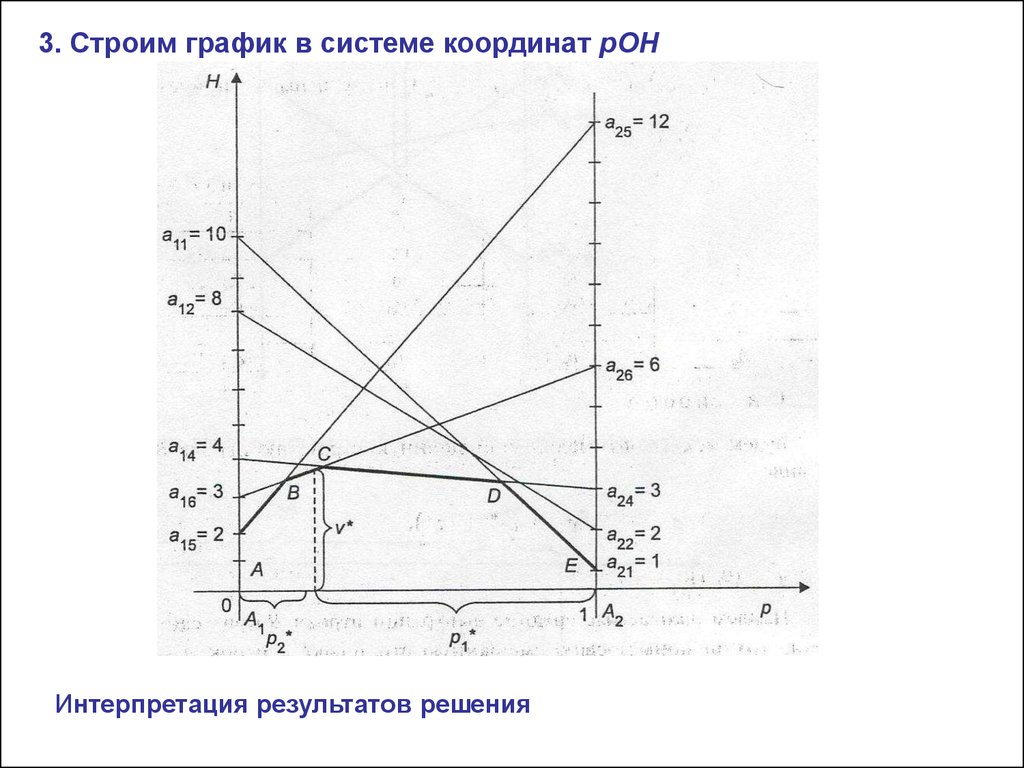
3. Строим график в системе координат pOH
Интерпретация результатов решения

13.

1
2
4
p , p ,q ,q
4. Определим значения вероятностей
и цены игры
Активные
стратегии А
Игроки
В4
В6
A1
4
3
p1
A2
3
6
p2
Активные
стратегии В
4
6
q
q
игрок А:
4 p1 3 p2
3 p1 6 p2
p1 p2 1
Выводы
6
игрок В:
3 1 15
3 1
S A ; , S B 0;0;0; ;0; ,
4 4
4
4 4
4q4 3q6
3q4 6q6
q4 q6 1

14.

1.3. Геометрическое
решение игры m 2
a11 a12
a21 a 22
Т
...........
a a
m1 m2
Необходимо найти смешанные стратегии игроков:
A
1
2
S ( p , p ,..., pm )
B
1
2
S (q , q )

15.

В2
A1
p1
В1
q1
a11
A2
p2
a21
a22
…
…
…
…
pm
am1
Игроки
Am
q2
a12
am 2
Решение проводят с позиций игрока B,
у которого две стратегии

16.

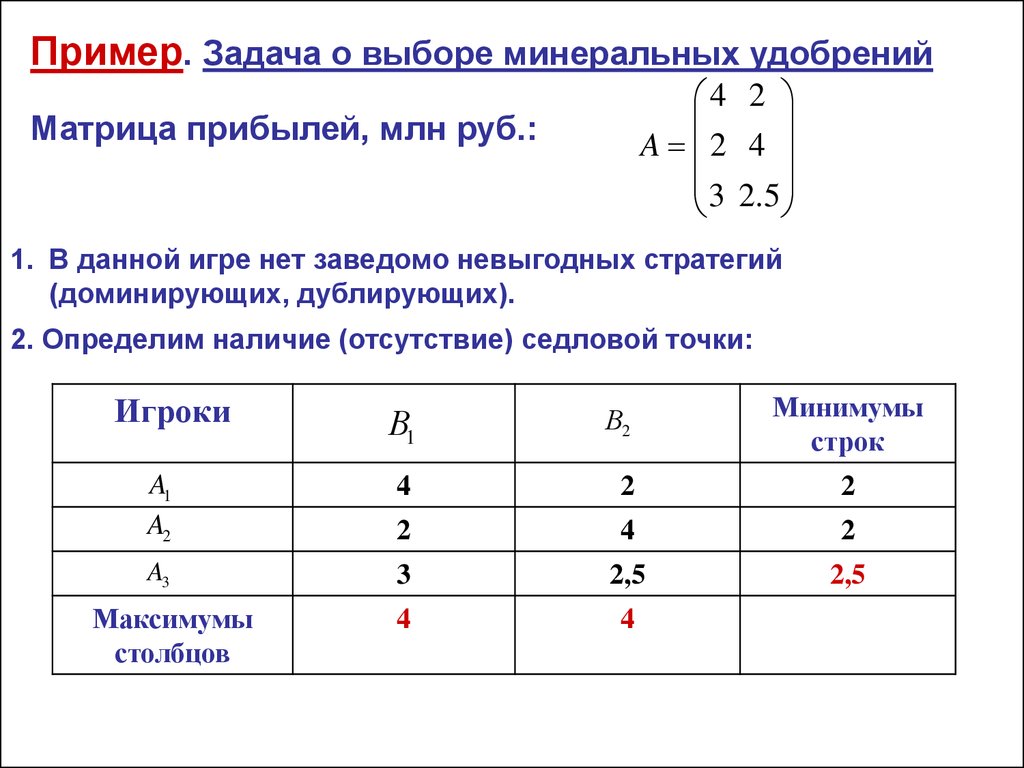
Пример. Задача о выборе минеральных удобрений
4 2
A 2 4
3 2.5
Матрица прибылей, млн руб.:
1. В данной игре нет заведомо невыгодных стратегий
(доминирующих, дублирующих).
2. Определим наличие (отсутствие) седловой точки:
Игроки
Минимумы
строк
В1
В2
A1
A2
4
2
2
2
4
2
A3
3
2,5
2,5
4
4
Максимумы
столбцов

17.

3. Строим график в системе координат qOH

18.

4. Определим значения вероятностей p1 , p 2 , q1 , q 2
и цены игры
Игроки
A1
A2
Активные
стратегии В
Активные
стратегии А
В2
В1
4
2
p1
2
4
p2
1
q
q
2
игрок В:
игрок А:
4 p 2 p
2 p1 4 p2
p1 p2 1
1
2
1 1
1 1
S A ; ;0 , S B ; , 3
2 2
2 2
Выводы
4q1 2q2
2q1 4q2
q1 q2 1

19.

Общая схема решения игр 2 n и m 2
1. Строят прямые, соответствующие стратегиям игрока В или
А.
2. Находят две стратегии игрока В или А, которым
соответствуют две прямые, пересекающиеся в точке с
максимальной (минимальной) ординатой. Эти стратегии
являются активными в оптимальной смешанной стратегии
игрока В или А.
3. Находят координаты точки пересечения, тем самым
определяя оптимальную стратегию игрока А или В и цену
игры.
4. Оптимальную стратегию другого игрока находят, решая
систему уравнений, включающую его активные стратегии.

20.

2. Приведение антагонистической игры к паре
взаимно двойственных задач линейного программирования
m n
Игра порядка
Игрок А
Игрок В
B1
B2
…
Bk
…
Bn
A1
a11
a12
…
a1k
…
a1n
A2
a 21
a 22
…
a 2k
…
a 2n
…
…
…
…
a in
…
…
…
…
Ai
a i1
a i2
…
…
…
…
…
…
…
…
a m1
a m2
…
a mk
…
a mn
Am
A
1
2
S ( p , p ,..., pm )
a1ik
B
1
2
n
S (q , q ,..., q )

21.

Задача игрока А
Задача игрока В
F ( X ) x1 x2 ... xm min
Z (Y ) y1 y2 ... yn max
a11x1 a21x2 ... am1 xm 1
a x a x ... a x 1
22 2
m2 m
12 1
..........................................
a x a x ... a x 1
2n 2
mn m
1n 1
xi 0, i 1,..., m
a11 y1 a12 y2 ... an1 yn 1
a21 y1 a22 y2 ... an 2 yn 1
..........................................
a y a y ... a y 1
mn n
m1 1 m 2 2
y j 0, j 1,..., n
X x1 , x2 ,..., xm
1
2
Y y , y ,..., y
n
1
1
Fmin Z max
pi xi
q j y j

22.

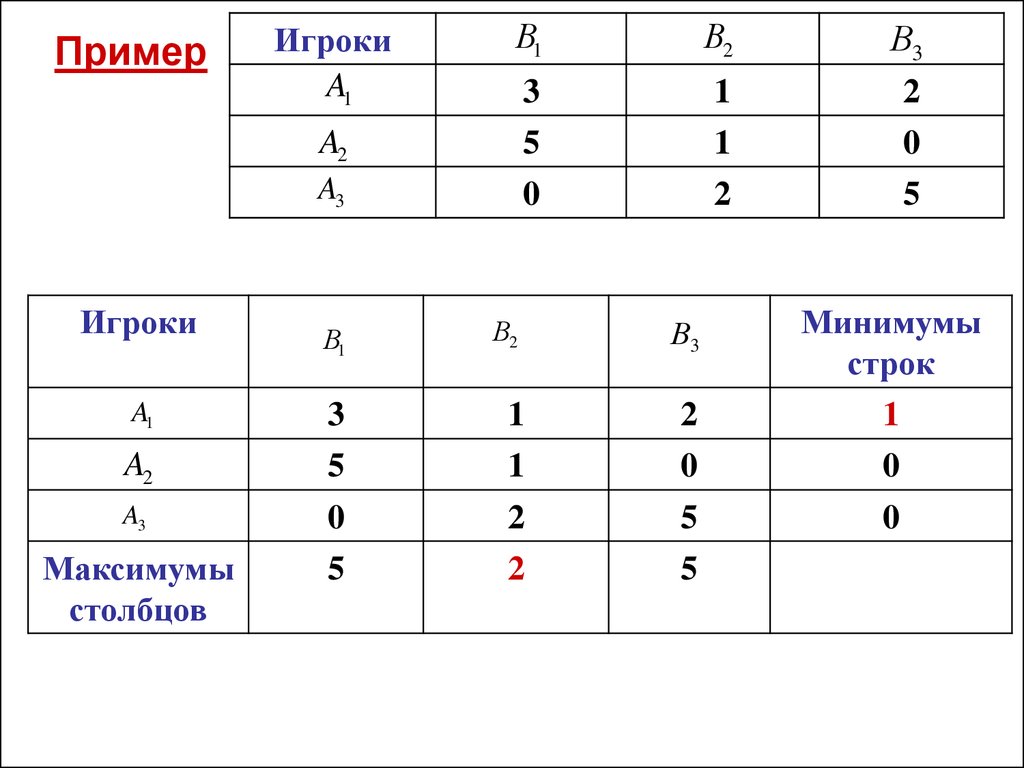
Пример
Игроки
A1
A2
A3
Максимумы
столбцов
В1
В2
В3
A2
3
5
1
1
2
0
A3
0
2
5
Игроки
A1
В1
В2
В3
3
5
1
1
2
0
0
5
2
2
5
5
Минимумы
строк
1
0
0

23.

Задача игрока А
Задача игрока В
F ( X ) x1 x2 x3 min
Z (Y ) y1 y2 y3 max
3 x1 5 x2 1
1x 1x 2 x 1
1
2
3
2 x1 5 x3 1
xi 0, i 1,2,3
3 y1 1 y2 2 y3 1
5 y 1 y 1
1
2
2 y 2 5 y3 1
y j 0, j 1,2,3
1
1
1
5
1
2
Fmin Z max 0
3
5 5
1 2
X 0, ,
5 5
1 1
Y , ,0
10 2
i
i
p x
1 2
S 0, ,
3 3
A
q j y j
1 5
S , ,0
6 6
B

24.

При решении произвольной конечной игры разме
m n
рекомендуется придерживаться следующей схем
1. Исключить из платежной матрицы заведомо невыгодные стратегии.
2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли
игра седловую точку. Если седловая точка есть, то соответствующие ей
стратегии игроков будут оптимальными, а цена игры совпадает с верхней
(нижней) ценой.
3. Если седловая точка отсутствует, то решение следует искать в
смешанных стратегиях. Игры размера m n решаются путем сведения к
паре взаимно двойственных задач линейного программирования. Для игр
размера 2 n , m 2 возможно применить графо-аналитический метод
решения.