Интегральное исчисление

1.

ТЕМА ЛЕКЦИИ:
«ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ»
1.Непределенный интеграл
2. Определенный интеграл

2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Обозначение
неопределённого
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
интеграла
f x dx F x c
где f(x) – подинтегральная функция,
f(x)dx
–
подинтегральное
(дифференциал),
с – постоянная интегрирования.
выражение

3. Неопределенный интеграл

4. Таблица неопределенных интегралов

1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x

5. Определенный интеграл

6. Определенный интеграл

Определение.
n
Выражение f xi xi , где
i 1
xi xi xi 1 , называется
интегральной суммой функции f x
на отрезке a, b .

7. Определенный интеграл

.
Определенный интеграл
Определение.
Если существует конечный
n
lim
f xi xi , не
max xi 0 i 1
зависящий ни от способа разбиения отрезка
a, b на части, ни от выбора точек xi xi 1 , xi ,
то этот предел называется определенным
интегралом функции f x на отрезке a, b

8. Обозначение определённого интеграла

b
f x dx
a
где а, в – пределы интегрирования

9.

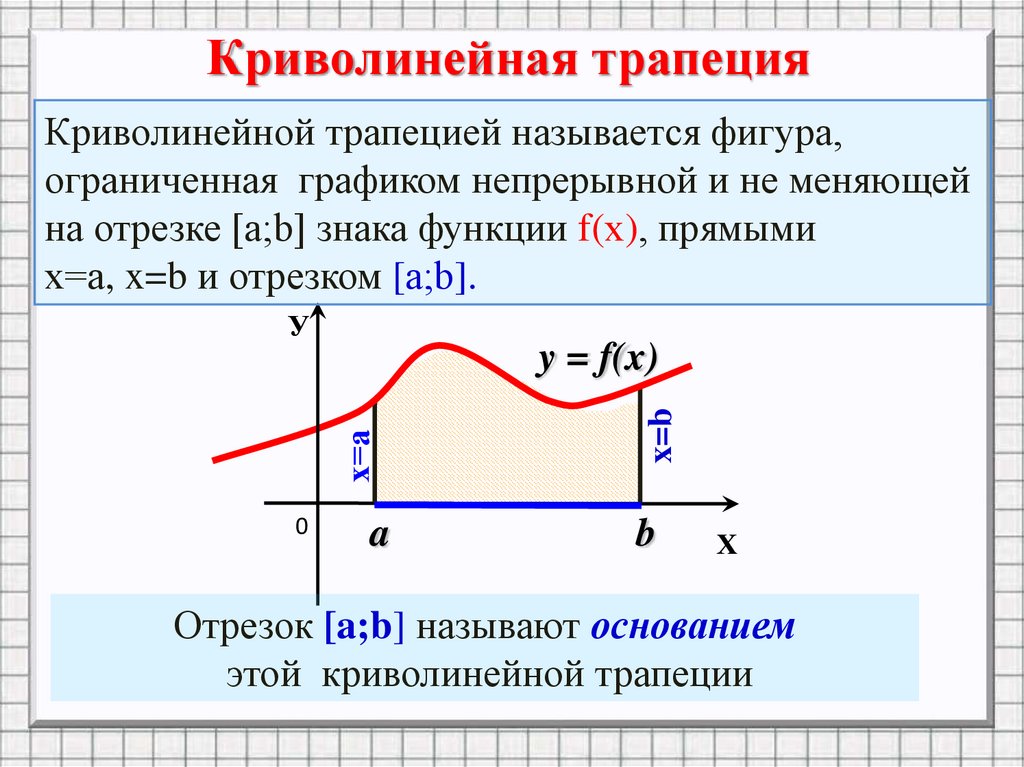
Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции

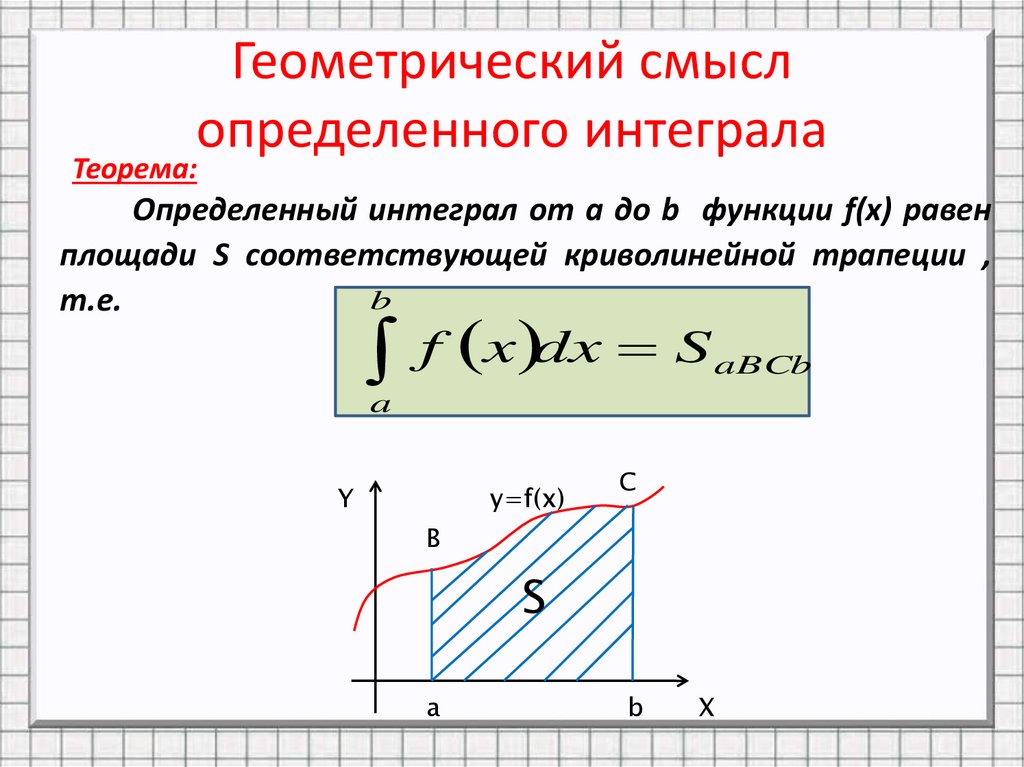
10. Геометрический смысл определенного интеграла

Теорема:
Определенный интеграл от a до b функции f(x) равен
площади S соответствующей криволинейной трапеции ,
b
т.е.
f x dx S
aBCb
a
Y
y=f(x)
C
B
S
а
b
X

11. Свойства определенного интеграла

a
1. f x dx 0 ;
a
b
2. dx b a ;
a
b
a
3. f x dx f x dx ;
a
b
b
4. f1 x f 2 x dx f1 x dx f 2 x dx ;
a
b
b
a
a

12. Свойства определенного интеграла

b
b
a
b
a
5. Kf x dx K f x dx ;
c
b
a
c
6. f x dx f x dx f x dx ;
a
b
7. f x dx 0 , если f x 0 .
a

13.

Формула вычисления площади с
помощью интеграла
Пусть функция f(x) непрерывна
на отрезке [а;b] и пусть F(х) есть
какая – либо её первообразная.
Тогда справедливо равенство
формула Ньютона-Лейбница

14.

ПРАКТИКА:
«ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ»

15. Пример

2 1
2
6х
6х 2
2
3 2
6
х
dx
2
х
3
3
3
3
2 1
3
3
2
( 2 2 ) ( 2 ( 3) ) 16 ( 54)
3
16 54 70
3

16. Пример

2 1
4
1 1
3х
х
3х
х
х
3
0 (3x x)dx ( 2 1 1 1) ( 3 2 ) ( х 2 )
3
2
2
2
2
4
0
3
(4 ) (0 ) (64 8) (0 0) 72
2
2
3
2

17. Пример

2 1
1 1
0 1
6
х
4
х
3
х
2
3
2
(
6
x
4
x
3
)
dx
(
)
(
2
х
2
х
3х)
1
2 1 1 1 0 1
2
(2 2 3 2 2 2 3 2) (2 13 2 12 3 1)
(16 8 6) (2 2 3) 14 3 11

18. Задание 1:Вычислить интеграл

2
1) 4хdx
0
2) 6 х dx
2
3
2
3) (7 x 1)dx
1
2
4) ( x 2 3)dx
1
5) (3x 2 x)dx
0
6) 6хdx
0
2
4
3
3
7) 3 х 2 dx
2
2
8) (5 x 1)dx
1
1
9) ( x 2 3)dx
2
3
10) (3x 2 2 x)dx
0

19. Задание 1: Вычислить интеграл

0
1) ( x 4 x 6)dx
2
3
1
0
7) ( x 2 6 x 3)dx
3
1
2) (2 x 3x 2)dx
8) (5 x 2 3x 13)dx
3) (8 x 25)dx
9) (6 x 17)dx
2
4
1
1
3
4) (6 x 2 x 5)dx
2
2
1
5) (15 x 4 6)dx
2
3
6) 2dx
7
4
1
1
3
10) (3x 2 4 x 7)dx
2
1
11) (18 x 5 2)dx
2
4
12) 5dx
8