Похожие презентации:
Численное решение алгебраических и трансцендентных уравнений
1. Тема 3
Численное решениеалгебраических и трансцендентных
уравнений.
2.
3.
4.
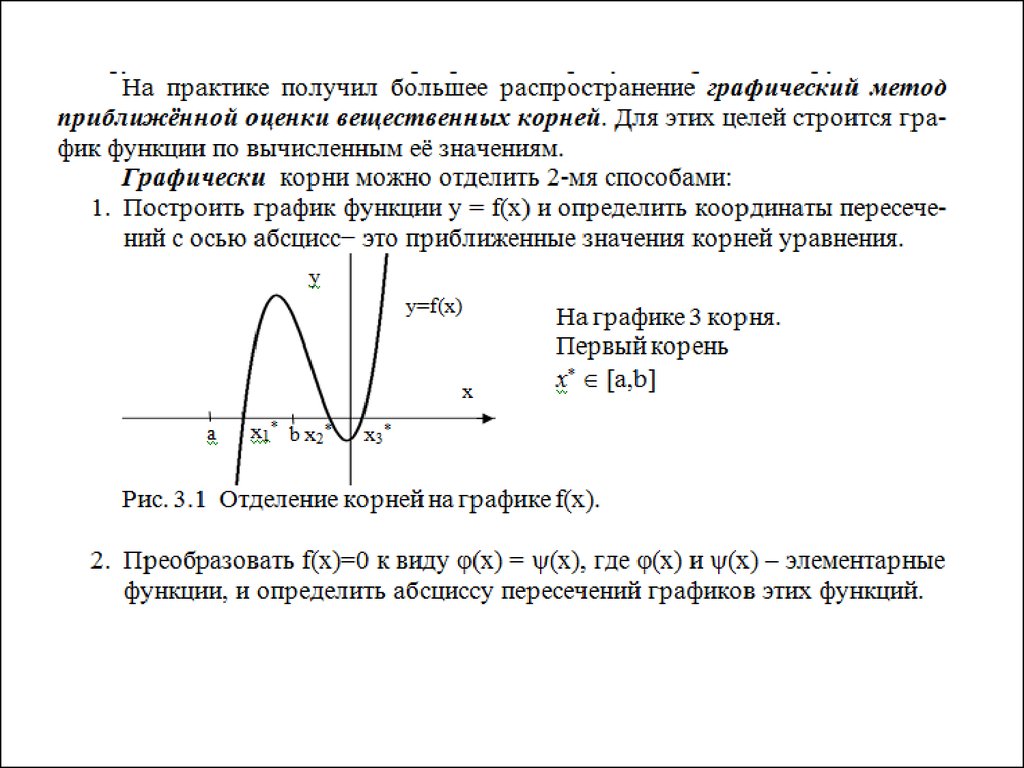
5. 3.1. Отделение корней нелинейного уравнения.
6.
7.
8.
9.
10.
11.
12.
13.
Рис. 3.3 Схема алгоритма отделениякорней.
14.
Root_Separation2
Исходные данные:
Ввод
3
a – начало отрезка поиска корней
a, b, Δx
b – конец отрезка поиска корней
ya − значение функции в начале поиска
корня
Δx –очередного
шаг изменения
неизвестного
x=a
нет
ya= f(a)
x≤b
k=0
4
k − номер корня
да
5
6
x = x + Δx
7
y = f(x)
y* ya ≤ 0
нет
да
8
ya = y
9
k=k+1
Вывод
k, x – Δx, x, y
Результаты:
k− номер корня
x - Δx – начало отрезка существования корня;
x – конец отрезка существования
10
Конец
Корня; y – значение функции при x.
15. 3.2. Алгоритмы уточнения корней уравнения.
16.
17.
18.
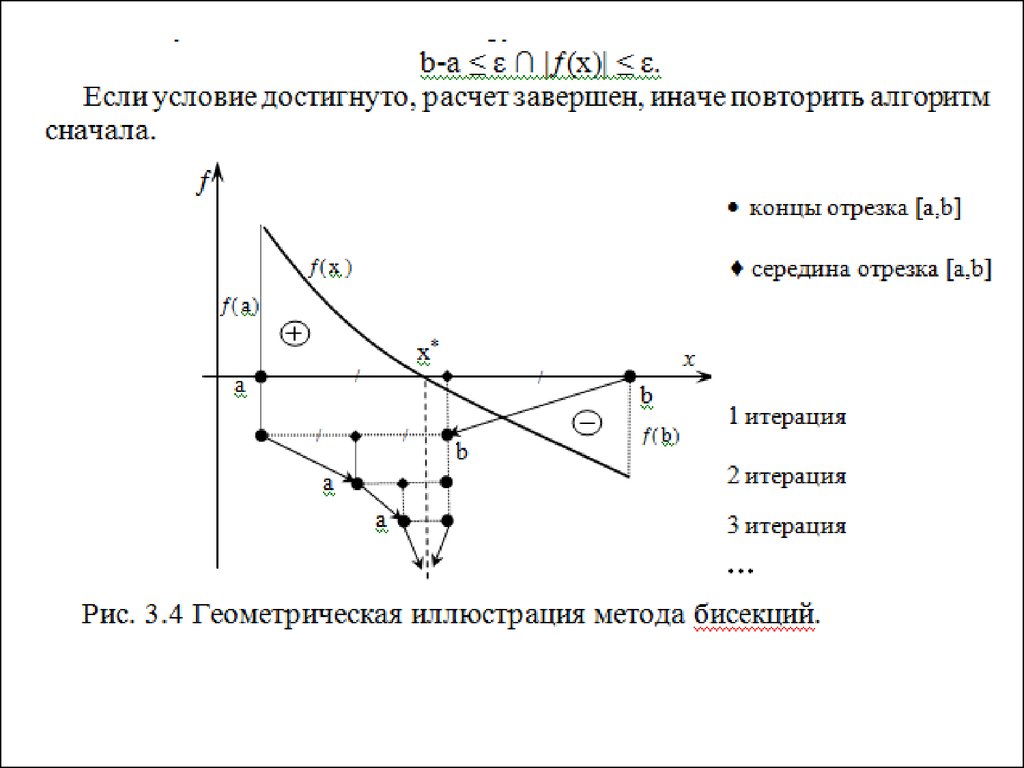
Рис. 3.5 Схема алгоритмаметода бисекций (дихотомии)
19.
1Входные данные:
–b=x
заданная точность;
a – левая граница отрезка;
b – правая граница отрезка.
Bisection
2
ya =f(a)
yb =f(b)
3
ya yb 0
д
i=0 а
4
5
11
Вывод
"Корней нет"
i = i+1;
x =(a+b)/2
6
12
Stop
y=f(x)
7 ya y>0
8
нет 9
нет
a=x
д
а
|y| /\ b-a<ε
10
д
а
Exit
нет
7
Выходные данные:
x – приближенное значение
корня;
y – значение функции при
найденном корне х;
i – выполненное число итераций.
20.
21.
22.
23.
24.
25.
26.
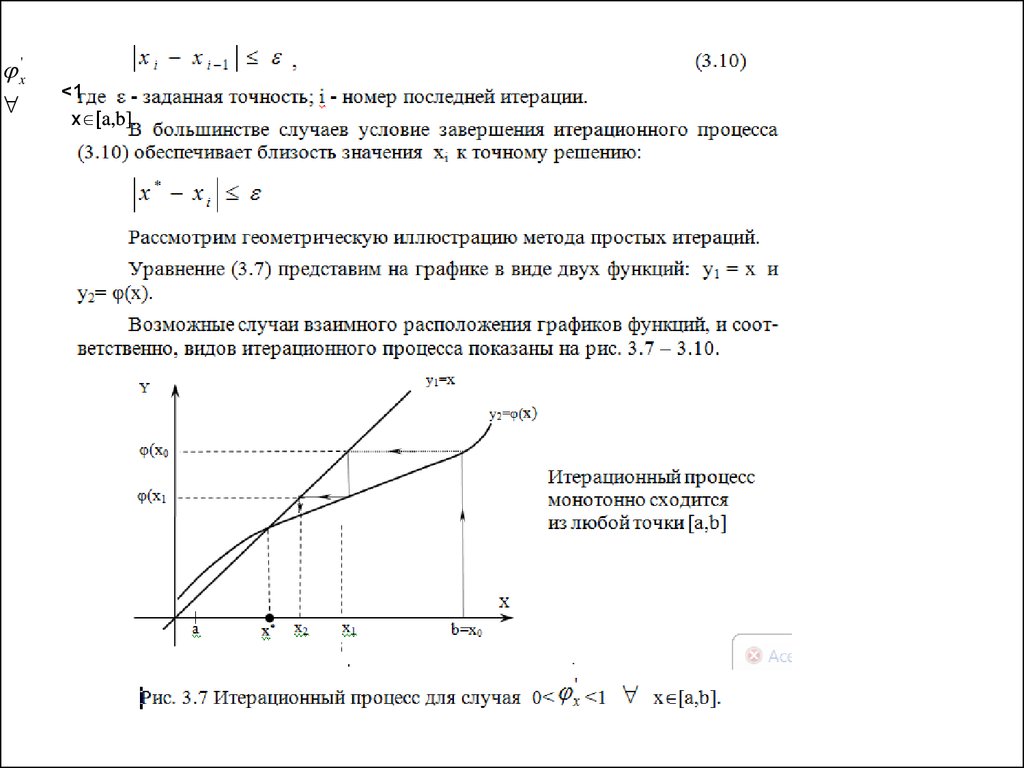
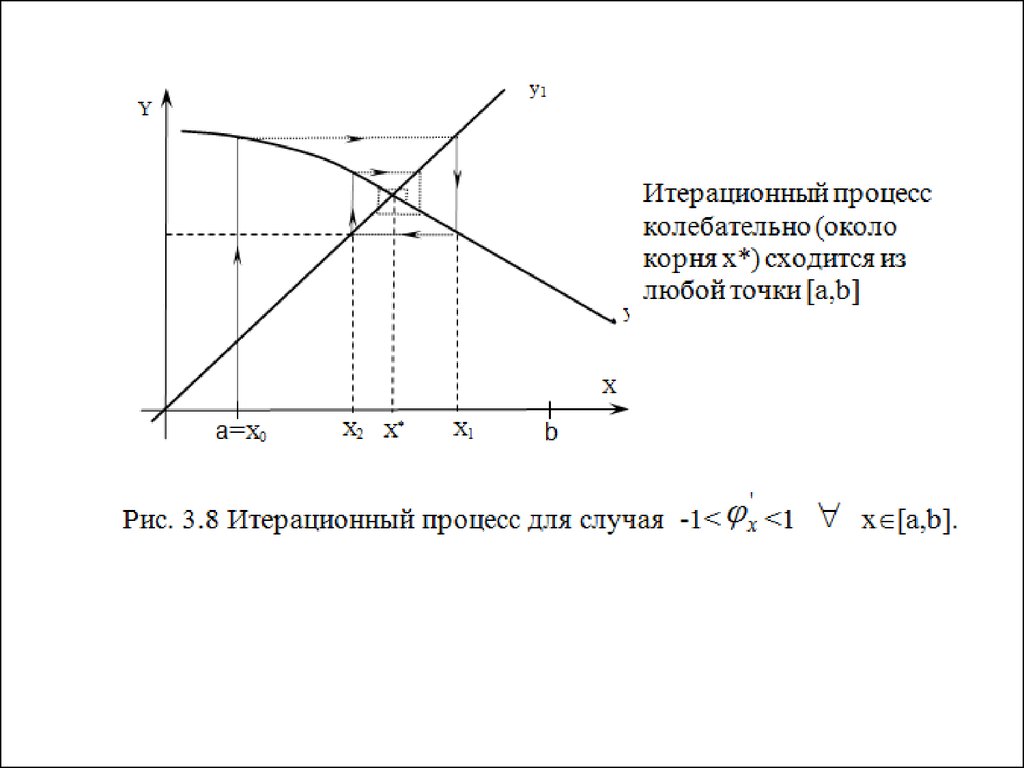
x'<1
x [a,b].
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
Проверим полученное значение, подставив в исходное уравнение:f ( x 6 ) 0,453917 3 2 0,453917 1 0,093525 0,907834 1 0,001359
Значение f(x) близко к 0 с точностью, близкой к ε,
следовательно, корень уточнен правильно.
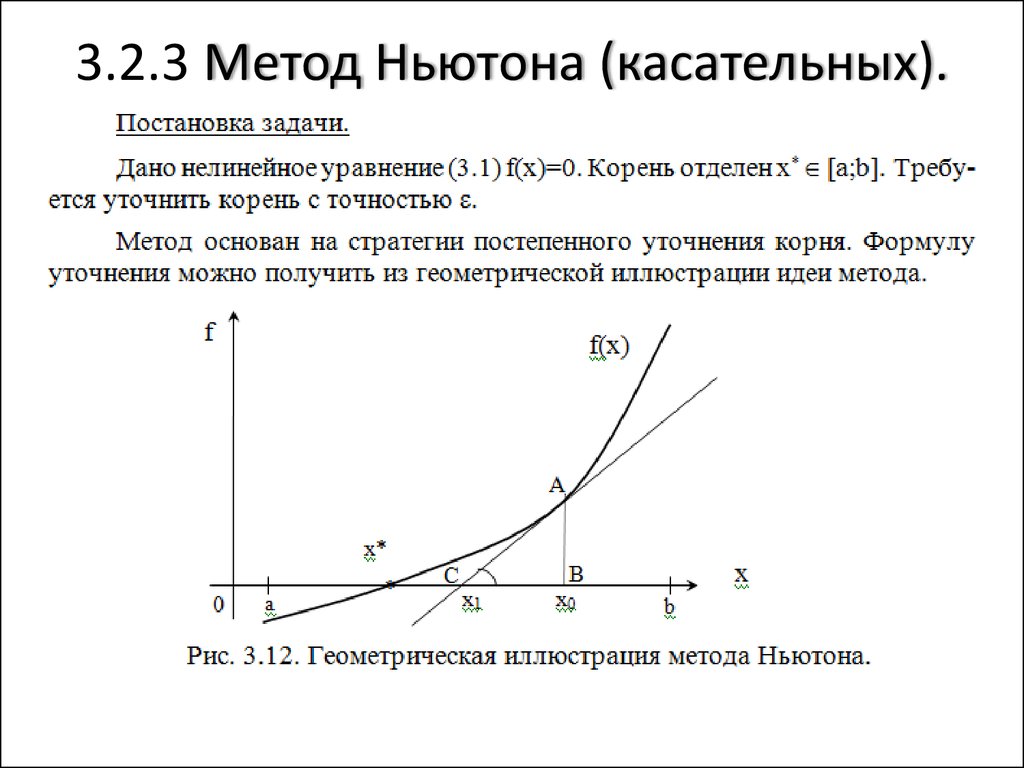
37. 3.2.3 Метод Ньютона (касательных).
38.
39.
40.
41.
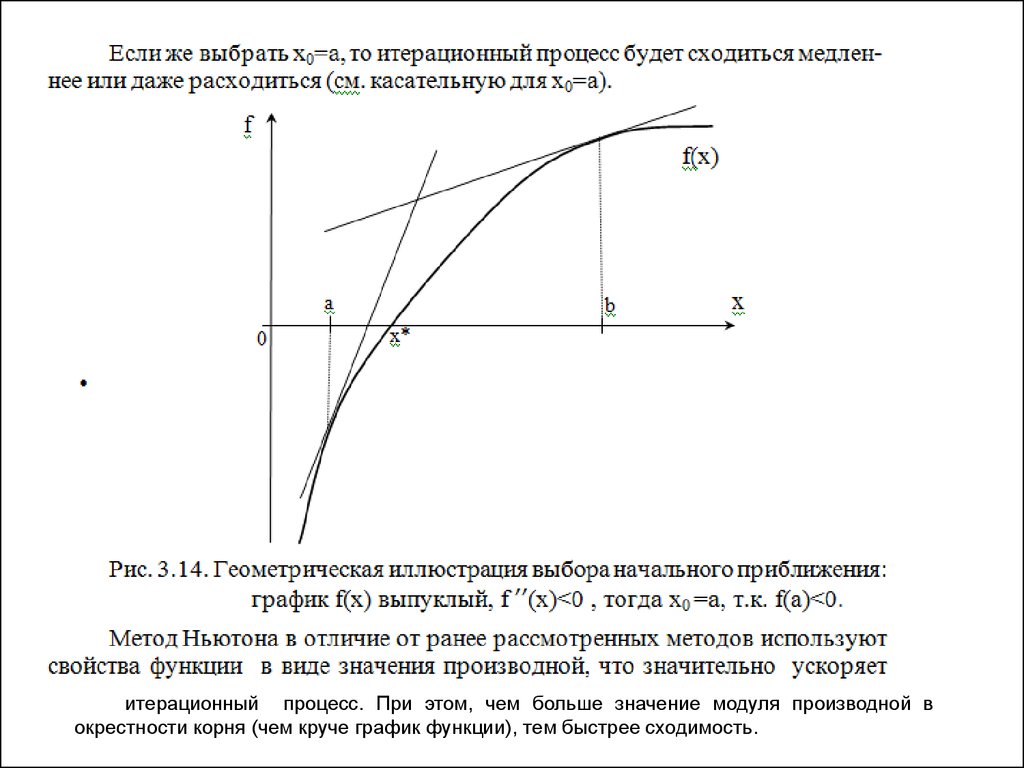
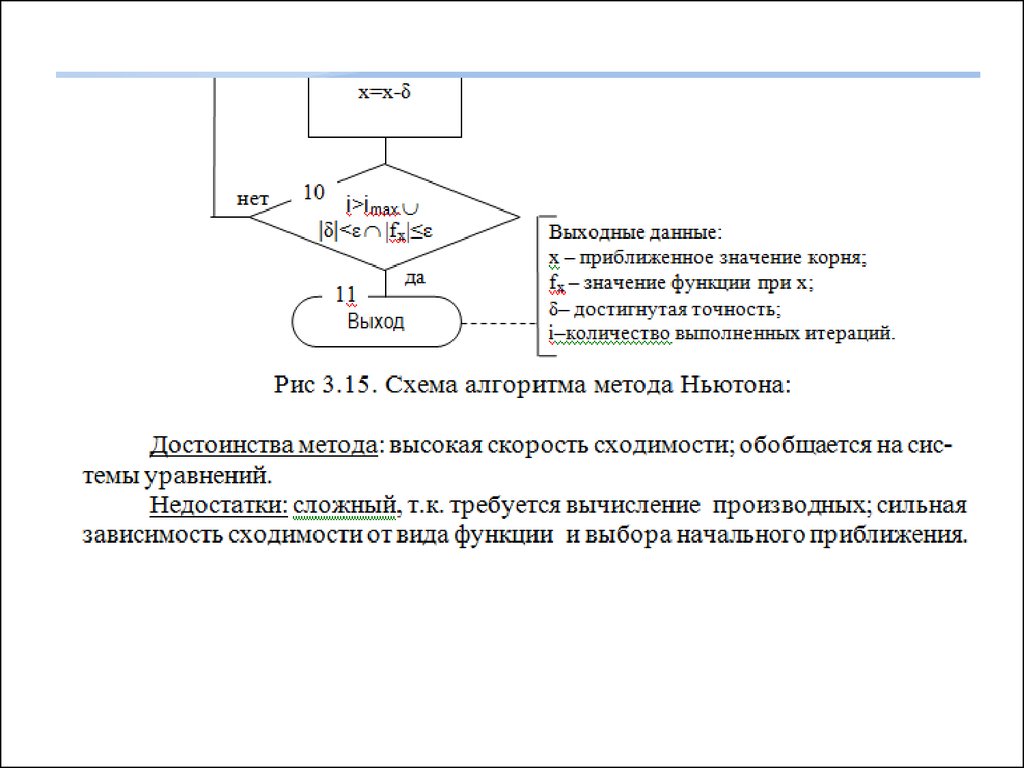
итерационный процесс. При этом, чем больше значение модуля производной вокрестности корня (чем круче график функции), тем быстрее сходимость.





































 Математика
Математика








