Похожие презентации:
Приближенные решения алгебраических и трансцендентных уравнений
1. Приближенные решения алгебраических и трансцендентных уравнений
2. Постановка задачи
Рассмотрим способы решениянелинейных уравнений с одним
неизвестным. Каждое такое уравнение
можно представить в виде:
f(x)=0
(1)
Опр.1 Число t называется корнем уравнения
(1) или нулем функции f, если при
подстановке его вместо х уравнение
превращается в верное равенство
3.
При решении любого уравнения необходимо:1.Установить, имеет ли оно действительные
корни и их количество;
2. Вычислить корни точно, если это возможно и
имеет смысл, или приближенно с заданной
степенью точности.
Опр.2. Поиск приближенного значения корня с
точностью до заданного достаточно малого числа
ε>0 называется уточнением корня. Задача уточнения
будет решена, если найдется число х* такое, что
׀t-x*≤ ׀ε. Тогда t≈ х* с точностью до ε
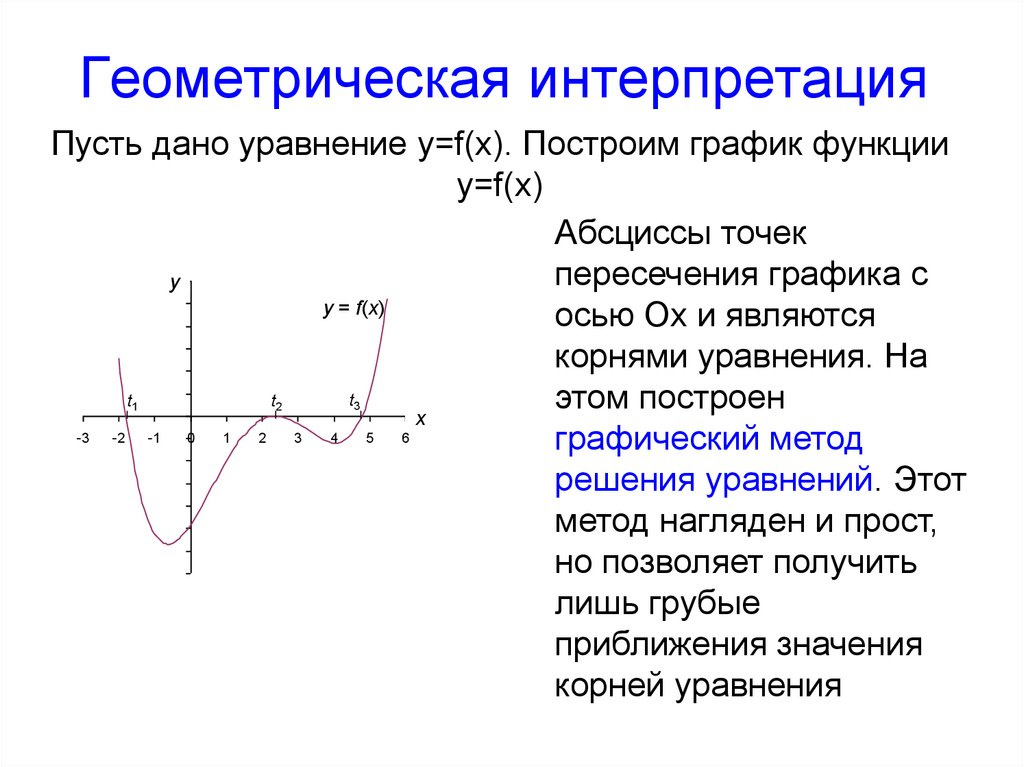
4. Геометрическая интерпретация
Пусть дано уравнение y=f(x). Построим график функцииy=f(x)
Абсциссы точек
пересечения графика с
y
y = f(x)
осью Ох и являются
корнями уравнения. На
t
t
t
этом построен
x
-3
-2
-1
0
1
2
3
4
5
6
графический метод
решения уравнений. Этот
метод нагляден и прост,
но позволяет получить
лишь грубые
приближения значения
корней уравнения
1
2
3
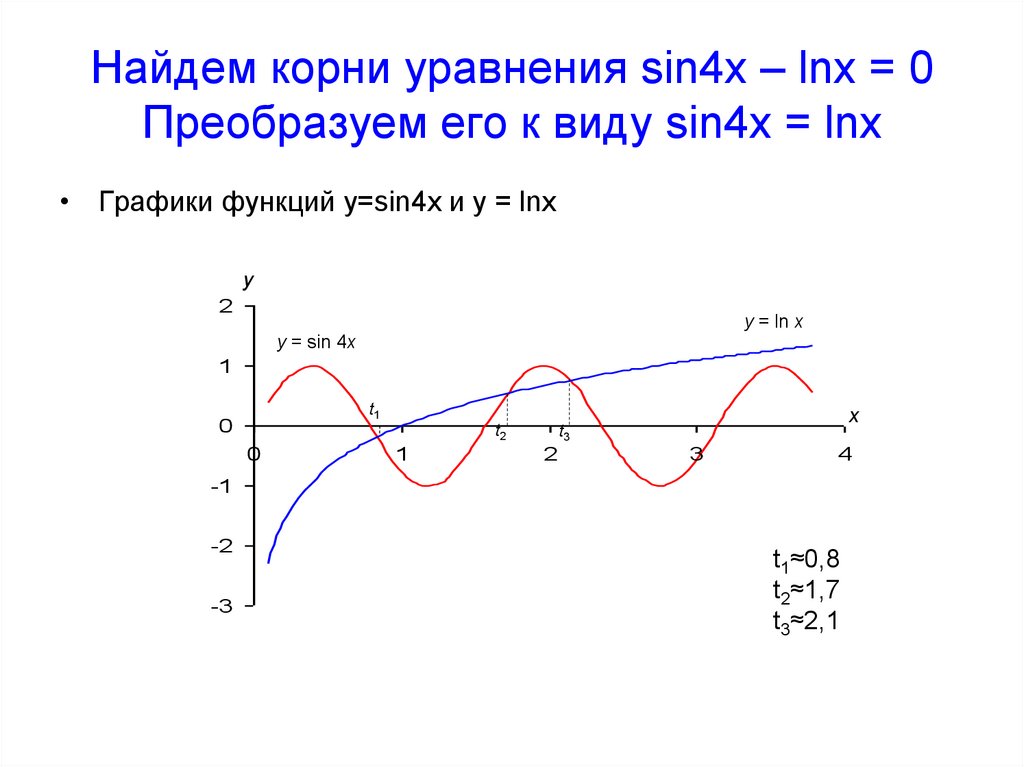
5. Найдем корни уравнения sin4x – lnx = 0 Преобразуем его к виду sin4x = lnx
• Графики функций у=sin4x и у = lnxy
2
y = ln x
y = sin 4x
1
t1
0
t2
0
1
x
t3
2
3
4
-1
-2
-3
t1≈0,8
t2≈1,7
t3≈2,1
6.
Процесс нахожденияприближенных корней уравнения
разбивается на два этапа:
1.Отделение корней
2. Уточнение корней до заданной
степени точности
7. Отделение корней
Опр.3 Отделение корней- это определение ихналичия, количества и нахождение для каждого
из них достаточно малого отрезка [a,b],
которому он принадлежит
Теорема (о единственности корня). Если
функция f(x) определена, непрерывна,
монотонна на отрезке [a,b] и принимает на
концах отрезка значения разных знаков, т.е
f(a)f(b)<0, то существует единственная точка
t (a,b), в которой значение функции равно
нулю
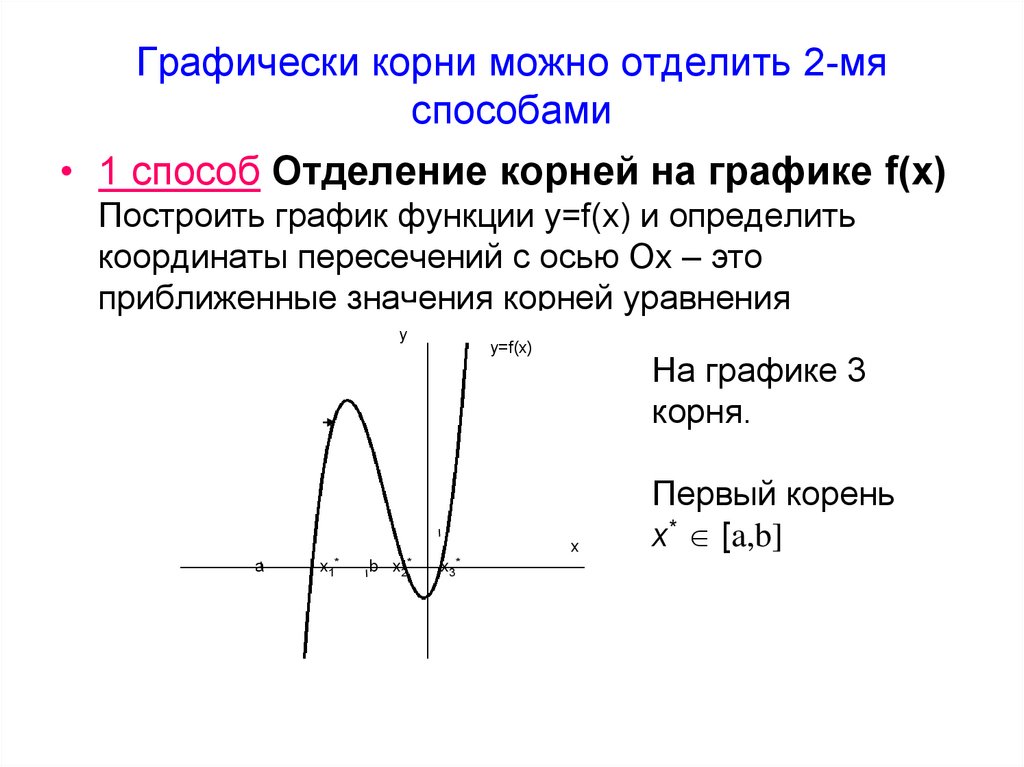
8. Графически корни можно отделить 2-мя способами
• 1 способ Отделение корней на графике f(x)Построить график функции y=f(x) и определить
координаты пересечений с осью Ох – это
приближенные значения корней уравнения
y
y=f(x)
На графике 3
корня.
x
a
x1*
b
x2*
x3*
Первый корень
x* [a,b]
9. 2 способ Отделение корней по графикам функций (x) и (x).
2 способ Отделение корней по графикам функций(x) и (x).
Преобразовать f(x)=0 к виду (x) = (x), где (x) и (x) –
элементарные функции, и определить абсциссу
пересечений графиков этих функций.
y
y= (x)
y= (x)
На графике 2 корня.
Первый корень
x1* [a,b]
x
a
x1*
b
x2*
10. Пример. Отделить корни уравнения x5 – 4x2 + x+1 = 0.
Функция f(x)= x5 – 4x2 + x +1 определена и непрерывна на всейдействительной оси, а также
lim f ( x) , lim f ( x) .
x
x
Следовательно уравнение имеет по крайней мере один корень.
Составим таблицу знаков функции f(x):
x
Sign f(x)
-
-
-1
-
0
+
1
-
2
+
+
+
Уравнение x5 – 4x2 + x+1 = 0 имеет три действительных корня:
t1 [-1; 0], t2 [0; 1], t3 [1; 2].
11. Пример 2 Отделить корни уравнения .
2 cos x x 2 3x 2 03
Уравнение удобно представить в виде:
2 cos x x 2 3x 2
3
и построить графики функций
x 2 cos x
3
g x x 2 3x 2
12. Уравнение имеет два корня: t1[0,5; 1], t2[2,5; 3].
Уравнение имеет два корня:t1 [0,5; 1], t2 [2,5; 3].
φ(x)=2cos(x+π/3)
1
t1 1
2
t2
3
-1
-2
g(x)= -x2+3x-2
13. Блок-схема алгоритма отделения корней уравнения f(x)=0
14. Метод половинного деления
Пусть дано уравнение f(x)=0.Будем считать, что отделение корней произведено и на отрезке [a; b]
расположен один корень t. Требуется найти приближенное
значение корня с точностью до , где – достаточно малое
положительное число.
Разделим [a; b] пополам точкой с и вычислим f(c). Проверим
следующие условия:
• Если f(c)=0, то c – корень. t=c.
• Если f(a) f(c)<0, то корень лежит в интервале [a; c].
• Если f(c) f(b)<0, то корень лежит в интервале [b; c].
Выберем ту половину отрезка, на концах которой функция
принимает значения разных знаков, и обозначим ее [a1; b1]. Затем
отрезок [a1; b1] делим пополам точкой и проводим аналогичные
рассуждения. Получится либо точный корень t=c1, либо отрезок
[a2; b2] со свойством f(a2) f(b2)<0. И так далее.
15. Геометрическая интерпретация метода половинного деления
yy=f(x)
a1
a
c
b1
t
c1
b
x
16. Если на каком-то шаге обнаружится точный корень (что практически маловероятно), то процесс деления пополам закончится
нахождением точного значения. Если нет, тополучится бесконечная последовательность вложенных
отрезков
• Для того, чтобы найти приближенное значение корня с
точностью до >0, необходимо остановить итерационный
процесс половинного деления на таком шаге n, где bn – an 2 .
Тогда за приближенное значение корня можно взять величину
с точностью , так как
*
* an bn
x
2
t x
t x
*
2
t
x*
an
bn
x
17. Количество итераций n, требуемых для достижения заданной точности ε можно оценить заранее из соотношения
b an
n
2
ln
b a
ln 2
или
b a
n 1,4427 ln
1
18. Замечания:
1.2.
3.
4.
5.
6.
7.
Метод половинного деления дает простой и удобный алгоритм
уточнения корней с любой наперед заданной степенью точности.
Он требует от функции f легко проверяемых свойств:
непрерывности на отрезке изоляции корня и разных знаков
значений на его концах. Это обеспечивает его применимость к
обширному классу уравнений.
Скорость приближения к корню зависит лишь от длины
начального отрезка [a; b] и заданной точности и не зависит от
функции f.
На каждом шаге итерации погрешность приближенного значения
корня уменьшается ровно вдвое (и только). Вследствие этого
увеличение точности всегда сопровождается пропорциональным
ростом объема вычислений.
Если на отрезке, на концах которого непрерывная функция f
принимает значения разных знаков, содержится несколько
корней, то процесс половинного деления сойдется к одному из
них (к какому заранее неизвестно).
Метод неприменим к корням четной кратности.
Для корней нечетной высокой кратности метод слабо устойчив к
ошибкам округления, возникающим при вычислении f(x).
Метод половинного деления не обобщается на системы
уравнений.
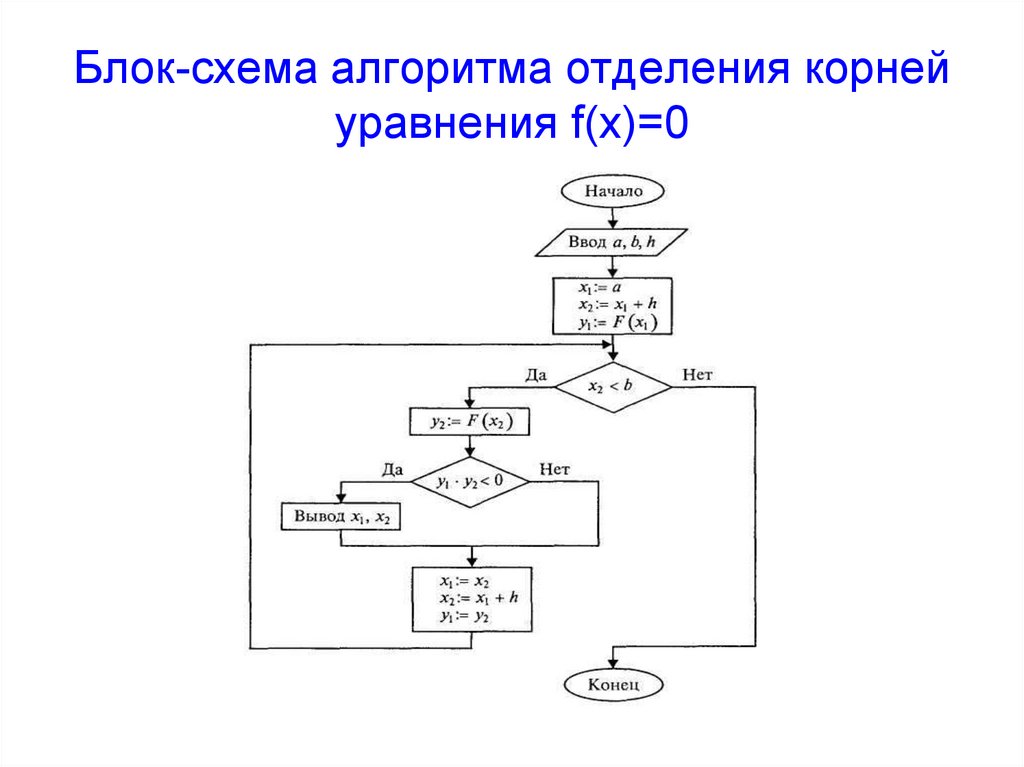
19. Блок-схема алгоритма уточнения корня уравнения f(x)=0 на отрезке [a;b] с точностью методом половинного деления
Блок-схема алгоритма уточнения корня уравнения f(x)=0 наотрезке [a;b] с точностью методом половинного деления








![Уравнение имеет два корня: t1[0,5; 1], t2[2,5; 3]. Уравнение имеет два корня: t1[0,5; 1], t2[2,5; 3].](https://cf3.ppt-online.org/files3/slide/1/1hkz6HqJo4ramIgW5FD9X20lGpvSBTLdbNtEw7/slide-11.jpg)





![Блок-схема алгоритма уточнения корня уравнения f(x)=0 на отрезке [a;b] с точностью методом половинного деления Блок-схема алгоритма уточнения корня уравнения f(x)=0 на отрезке [a;b] с точностью методом половинного деления](https://cf3.ppt-online.org/files3/slide/1/1hkz6HqJo4ramIgW5FD9X20lGpvSBTLdbNtEw7/slide-18.jpg)
 Математика
Математика








