Приближенное решение алгебраических и трансцендентных уравнений

1. Приближенное решение алгебраических и трансцендентных уравнений

Лекция 2

2. Алгебраические и трансцендентные уравнения

При решении практических задач часто
приходится сталкиваться с решением
уравнений.
Всякое уравнение с одним неизвестным в
общем виде можно представить так:
F(x)=0

3. Алгебраические и трансцендентные уравнения

Такие уравнения могут быть алгебраическими
или трансцендентными.
Примеры алгебраических уравнений:
2x3 -1,5x2 +1=0,
x3 +2√x -4=0,
Примеры трансцендентных уравнений:
sinx - ex +3=0,
x2 + ln x=0.

4. Вспомним:

Решение уравнения с одним неизвестным
заключается в отыскании корней, т. е. тех
значений х, которые обращают уравнение в
тождество. Корни уравнения могут быть
действительными или комплексными.
Решить уравнение – это значит
установить, имеет ли оно корни,
сколько корней,
и найти значение корней с заданной
точностью.

5.

Задача численного нахождения
действительных и комплексных корней
уравнения обычно состоит из двух этапов:
отделение корней, т.е. нахождение
достаточно малых окрестностей
рассматриваемой области, в которых
находится одно значение корня,
и уточнение корней, т.е. вычисление корней
с заданной степенью точности в некоторой
окрестности.

6.

Наиболее распространенными на практике
численными методами решения уравнений
являются:
метод дихотомии (метод деления отрезка
пополам);
метод хорд;
метод касательных (метод Ньютона);
метод итераций.
Применение того или иного метода для
решения уравнения зависит от числа корней,
задания исходного приближения и поведения
функции F(x).

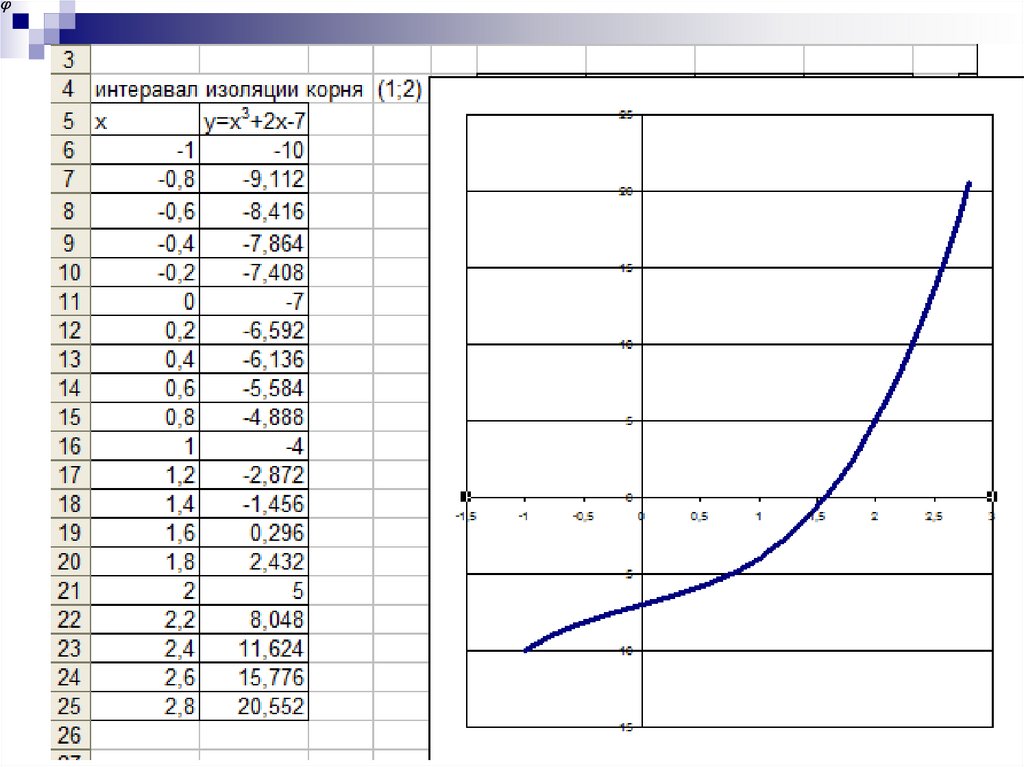
7. Отделение корней

Первый этап численного решения уравнения
f(x)=0 состоит в отделении корней, т.е. в
установлении “тесных” промежутков, содержащих
только один корень.
Корень уравнения f(х) = 0 считается
отделенным на отрезке [a,b], если на этом отрезке
уравнение f(х) = 0 не имеет других корней.
Отделить корни – это значит разбить всю
область допустимых значений на отрезки, в каждом
из которых содержится один корень.
Отделение корней можно произвести двумя
способами – графическим и аналитическим.

8. Графический метод отделения корней

При графическом методе отделения корней
поступают так же, как и при графическом
методе решения уравнений.
Графический метод отделения корней не
обладает большой точностью. Он дает
возможность грубо определить интервалы
изоляции корня. Далее корни уточняются
одним из озвученных методов

9. Графический метод отделения корней

Все члены уравнения разбивают
на две группы, одну из них
записывают в левой части уравнения,
а другую в правой, т. е. представляют
его в виде f(х) = g(х).
После этого строят графики двух
функций у = f(х) и у = g(х). Абсциссы
точек пересечения графиков этих
двух функций и служат корнями
данного уравнения. Пусть точка
пересечения графиков имеет
абсциссу х0, ординаты обоих
графиков в этой точке равны между
собой, т. е. f(х0) = g(х0). Из этого
равенства следует, что х0 – корень
уравнения
у
y=g(x)
x0
х
y=f(x)

10. Пример 1. Решить графически уравнение х3 - 2x2 + 2х - 1 = 0.

Представим данное
уравнение в виде:
х3= 2x2 + 2х–1
и построим графики функций
у = х3 и у = 2x2 + 2х – 1.
Найдем абсциссу точки
пересечения этих графиков;
получим х = 1

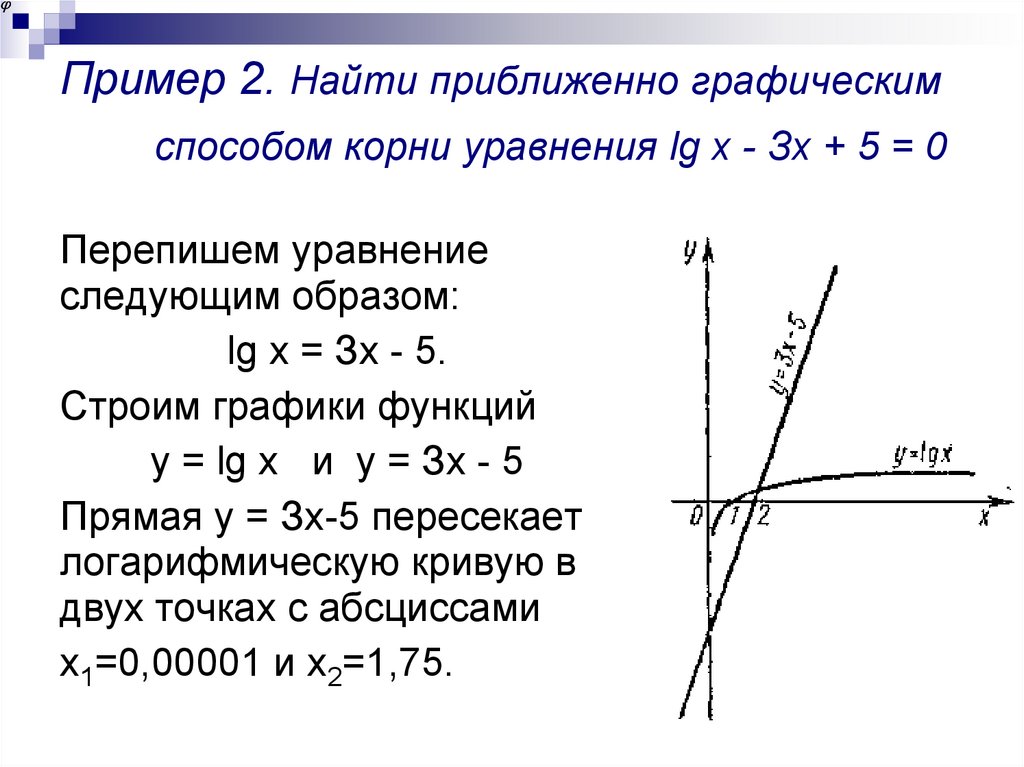
11. Пример 2. Найти приближенно графическим способом корни уравнения lg х - Зх + 5 = 0

Перепишем уравнение
следующим образом:
lg х = Зх - 5.
Строим графики функций
у = lg х и у = Зх - 5
Прямая у = Зх-5 пересекает
логарифмическую кривую в
двух точках с абсциссами
x1=0,00001 и x2=1,75.

12.

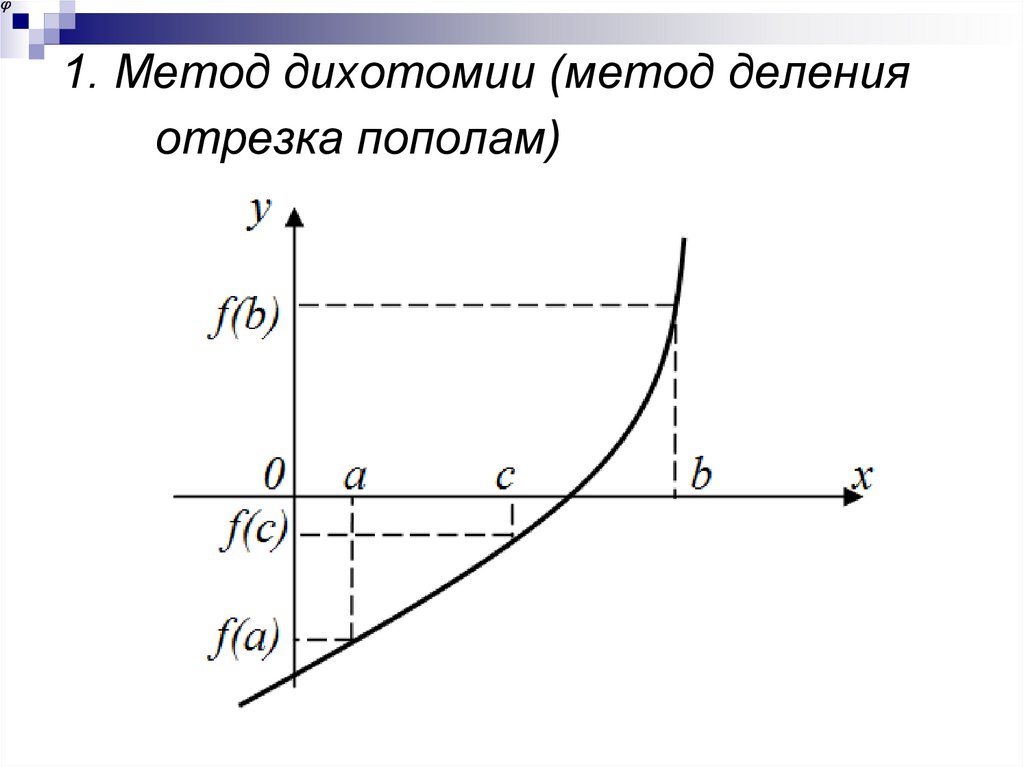
13. 1. Метод дихотомии (метод деления отрезка пополам)

Этот метод можно использовать когда нам
предположительно или точно известны
границы отрезка, содержащего корень и на этих
границах f(x) принимает значения разных
знаков, тогда по теореме о достаточных
условиях существования корня на заданном
отрезке существует хотя бы один корень.

14. 1. Метод дихотомии (метод деления отрезка пополам)

Алгоритм:
Делим отрезок [a; b] пополам.
Определяем, на границах какой из частей
первоначального интервала функция f(x)
меняет знак.
Полученный интервал снова делим на две
части и т.д.
Такой процесс продолжаем до тех пор, пока
не перестанут изменяться сохраняемые в
ответе десятичные знаки.

15. 1. Метод дихотомии (метод деления отрезка пополам)

16. 2. Метод хорд

Рассмотрим график функции у= f(x). Пусть
f(а)<0 и f(в)>0.
Точки графика А[a;f(a)] и В[b;f(b)] соединим
хордой.
За приближенное значение искомого корня
примем абсциссу х1 точки пересечения хорды
АВ с осью Ох .
Это приближенное значение находится по
формуле
, где x1 (a;b)

17. 2. Метод хорд

Пусть, например, f(x1)<0, тогда за новой (более
узкий) промежуток изоляции корня принять [x1,b].
Соединив точки А1[x1;f(x1)] и В[b;f(b)] , получим в
точке пересечения хорды с осью Ох второе
приближение x2, которое вычислим по формуле:
и т.д.
Последовательность чисел a1, x1, x2,…стремится к
искомому корню уравнения f(x)=0 .Вычисление
приближенных значений корней уравнения следует
вести до тех пор, пока не будет достигнута заданная
степень точности)

18. 2. Метод хорд

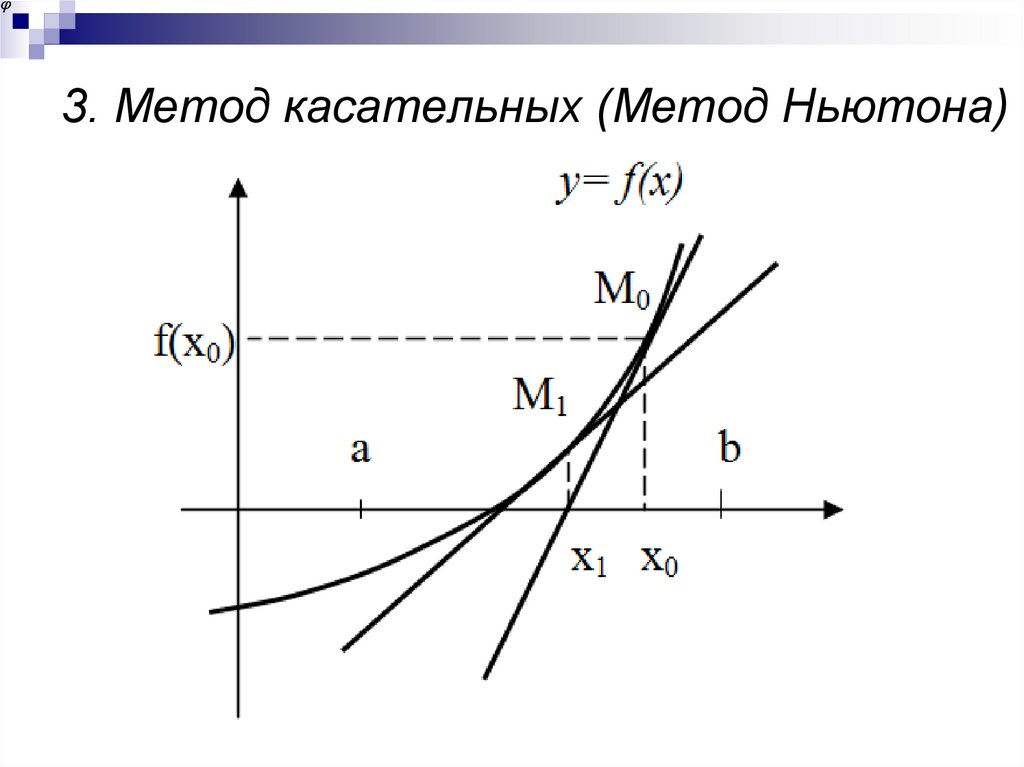
19. 3. Метод касательных (Метод Ньютона)

Пусть действительный корень уравнения
f(x)=0 изолирован на отрезке [а,в]. Будем
предполагать, что все ограничения,
сформулированные выше относительно f(x),
сохраняют силу и в этом случае.
Выделяем на отрезке [а,в] такое число x0,
при котором f(x0) имеет тот же знак, что и
f’’(x0) т.е. f(x0)*f’’(x0)>0 (в частности , за x0
может быть принят тот из концов отрезка [а,в],
в котором соблюдено это условие). Проведем в
точке Мо[x0, f(x0)] касательную к кривой y=f(x) .

20. 3. Метод касательных (Метод Ньютона)

За приближенное значение корня примем
абсциссу точки пересечения этой касательной
с осью Ох. Это приближенное значение корня
находится по формуле:
Применив этот прием вторично в точке
M1[x1; f(x1)], найдем
и т.д.
Полученная т.об. последовательность x0, x1,
x2,… имеет своим пределом искомый корень.

21. 3. Метод касательных (Метод Ньютона)

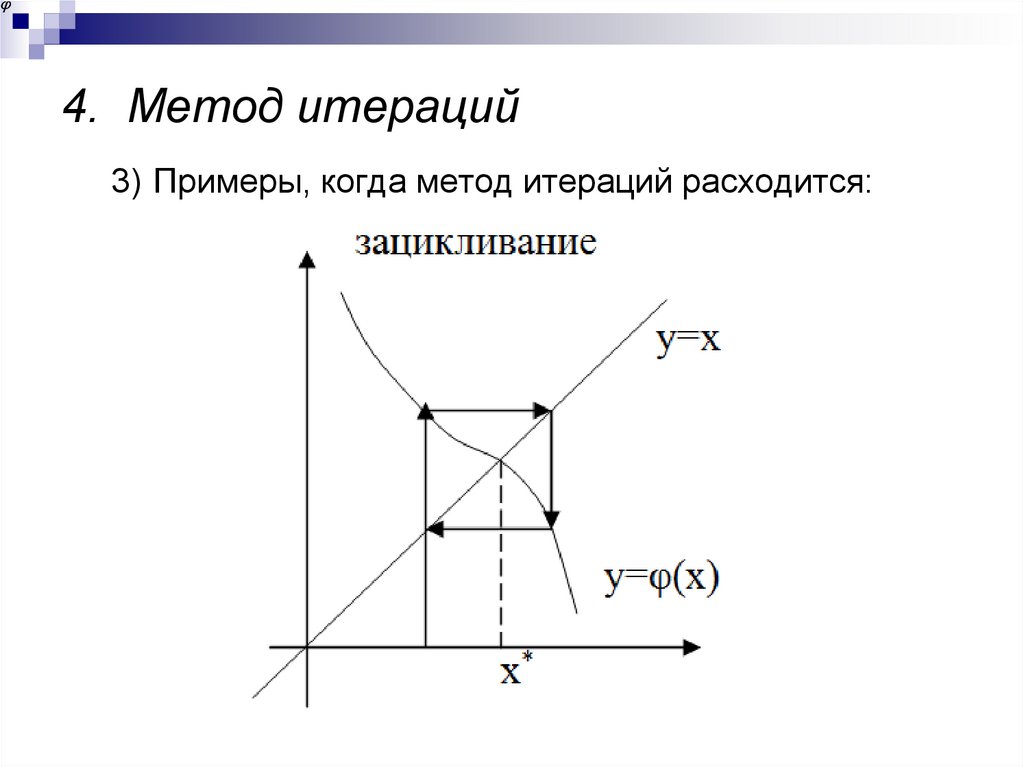
22. 4. Метод итераций

Если данное уравнение приведено к виду
всюду на отрезке [а,в], на котором исходное
уравнение имеет единственный корень, то
исходя из некоторого начального значения x0,
принадлежащего отрезку [а,в], можно построить
такую последовательность:
Пределом этой последовательности
является единственный корень уравнения
f(x)=0 на отрезке [а,в].

23. 4. Метод итераций

1) односторонняя сходимость:

24. 4. Метод итераций

2) двухсторонняя сходимость:

25. 4. Метод итераций

3) Примеры, когда метод итераций расходится:

26. 4. Метод итераций

3) Примеры, когда метод итераций расходится: