Похожие презентации:
Вектори в просторі. Рівень стандарту (10 клас)
1. Вектори в просторі. Рівень стандарту. 10 клас.
2.
1844 -1850 р.р. - основи векторного числення булизакладені дослідженнями англійського математика
У.Гамільтона і німецького математика Г. Грассмана по
гіперкомплексних числах.
3.
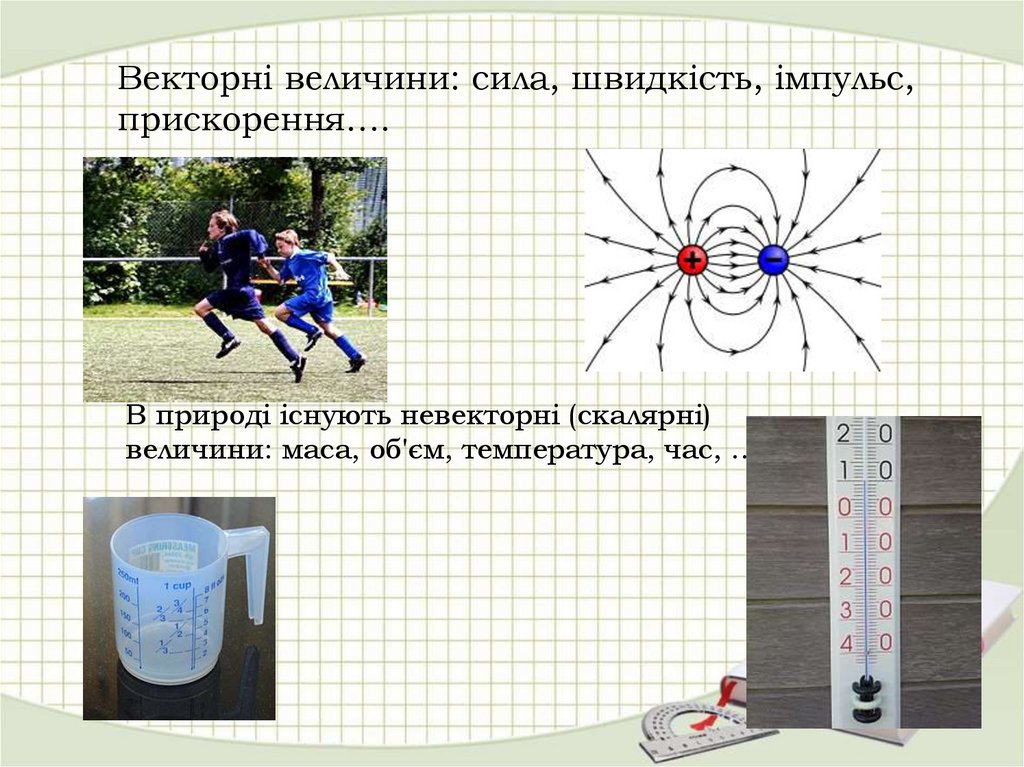
Векторні величини: сила, швидкість, імпульс,прискорення….
В природі існують невекторні (скалярні)
величини: маса, об'єм, температура, час, …..
4.
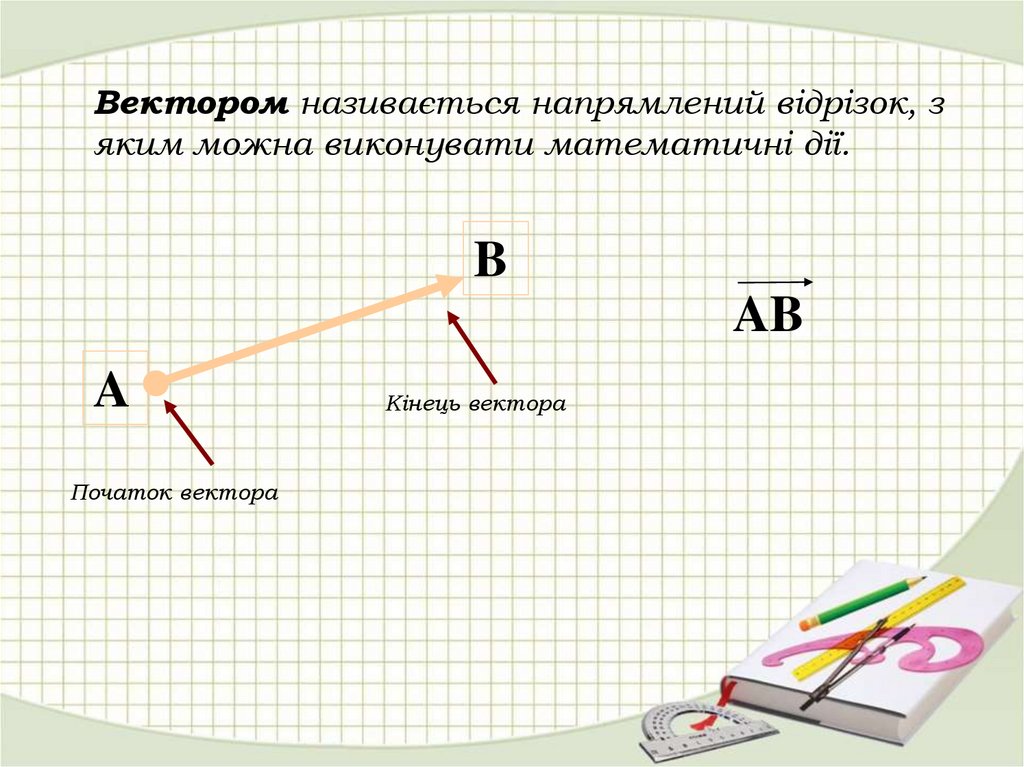
Вектором називається напрямлений відрізок, зяким можна виконувати математичні дії.
B
AB
A
Початок вектора
Кінець вектора
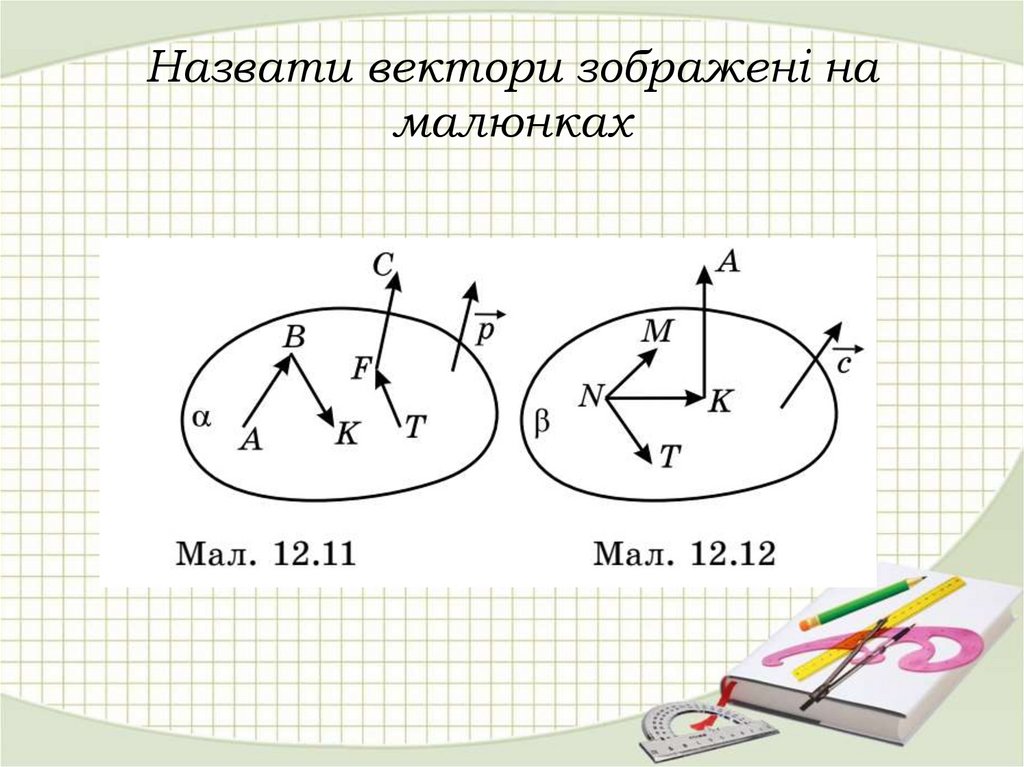
5. Назвати вектори зображені на малюнках
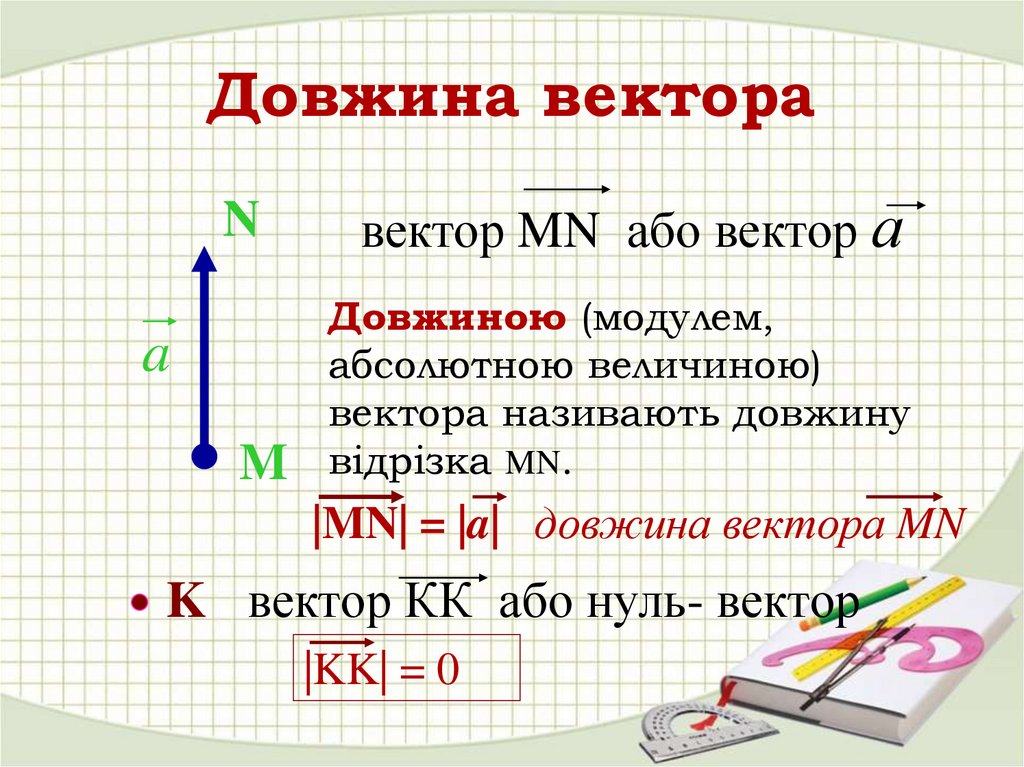
6. Довжина вектора
Na
M
вектор MN або вектор а
Довжиною (модулем,
абсолютною величиною)
вектора називають довжину
відрізка MN.
|MN| = |a| довжина вектора MN
K вектор КК або нуль- вектор
|KK| = 0
7.
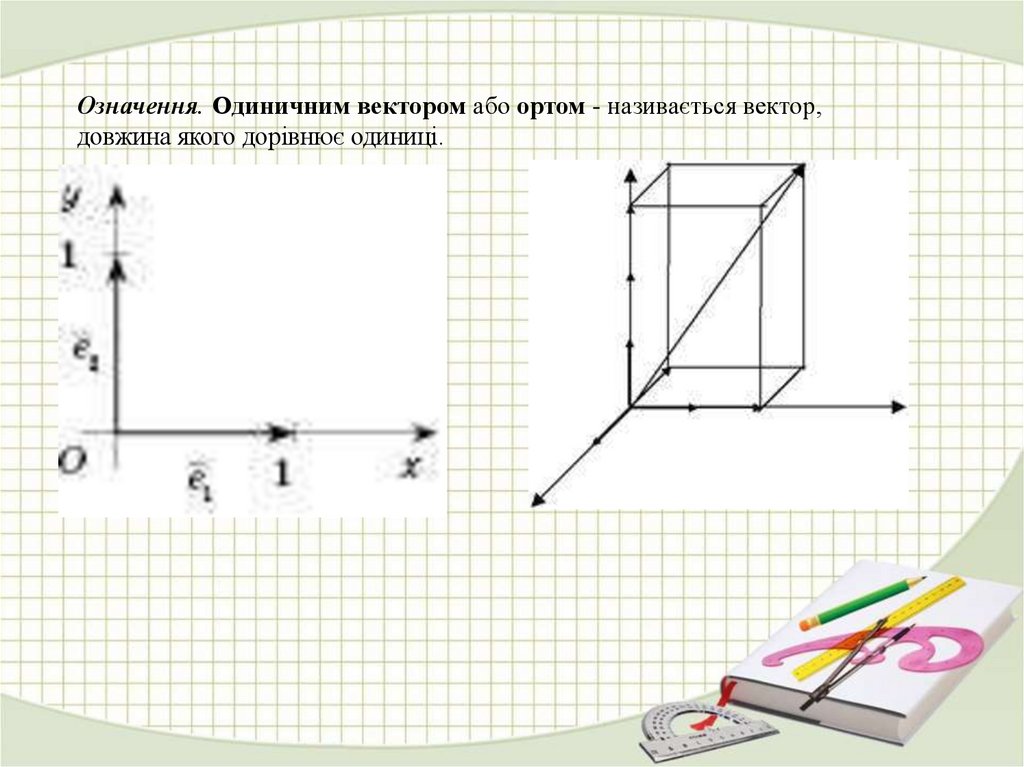
Означення. Одиничним вектором або ортом - називається вектор,довжина якого дорівнює одиниці.
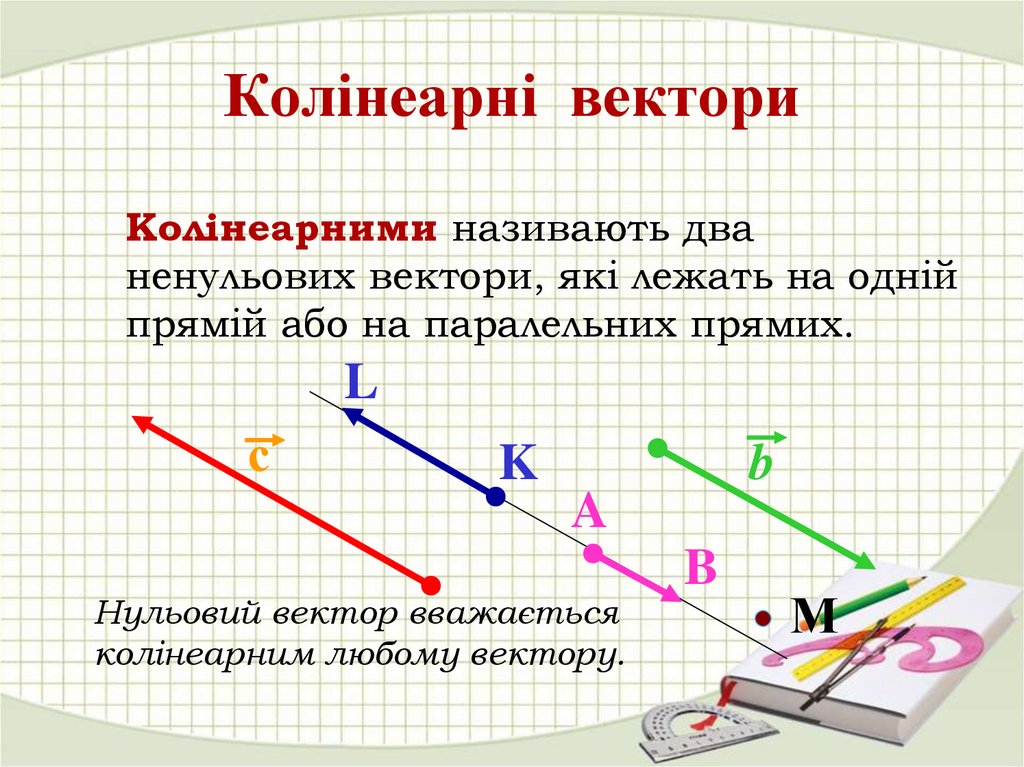
8. Колінеарні вектори
Колінеарними називають дваненульових вектори, які лежать на одній
прямій або на паралельних прямих.
L
с
K
b
A
Нульовий вектор вважається
колінеарним любому вектору.
B
М
9.
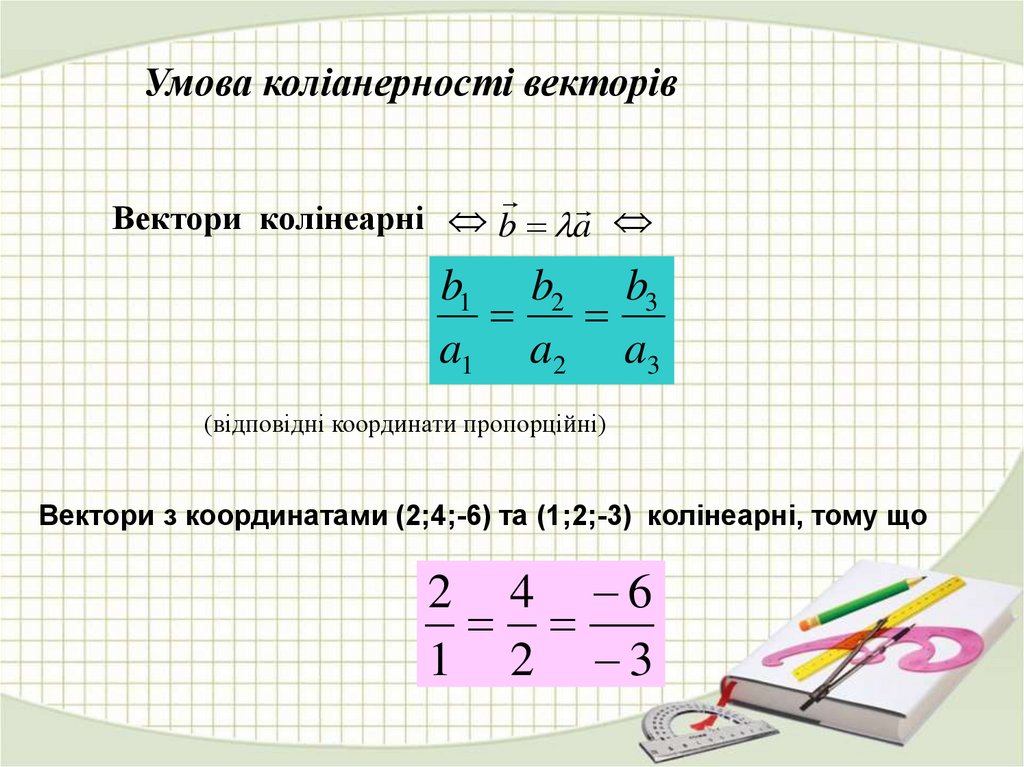
Умова коліанерності векторівВектори колінеарні b a
b1 b2 b3
a1 a2 a3
(відповідні координати пропорційні)
Вектори з координатами (2;4;-6) та (1;2;-3) колінеарні, тому що
2 4 6
1 2 3
10.
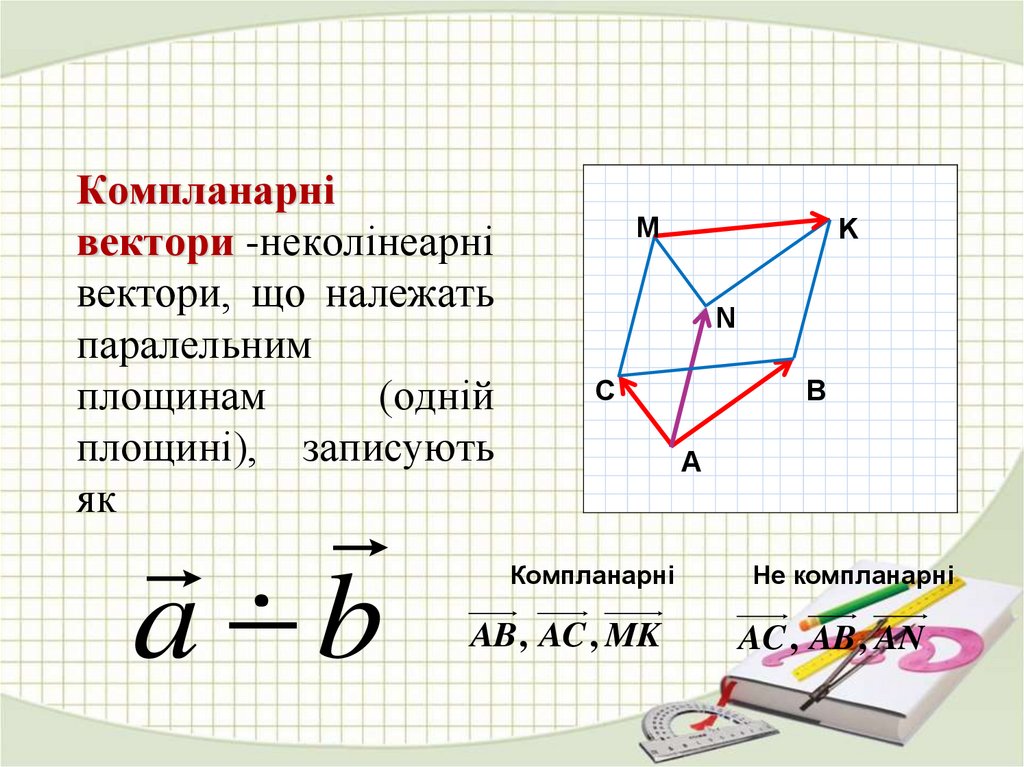
Компланарнівектори -неколінеарні
вектори, що належать
паралельним
площинам
(одній
площині), записують
як
a b
M
K
N
В
C
A
Компланарні
AB, AC , MK
Не компланарні
AC , AB , AN
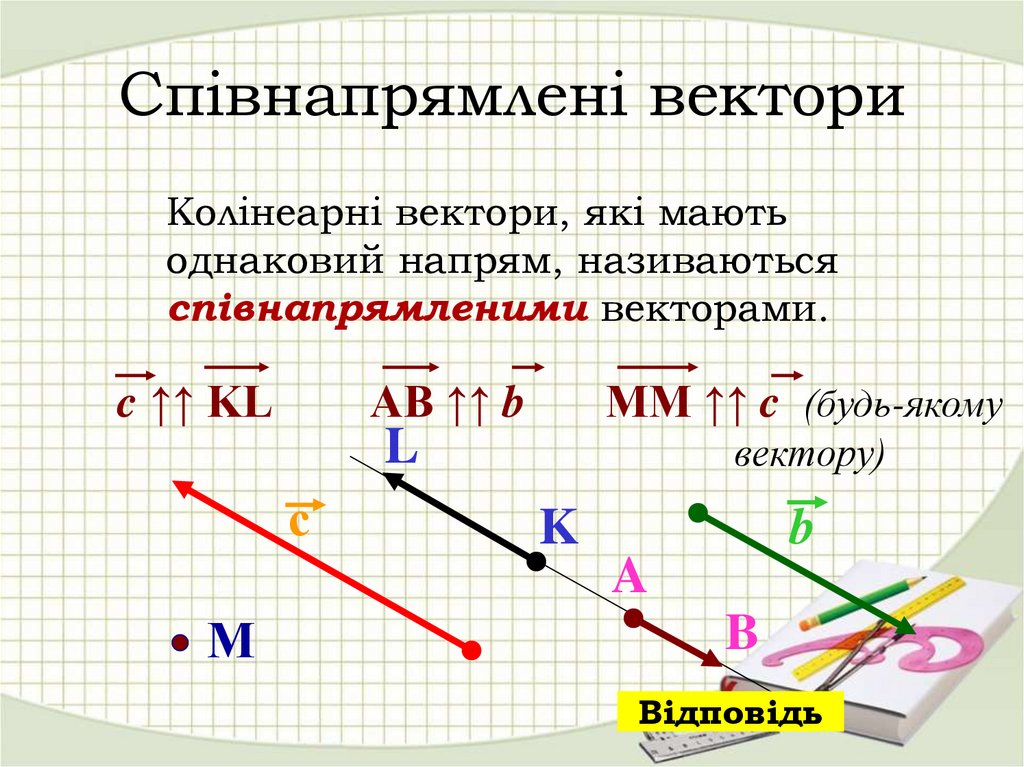
11. Співнапрямлені вектори
Колінеарні вектори, які маютьоднаковий напрям, називаються
співнапрямленими векторами.
c ↑↑ KL
AB ↑↑ b
MM ↑↑ c (будь-якому
L
с
вектору)
K
b
A
М
B
Відповідь
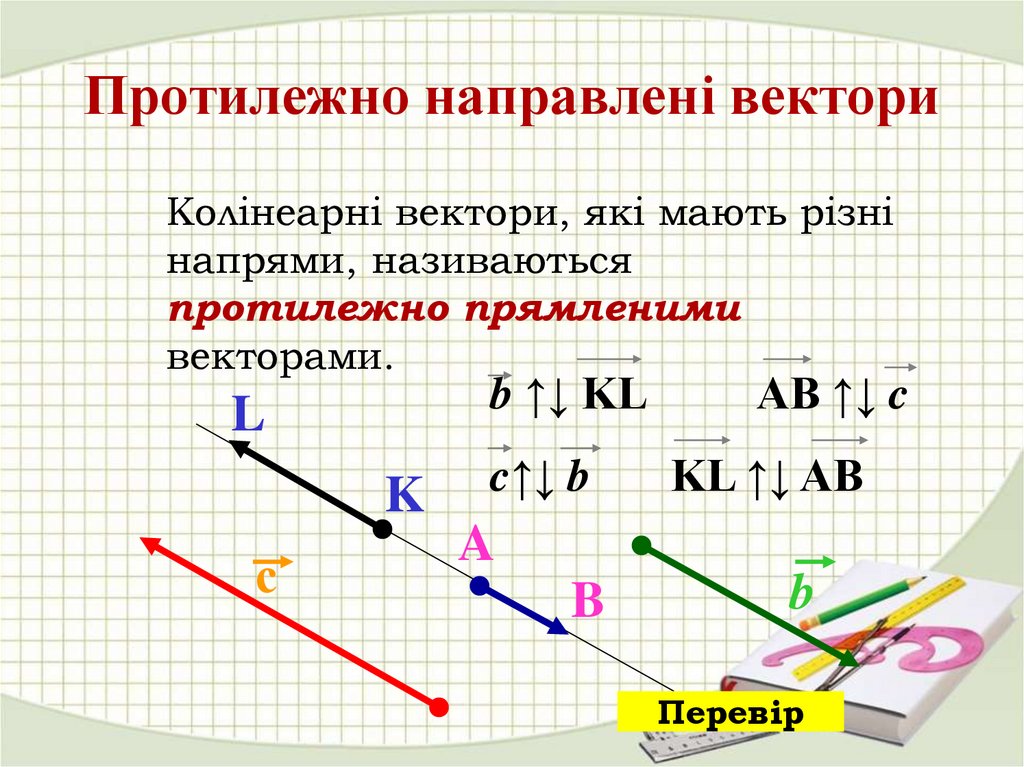
12. Протилежно направлені вектори
Колінеарні вектори, які мають різнінапрями, називаються
протилежно прямленими
векторами.
b ↑↓ KL
L
K
с
c↑↓ b
AB ↑↓ c
KL ↑↓ AB
A
B
b
Перевір
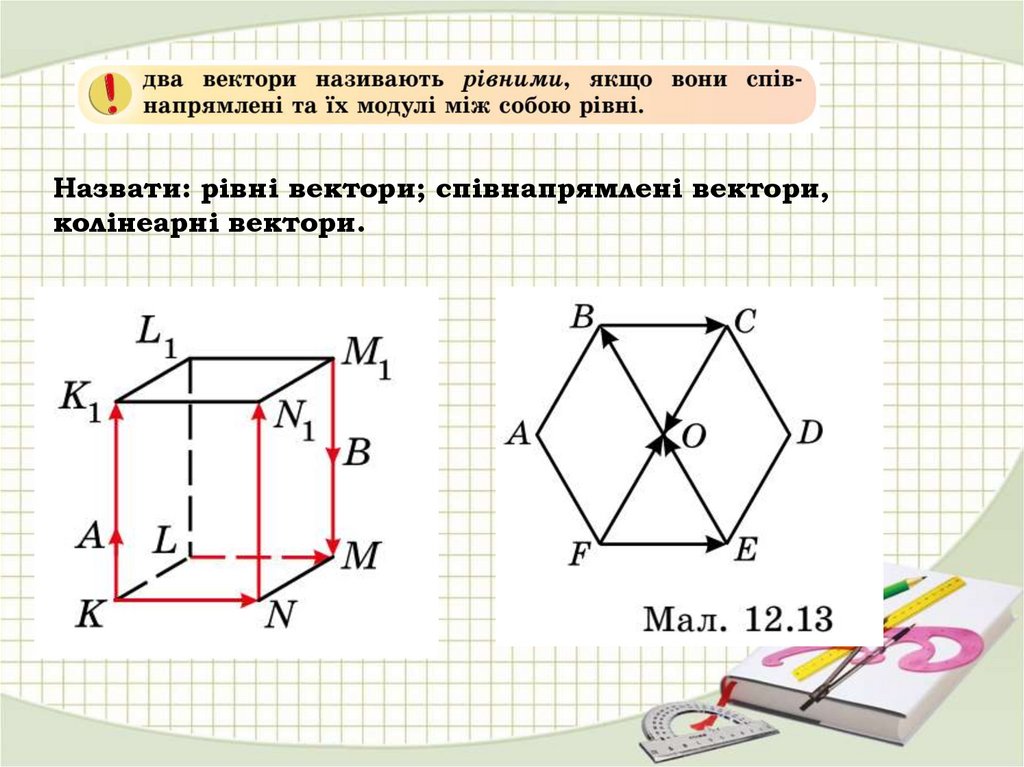
13.
Назвати: рівні вектори; співнапрямлені вектори,колінеарні вектори.
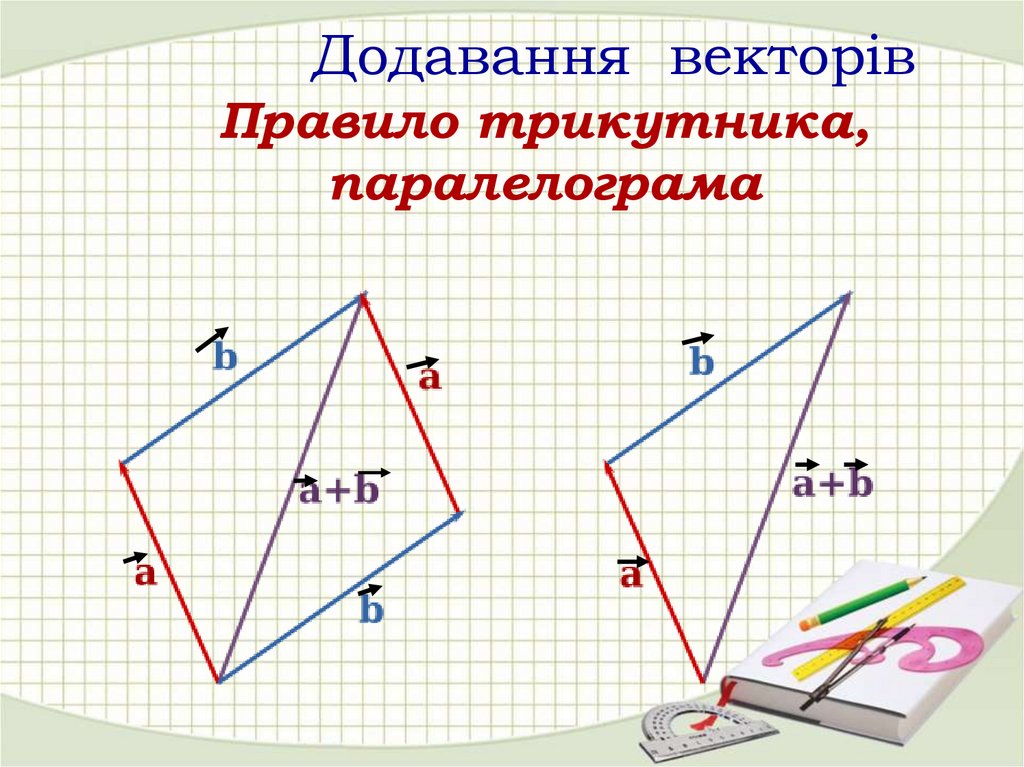
14.
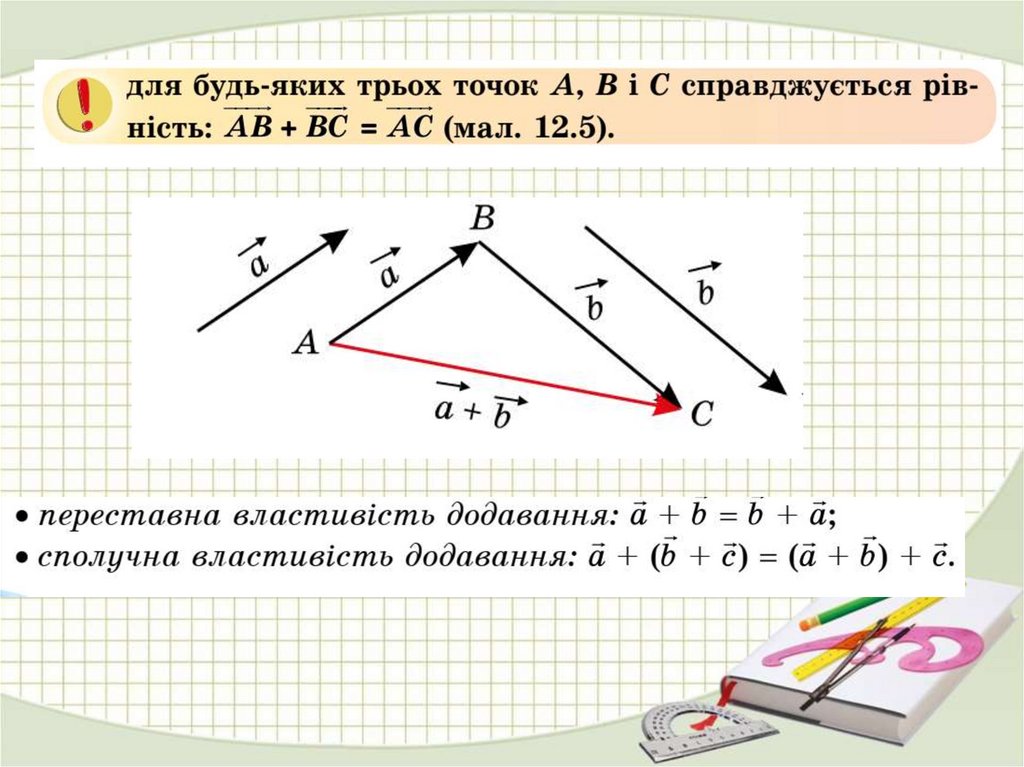
Додавання векторівПравило трикутника,
паралелограма
15.
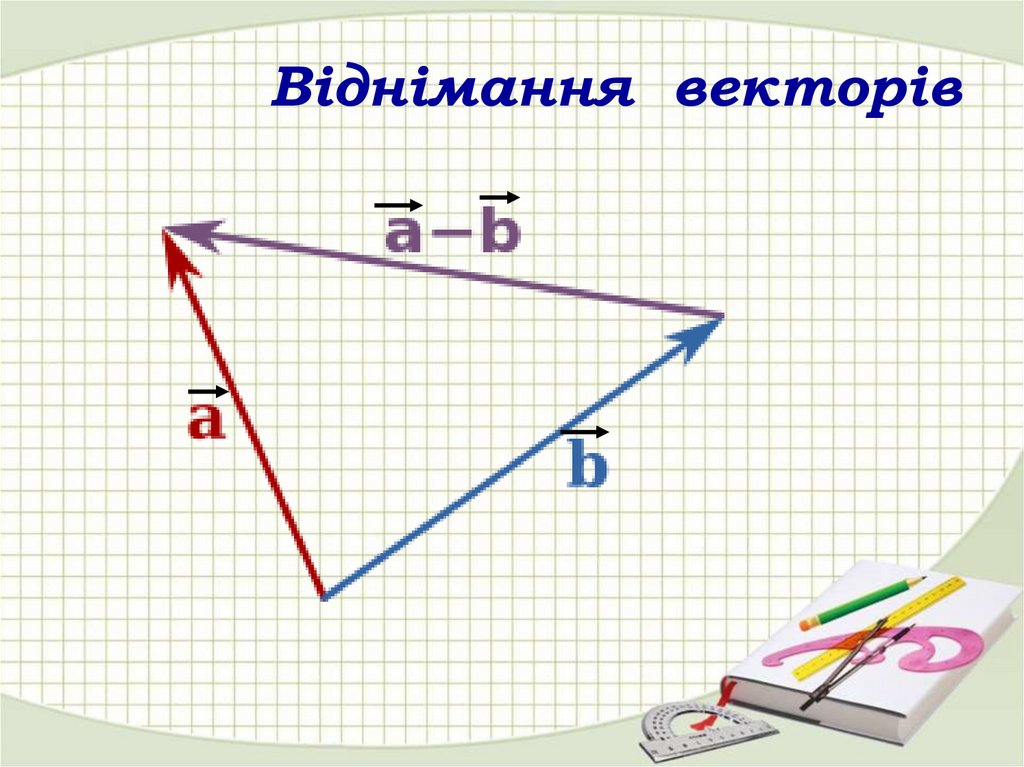
Віднімання векторів16.
KМ
D
a b c
B
А
c
a b
a
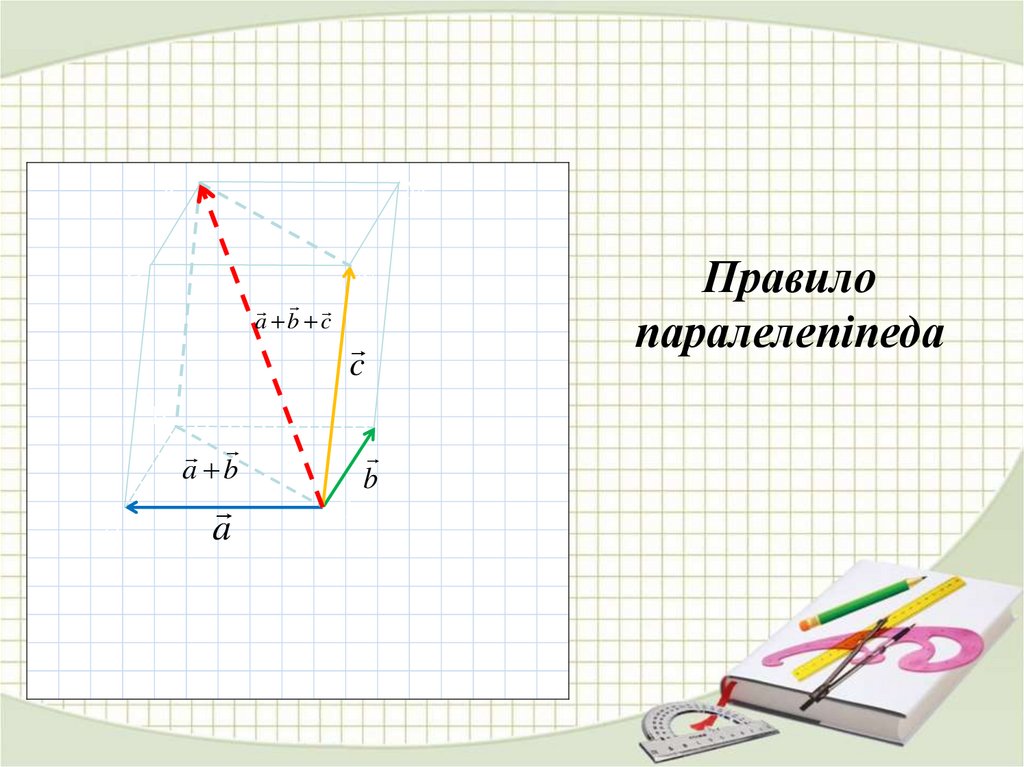
Правило
паралелепіпеда
N
О
b
С
17.
18.
а
b
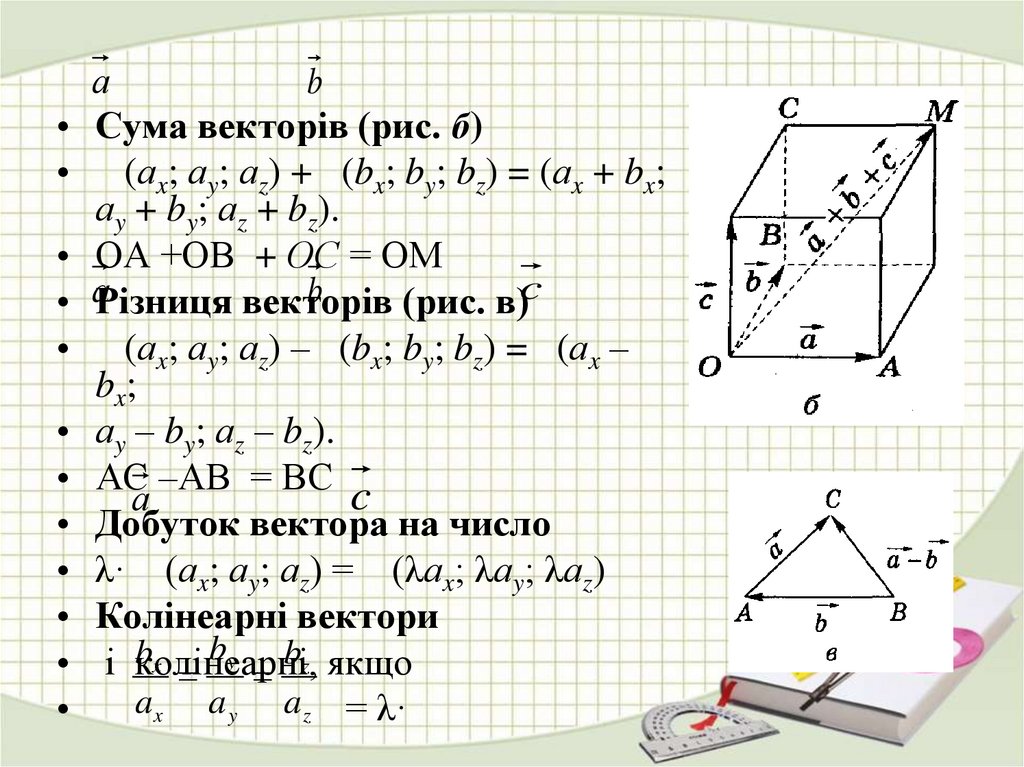
Сума векторів (рис. б)
(аx; аy; аz) + (bx; by; bz) = (аx + bx;
аy + by; аz + bz).
ОА +ОВ + ОС = ОМ
аРізниця векторів
b
(рис. в)c
(аx; аy; аz) – (bx; by; bz) = (аx –
bx;
аy – by; аz – bz).
АС –АВ = ВС
c
а
Добуток вектора на число
λ· (аx; аy; аz) = (λаx; λаy; λаz)
Колінеарні вектори
bx by bz якщо
і колінеарні,
a x a y a z = λ·
19.
Приклад . Існують точки А(2; 0; 1), В(3; 5; 0), С(-1; 2; 3).Знайти координати вектора n 2 AB 3BC.
Розв’язання.
Знайдемо координати векторів:
ВС 1 1; 2 5; 3 - 0 4; 3; 3 .
АВ 3 2; 5 0; 0 1 1; 5; 1 ;
Скориставшись правилами виконання дій над векторами,
заданими координатами, маємо:
3ВС 3 4; 3; 3 12; 9; 9 .
n 2 АВ 3ВС 2; 10; - 2 12; 9; 9 14; 19; 11 .
2 АВ 2 1; 5; 1 2; 10; - 2 ;
20.
• Задача 1. Дано а (-1; 2; -3), b (2; -1; 3).Знайдіть координати векторів
2 а
3b
2 а 3 b
1) 2а (2 ( 1); 2 2; 2 ( 3))
2 а 3 b
1) 2а ( 2; 4; 6)
2) 3b ( 3 2; 3 ( 1); 3 3)
3) 2 а 3 b ( 2 ;4; 6) ( 6;3; 9)
3) 2 а 3 b ( 2 ;4; 6) ( 6;3; 9)
2) 3b ( 6; 3; 9)
3) 2 а 3 b ( 8;7; 15)
3) 2 а 3 b (4;1;3)






 Математика
Математика








