Вектори у просторі

1. вектори У просторі

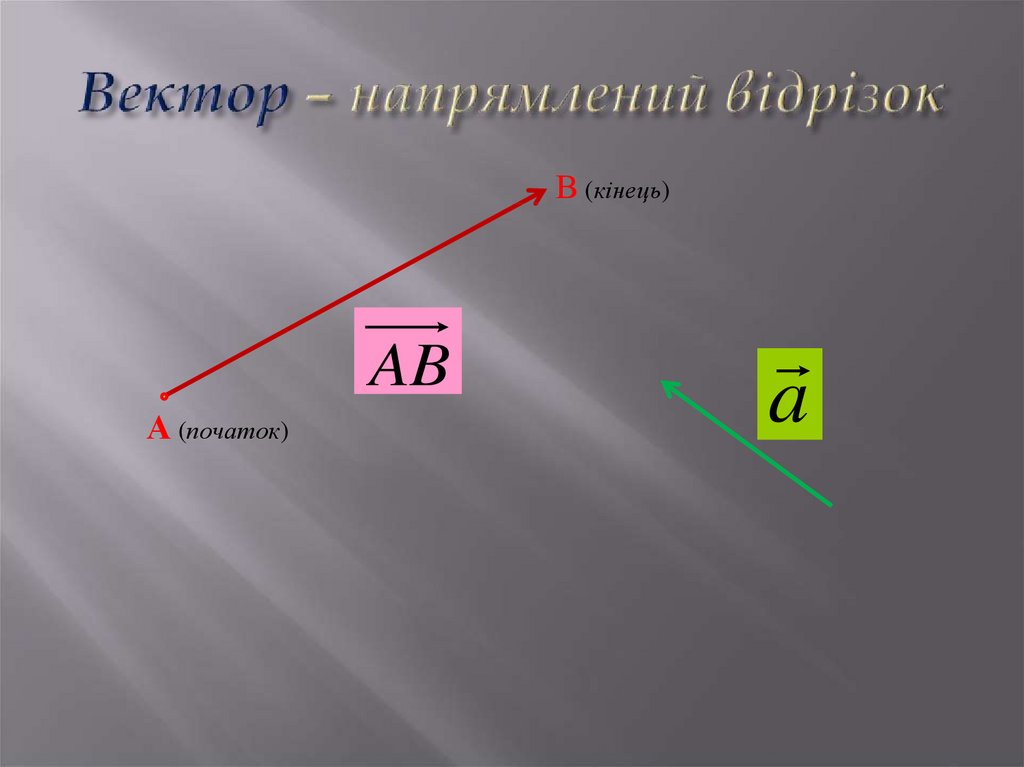
2. Вектор – напрямлений відрізок

В (кінець)
AB
А (початок)
a

3. Координати вектора

B x2 , y2 , z2
z
a (a1, a2 , a3 )
Щоб знайти координати
вектора потрібно від
відповідних координат
кінця вектора відняти
відповідні координати
початку
a1 x2 x1
a2 y2 y1
a3 z2 z1
A x1, y1, z1
o
x
y

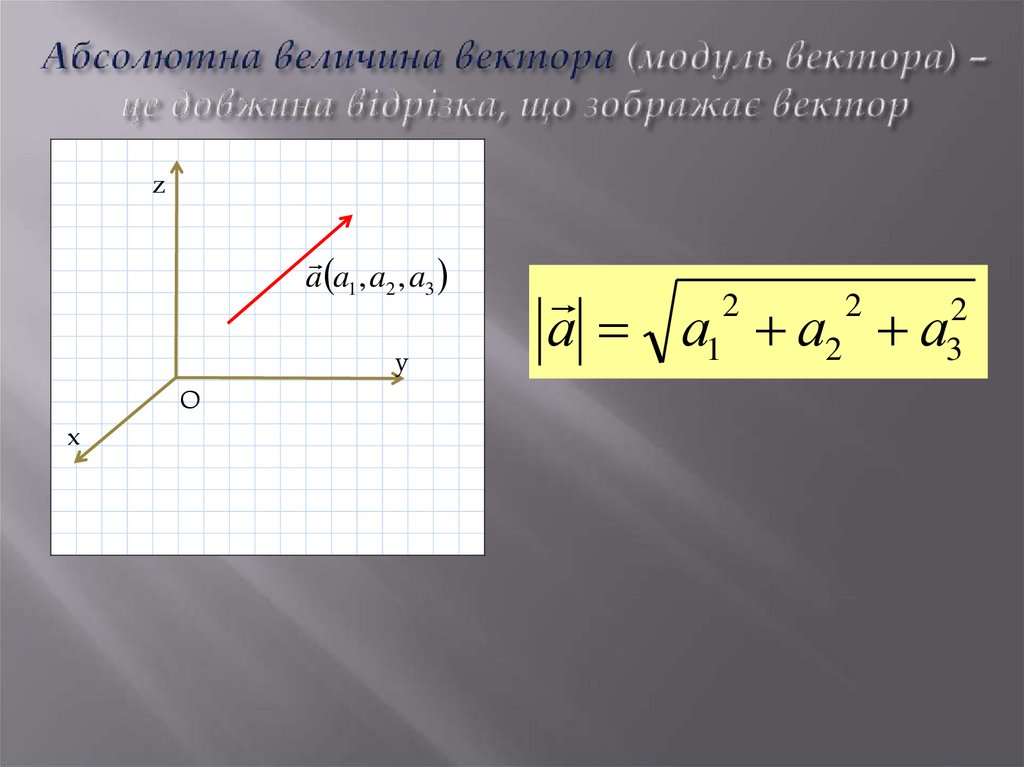
4. Абсолютна величина вектора (модуль вектора) – це довжина відрізка, що зображає вектор

z
a a1 , a2 , a3
y
O
x
2
2
2
а а1 а2 а3

5. Колінеарні вектори - це вектори, які лежать на паралельних прямих або належать одній прямій

Співнапрямлені
А
С
В
Д
AB CD
В
C
AB CD
a
a b
або
А
Протилежно напрямлені
D
a
b
або
a b
b

6. Рівні вектори

Два вектори називаються рівними, якщо вони
мають рівні модулі і однаково напрямлені.
a
b
| a | | b |
Якщо вектори задані координатами, то
a1 b1
а ( а1 , а2 , а3 ) b (b1 , b2 , b3 ) a2 b2
a b
3
3

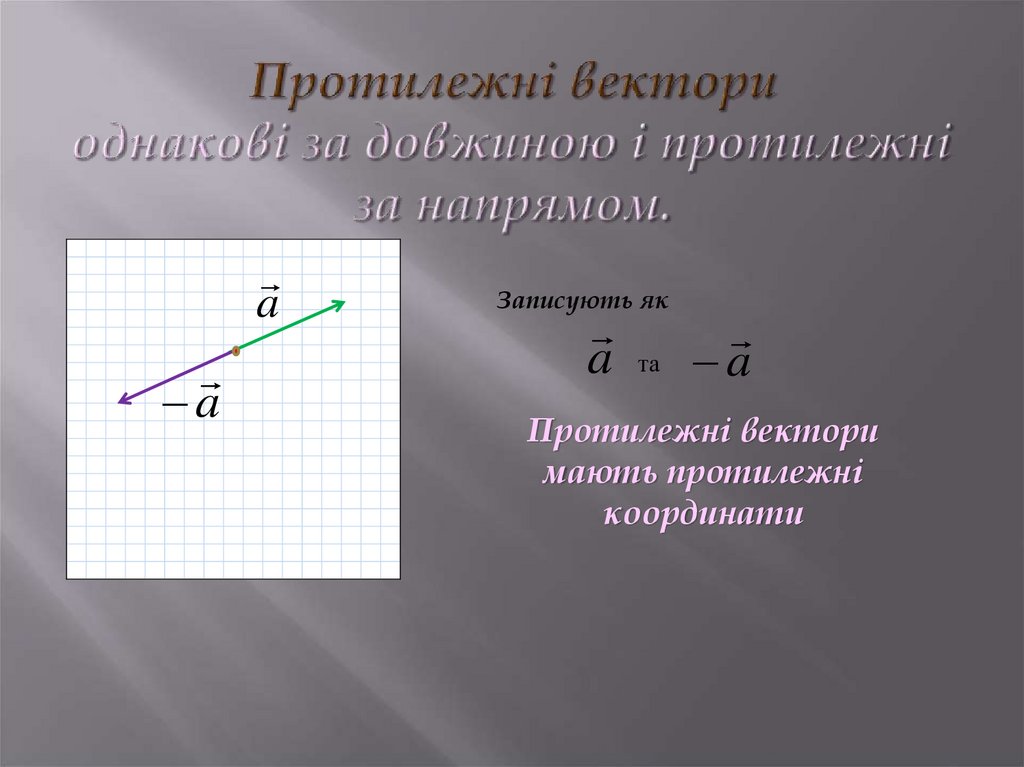
7. Протилежні вектори однакові за довжиною і протилежні за напрямом.

a
a
Записують як
a
та
a
Протилежні вектори
мають протилежні
координати

8. Види векторів

Одиничні вектори –
модулі яких
дорівнюють одиниці
a
a 1
Нульові вектори –
вектори, довжина яких
дорівнює нулю, не
мають напряму,
записують як
0

9. Види векторів

Координатні вектори, або орти, - одиничні вектори,
напрями яких збігаються з напрямами осей координат.
Орти паралельні напряму осей ОХ, ОУ, OZ
прямокутної системи координат, зазвичай їх
позначають як
z
e3
e1
х
o
e2
у
e1 , e2 , e3

10.

Домашнє завдання:
Підручник ст.198, § 20
№ 20.4, 20.7, 20.9, 20.11,
20.12, 20.14, 20.16, 20.30