Похожие презентации:
Позиционные и метрические задачи
1.
Позиционные иметрические
задачи
2.
Позиционные задачиВ позиционных задачах требуется
найти положение геометрических
фигур (точки, прямой, плоскости,
тела)удовлетворяющих условиям
задачи. Например, найти точку
пересечения прямой с плоскостью,
провести прямую или плоскость
через данную точку, найти линию
пересечения плоскостей и т.п.
3.
К позиционным задачамотносятся задачи на
взаимопринадлежность и
пересечение
4.
Основных позиционных задач напересечение две:
пересечение прямой с
плоскостью (1-я позиционная
задача);
пересечение двух плоскостей (2-я
позиционная задача)
5.
Алгоритм пересечения прямой сплоскостью
1.Заключить прямую в
проецирующую плоскость.
2.Построить линию пересечения
вспомогательной плоскости с
заданной.
3.Определить искомую точку на
пересечении полученной линии с
заданной прямой.
4.Определить видимость прямой.
6.
1. Пересечение прямой линииобщего положения с плоскостью
общего положения
7.
b'А (70, 30, 5)
В (30, 7, 45)
С (10, 40, 15)
c'
x
a'
b
a
c
8.
b'D (60, 40, 25)
E (15, 25, 5)
d'
c'
x
e'
a'
b
e
a
c
d
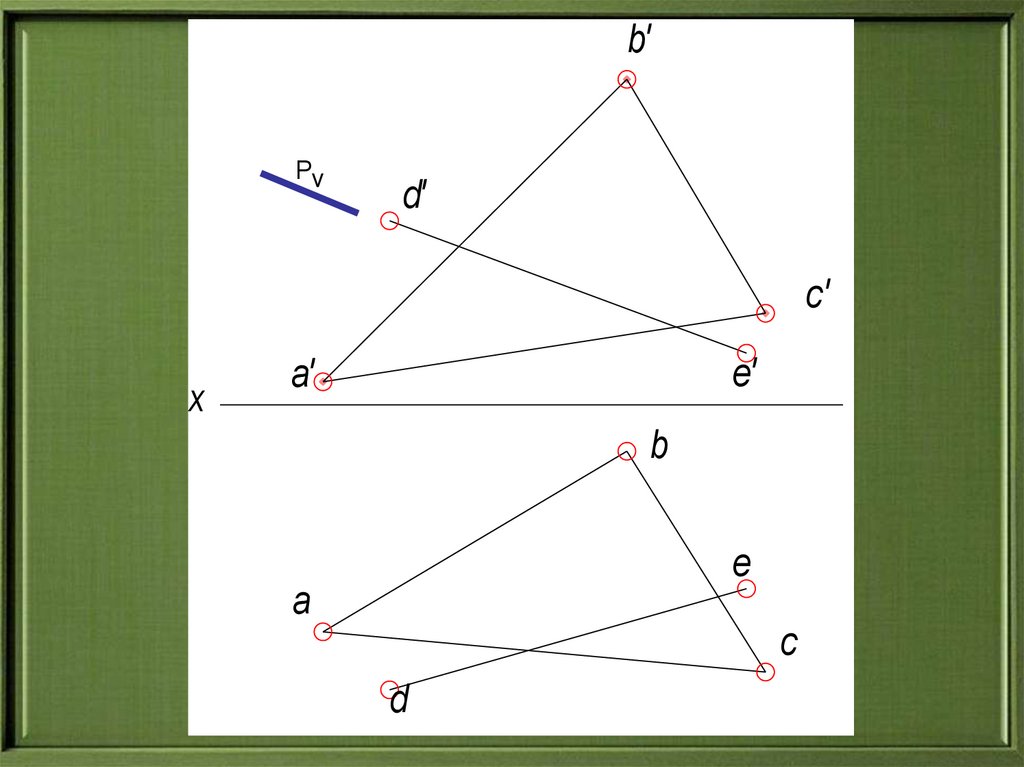
9.
b'Pv
d'
c'
x
e'
a'
b
e
a
c
d
10.
b'Pv
d' 2'
b'
Pv
x
a'
x
a'
e'
c'
e'
b
b
e
a
c'
1'
d'
a
e
c
c
d
d
11.
b'Pv
d' 2'
c'
1'
x
a'
e'
b
e
a
c
d
12.
b'Pv
d' 2'
c'
1'
x
a'
e'
b
e
a
c
d
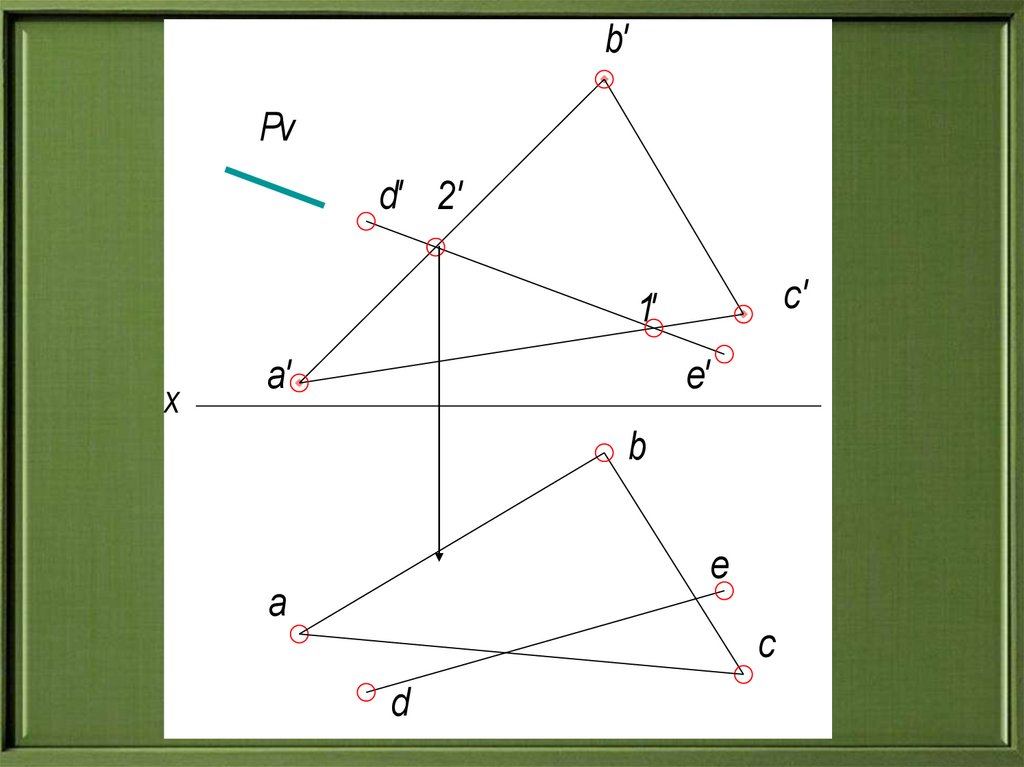
13.
b'Pv
d' 2'
c'
1'
x
a'
e'
b
2
e
a
c
d
14.
b'Pv
d' 2'
c'
1'
x
a'
e'
b
2
e
a
c
d
15.
b'Pv
d' 2'
c'
1'
x
a'
e'
b
2
e
a
c
d
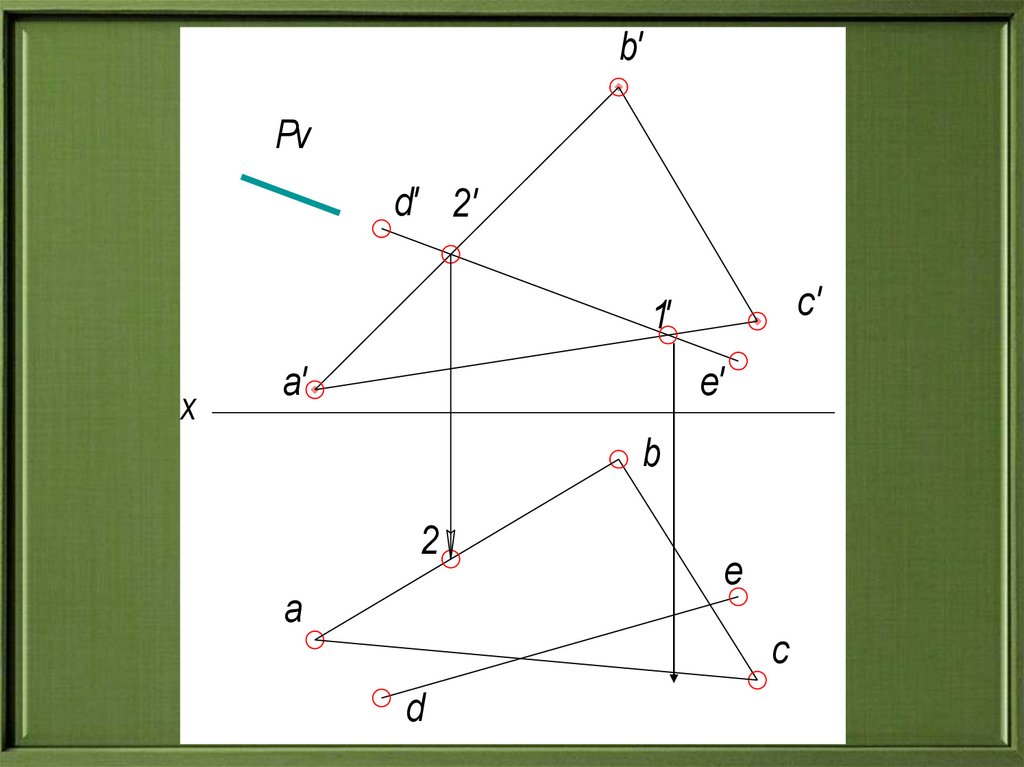
16.
b'Pv
d' 2'
c'
1'
x
a'
e'
b
2
e
a
c
d
1
17.
b'Pv
d' 2'
c'
1'
x
a'
e'
b
2
e
a
c
d
1
18.
b'Pv
d' 2'
c'
1'
x
e'
a'
b
2
e
a
m
c
d
1
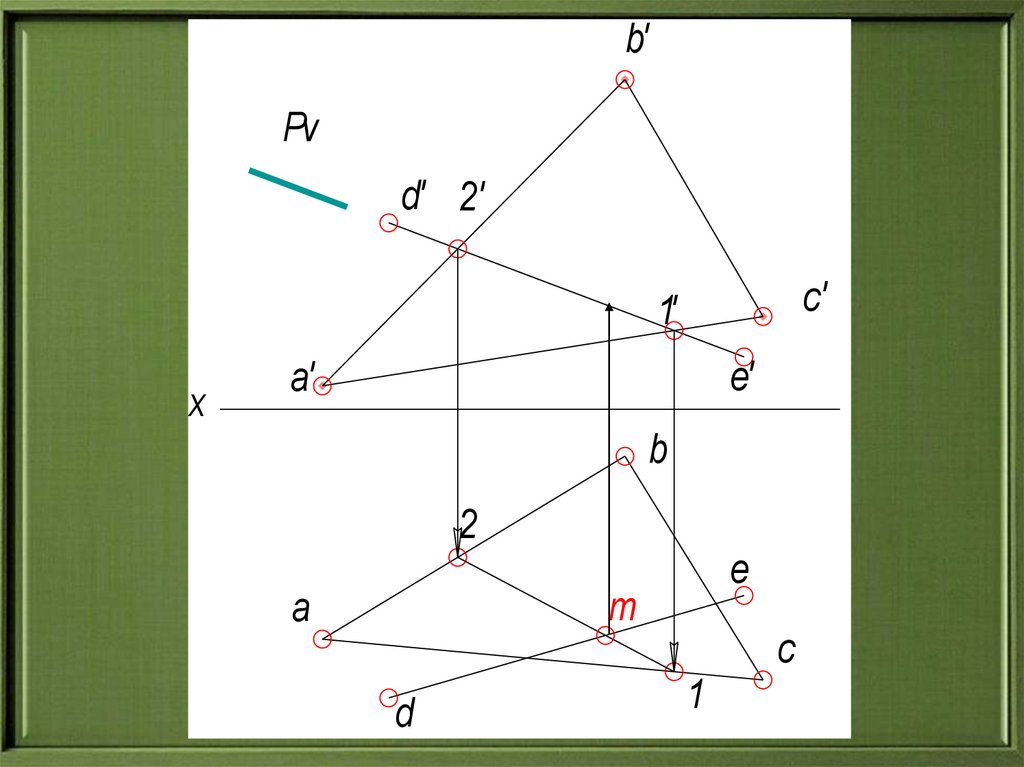
19.
b'Pv
d' 2'
c'
1'
x
e'
a'
b
2
e
m
a
c
d
1
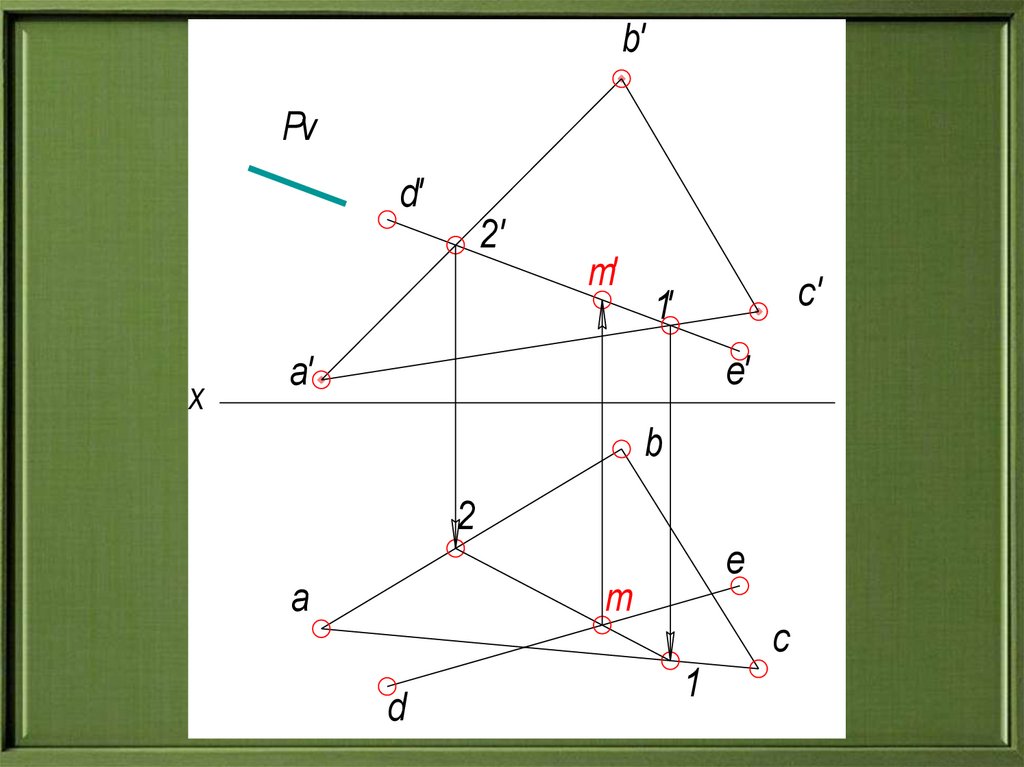
20.
b'Pv
d'
2'
m'
x
c'
1'
e'
a'
b
2
e
a
m
c
d
1
21.
b'Pv
d'
(2') 3'
x
m'
c'
1'
e'
a'
b
2
e
m
a
c
d
1
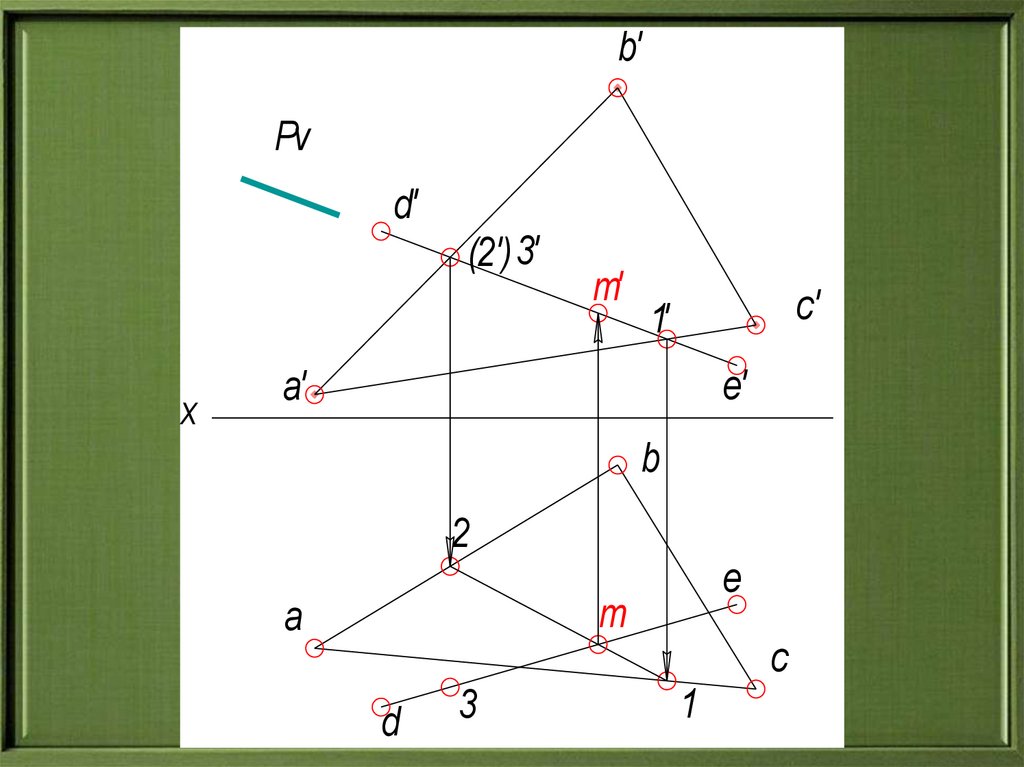
22.
b'Pv
d'
(2') 3'
x
m'
c'
1'
e'
a'
b
2
e
m
a
c
d
3
1
23.
b'Pv
d'
(2') 3'
m'
x
c'
1'
e'
a'
b
2
e
m
a
c
d
3
1
24.
b'Pv
d'
(2') 3'
x
m'
c'
1'
e'
a'
b
2
m
a
d
3
e
(4)5
c
1
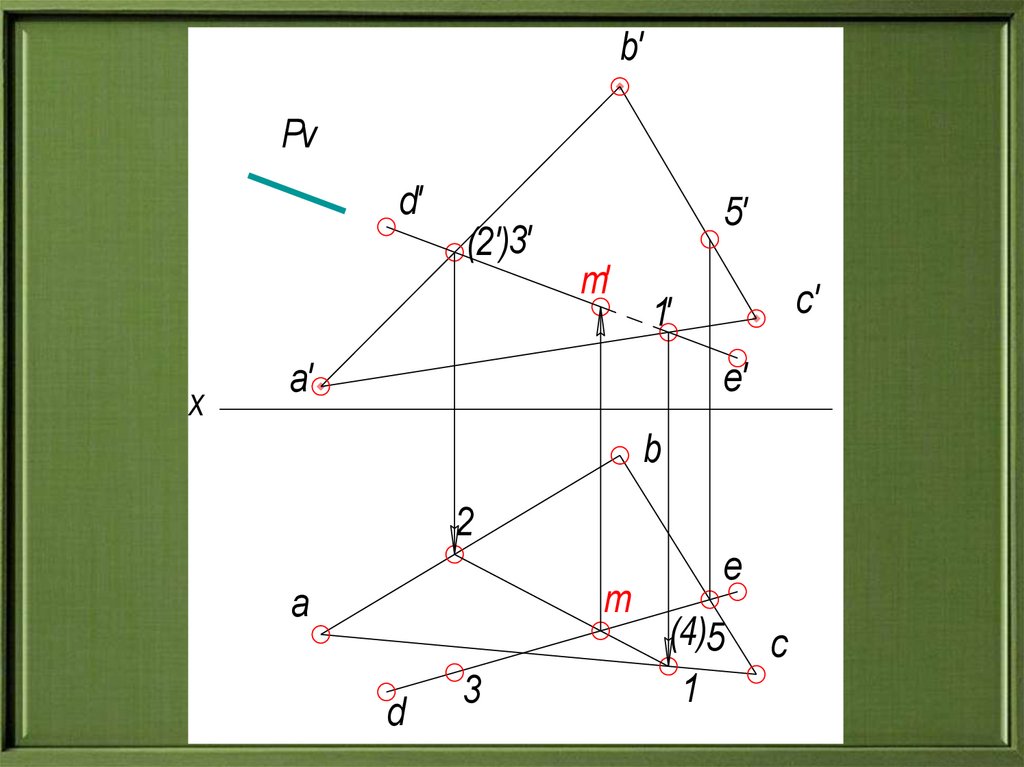
25.
b'Pv
d'
5'
(2')3'
m'
x
c'
1'
e'
a'
b
2
m
a
d
3
e
(4)5
1
c
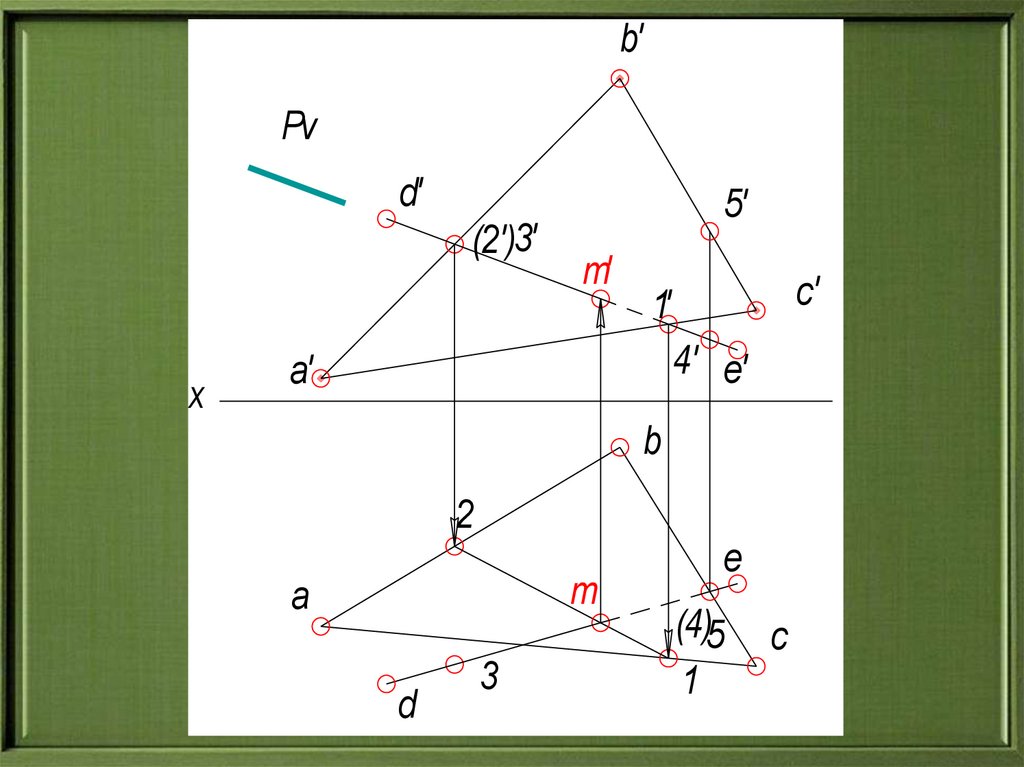
26.
b'Pv
d'
(2')3'
x
5'
m'
c'
1'
4' e'
a'
b
2
m
a
d
3
e
(4)5
1
c
27.
b'Pv
d'
(2')3'
x
5'
m'
c'
1'
4' e'
a'
b
2
m
a
d
3
e
(4)5
1
c
28.
b'Pv
d'
(2')3'
x
5'
m'
c'
1'
4' e'
a'
b
2
m
a
d
3
e
(4)5
1
c
29.
b'Pv
d'
(2')3'
x
5'
m'
c'
1'
4' e'
a'
b
2
m
a
d
3
e
(4)5
1
c
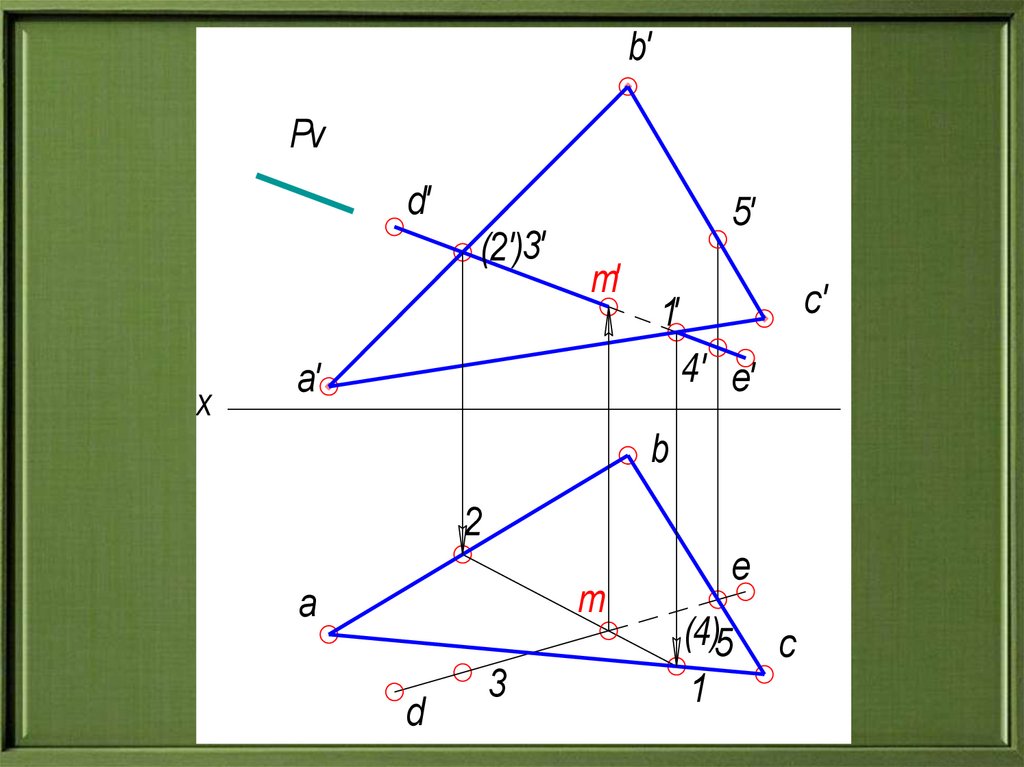
30.
b'Pv
d'
(2')3'
x
5'
m'
c'
1'
4' e'
a'
b
2
m
a
d
3
e
(4)5
1
c
31.
b'Pv
d'
(2')3'
x
5'
m'
c'
1'
4' e'
a'
b
2
m
a
d
3
e
(4)5
1
c
32.
2. Пересечение прямой линииобщего положения с
проецирующей плоскостью
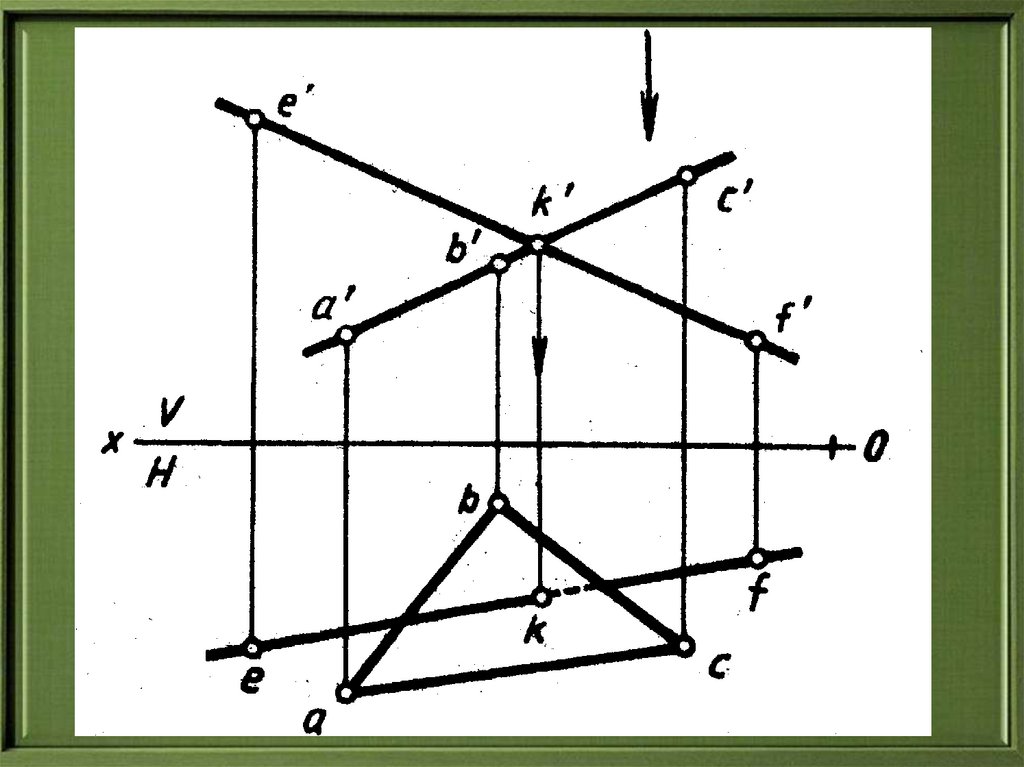
33.
Построение точки пересеченияпрямой с проецирующей
плоскостью сводится к построению
второй проекции точки на эпюре,
так как одна проекция точки всегда
лежит на следе проецирующей
плоскости, потому что все, что
находится в проецирующей
плоскости, проецируется на один из
следов плоскости
34.
35.
Домашнее задание1. Постройте проекции
точки пересечения
прямой MN c
плоскостью
четырехугольника
ABCD. Определите
видимость прямой
относительно
плоскости: А(45,5,32);
В(15,30,32); С(30,50,5);
D(65,25,5); M(75,40,32);
N(5,20,5)
X
o
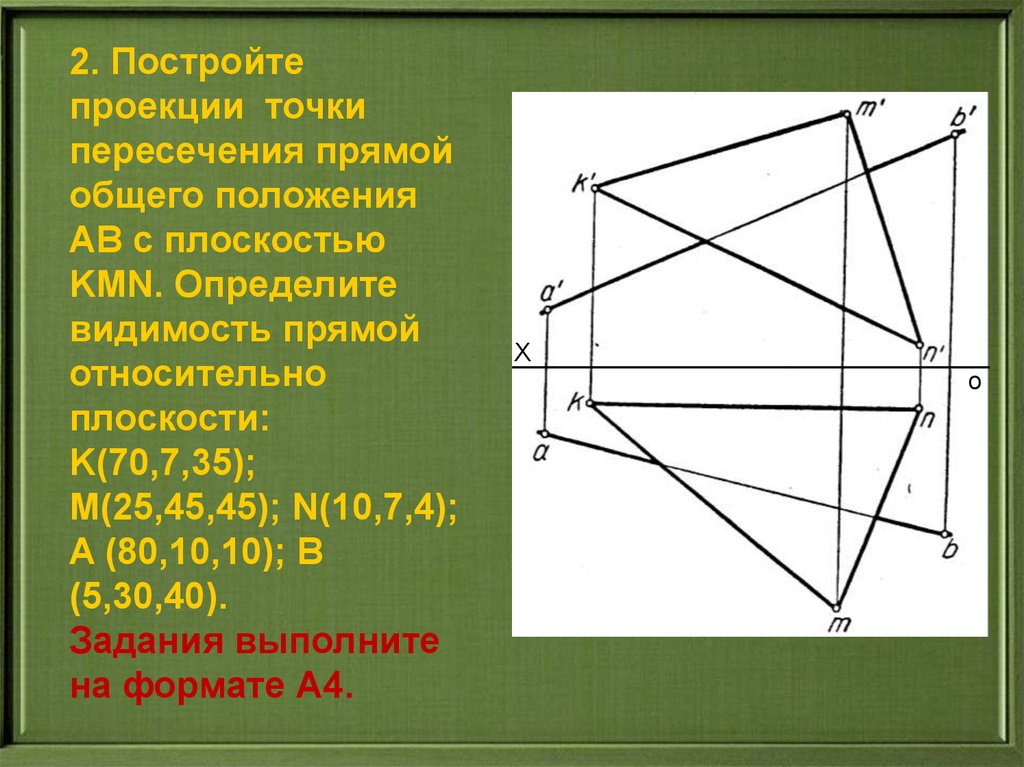
36.
2. Постройтепроекции точки
пересечения прямой
общего положения
АВ c плоскостью
KMN. Определите
видимость прямой
относительно
плоскости:
K(70,7,35);
M(25,45,45); N(10,7,4);
A (80,10,10); B
(5,30,40).
Задания выполните
на формате А4.
X
o
37.
Метрические задачиМетрическими называются задачи, в
которых необходимо определить
значения геометрических величин –
длин отрезков, размеры углов,
расстояние между геометрическими
фигурами, площади, объемы и т.п.
38.
Способыпреобразования
чертежа.
39.
Решение позиционных и метрическихзадач начертательной геометрии
значительно упрощается, если
геометрические фигуры находятся в
частном положении относительно
плоскостей проекций. Это может быть
достигнуто преобразованием
чертежа.
40.
Два основных способапреобразования чертежа:
1.Способ (или метод) перемены
плоскостей проекций(при
неподвижном объекте изменяют
положение плоскостей проекций).
2.Способ (или метод) вращения
(совмещения, плоскопараллельного
перемещения: при неподвижных
плоскостях проекций изменяют
положение объекта).
41.
Четыре основные задачи напреобразование:
1.Преобразовать прямую общего
положения в прямую уровня.
2.Преобразовать прямую общего
положения в проецирующую прямую.
3.Преобразовать плоскость общего
положения в проецирующую
плоскость.
4.Преобразовать плоскость общего
положения в плоскость уровня.
42.
Использование способовпреобразования для решения
позиционных и метрических
задач.
Способы преобразования
комплексного чертежа используются
для решения типовых задач на
определение расстояний и
натуральной величины углов и
плоских фигур, а именно:
43.
1) определение расстояния междуточками;
2) От точки до прямой;
3) От точки до плоскости;
4) Между параллельными прямыми,
между скрещивающимися прямыми;
5) Между параллельными плоскостями;
6) Определение натуральной величины
угла между прямой и плоскостями
проекций;
7) Угла наклона плоскости общего
положения к плоскостям проекций;
44.
8) Угла между пересекающимисяпрямыми общего положения;
9) Угла между прямой и плоскостью
общего положения;
10)Угла между плоскостями общего
положения;
11)Натуральной величины плоской
фигуры
45.
Способ перемены плоскостейпроекций
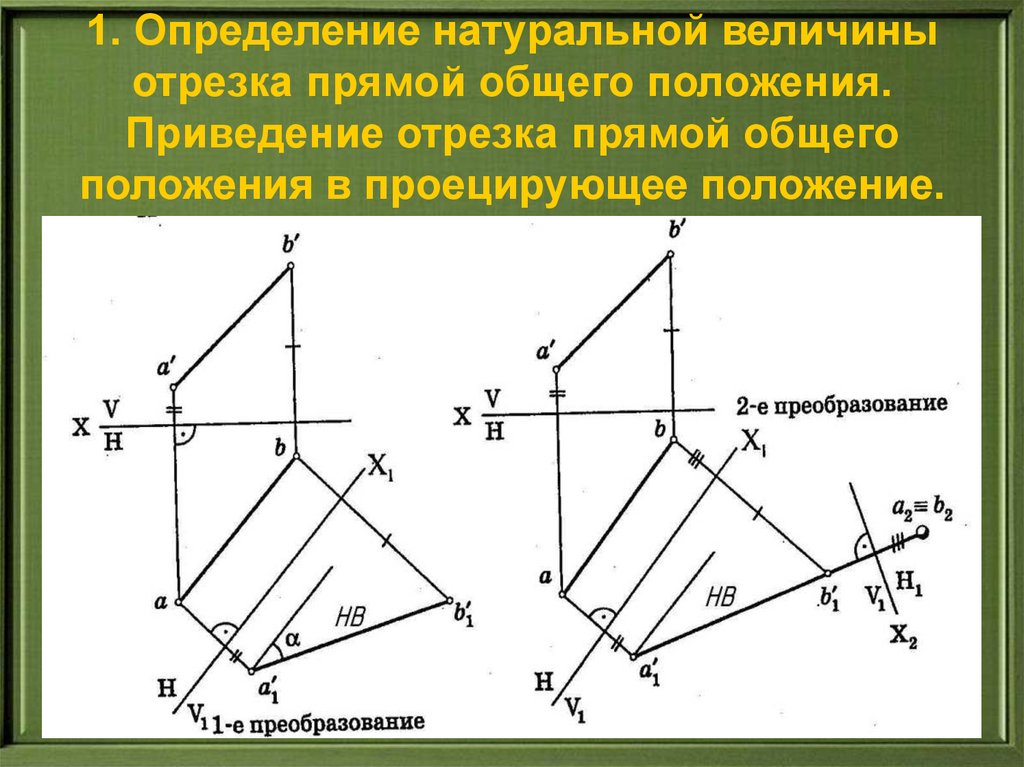
46.
1. Определение натуральной величиныотрезка прямой общего положения.
Приведение отрезка прямой общего
положения в проецирующее положение.
47.
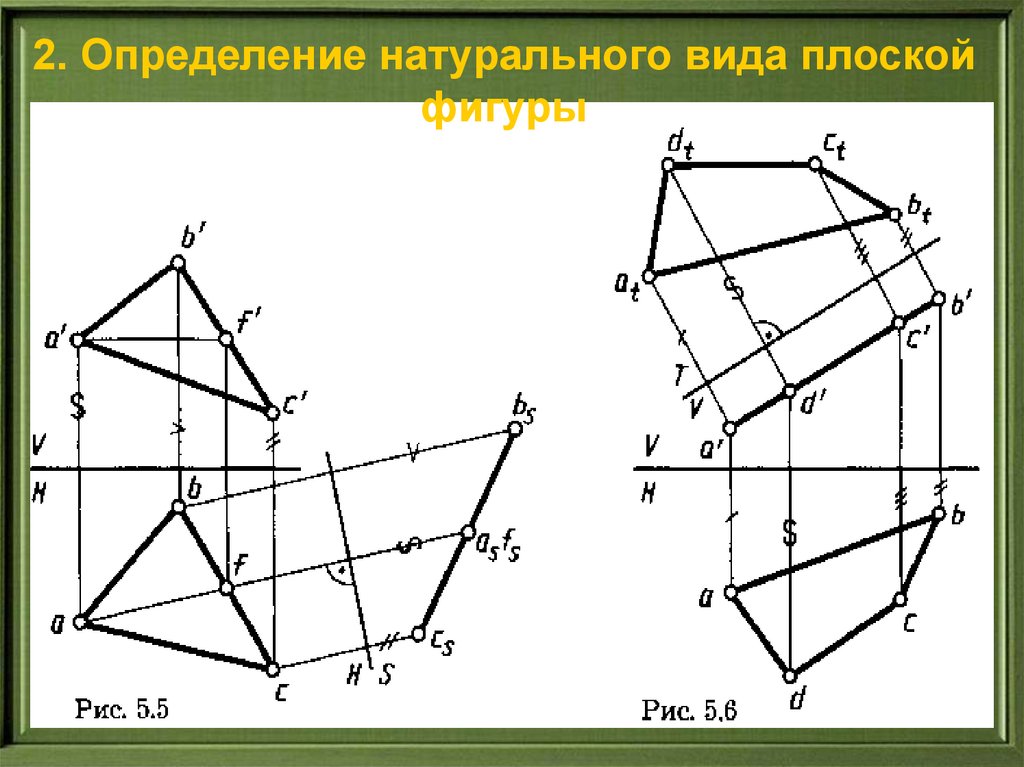
2. Определение натурального вида плоскойфигуры
48.
2. Определениенатурального
вида плоской
фигуры
49.
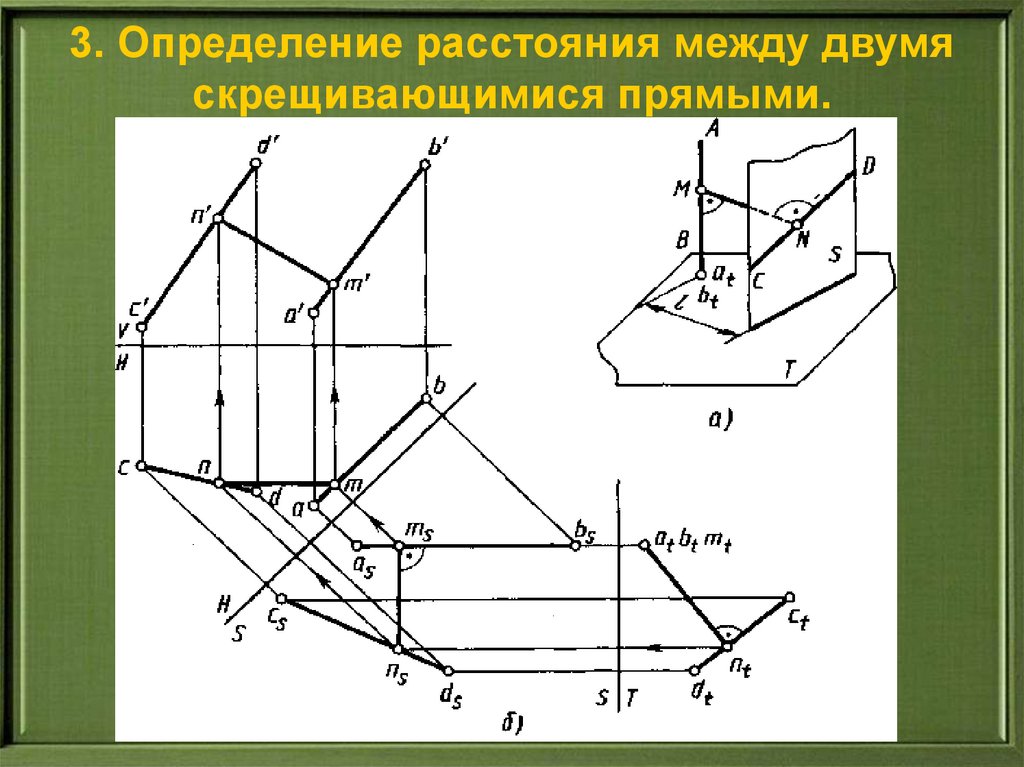
3. Определение расстояния между двумяскрещивающимися прямыми.



































 Инженерная графика
Инженерная графика








