Похожие презентации:
Позиционные задачи
1.
Позиционные задачи2.
При решениипозиционных задач
выясняют
взаимное
расположение (позицию)
двух и большего числа
геометрических фигур
Понятие взаимное
расположение включает
также принадлежность
одной фигуры другой
При этом возможны случаи:
1) полной
принадлежности:
– точка принадлежит
прямой;
– прямая принадлежит
плоскости;
2) пересечения:
– прямой с плоскостью,
поверхностью;
– двух плоскостей;
– плоскости с поверхностью;
– двух поверхностей;
3) отсутствие
принадлежности:
у двух скрещивающихся
прямых
3.
Пересечение плоскости общего положенияс проецирующей плоскостью
А2
L2
П2
A
B
K2
П2
В2
С2
x
C
x
A1
П1
А1
0
B1
C1
L1
K1
П1
П1
С1
П1 ( АВС)=KL
K1L1 ≡ 1
В1
4.
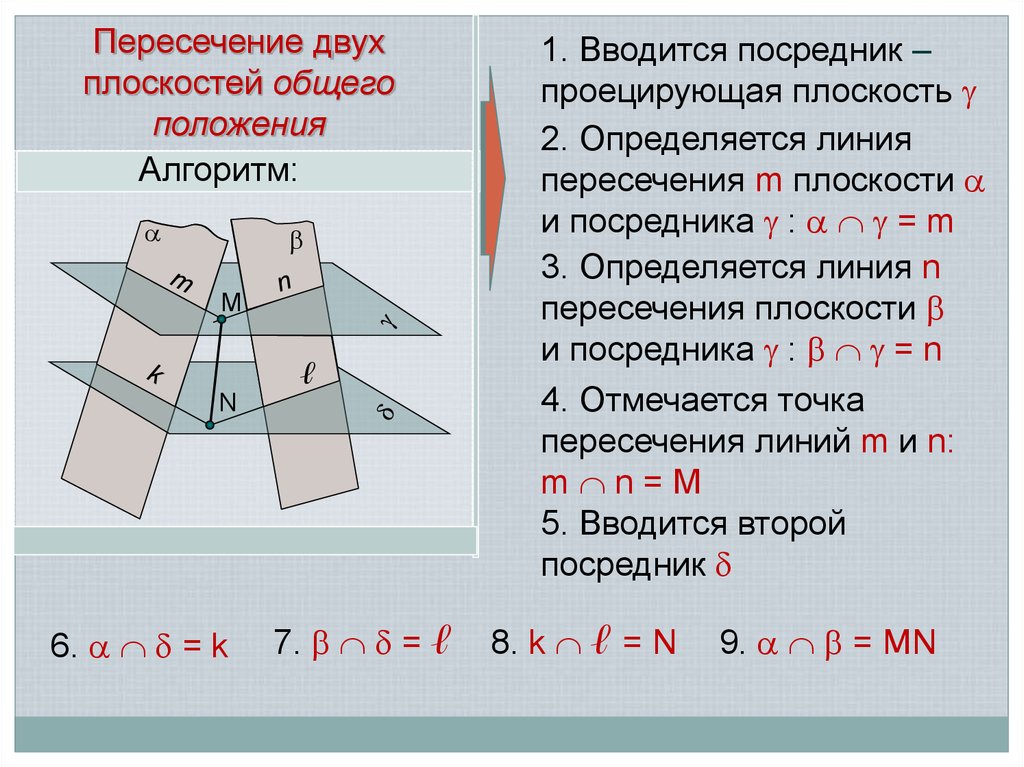
Пересечение двухплоскостей общего
положения
Алгоритм:
M
ℓ
N
6. = k
7. = ℓ
1. Вводится посредник –
проецирующая плоскость
2. Определяется линия
пересечения m плоскости
и посредника : = m
3. Определяется линия n
пересечения плоскости
и посредника : = n
4. Отмечается точка
пересечения линий m и n:
m n=M
5. Вводится второй
посредник
8. k ℓ = N
9. = MN
5.
ЗадачаПостроить линию пересечения
плоскостей и
12
2
I2
В2
22
62
M2
С2
52
А2
m2 ℓ 2
N2
32
42
(AB BC)
(m ll ℓ)
82
72
11 В1
А1
51
21
N1 31
71
61
С1 M1
m1
41
81
ℓ1
П2 a = 12; П2 a = 34;
12 34 = N;
IП2 a = 56; IП2 = 78;
56 78 = M;
а = MN
6.
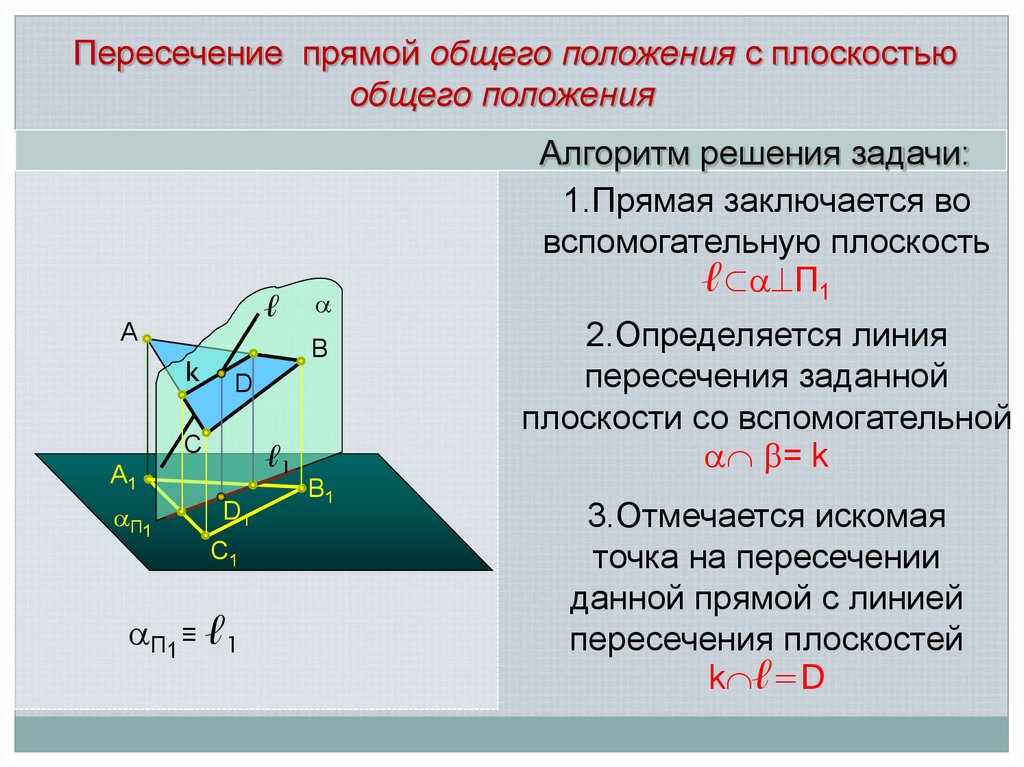
Пересечение прямой общего положения с плоскостьюобщего положения
ℓ
A
k
B
D
C
ℓ1
A1
П1
D1
C1
П1 ≡ ℓ1
B1
Алгоритм решения задачи:
1.Прямая заключается во
вспомогательную плоскость
ℓ⊂ П1
2.Определяется линия
пересечения заданной
плоскости со вспомогательной
= k
3.Отмечается искомая
точка на пересечении
данной прямой с линией
пересечения плоскостей
k ℓ=D
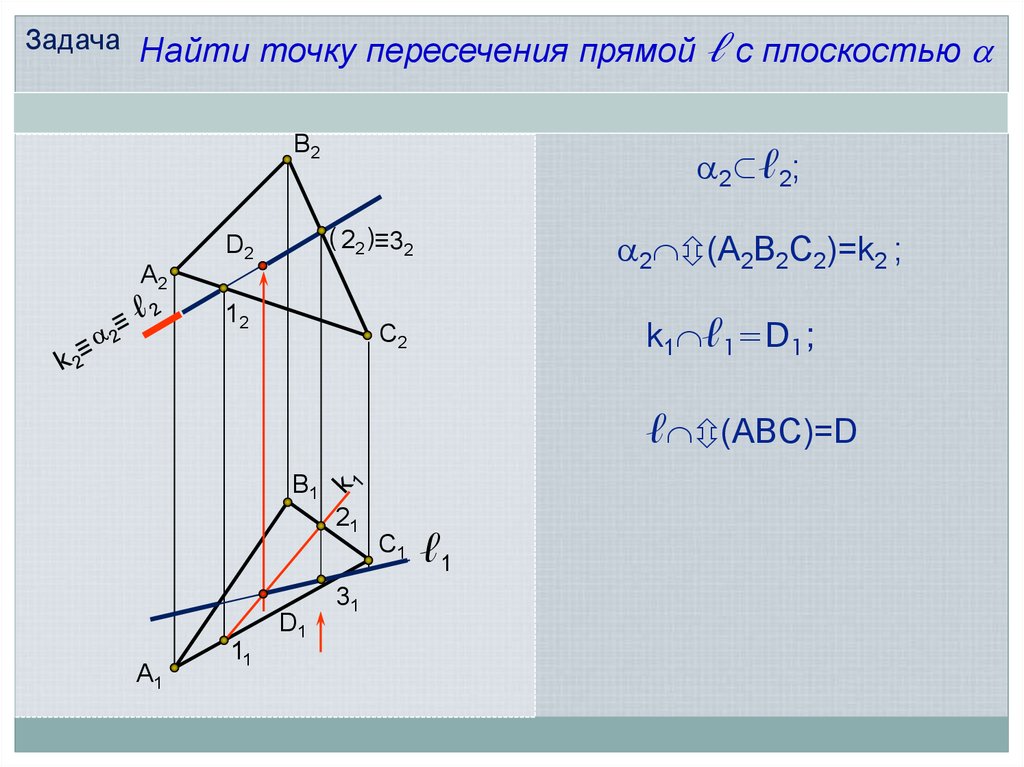
7.
Задача Найти точку пересечения прямойВ2
А2
2⊂ℓ2;
2 (А2В2С2)=k2 ;
( 22 )≡32
D2
ℓ с плоскостью
12
k1 ℓ1=D1;
С2
ℓ (ABC)=D
В1
21
А1
11
D1
31
С1
ℓ1
8.
Пересечение проецирующей прямой с плоскостью общегоположения
ℓ2
32≡ (42 )
12
В2
ℓ П1
ℓ ( АВС)=D
D2
А2
22
С2
В1
41
11
А1
ℓ1≡D1≡31
21
С1
9.
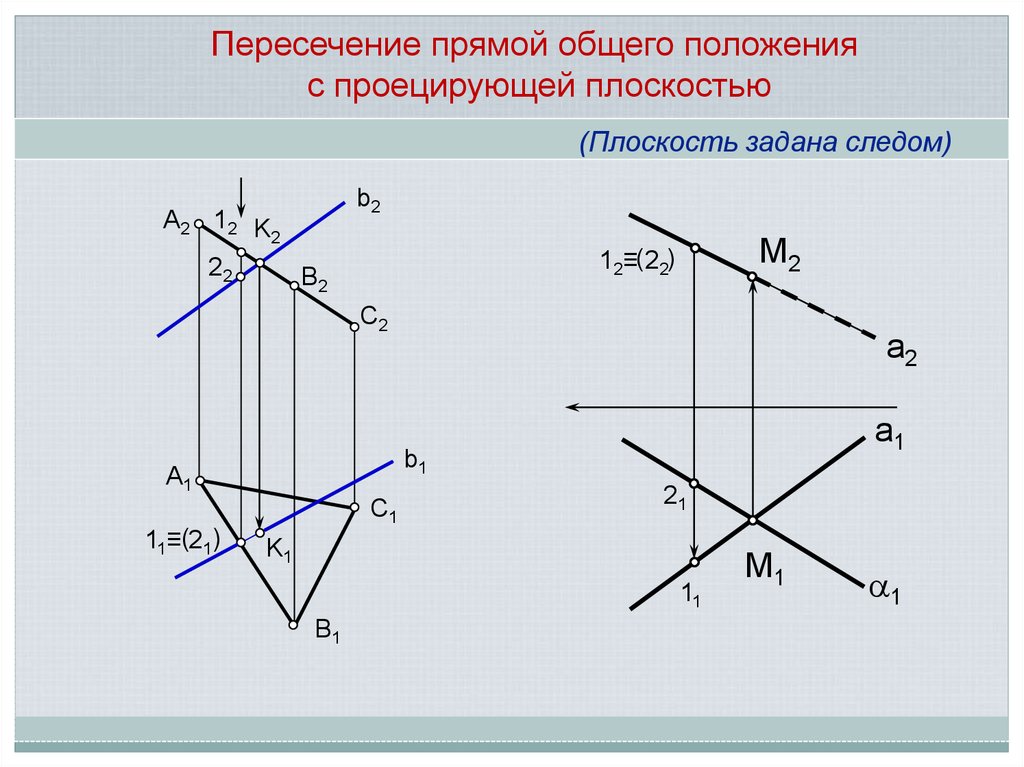
Пересечение прямой общего положенияс проецирующей плоскостью
(Плоскость задана следом)
A2 12 K
2
22
B2
b2
M2
12≡(22)
C2
a1
b1
A1
11≡(21)
a2
C1
21
K1
11
B1
M1
1





 Инженерная графика
Инженерная графика








