Похожие презентации:
Системы счисления
1.
Системы счисления2.
Система счисленияЭто совокупность правил записи чисел
посредством конечного набора символов
(цифр)
Непозиционные
Позиционные - значение цифры зависит от
позиции этой цифры в числе
3.
Позиционная система счисленияОснование системы счисления —количество
различных цифр, используемых в этой системе.
Вес разряда — отношение количественного
значения цифры в этом разряде к
количественному значению той же цифры в
нулевом разряде
pi = si
где
i — номер разряда
s — основание системы счисления.
4.
Разряды числа нумеруются справа налево,причем младший разряд целой части
(стоящий перед разделителем — запятой или
точкой) имеет номер ноль. Разряды дробной
части имеют отрицательные номера
число
5 4 82 , 5 2
Номера разрядов 3 2 1 0
-1 -2
5.
Представление чисел впозиционной системе счисления
Ask+…+As3+As2+As1+As0
где
A – цифры используемые в системе счисления
(количество символов = основанию системы счисления)
S - основание системы счисления
K – количество разрядов в числе
6.
ПримерЧисло 3754(10)
Количество разрядов 4
Основание системы счисления 10
Цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
3*103+7*102+5*101+4*100
3*1000 + 7*100 + 5*10 + 4*1
Числовое значение 3754
7.
ПримерЧисло 2432(5)
Количество разрядов 4
Основание системы счисления 5
Цифры (0, 1, 2, 3, 4)
2*53+4*52+3*51+2*50
2*125 + 4*25 + 3*5 + 2*1
250 +100+15+2
Числовое значение 367(10)
8.
Перевод в 10 систему счисленияпронумеровать разряды исходного числа
записать сумму, слагаемые которой
получаются как произведения очередной
цифры на основание системы счисления,
возведенное в степень, равную номеру
разряда
выполнить вычисления и записать
полученный результат (указав основание
новой системы счисления — 10).
9.
Перевод из девятиричной в 10314(9)
… As3+As2+As1+As0
3*92+1*91+4*90
3*81+1*9+4*1
243+9+4
256(10)
10.
2432(5)=2*53+4*52+3*51+2*50=367(10)367(10) = (((2*5+4)*5+3)*5+2)*1=2432(5)
367(10) = ((2*5+4)*5+3)*5+2=2432(5)
((2*5+4)*5+3)*5+2 → 2
(2*5+4)*5+3 → 3
(2*5)+4 → 4
11.
Перевод из 10 системыВыполнить последовательное деление с
остатком исходного числа и каждого
полученного частного на основание новой
системы счисления.
Записать вычисленные остатки, начиная с
последнего (т.е. в обратном порядке)
12.
Перевод 10 в девятиричную256(10)
256/9 = 28 остаток 4
28/9 = 3 остаток 1
3/9 = 0 остаток 3
Выписываем остатки
314 (9)
13.
Особенности перевода из 2 в 1010111(2)=1*24+0*23+1*22+1*21+1*20=27(10)
10111(2)=1*16+0*8+1*4+1*2+1*1=27(10)
10111(2)=1*16+1*4+1*2+1*1=27(10)
10111(2)=16+4+2+1=27(10)
14.
Быстрый способ перевода из 10 в 2 и из 2 в 10Перевод можно
выполнять через
сложение и вычитание
для этого воспользуемся
таблицей степеней
Степень числа 2
Значение
20
1
21
2
22
4
23
8
24
16
25
32
26
64
27
128
28
256
29
512
210
1024
15.
Переведем число 245(10) в двоичную системуВ таблице степеней 2 ищем первое максимальное число
которое можно вычесть из 245.
Это 128. Выполняем вычитание 245-128=117.
Находим следующее число которое можно вычесть из
полученного результата.
117-64=53
Продолжаем далее…
53-32=21
21-16=5
5-4=1
1-1=0
Вычисления заканчиваются когда в результате получаем 0
16.
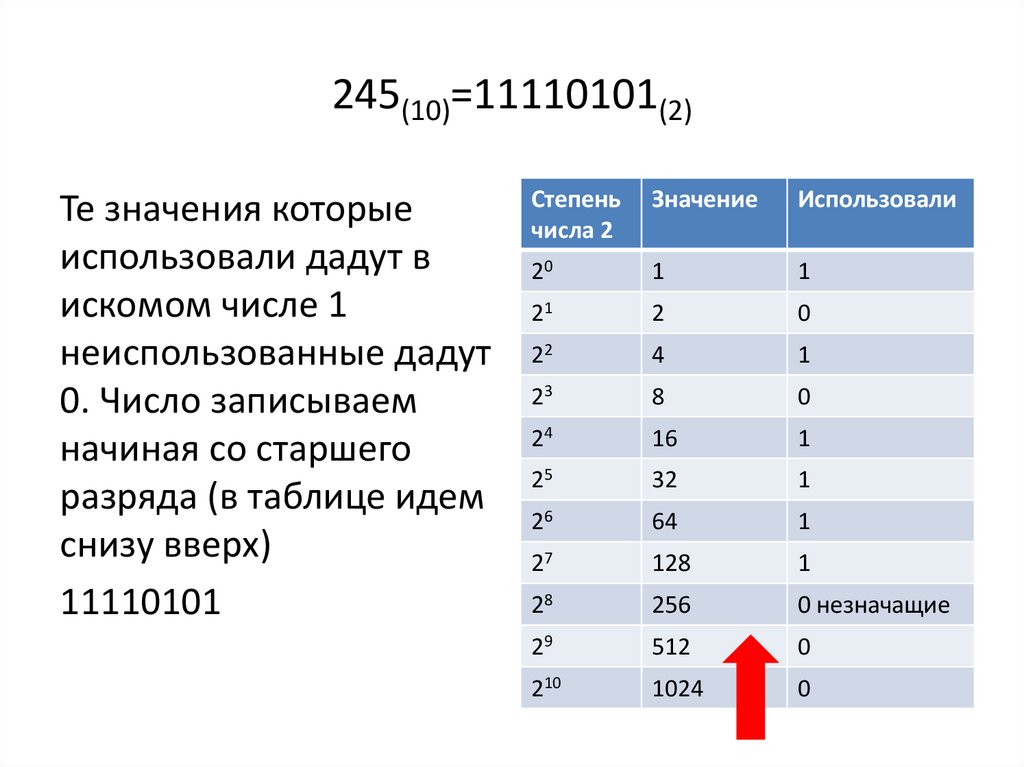
245(10)=11110101(2)Те значения которые
использовали дадут в
искомом числе 1
неиспользованные дадут
0. Число записываем
начиная со старшего
разряда (в таблице идем
снизу вверх)
11110101
Степень
числа 2
Значение
Использовали
20
1
1
21
2
0
22
4
1
23
8
0
24
16
1
25
32
1
26
64
1
27
128
1
28
256
0 незначащие
29
512
0
210
1024
0
17.
Переведем число 1011010(2) в десятичнуюсистему
В таблице степеней 2 ищем значения разряда в
позиции двоичного числа у которого стоит
единица.
1 разряд – 2
3 разряд – 8
4 разряд – 16
6 разряд – 64
Суммируем все числа 64+16+8+2=90
1011010(2)=90(10)
18.
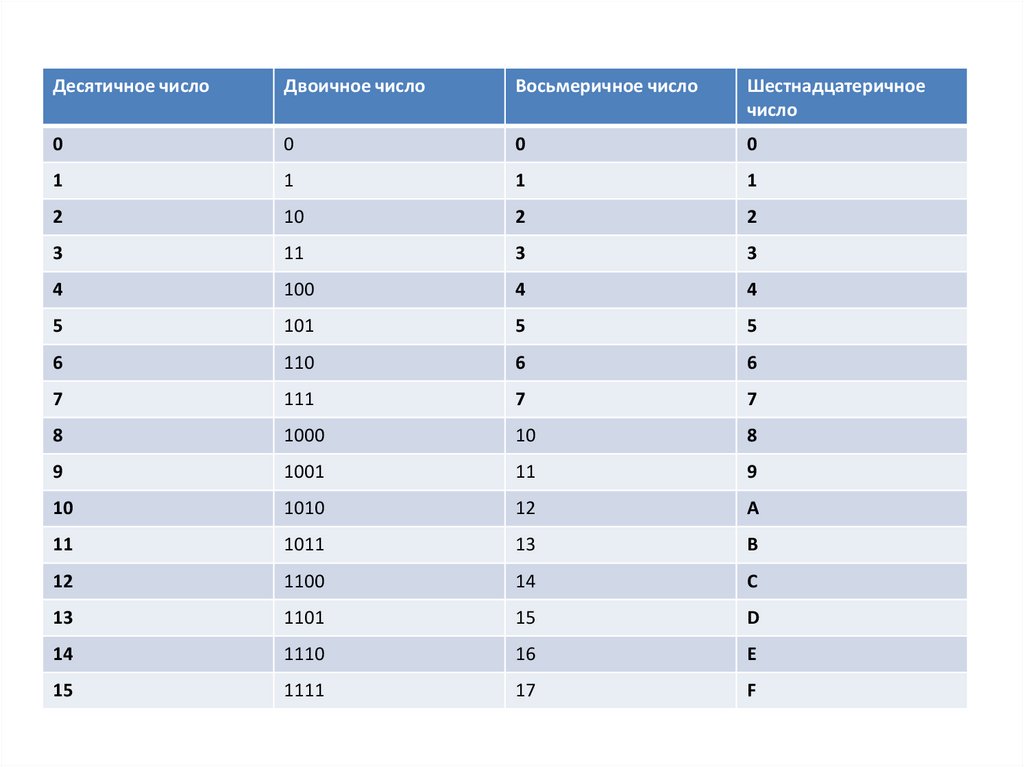
Десятичное числоДвоичное число
Восьмеричное число
Шестнадцатеричное
число
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
19.
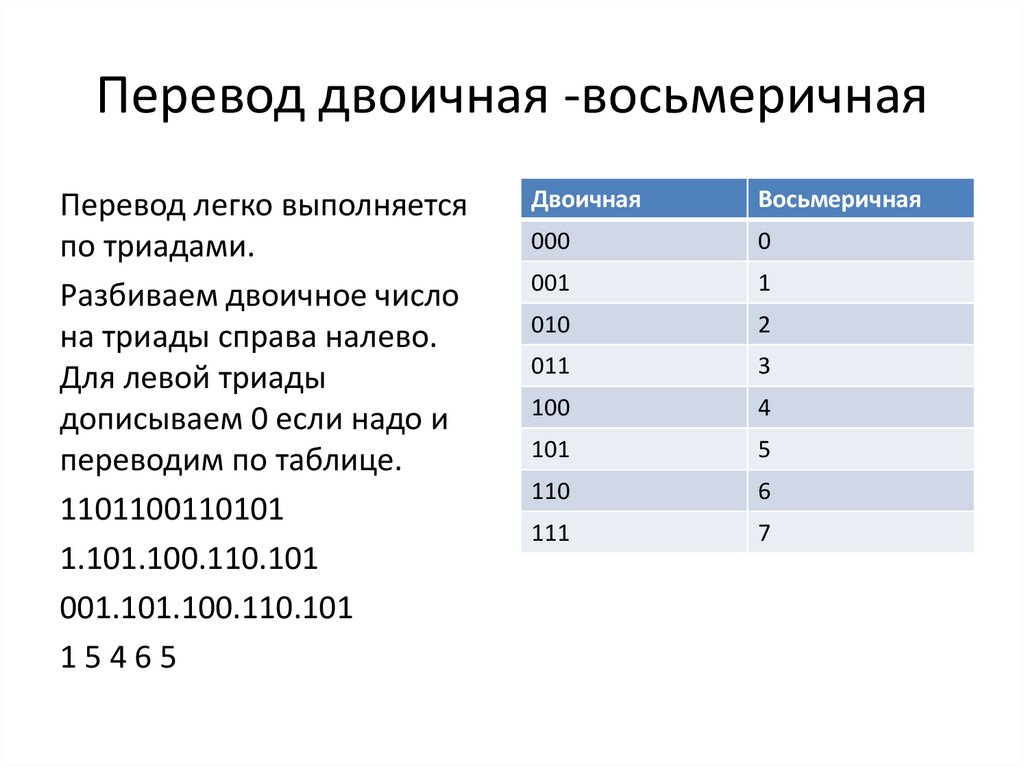
Перевод двоичная -восьмеричнаяПеревод легко выполняется
по триадами.
Разбиваем двоичное число
на триады справа налево.
Для левой триады
дописываем 0 если надо и
переводим по таблице.
1101100110101
1.101.100.110.101
001.101.100.110.101
15465
Двоичная
Восьмеричная
000
0
001
1
010
2
011
3
100
4
101
5
110
6
111
7
20.
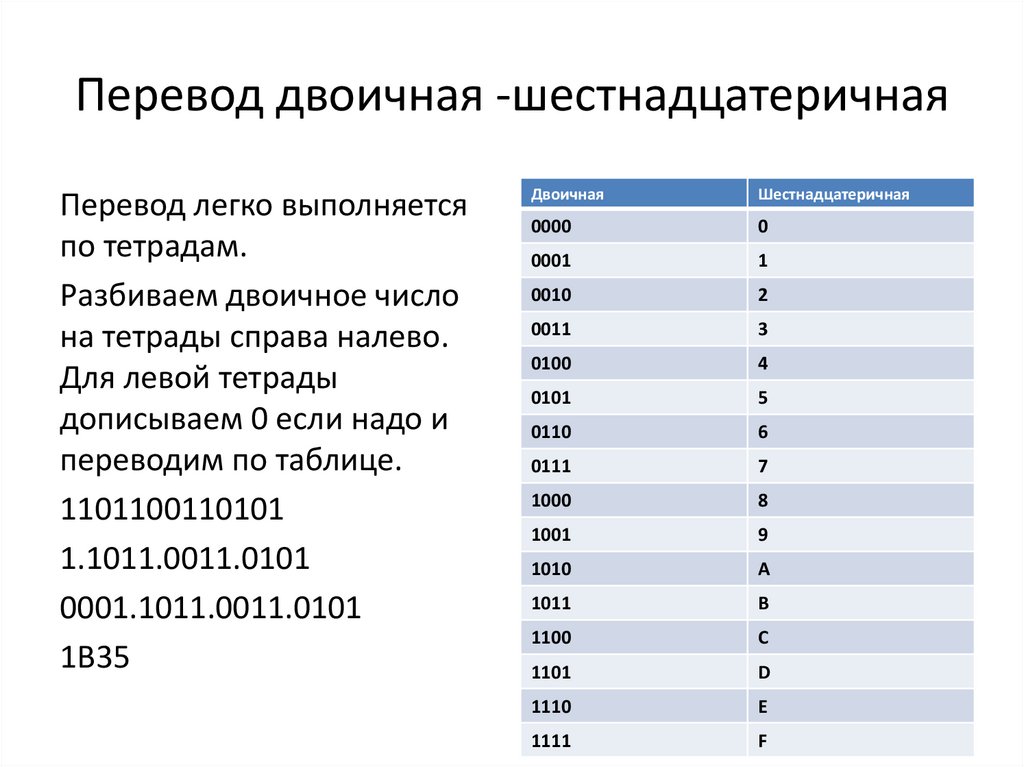
Перевод двоичная -шестнадцатеричнаяПеревод легко выполняется
по тетрадам.
Разбиваем двоичное число
на тетрады справа налево.
Для левой тетрады
дописываем 0 если надо и
переводим по таблице.
1101100110101
1.1011.0011.0101
0001.1011.0011.0101
1B35
Двоичная
Шестнадцатеричная
0000
0
0001
1
0010
2
0011
3
0100
4
0101
5
0110
6
0111
7
1000
8
1001
9
1010
A
1011
B
1100
C
1101
D
1110
E
1111
F
21.
Перевод из 10 в 8 и 16Перевод проще выполнять через двоичную
систему. 843(10)
Переводим в 2 вычитанием степеней двойки
843-512=331, 331-256=75, 75-64=11, 11-8=3, 3-2=1, 1-1=0
1101001011
Делим на триады 1 101 001 011 в восьмеричной 1513
Делим на тетрады 11 0100 1011 в шестнадцатеричной 34B
22.
Спасибо за внимание23.
Запись двоичных чисел можно воспроизвестипросто помня правила сложения в двоичной
системе
0+0=0
1+0=1
0+1=1
1+1=0 (1 переносим в старший разряд)
24.
Что надо знатьФормулу для представления числа в
позиционной системе счисления
Таблицы степеней (уметь рассчитывать, для
двоичных чисел помнить)
Запомнить запись чисел в двоичной системе
до числа 15 (или расчитать)
25.
Для остальных систем счисленияДля перевода из 10 в N систему выполняем
целочисленное деление и выписываем
остатки.
Для перевода из N в десятичную выполняем
умножение степени основания и сложение
полученных результатов









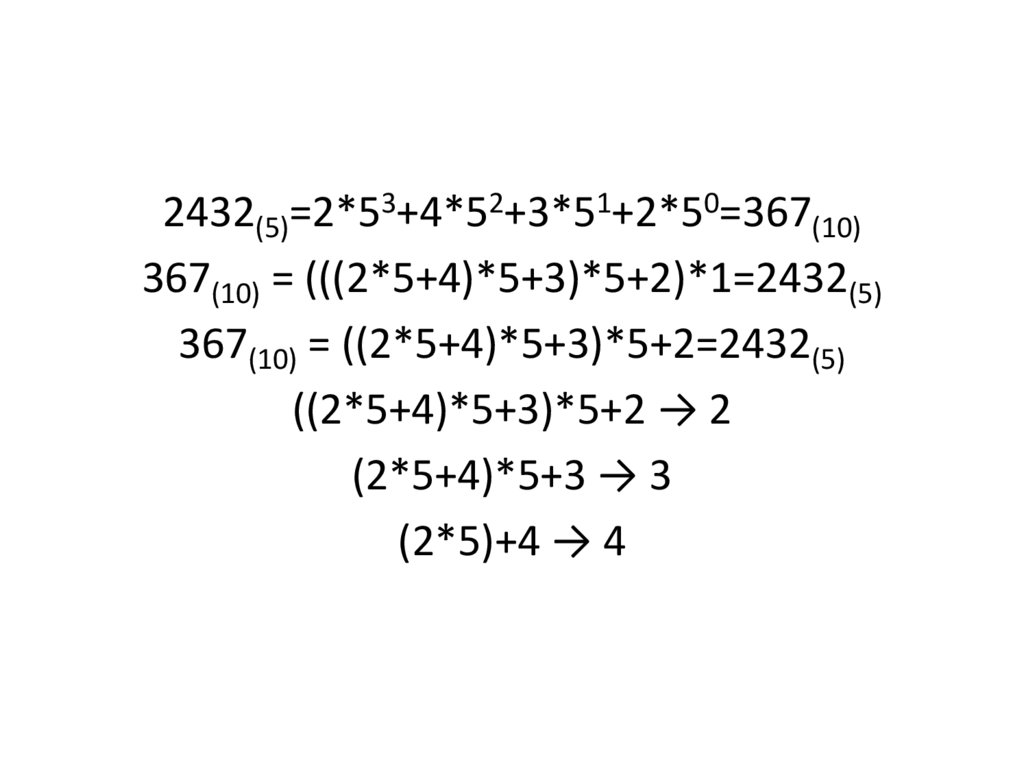











 Математика
Математика








