Похожие презентации:
Теоретическая механика
1.
Национальныйисследовательский
Томский политехнический
университет
Комплект слайд-лекций для технических
специальностей университета
2.
доктор физико-математических наук,профессор Отделения общетехнических дисциплин
Школы базовой инженерной подготовки
Томского политехнического университета
3.
Ускорение точки4. УСКОРЕНИЕ ТОЧКИ 1. Векторный способ
yO
M0
V0
x
5.
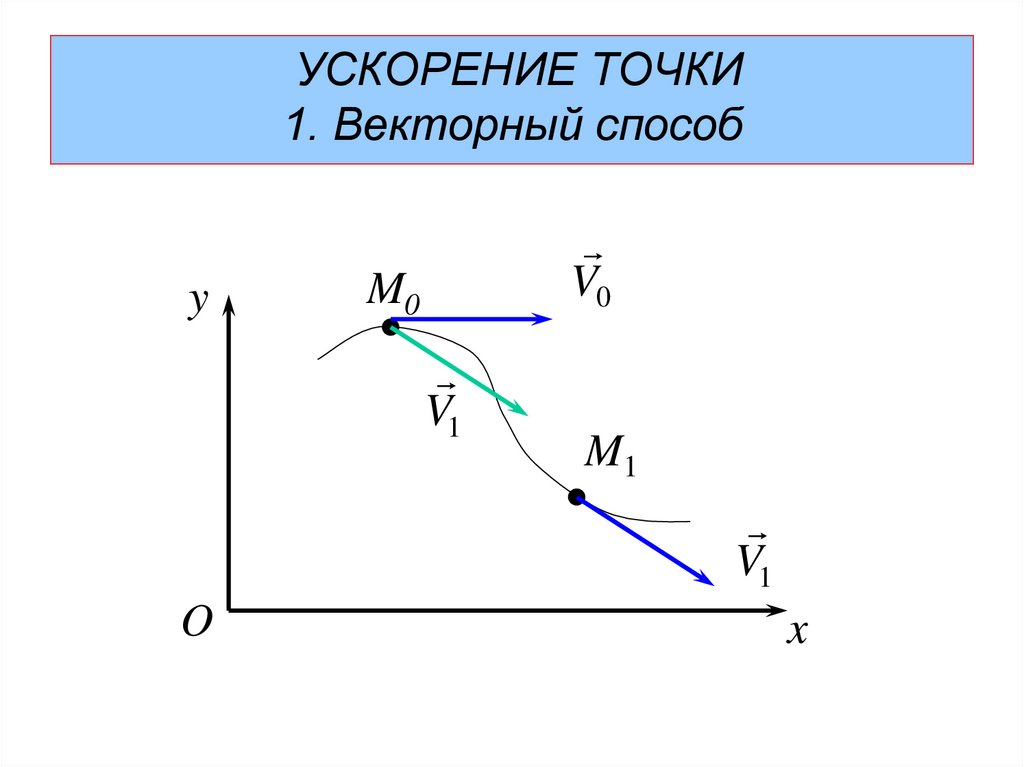
УСКОРЕНИЕ ТОЧКИ1. Векторный способ
y
M0
V0
M1
V1
O
x
6.
УСКОРЕНИЕ ТОЧКИ1. Векторный способ
y
V0
M0
V1
M1
V1
O
x
7.
УСКОРЕНИЕ ТОЧКИ1. Векторный способ
M0
y
ΔV
V0
M1
V1
O
x
8.
r r t - закон движения точкиV0 V t0 -скорость точки в положении М0
V1 V t0 t -скорость точки в положении М1
9.
r r t - закон движения точкиV0 V t0 -скорость точки в положении М0
V1 V t0 t -скорость точки в положении М1
V V1 V0 ; t t1 t0
aср
V
t
-среднее ускорение точки на отрезке
пути М0 М1
10.
VdV
a lim
t 0 t
dt
Мгновенное ускорение точки:
2
d r
dV
a
2
dt
dt
(1)
11. 2. Координатный способ
r xi yj zk2
2
2
d y
d z
d r d x
a 2 2 i 2 j 2 k
dt
dt
dt
dt
2
12.
2d x
dVx
;
a x 2 x
dt
dt
2
dVy
d y
;
a y 2 y
dt
dt
2
d z
dVz
.
a z 2 z
dt
dt
(2)
13.
Модуль вектора ускорения:a
2
ax
2
ay
2
az
Направление вектора ускорения:
ax
cos a , i ;
a
ay
cos a , j ;
a
az
cos a , k
a
(3)
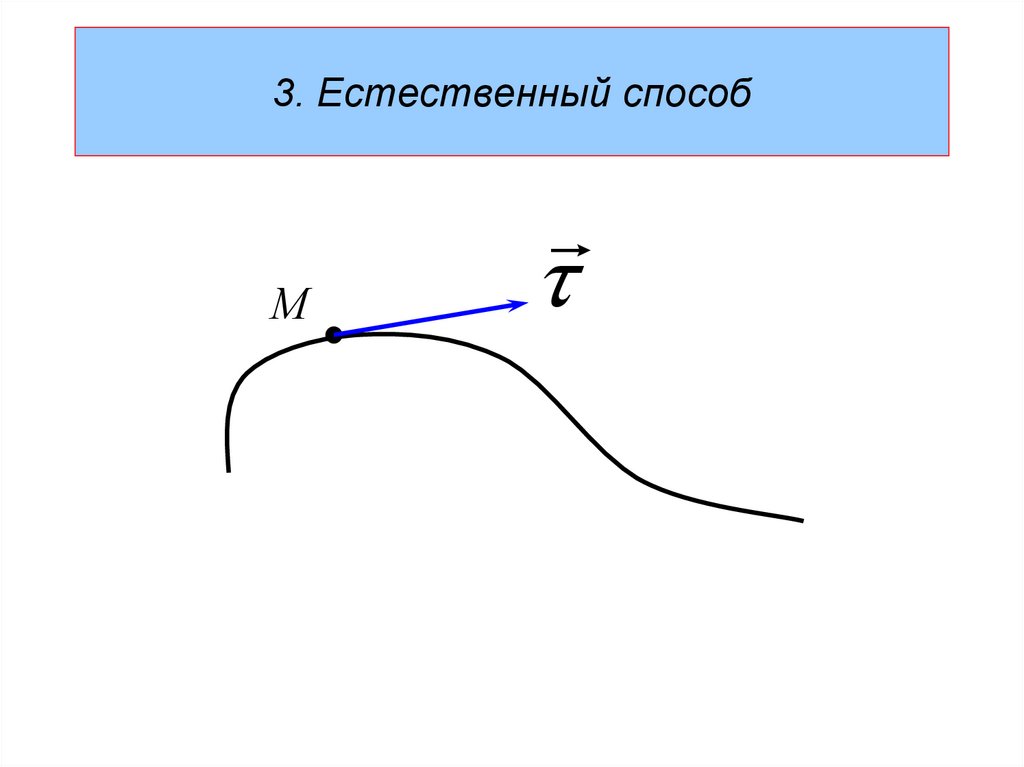
14. 3. Естественный способ
М15.
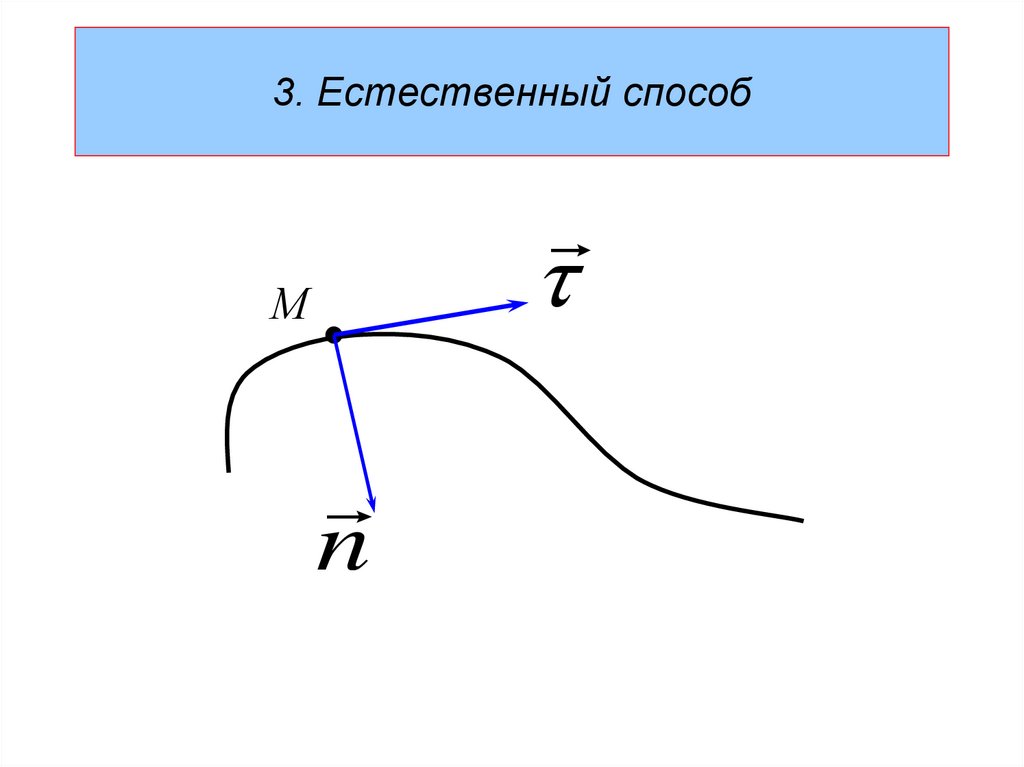
3. Естественный способМ
n
16.
3. Естественный способb
М
n
b n
17.
bНормальная плоскость
М
n
Спрямляющая плоскость
Соприкасающаяся плоскость
18.
Лекционная видеодемонстрация(дважды кликнуть по значку)
или выделить гиперссылку, кликнуть правой
кнопкой мыши, выбрать «Открыть
гиперссылку» и нажать левую кнопку мыши
Естественный трехгранник – YouTube
www.youtube.com/watch?v=GLs2ZtPqsVA
19.
М0V0
М1
M 0 M1 s
V1
- дуговая координата
- угол смежности
20.
dk
ds
1
ds
k
d
- кривизна кривой
- радиус кривизны в данной точке
21.
V Vd
dV dV
a
V
dt dt
dt
(4)
22.
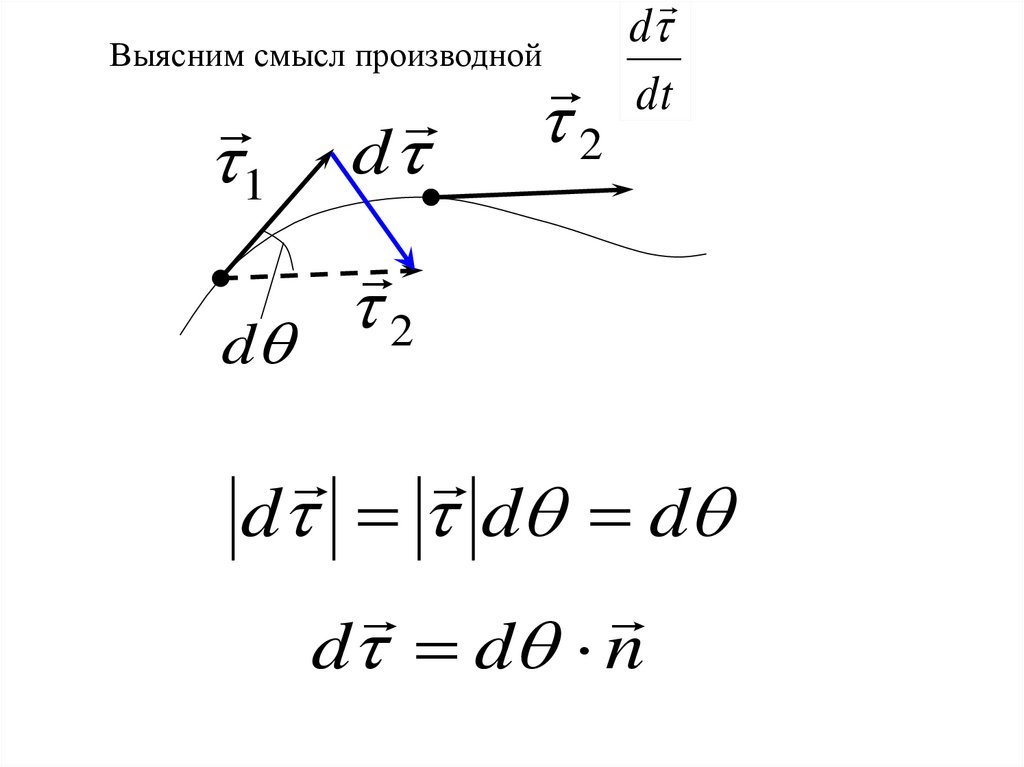
Выясним смысл производной1
2
d
dt
23.
Выясним смысл производной2
1
2
d
dt
24.
Выясним смысл производной1
d
2
d
2
d
dt
25.
Выясним смысл производнойd
1
2
d
dt
2
d
d d d
d d n
26.
Выясним смысл производнойd d
n
dt dt
d
dt
27.
d d d ds Vn
n n
dt dt
ds dt
28.
d d d ds Vn
n n
dt dt
ds dt
Формула (4) принимает вид:
2
dV V
a
n
dt
(5)
29.
Тангенциальное (касательное) ускорение:dV
a
dt
(6)
Нормальное ускорение:
an
V
2
(7)
Бинормальное ускорение:
ab 0
30.
aan
a
dV V
dt
2
a a
2
2
an
2
2
(8)
31. 4. Сложное движение точки. Теорема Кориолиса
Теорема о сложении скоростей:Vабс Vотн Vпер
(9)
32.
xM
x1
z1
O
y
z
y1
33.
xM
x1
r
z1
O
y
z
y1
- мгновенная угловая скорость подвижной системы
Ox1 y1z1 относительно неподвижной Ox yz
34.
dr -приращение радиус-вектора в системе Oxyz~ -приращение радиус-вектора в системе Ox y z
1 1 1
dr
35.
dr -приращение радиус-вектора в системе Oxyz~ -приращение радиус-вектора в системе Ox y z
1 1 1
dr
dr
-абсолютная производная
dt
~
dr
-локальная (относительная) производная
dt
36.
Vабсdr
dt
(10)
Vотн
~
dr
dt
(11)
Vпер r
(12)
37.
Vабс Vотн Vпер~
dr d r
r
dt
dt
(13)
38.
Vабс Vотн Vпер~
dr d r
r
dt
dt
Аналогично для любого вектора
~
dc d c
c
dt
dt
(13)
с:
(14)
39.
zz
y
О
x
О1
y
x
40.
Vот нz
М
аот н
z
y
О
x
О1
y
x
41.
Vот нz
М
аот н
z
О
x
Vпер
y
аО1
О1
y
x
42.
Vот нz
М
z
О
x
аот н
Vпер
y
аО1
О1
y
x
43. Теорема Кориолиса
aабс aотн апер акор(15)
44.
Теорема Кориолисаaабс aотн апер акор
~
~2
d Vот н d r
aот н
2
dt
dt
aпер a01 r r
aкор 2 Vотн
(15)
(16)
(17)
(18)
45.
Теорема КориолисаАбсолютное ускорение
точки при сложном
движении
складывается из
относительного,
переносного и
кориолисова
ускорений.
Гаспар-Гюстав Кориолис
(1792-1843)
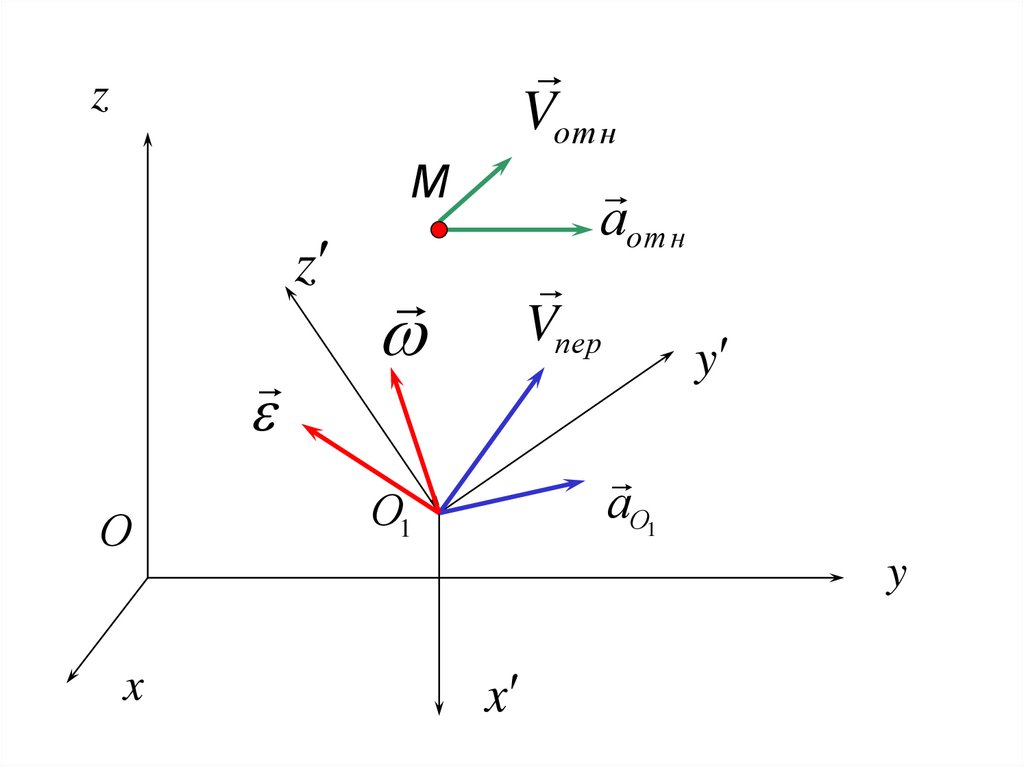
46.
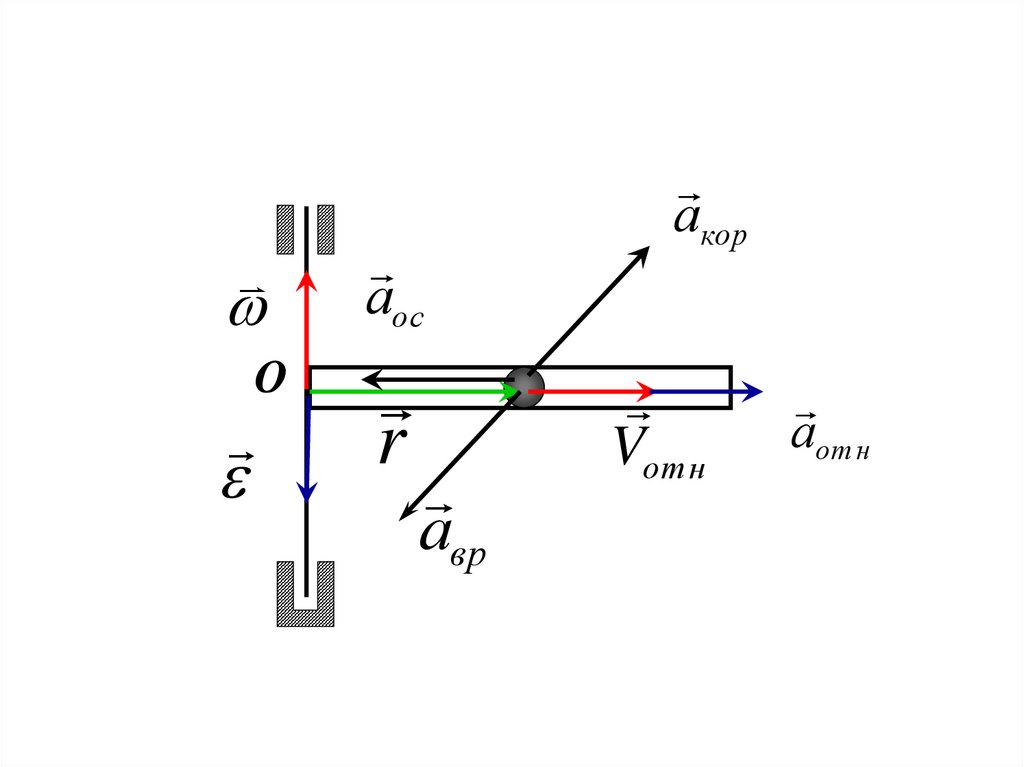
ПримерОпределить направления всех компонент ускорения
точки.
О
r
Vот н
аот н
47.
aпер a01 r rа01 0
aвр r
2
aос r r
(19)
(20)
48.
Оr
авр
Vот н
аот н
49.
аосО
r
авр
Vот н
аот н
50.
аосО
r
авр
акор
Vот н
аот н
51. Контрольные вопросы:
1. Возникает ли ускорение при равномерномдвижении точки по окружности?
2. Чем удобен естественный способ задания
движения?
3. Куда направлено ускорение Кориолиса в
случае вертикального падения точки в
северном полушарии?
52. ТЕСТОВЫЕ ЗАДАНИЯ
Для самоконтроля знаний рекомендуетсявыполнить тестовые задания из
Сборника коротких задач по теоретической
механике. Под ред. Кепе О.Э.
С. 104, 112, 114
53.
После просмотра и конспектирования слайдлекции необходимо прочитать указанныестраницы учебников и дополнить конспект
наиболее важными сведениями
1. Тарг С.М. Краткий курс теоретической механики:
Учеб. для втузов.- 10-е изд. – М: ВШ, 1986. С.
100-103.










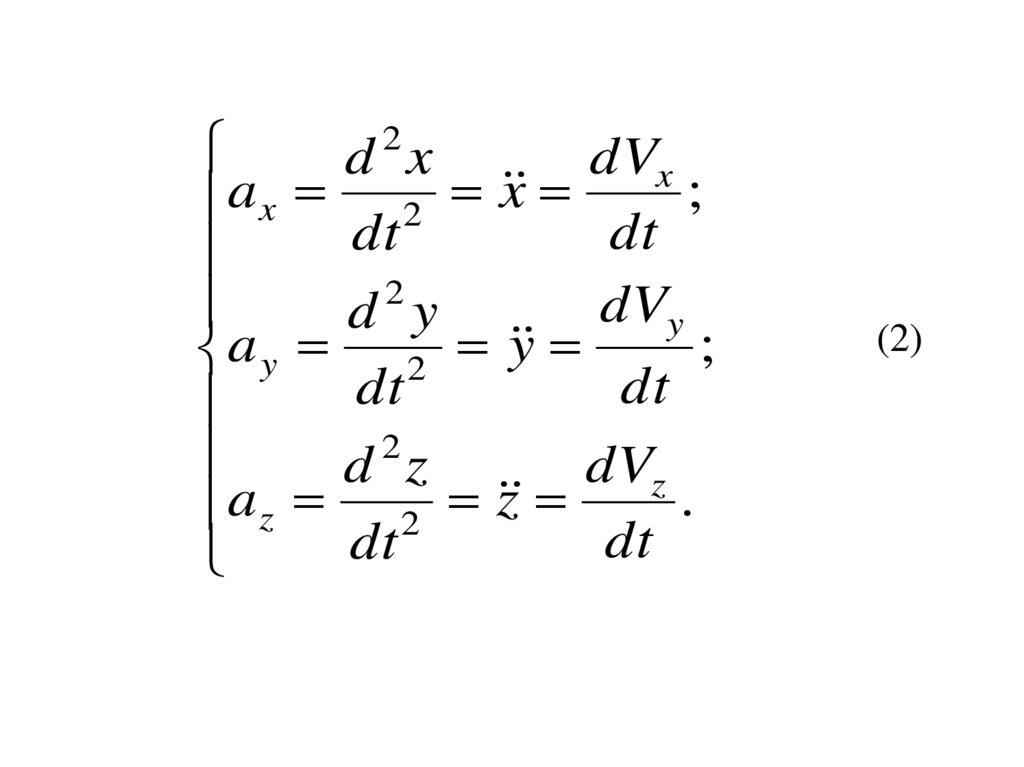











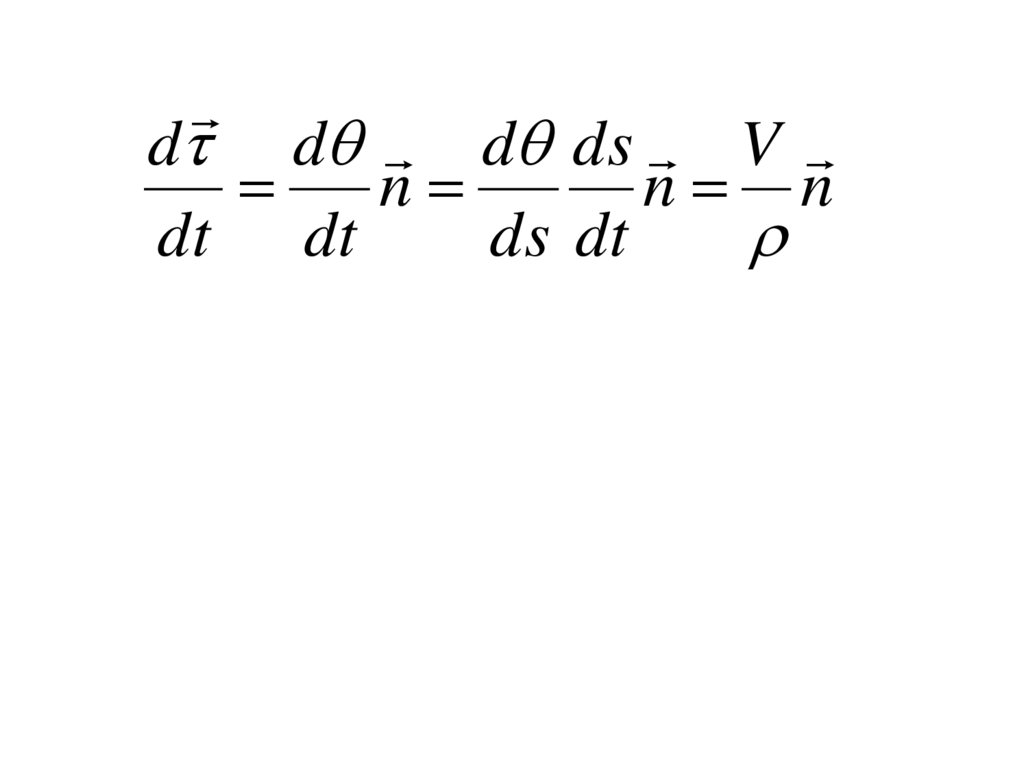


















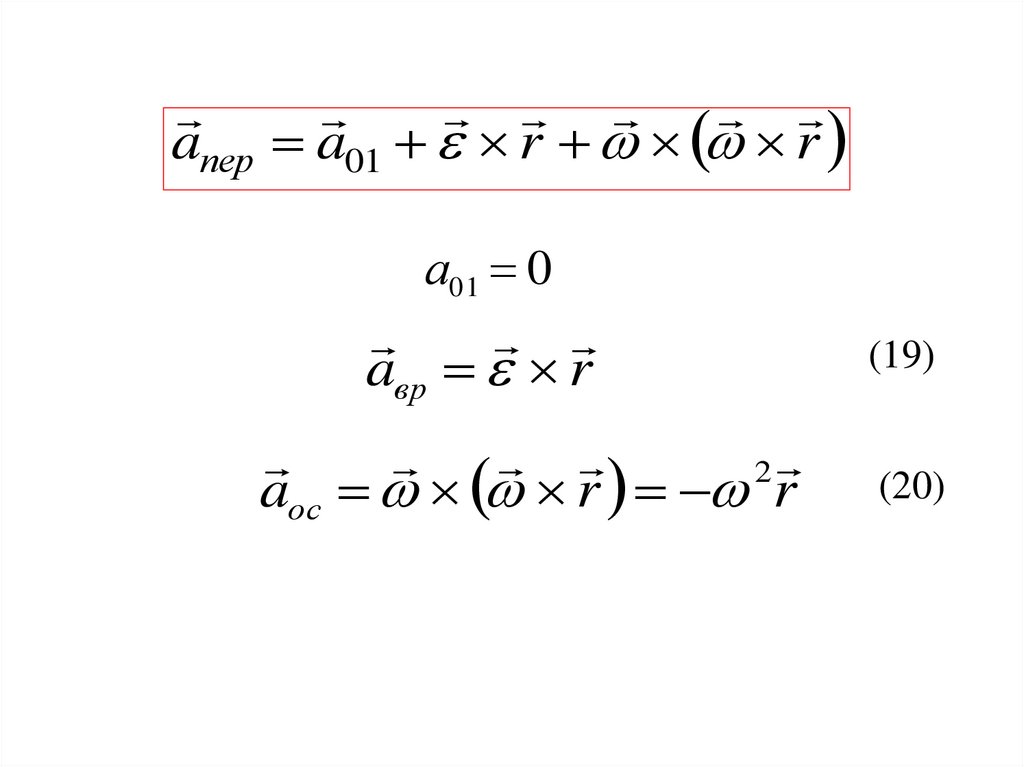





 Физика
Физика








