Похожие презентации:
Пропорциональные отрезки
1.
2.
Среднее арифметическоечисел m и n называется число
а, равное полусумме чисел
mиn
n m
а
2
Число a называется средним
геометрическим (или средним
пропорциональным) для чисел
m и n , если
выполняется равенство
a m n
3.
№1. Найдите среднее арифметическое исреднее геометрическое чисел 3 и 12
3 12
7,5
2
3 12 6
№2. Найти длину среднего
пропорционального (среднего
геометрического) отрезков MN и KP, если
MN = 9 см, KP = 16 см
12
см
9
16
a MN KP
4.
cC
bc
ac
h
a
A
D
B
b
Проекция
катета b
а на
на гипотенузу
Проекция катета
сгипотенузу с
5.
Катет прямоугольного треугольника есть среднеепропорциональное для гипотенузы и проекции
катета на гипотенузу.
C
АС АВ АD
BС АВ BD
b
a
h
bc
D
A
c
ac
a c ac
b c b c
B
6.
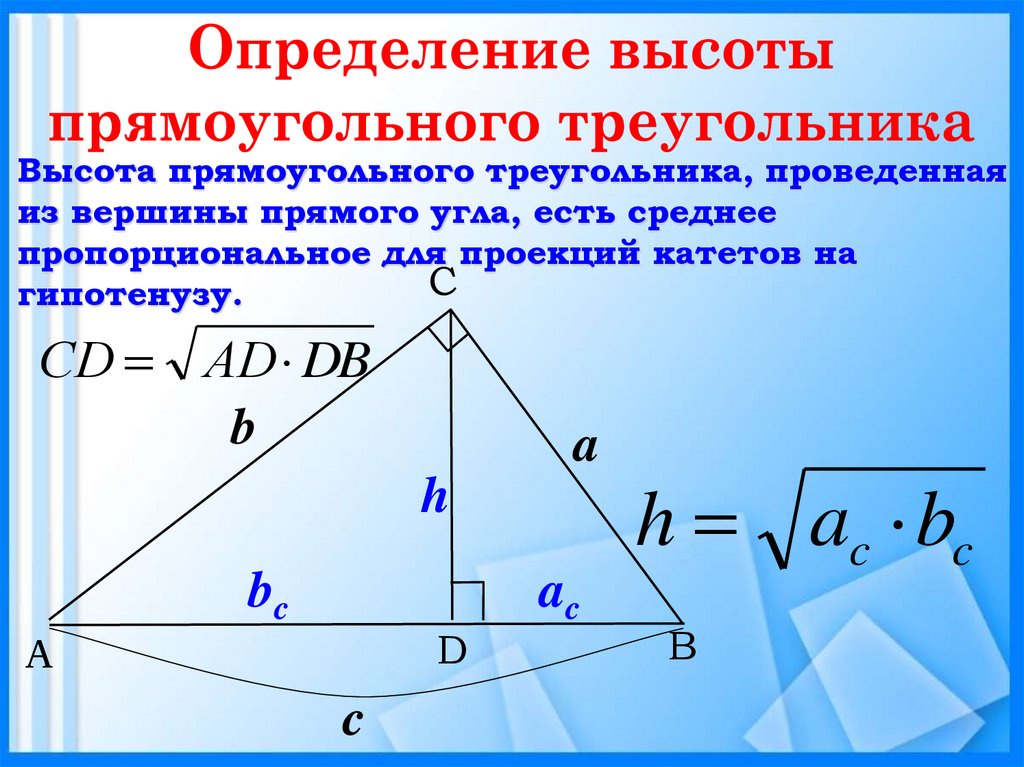
Высота прямоугольного треугольника, проведеннаяиз вершины прямого угла, есть среднее
пропорциональное для проекций катетов на
C
гипотенузу.
СD АD DB
b
a
h
bc
D
A
c
ac
h ac bc
B
7.
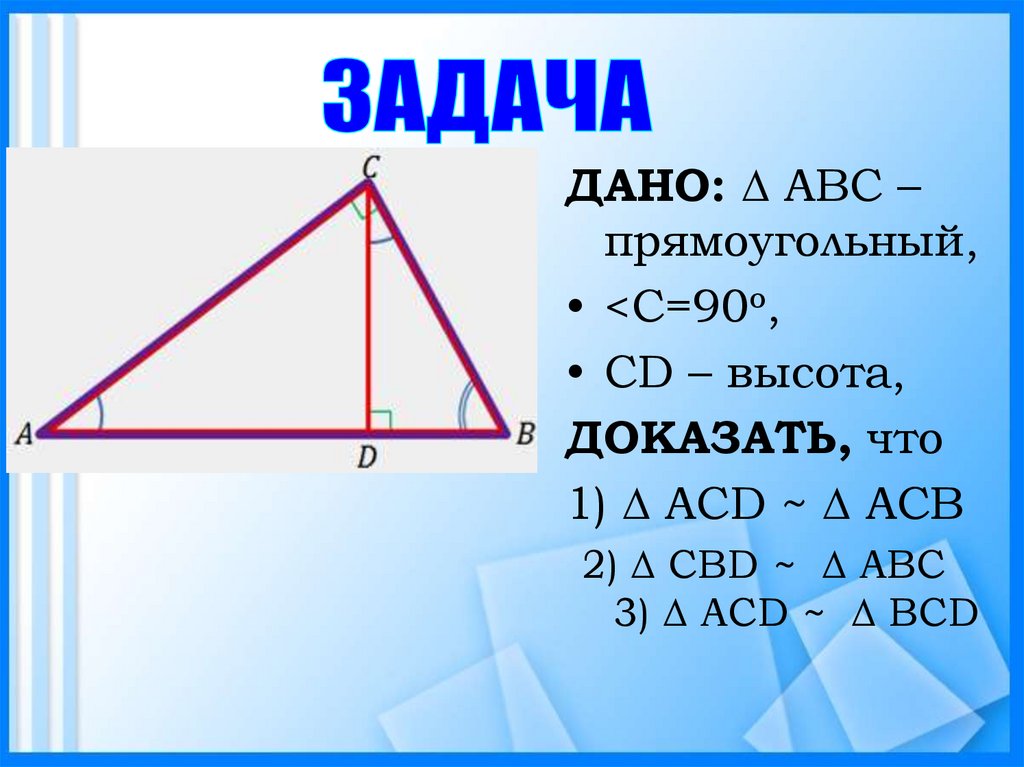
ДАНО: ∆ АВС –прямоугольный,
• <С=90о,
• СD – высота,
ДОКАЗАТЬ, что
1) ∆ АСD ~ ∆ АСB
2) ∆ CBD ~ ∆ ABC
3) ∆ АСD ~ ∆ BCD
8. ДОКАЗАТЕЛЬСТВО
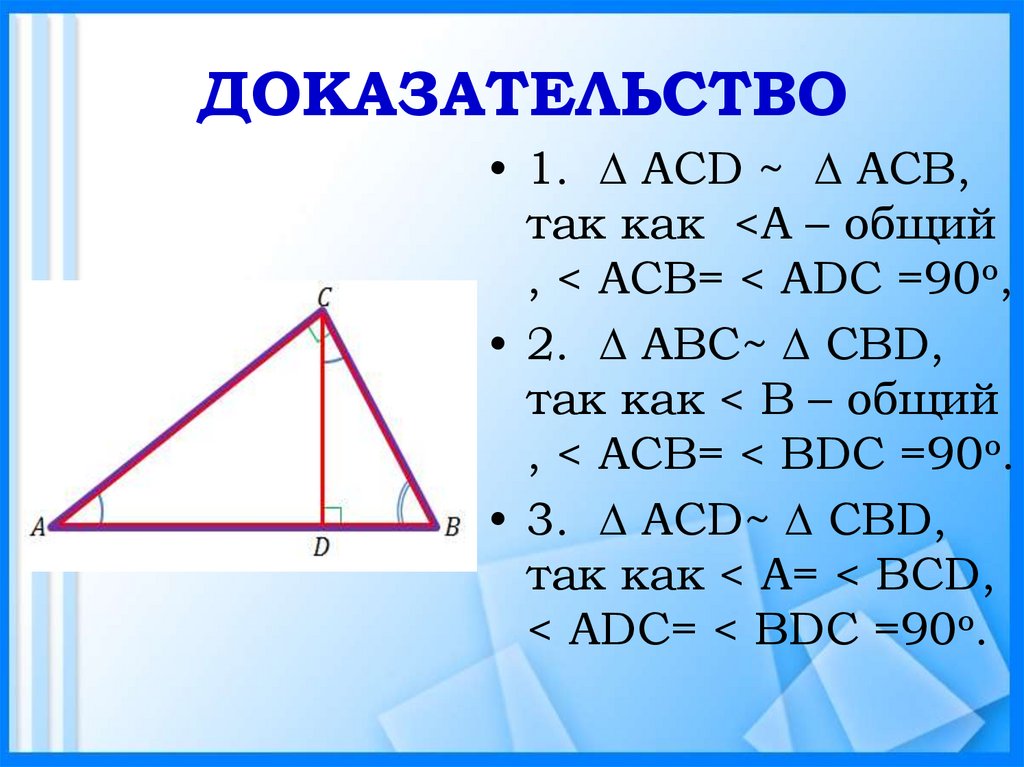
ДОКАЗАТЕЛЬСТВО• 1. ∆ АСD ~ ∆ АСB,
так как <А – общий
, < АСВ= < АDC =90о,
• 2. ∆ АBС~ ∆ СBD,
так как < B – общий
, < АСВ= < BDC =90о.
• 3. ∆ АСD~ ∆ СBD,
так как < A= < BCD,
< АDС= < BDC =90о.





 Математика
Математика








