Похожие презентации:
Комплексные числа и действия над ними
1.
Тема «Комплексные числа и действия над ними»Основные понятия:
1.
2.
3.
4.
5.
6.
7.
Определение комплексного числа. Алгебраическая
форма комплексного числа.
Геометрическое изображение комплексного числа.
Действия над комплексными числами, заданными в
алгебраической форме.
Тригонометрическая форма комплексного числа.
Действия над комплексными числами, заданными в
тригонометрической форме.
Возведение в степень комплексного числа.
Извлечение корней из комплексного числа.
Завершить
2.
Определение комплексного числа.Алгебраическая форма комплексного числа.
1.
Комплексным числом называют упорядоченную пару a; b
действительных чисел а и b, алгебраической формой
которого является z a b i
а = Re z – действительная часть комплексного числа,
b = Im z – мнимая часть комплексного числа,
i – мнимая единица ( i 1, i 2 1 ).
Комплексное число z a b i называют сопряженным
к комплексному числу z a b i
назад
3.
2. Геометрическое изображение комплексного числа.Выберем ДПСК, в которой
комплексному числу
z a b i
сопоставим точку M a; b
Плоскость, точки которой отождествлены с комплексными
числами, называют комплексной плоскостью.
Пример 1.
назад
4.
Пример 1. Изобразить на комплексной плоскостиследующие комплексные числа
z1 2
z2 3i
z3 1 2i
z4 3 i
Решение
назад
5.
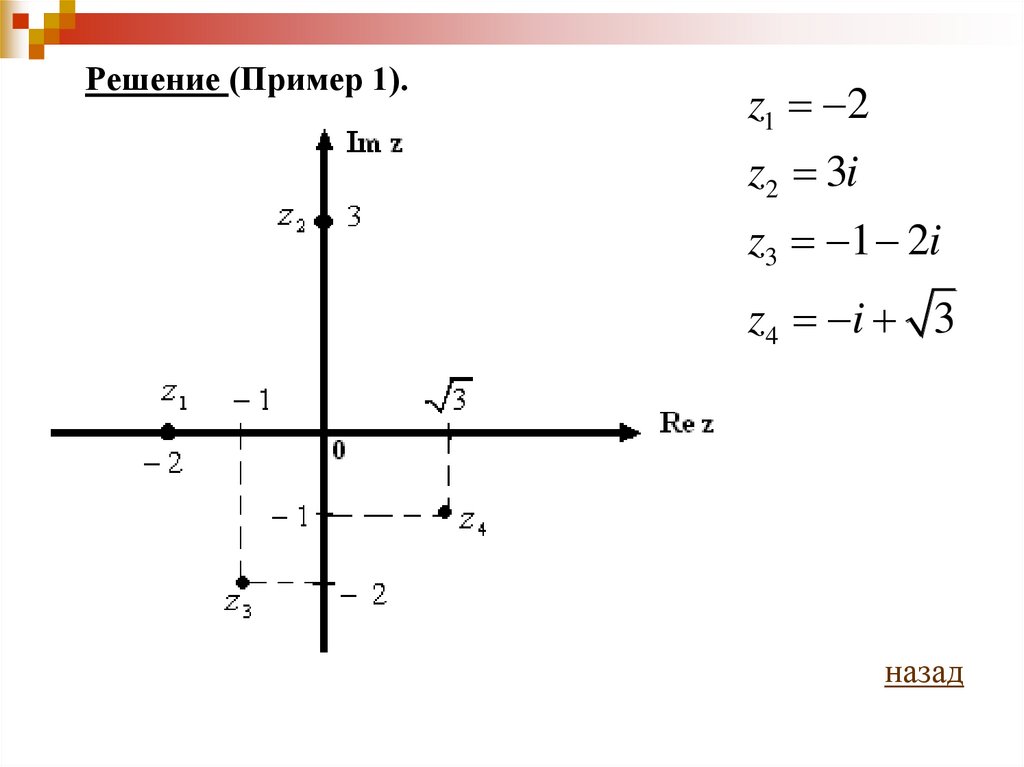
Решение (Пример 1).z1 2
z2 3i
z3 1 2i
z4 i 3
назад
6.
3. Действия над комплексными числами, заданными валгебраической форме.
Сложение (вычитание) комплексных чисел
Умножение комплексных чисел
Деление комплексных чисел
Нахождение обратного числа к комплексному числу
Рассмотрим два комплексные числа
z a b i и z c d i
1
2
назад
7.
Сложение (вычитание):z1 z2 a b i c d i a c b d i
z1 z2 a b i c d i a c b d i
z1 2i 3, z2 3 4i
z1 z2 , z1 z2 , z2 z1
Пример 2. Для
вычислить
Решение
назад
8.
Решение (Пример 2):z1 z2 3 2i 3 4i 3 3 2 4 i 2i
z1 z2 3 2i 3 4i 6 6i
z2 z1 3 4i 3 2i 6 6i
назад
9.
Умножение:z1 z2 a b i c d i ac bd bc ad i
Пример 3. Для z1 2i 3,
z2 3 4i
вычислить
z1 z2
Решение
назад
10.
Решение (Пример 3):z1 z2 3 2i 3 4i
3 3 3 4i 2i 3 2i 4i
8i 2 8 1 8
1 18i
назад
11.
Деление:z1 a b i ac bd bc ad
2
2
i
2
2
z2 c d i c d
c d
z1
Пример 4. Для z1 2i 3, z2 3 4i вычислить
z2
Решение
назад
12.
Решение (Пример 4):z1 3 2i 3 2i 3 4i
z2
3 4i
3 4i 3 4i
9 12i 6i 8i 2
17 6
i
2
9 16i
25 25
16 1 16
назад
13.
Нахождение обратного числа к комплексному числу :1
1
a
b
2
2
i
2
2
z1 a b i a b a b
1 1
,
Пример 5. Для z1 2i 3, z2 3 4i вычислить
z1 z 2
Решение
назад
14.
Решение (Пример 5):1
1
1
3 2i
z1 3 2i 3 2i 3 2i
3 2i
3 2
i
2
9 4i
13 13
1
1
1 3 4i
z2 3 4i 3 4i 3 4i
3 4i
3
4
i
2
9 16i
25 25
назад
15.
4. Тригонометрическая форма комплексного числа.Модуль (длина отрезка ОМ):
r z OM a 2 b2
Аргумент:
Arg z arg z 2 k , k Z ,
ãäå arg z , 0; 2
- главное значение аргумента.
Тогда a r cos , b r sin
a b i r cos i sin
- тригонометрическая форма комплексного числа
Пример 6.
назад
16.
Пример 6. Представить следующие комплексные числа втригонометрической форме
z1 2
z2 3i
z3 1 i
z4 3 i
Решение
назад
17.
Решение (Пример 6).r z2 0 3 3
2
r z1
2 0 2
2
2
2
z1 2 cos i sin
z2 3 cos i sin
2
2
2
далее
18.
Решение (Пример 6).r z3
1 1 2
2
2
3
4
3
3
z3 2 cos
i sin
4
4
r z4
3 1 2
2
2
11
6
11
11
z4 2 cos
i sin
6
6
назад
19.
5. Действия над комплексными числами, заданными втригонометрической форме.
Рассмотрим комплексные числа
z r cos i sin и z
1
1
2
r2 cos i sin
Сложение:
z1 z2 r1 cos r2 cos i r1 sin r2 sin
Вычитание:
z1 z2 r1 cos r2 cos i r1 sin r2 sin
далее назад
20.
Умножение:z1 z2 r1 cos i sin r2 cos i sin
r1r2 cos i sin
r1 cos i sin
z2 r2 cos i sin
Деление: z1
r1 cos i sin cos i sin
r2 cos i sin cos i sin
r1
cos i sin
r2
назад
21.
6. Возведение в степень комплексного числа.Рассмотрим возведение в степень мнимой единицы:
i1 i, i 2 1, i 3 i, i 4 1, i 5 i è ò.ä.
i 4 k 1, i 4 k 1 i, i 4 k 2 1, i 4 k 3 i, k 0,1...
2
3
При возведении a b i и a b i
пользуются формулами сокращенного умножения.
Пример 7. Вычислить
i i
2
3
1) 73 68 ; 2) 3 5i ; 3) i 2
i i
80
Решение
123
назад
22.
Решение (Пример 7):i i
i
i
i i 1 i
1) 73 68 4 18 1 4 17 0 1 0
1
i i
i
i
i i
i 1
80
4 20 0
123
4 30 3
0
3
2) 3 5i 9 30i 25i 2 16 30i
2
25 1 25
3) i 2 i 3 i 2 3 i 2 2 2 11i
3
3
2
i
6
2
12 i
3
8
назад
23.
Замечание. При возведении a b i пользуютсяформулой бином Ньютона или формулой возведения в
степень комплексного числа (формула Муавра),
заданного в тригонометрической форме.
n
Формула Муавра:
z r cos i sin r n cos n i sin n
n
n
Пример 8. Вычислить 3 i 1
2
2
6
Решение
назад
24.
Решение (Пример 8):1
3
1) Представим z
i в тригонометрической форме:
2 2
2
r z 1,
3
2
2
z cos
i sin
3
3
2) Воспользуемся формулой Муавра:
6
6
3 1
2
2
2
2
i
cos
i
sin
cos
6
i
sin
6
2
3
3
3
3
2
cos 4 i sin 4 1
назад
25.
7. Извлечение корней из комплексного числа.Извлечение квадратных корней:
a b i u v i
u v i a b i
2
2 a a 2 b2
u
2
2
u v a
2
2uv b
2 a a 2 b 2
v
2
Пример 9. Вычислить
5 12i
Решение
далее назад
26.
Решение (Пример 9):назад
27.
Извлечение корня n-ой степени:n
z n r cos i sin
2 k
2 k
r cos
i sin
, k 0,1,..., n 1.
n
n
n
Пример 10. Вычислить
3
1
Решение
назад
28.
Решение (Пример 10):1) Представим
z 1
в тригонометрической форме
r z 1,
z cos i sin
2) Воспользуемся формулой извлечения корня n-ой степени:
3
1 3 cos i sin
2 k
2 k
1 cos
i sin
, k 0,1, 2.
3
3
3
далее
29.
Решение (Пример 10):3) Рассмотрим случаи для k:
если k 0 z1 cos
2 0
i sin
2 0
3
3
1
3
cos i sin i
.
3
3 2
2
2 1
2 1
если k 1 z2 cos
i sin
3
3
cos i sin 1.
если k 2 z3 cos 2 2 i sin 2 2
3
3
5
5 1
3
cos
i sin
i
.
3
3 2
2
назад
30.
Спасибо за внимание!Не забывайте готовиться к
лекциям и семинарам!
Удачи!





























 Математика
Математика








