Похожие презентации:
Algorithms for solving NP problems
1.
ALGORITHMS FOR SOLVINGNP PROBLEMS
2.
The purpose of presentation is to acquaint the listenerswith the example of the problem of finding a Hamiltonian
cycle in a graph and the «Knapsack problem»:
• with the concept of «NP complexity problems»
• with algorithms for solving these problems
3.
• Cryptography is the art and science of protecting messages with encryption.• A cryptographic algorithm (or cipher, or key) is a mathematical function or
two mathematical related functions (one for encryption, the other for
decryption).
4.
ALGORITHM RELIABILITY• Unconditional reliability - recovery of the plaintext or key is impossible
with any amount of cipher text received by the cryptanalyst.
• The algorithm is reliable if it is cracked will cost more than the cost of
encrypted data take longer than keeping the data private the
amount of data required exceeds the amount of data encrypted with
a key.
5.
COMPLEXITY THEORY• «Information theory claims that almost all cryptographic algorithms can be
broken. Complexity theory determines whether they can be hacked before
the thermal death of the universe».
Bruce Schneier. Applied Cryptography. Protocols, Algorithms, and
Source Code in C
6.
COMPLEXITY THEORY DEFINES AND CLASSIFIES• complexity of algorithms
• the complexity of the tasks themselves
7.
P VS NP PROBLEM8.
PROPERTIES OF NP-HARD PROBLEMS:• NP-hard problem cannot be solved by existing algorithms;
• if a polynomial solution to any such problem is found, then
all problems from the NP class will be quickly solvable.
9.
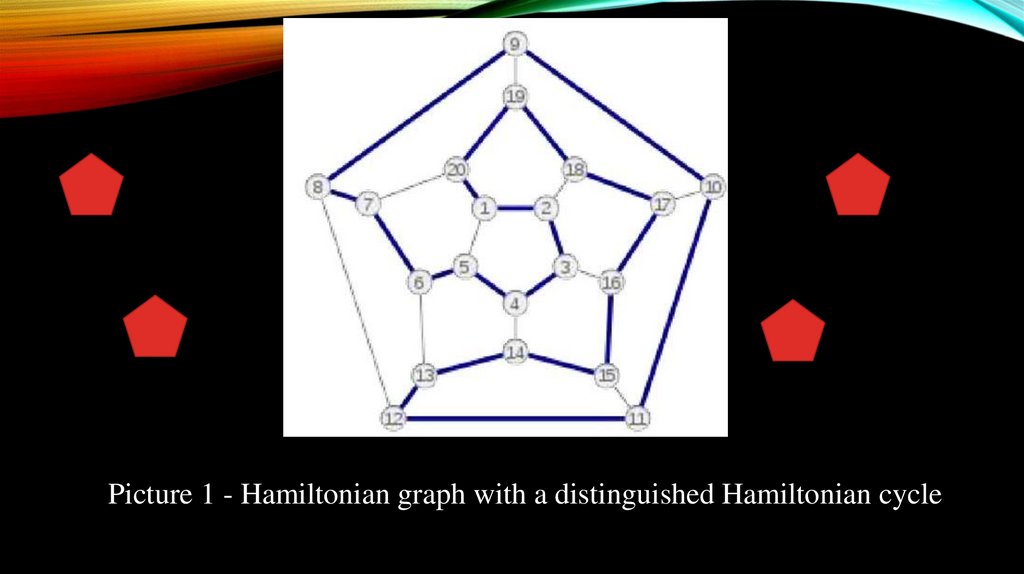
Picture 1 - Hamiltonian graph with a distinguished Hamiltonian cycle10.
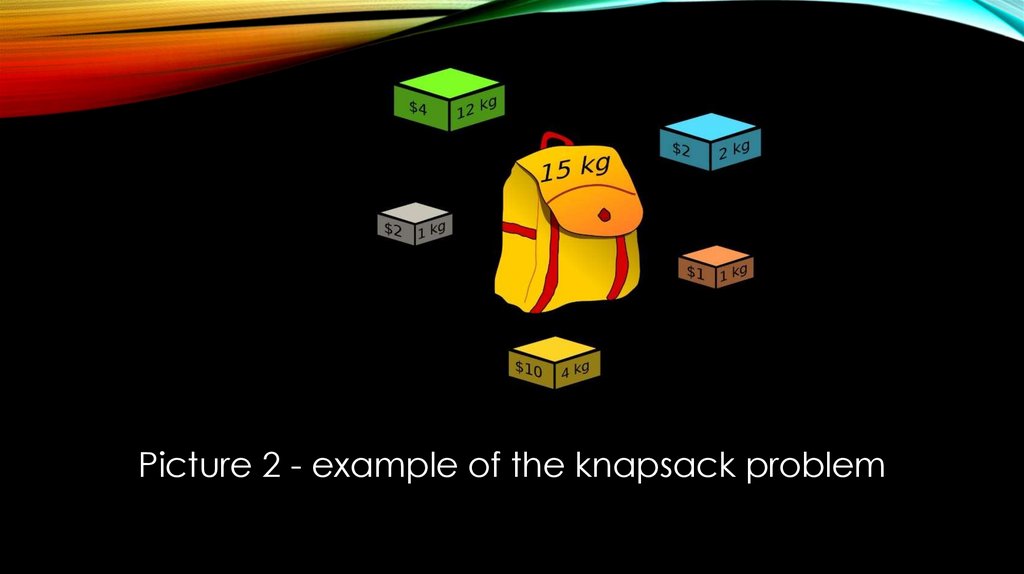
Picture 2 - example of the knapsack problem11.
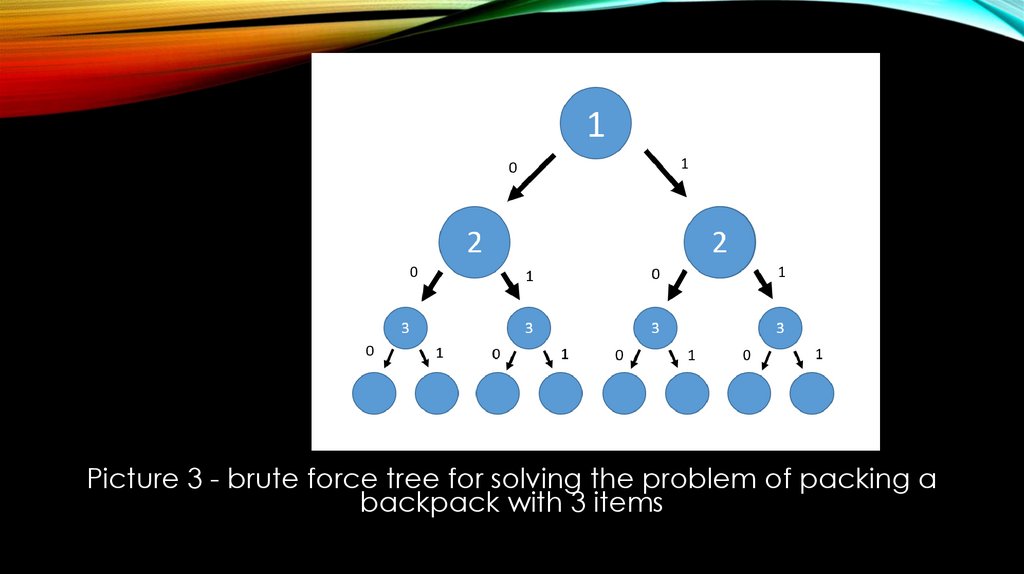
Picture 3 - brute force tree for solving the problem of packing abackpack with 3 items
12.
TABLE 1 - CONDITION OF THE PROBLEM OF PACKING A BACKPACKItem number
Value
Weight
1
3
5
2
5
10
3
4
6
4
2
5
13.
WeightObjects
Picture 6 - coordinate system illustrating the implementation
of the dynamic











 Математика
Математика








