Кинематика гармонических колебаний (тема 5.1 )

1.

Тема 4.1. «Магнитное поле»
ФГБОУ ВО СИБИРСКАЯ ПОЖАРНО-СПАСАТЕЛЬНАЯ АКАДЕМИЯ
ГПС МЧС РОССИИ
Кафедра физики, математики и
информационных технологий
Раздел 5. «Физика колебаний и волн»
Тема 5.1.1 Лекция
« Кинематика Гармонических колебаний»
Тема 5.1 «Кинематика гармонических колебаний»
1

2.

ФГБОУ ВО СИБИРСКАЯ ПОЖАРНО-СПАСАТЕЛЬНАЯ
АКАДЕМИЯ ГПС МЧС РОССИИ
КОЛЕБАНИЯ в ПОЖАРНОМ ДЕЛЕ:
1 Гидроударные явления в пожарной струе,
элементах НРС и трубах ППВ
2 Движение элементов двигателей (электро и
внутр. сгорания) Пожарных Автомобилей
3 Колебания земной коры при землетрясениях
4 Цунами и морские волны, молнии, грозы, смерчи,
торнадо….
5 Оглушительный рев двигателей и турбин
6 Колебательные процессы в пож-насосах ,
мотопомпах, электродвигателях
7 Инфракрасное излучение от горящих объектов и
при процессы при лучистом теплообмене
8 Использование теории э/м колебаний (спектральный анализ) в пожарной криминалистике.
Тема 5.1.2 «Кинематика гармонических колебаний»
2

3.

Тема 4.1. «Магнитное поле»
ФГБОУ ВО СИБИРСКАЯ ПОЖАРНО-СПАСАТЕЛЬНАЯ
АКАДЕМИЯ ГПС МЧС РОССИИ
Учебные вопросы:
1. Гармонические колебания и их
характеристики.
2. Примеры гармонических колебаний.
3. Сложение гармонических колебаний.
Тема 5.1. «Кинематика гармонических колебаний»
3

4.

1. Гармонические колебания и их
характеристики
Колебаниями называют движения или
процессы, обладающие повторяемостью
во времени.
Колебания называют свободными (или
собственными), если они совершаются за
счет первоначально сообщенной энергии
при отсутствии последующих внешних
воздействий.
Тема 5.1 «Кинематика гармонических колебаний»
4

5.

Колебания, возникающие за счет внешней,
периодически
меняющейся
силы,
называют вынужденными.
Колебания, при которых колеблющаяся
величина изменяется со временем по закону
синуса или косинуса, называют
гармоническими.
Тема 5.1 «Кинематика гармонических колебаний»
5

6.

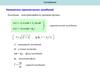
Уравнение гармонического колебания
x A sin t ,
А – амплитуда колебания;
- циклическая частота;
( t + ) - фаза колебания;
- начальная фаза колебания.
Тема 5.1. «Кинематика гармонических колебаний»
6

7.

Время
одного
полного
называется периодом:
T
2
колебания
.
число полных колебаний в единицу времени,
называется частотой:
1
n .
T 2
Тема 5.1. «Кинематика гармонических колебаний»
7

8.

Скорость и ускорение при гармонических
колебаниях:
v x A cos t ,
a x v
A sin t x
2
Тема 5.1 «Кинематика гармонических колебаний»
2
8

9.

Сила, действующая на колеблющуюся
материальную точку массой m:
F ma m x.
2
Эта сила, независимо от физической
природы, носит название упругой силы.
Тема 5.1 «Кинематика гармонических колебаний»
9

10.

Уравнение движения для гармонических
колебаний:
ma m x,
2
x x 0
2
(1)
Система,
совершающая
колебания,
описываемые таким уравнением, называ-ется
гармоническим осциллятором.
Тема 5.1 «Кинематика гармонических колебаний»
10

11.

Гармонические колебания изображают
графически
методом векторных диаграмм.
A
O
x
Тема 5.1 «Кинематика гармонических колебаний»
x
11

12.

Кинетическая энергия
гармонических колебаний:
2
mv
m 2 2
2
Ek
A cos t
2
2
Максимальное значение кинетической
энергии:
mA
2
2
Ek max
Тема 5.1 «Кинематика гармонических колебаний»
2
12

13.

Потенциальная энергия
гармонических колебаний равна работе
упругой силы:
m x
E p Fdx
2
m 2 2 2
E p A sin t
2
2
E p max Еk max
2
mA
2
Тема 5.1 «Кинематика гармонических колебаний»
2
2
13

14.

Полная энергия колебаний равна:
mA
E Ek E p
2
2
2
Полная энергия
при гармонических колебаниях остается
постоянной величиной.
Тема 5.1. «Кинематика гармонических колебаний»
14

15.

2. Примеры гармонических колебаний
Пружинный маятник
F = kx,
х
k
где k – жесткость
пружины.
m
0
х
mx kx
Тема 5.1. «Кинематика гармонических колебаний»
15

16.

k
x x 0
m
Сопоставляя с уравнением (1), находим
циклическую частоту и период колебаний
пружинного маятника:
k
,
m
m
T 2
k
Тема 5.1 «Кинематика гармонических колебаний»
16

17.

Потенциальная энергия
пружинного маятника:
m x
kx
Ep
2
2
2
2
Тема 5.1 «Кинематика гармонических колебаний»
2
17

18.

Математический маятник
F mg sin ,
l
T
mg
F 0
х
x
sin ,
l
mg
ma
x.
l
Тема 5.1 «Кинематика гармонических колебаний»
18

19.

g
x x 0
l
Сопоставляя с уравнением (1), находим:
g
,
l
l
T 2
.
g
Тема 5.1 «Кинематика гармонических колебаний»
19

20.

Физический маятник
d
О
С
mg
M J J ,
M mgd sin
d – расстояние от оси до
центра масс маятника,
J – момент инерции.
Тема 5.1 «Кинематика гармонических колебаний»
20

21.

При малых углах sin
J mgd ,
mgd
0.
J
Тема 5.1 «Кинематика гармонических колебаний»
21

22.

Сравнивая с уравнением (1), находим:
mgd
,
J
J
T 2
mgd
Тема 5.1 «Кинематика гармонических колебаний»
22

23.

3. Сложение гармонических колебаний
Сложение колебаний
одного направления и частоты
x A cos t
x A cos t
1
2
1
2
Тема 5.1 «Кинематика гармонических колебаний»
1
2
23

24.

2
х1
х
1
2 1
х2
х
уравнение результирующего колебания:
x x x A cos t ,
1
2
Тема 5.1 «Кинематика гармонических колебаний»
24

25.

A A A 2 A A cos
2
2
1
2
2
1
2
2
1
A sin A sin
tg
A cos A cos
1
1
1
2
1
2
2
2
Точка, участвуя в двух гармонических колебаниях
одного направления и одинаковой частоты,
совершает гармоническое колебание в том же
направлении и с той же частотой, что и
складываемые колебания.
Тема 5.1 «Кинематика гармонических колебаний»
25

26.

Сложение взаимно перпендикулярных
колебаний
x A cos t
y B cos t ,
x
cos
t
A
y
cos t cos t cos sin t sin
B
Тема 5.1 «Кинематика гармонических колебаний»
26

27.

x
sin t 1
A
2
2
2
x
2 xy
y
cos
sin
A
AB
B
2
2
2
траектория результирующего колебания
имеет форму эллипса.
Тема 5.1 «Кинематика гармонических колебаний»
27

28.

а)
m
( m = 0, 1, 2, …).
Тогда sin = 0 и cos = 1,
и эллипс вырождается
в отрезок прямой:
у
B
y x
A
Тема 5.1. «Кинематика гармонических колебаний»
В
-А
0
-В
А
х
28

29.

Амплитуда результирующего колебания:
A A B
2
2
1
Прямая составляет с осью х угол:
B
arctg
A
Тема 5.1. «Кинематика гармонических колебаний»
29

30.

б)
2m 1
2
( m = 0, 1, 2, …).
В этом случае sin = 1 и cos = 0, и
траектория точки - эллипс
у
В
2
2
x
y
1
2
2
A
B
Тема 5.1. «Кинематика гармонических колебаний»
А
х
30

31.

Замкнутые траектории, прочерчиваемые
точкой, совершающей два взаимно
перпендикулярных колебания, называют
фигурами Лиссажу.
Тема 5.1. «Кинематика гармонических колебаний»
31

32.

ЗАКЛЮЧЕНИЕ:
Итак,
мы изучили следующие учебные
вопросы:
1. Гармонические колебания и их
характеристики.
2. Примеры гармонических колебаний.
3. Сложение гармонических колебаний.
Тема 5.1. «Кинематика гармонических колебаний»
32

33.

Задание на самоподготовку:
1. Изучить рекомендуемую литературу
§ § 140 – 145.
Рекомендуемая литература:
1. Трофимова Т.И. Курс физики.
М.: изд-во «Академия», 2012
Тема 5.1. «Кинематика гармонических колебаний»
33