Похожие презентации:
Гармонические колебания и их характеристики
1.
15. Гармонические колебания иих характеристики
2.
Колебаниями или колебательными движенияминазываются движения или изменения состояния,
обладающие той или иной степенью повторяемости во
времени.
3.
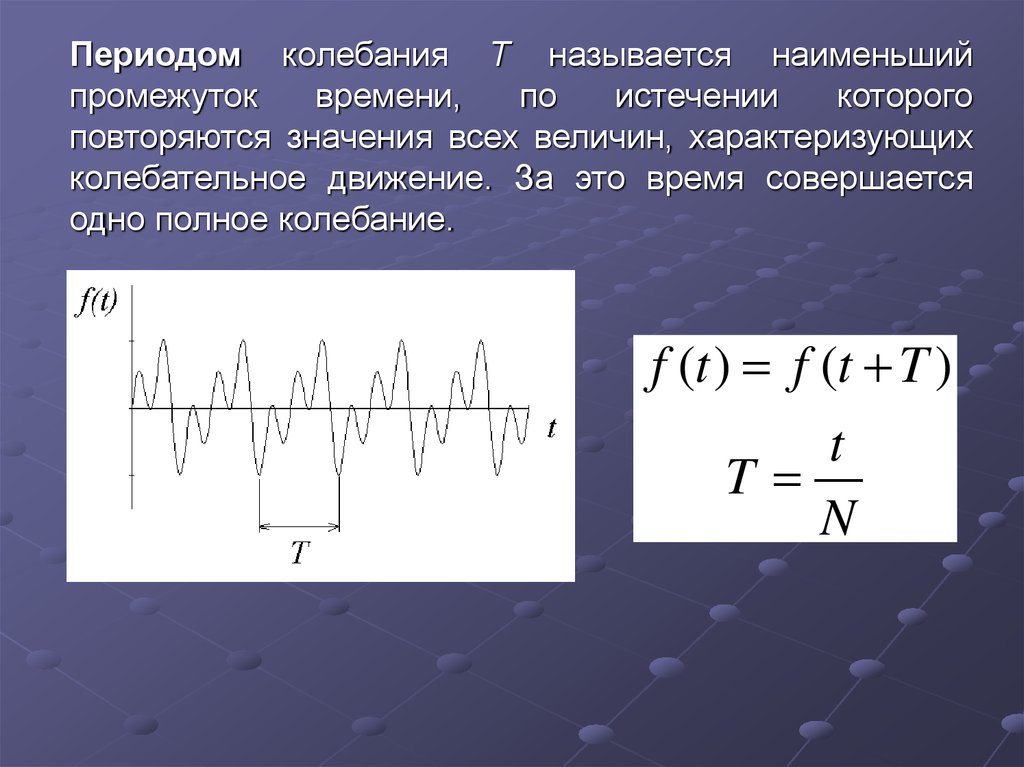
Периодом колебания Т называется наименьшийпромежуток
времени,
по
истечении
которого
повторяются значения всех величин, характеризующих
колебательное движение. За это время совершается
одно полное колебание.
f (t ) f (t T )
t
T
N
4.
Частотойпериодических
колебаний
называется число полных колебаний, которые
совершаются за единицу времени:
N 1
t T
5.
Циклической (круговой) частотой периодическихколебаний называется число полных колебаний,
которые совершаются за 2 секунд:
2
2
T
6.
Получить уравнение простейшего колебания можно,установив
аналогию
между
вращательным
и
колебательным движением.
При вращении с постоянной
скоростью проекция вектора
на ось Х равна:
x A cos
t 0
Угол поворота определяет значение х в данный момент
времени и называется фазой колебания.
7.
В результате простейшее периодические колебанийсовершается по гармоническому закону:
x A cos( t 0 )
8.
Скорость при гармоническом колебанииx A sin( t 0 )
0 sin( t 0 )
0 A
– амплитуда скорости.
9.
Ускорение при гармоническом колебанииa x A cos( t 0 )
2
a 0 A
2
- амплитуда ускорения.
10.
0 0x A cos( t 0 )
A sin( t 0 ) A cos( t 0 2)
a A 2 cos( t 0 )
Графическое изображение гармонических колебаний
посредством
вращающегося
вектора
амплитуды
называется методом векторных диаграмм.
11.
Графическое изображение гармонических колебанийпосредством
вращающегося
вектора
амплитуды
называется методом векторных диаграмм.
12.
Ускорение и координата при гармонических колебаниях влюбой момент времени связаны соотношением
a x
2
или
x x
2
x x 0
2
представляющим
собой
дифференциальное
уравнение гармонических колебаний. Решением
уравнения является гармоническая функция.
13.
Согласно формуле Эйлераei cos i sin
i 1
Уравнение гармонического колебания в комплексной
форме имеет вид
i t 0
~
x x0 e
Физический смысл имеет лишь действительная
часть, обозначаемая
~
Re x x0 cos t 0
14. 16. Квазиупругая сила. Период колебаний пружинного, математического и физического маятников.
15.
Пружинный маятник. Колебания груза массой m напружине жесткостью k совершаются под действием
силы упругости пружины
F kx
Ускорение телу сообщает сила упругости
kx ma
kx mx
k
x x 0
m
k
2
m
k
m
m
T 2
k
16. Тело совершает гармонические колебания в случае действия на него квазиупругой возвращающей силы. Для определения частоты необходимо уста
Тело совершает гармонические колебания вслучае действия на него квазиупругой
возвращающей силы.
Для определения частоты необходимо
установить квазиупругий характер
возвращающей силы, определить k.
k
квазиупруг ий фактор
m
масса системы
17.
Математический маятник представляет собойматериальную точку, подвешенную на невесомой
нерастяжимой нити и совершающую движение в
вертикальной плоскости под действием
силы
тяжести
W mgh
l l h x
2
2
2
2
x
h
2l
2
2
mgx
kx
W
2l
2
18.
mgk
l
k
m
g
l
l
T 2
g
l – длина подвеса,
g – ускорение свободного падения.
19. Физический маятник представляет собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром
масс этоготела,
или
неподвижной
оси,
перпендикулярной
направлению действия сил и не проходящей через центр
масс этого тела.
20. Колебания происходят под действием момента силы тяжести.
M IM mgd sin
mgd sin I
sin
mgd I
mgd
I
21.
Для угла отклонения получаем дифференциальноеуравнение гармонических колебаний
mgd
0
I
mgd
I
22. l* - приведенная длина физического маятника
Период колебаний физического маятника*
I
l
T 2
2
mgd
g
I
l
md
*
l* - приведенная длина физического маятника
23. 17. Превращение и изменение энергии в системе
24.
Превращение энергии рассмотрим на примерепружинного маятника. Пусть колебания происходят по
закону
x A cos t
При гармонических колебаниях пружинного маятника
происходят превращения потенциальной энергии
упругой деформации
2
kx
U
2
в его кинетическую энергию и наоборот
m
E
2
2
25.
Полнаяэнергия
колебательной
определяется суммой энергий:
системы
m 2 kx2 m( A sin t ) 2 k ( A cos t ) 2
W
2
2
2
2
m 2 A2 sin 2 t m 2 A2 cos2 t m 2 A2
2
2
2
m A
W
2
2
2
26.
Колебание энергий происходит с удвоенной частотойпо сравнению с колебаниями координаты.
27. Колебания кинетической и потенциальной энергии в колебательной системе происходит с удвоенной частотой 2.
Колебания кинетической и потенциальнойэнергии в колебательной системе происходит с
удвоенной частотой 2 .
m A
1
2
2
E
sin t E0 sin t W 1 cos 2 t
2
2
m 2 A2
1
2
2
U
cos t E0 cos t W 1 cos 2 t
2
2
2
2
28.
Превращенияэнергии
при
колебаниях
пружинного
маятника
происходят
в
соответствии
с
законом
сохранения
механической
энергии.
Максимальные
значения энергий равны друг другу:
2
m 0
kA
2
2
2
29.
В любой момент сумма кинетической ипотенциальной энергии постоянна и равна
полной энергии.
2
m 0
m
kx
kA
2
2
2
2
2
2
2




























 Физика
Физика








