Похожие презентации:
Криволинейный интеграл по координатам (2- рода). Лекция №13
1.
Криволинейный интеграл по координатам(2- рода).
Вычисление криволинейного интеграла при
различных способах задания кривой.
Лекция №13
2.
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПО КООРДИНАТАМ( II рода)
1. Задача, приводящая к понятию криволинейного
интеграла II рода
Пусть под действием силы F = {P(x,y,z); Q(x,y,z); R(x,y,z)} точка
перемещается по кривой (ℓ) из точки L1 в точку L2 .
ЗАДАЧА: Найти работу, которую совершает сила F.
Пусть (ℓ) = (L1L2) – простая (т.е. без кратных точек)
спрямляемая (т.е. имеющая длину) кривая в пространстве
Oxyz, и на кривой (ℓ) задана функция P(x,y,z).
3.
Разобьем кривую (ℓ) произвольным образом на nчастей точками M0=L1, M1, …, Mn=L2 в направлении от L1
к L2.
Пусть Mi(xi; yi; zi). Обозначим Δxi = xi – xi–1 (т.е. проекцию
дуги (Mi –1Mi) на ось Ox).
На каждой дуге (Mi–1Mi) выберем произвольную точку
Ni(ξi;ηiζi) и вычислим произведение P(Ni) · Δxi .
4.
Суммуn
I n ( M i , Ni ) P( Ni ) xi
i 1
назовем интегральной суммой для функции P(x,y,z) по
кривой (ℓ) по переменой x (соответствующей данному
разбиению кривой (ℓ) и данному выбору точек Ni).
5.
Пусть max M i 1M i , где ΔMi–1Mi – длина дуги (Mi–1Mi)1 i n
ОПРЕДЕЛЕНИЕ. Число I называется пределом интегральных сумм I n ( M i , N i ) при 0 , если для любого
0 существует 0 такое, что для любого разбиения кривой ( ) у которого , при любом выборе
точек N i выполняется неравенство
I n ( M i , Ni ) I .
Если существует предел интегральных сумм I n ( M i , Ni )
при 0 , то его называют криволинейным интегралом от функции P( x, y, z ) по переменнойx
по
кривой ( ) .
Обозначают:
P( x, y, z)dx
( )
( L2 )
или
P( x, y, z )dx
( L1 )
6.
Аналогично определяются интегралыQ( x, y, z)dy
и
( )
Сумму
R( x, y, z)dz
( )
P( x, y, z)dx Q( x, y, z)dy R( x, y, z)dz
( )
( )
( )
записывают в виде
P( x, y, z)dx Q( x, y, z)dy R( x, y, z)dz
( )
и называют криволинейным интегралом
координатам).
II рода (по
7.
СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛАII РОДА
Замечание: предполагаем, что все рассматриваемые в
свойствах интегралы существуют.
1. Криволинейный интеграл II рода зависит от направления
движения по кривой. При изменении направления обхода
кривой (L1L2) криволинейный интеграл II рода меняет
знак, т.е.
Pdx Qdy Rdz Pdx Qdy Rdz
( L1 L2 )
( L2 L1 )
2. Если кривая (ℓ) замкнута, то криволинейный интеграл II
рода не зависит выбора начальной точки L1, а зависит от
направления обхода кривой.
8.
Направление обхода замкнутой кривой, при котором область,лежащая «внутри» контура, остается слева по отношению
к движущейся точке, называют положительным.
Противоположное
ему
направление
называют
отрицательным.
На
плоскости
положительным
направлением
обхода
является
направление против хода часовой
стрелки.
Криволинейный интеграл II рода по замкнутому контуру в
положительном направлении обозначают:
Pdx Qdy Rdz
( )
В отрицательном направлении:
Pdx Qdy Rdz
( )
9.
3. ФИЗИЧЕСКИЙ СМЫСЛ криволинейного интеграларода.
II
Пусть F {P ( x, y , z ); Q ( x, y , z ); R ( x, y , z )} – сила, под действием которой точка перемещается по кривой ( ) из L1 вL2 .
Работа, которую при этом совершает сила F , будет равна
A
Pdx Qdy Rdz
( )
4. Постоянный множитель можно выносить за знак криволинейного интеграла II рода, т.е.
c Qdy c Qdy,
c Pdx c Pdx,
( )
( )
( )
c Rdz c Rdz.
( )
( )
( )
10.
5. Криволинейный интеграл II рода от алгебраическойсуммы двух (конечного числа) функций равен
алгебраической сумме криволинейных интегралов II рода
от этих функций, т.е.
P1 P2 dx P1dx P2dx
( )
( )
( )
Q1 Q2 dy Q1dy Q2dy
( )
( )
( )
R1 R2 dz R1dz R2dz
( )
( )
( )
6. Если кривая (L1L2) разбита точкой K на две части (L1K) и
(KL2), то
Pdx Qdy Rdz Pdx Qdy Rdz Pdx Qdy Rdz
( L1 L2 )
( L1 K )
( KL2 )
(свойство аддитивности криволинейного интеграла II
рода).
11.
3. Вычисление криволинейного интегралаII рода
Пусть простая (не имеющая кратных точек) кривая (ℓ)=(L1L2)
задана параметрическими уравнениями:
x = φ(t), y = ψ(t), z = χ(t), где α ≤ t ≤ β (L1↔α , L2↔β)
.
(2)
ТЕОРЕМА 1. Если (ℓ) – гладкая кривая, заданная
уравнениями (2) и функция P(x,y,z) непрерывна на (ℓ), то
P(x,y,z) интегрируема по переменной x по кривой (ℓ) и
справедливо равенство
P( x, y, z )dx P (t ), (t ), (t ) (t )dt
( )
Аналогичным образом вычисляются интегралы
Q( x, y, z)dy
( )
и
R( x, y, z)dz
( )
(3)
12.
СЛЕДСТВИЕ 2. Если (ℓ) = (L1L2) – гладкая кривая в плоскостиxOy , заданная уравнением y = φ(x) (где x ∊ [a;b], L1(a;
φ(a)) , L2(b; φ(b)) и функции P(x,y), Q(x,y) непрерывны на
(ℓ), то существует криволинейный интеграл II рода и
справедливо равенство b
P( x, y)dx Q( x, y)dy P x, ( x) Q x, ( x) ( x) dx
( )
a
ТЕОРЕМА 3 (достаточные условия существования
криволинейного интеграла II рода).
Если (ℓ) – кусочно-гладкая спрямляемая кривая и функции
P(x,y,z), Q(x,y,z), R(x,y,z) кусочно-непрерывны на (ℓ) , то
существует интеграл
P( x, y, z)dx Q( x, y, z)dy R( x, y, z)dz
( )
13.
криволинейный интеграл 2-города зависит от направления
интегрирования, причём:
14.
ПримерВычислить криволинейный
интеграл
от точки
, где
до точки
– отрезок прямой
. Выполнить чертёж.
Решение: на первом шаге нам нужно
найти уравнение прямой, которая содержит
отрезок
. Составим его по двум точкам:
15.
область определения подынтегральныхфункций – в данном примере
, и поэтому
линия интегрирования не должна пересекать
координатные оси
Криволинейный интеграл 2-го рода тоже сводится к
определённому интегралу с «избавлением» либо от
всех «игреков», либо от всех «иксов».
16.
Подставимв подынтегральное выражение
Ответ:
17.
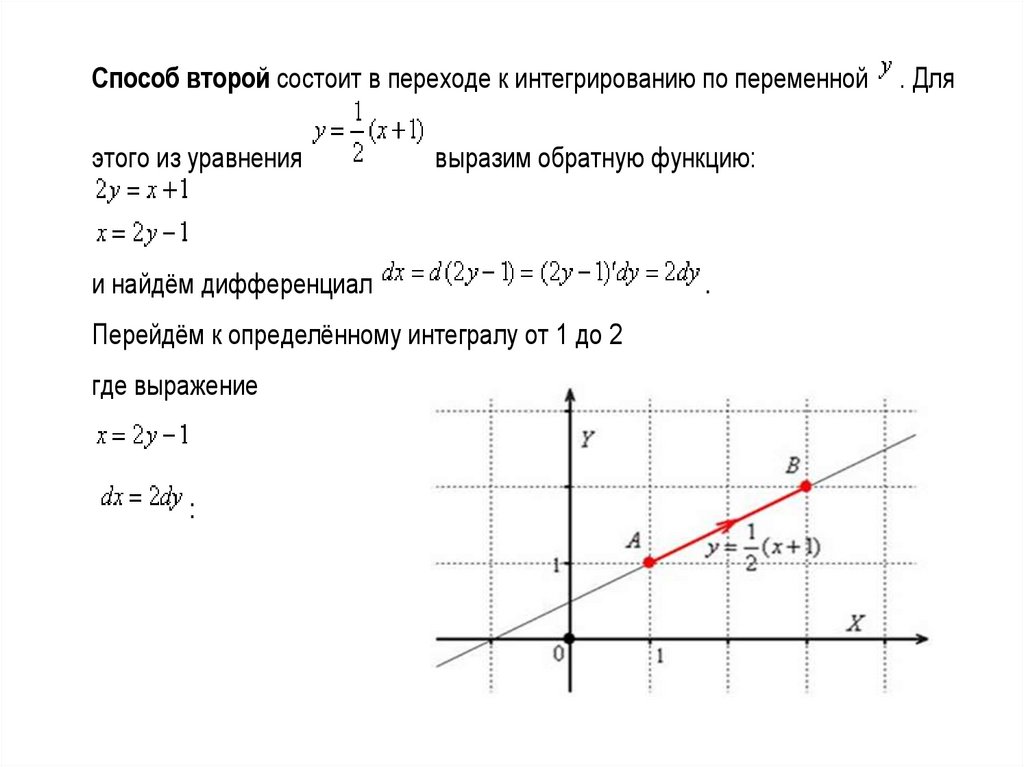
Способ второй состоит в переходе к интегрированию по переменнойэтого из уравнения
выразим обратную функцию:
и найдём дифференциал
Перейдём к определённому интегралу от 1 до 2
где выражение
:
.
. Для
18.
Ответ:19.
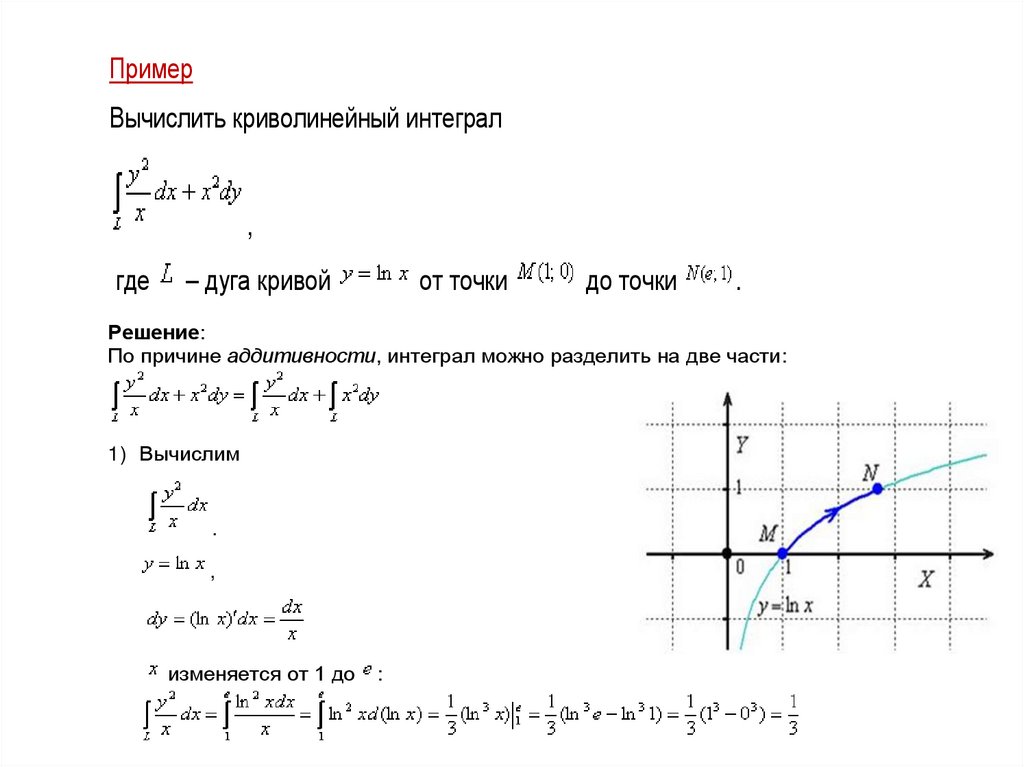
ПримерВычислить криволинейный интеграл
,
где
– дуга кривой
от точки
до точки
.
Решение:
По причине аддитивности, интеграл можно разделить на две части:
1) Вычислим
.
,
изменяется от 1 до
:
20.
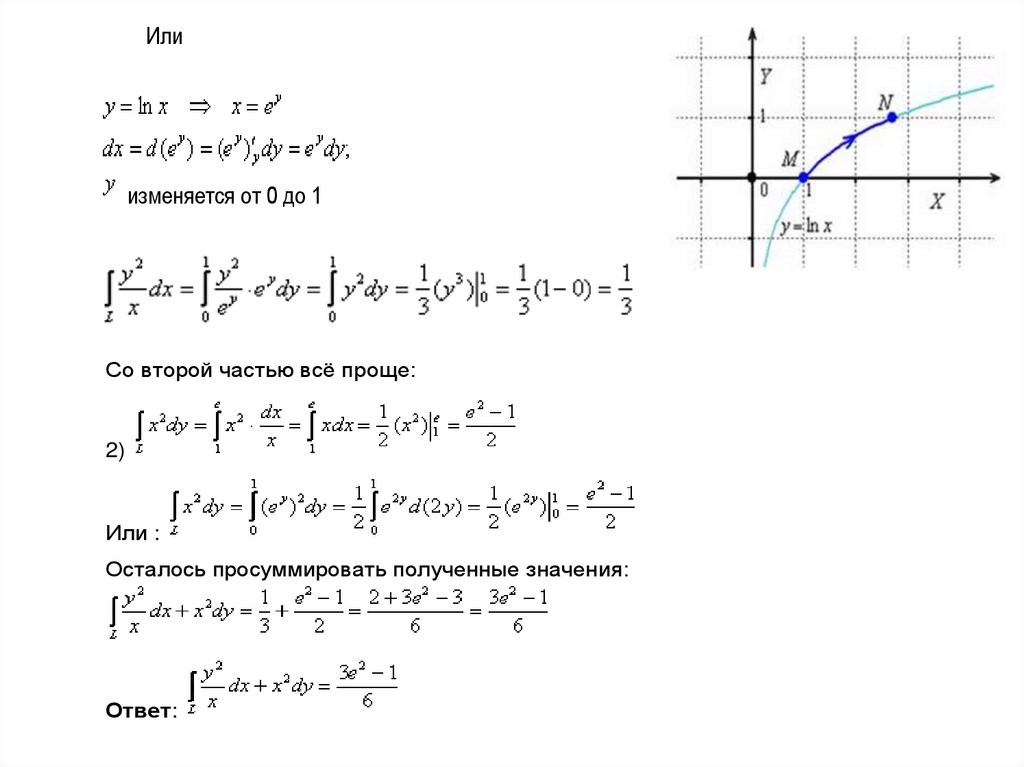
Илиизменяется от 0 до 1
Со второй частью всё проще:
2)
Или :
Осталось просуммировать полученные значения:
Ответ:
21.
ПримерВычислить криволинейный интеграл
по кривой
Решение:
в подынтегральном выражении нужно всё
выразить через параметр.
подставляем их в подынтегральное
выражение,
22.
Ответ:23.
Пример. Вычислить:x cos t; y sin t;
(
x
y
)
d
x
(
x
z
)
d
y
y
d
z
AB
:
z a t;0 t 2π
AB
2π
(cos t sin t ) ( sin t ) (cos t a t ) cos t sin t a dt
0
- cos t sin t sin
2π
2
t cos 2 t a t cos t a sin t dt
0
cos 2 t
2
2π
2π
2π
2π
0
0
0
cos 2tdt a t cos t dt a sin t dt
0
2π
cos 2 2π cos 2 0 1
2π
2π
sin 2t a(t sin t cos t ) 0 a cos t 0
2
2
2
0
1 1 1
1
sin 4π sin 0 a(2π sin 2π 0 cos 2π cos 0) a(cos 2π cos 0) 0.
2 2 2
2
Ответ: 0.





















 Математика
Математика








