Похожие презентации:
Кратные и криволинейные интегралы
1.
Математический анализ (2 семестр)Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
2020
2.
Кратные и криволинейные интегралыКриволинейный интеграл 1-го рода
y
z = f (x, y)
Аi
Mi
Аi+1
T - разбиение кривой AB:
A0= A, A1, A2 ,..., An=B
В
d (T ) max li
0 i n 1
А
x
n 1
n 1
i 0
i 0
n ( f ) f (M i ) li f ( xi , yi ) li
f ( xi , yi ) li
f ( x, y) dl d (lim
T ) 0
AB
Аналогичным образом определяется интеграл по пространственной кривой:
f ( xi , yi , zi ) li
f ( x, y, z) dl d (lim
T ) 0
AB
ВИТИ НИЯУ МИФИ, 2020
3.
Кратные и криволинейные интегралыСвойства криволинейного интеграла 1-го рода
1.
f (М ) dl f (М ) dl
AB
2.
ВА
L L1 L2 f ( M ) dl
L
3.
L2
L
f (M ) g (M ) dl f (M ) dl g (M ) dl
L
5.
L1
с f (M ) dl с f (M ) dl
L
4.
f (M ) dl f (M ) dl
L
L
dl L
L
6. M L : f ( M ) g ( M ) f ( M ) dl g ( M ) dl
L
7.
f (M ) dl
L
L
f ( M ) dl
L
ВИТИ НИЯУ МИФИ, 2020
4.
Кратные и криволинейные интегралыВычисление криволинейного интеграла 1-го рода
Если кривая AB задана параметрическим уравнением x = x(t) , y = y(t), z = z(t)
при α ≤ t ≤ β, где функции x(t), y(t), z(t) непрерывны, а x'(t), y'(y), z'(t)
непрерывны или кусочно-непрерывны, то справедливо равенство
f ( x, y, z ) dl f ( x(t ), y (t ), z (t )) ( x (t )) 2 ( y (t )) 2 ( z (t )) 2 dt
AB
Для плоской кривой:
f ( x, y ) dl f ( x(t ), y (t )) ( x (t )) 2 ( y (t )) 2 dt
AB
Если плоская кривая задана уравнением у = р ( х), a ≤ х ≤ b:
b
f ( x, y ) dl f ( x, p( x)) 1 ( p ( x)) 2 dx
AB
a
Для кривой L при полярной замене x ( ) cos , y ( ) sin , 0 1 :
AB
f ( x, y) dl
1
f ( ( ) sin cos , ( ) sin ) 2 ( ) ( ( )) 2 d
0
ВИТИ НИЯУ МИФИ, 2020
5.
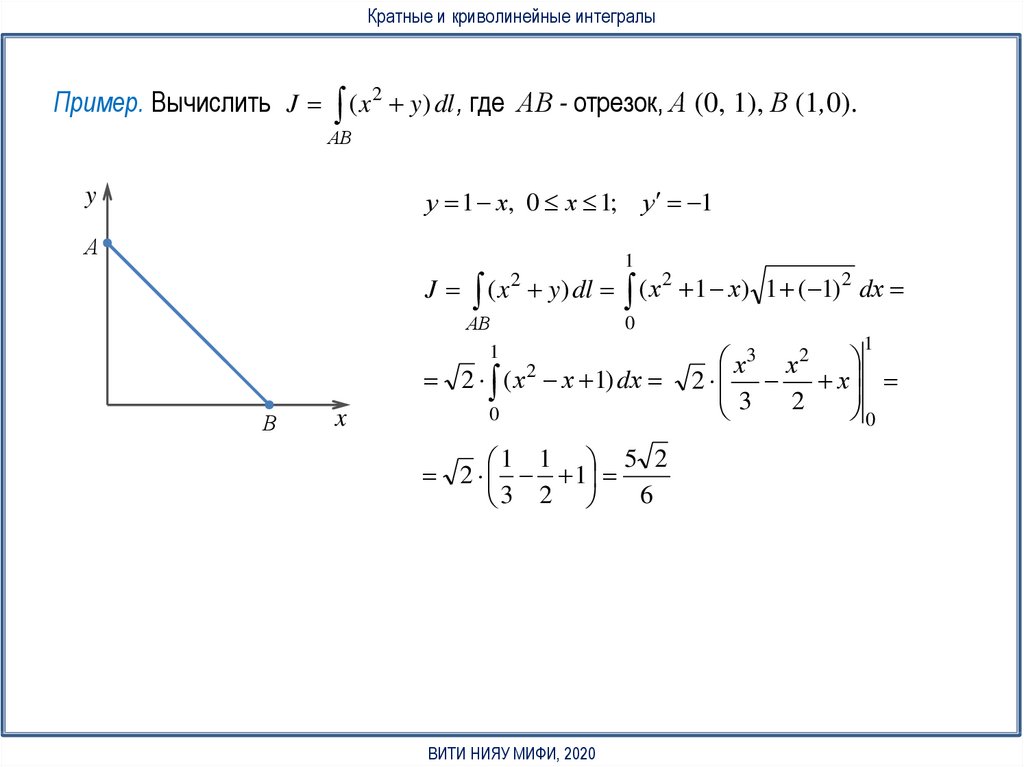
Кратные и криволинейные интегралыПример. Вычислить J ( x 2 y) dl , где АВ - отрезок, А (0, 1), В (1,0).
АВ
у 1
у 1 х, 0 х 1;
y
А
1
J
2
2
2
(
х
1
х
)
1
(
1
)
dх
(
x
y
)
dl
АВ
1
0
2 ( х 2 х 1) dх
В
x
0
1 1 5 2
2 1
6
3 2
ВИТИ НИЯУ МИФИ, 2020
1
х3 х 2
2
х
3
2
0
6.
Кратные и криволинейные интегралыПример. Вычислить J x 2 y 2 dl , где L – окружность х2 у 2 2х
L
х 2 у 2 2 х х 2 2 х у 2 0 х 2 2х 1 у 2 1 ( х 1)2 у 2 1
x cos , y sin
y
х 2 у 2 2 х ( cos )2 ( sin )2 2 cos
2 2 cos 2 cos ,
x
J x 2 y 2 dl
L
2
( ) ( ) ( ( )) d
2
2
2
2
2
2
2
2
L
2 cos (2 cos ) 2 ( 2 sin ) 2 d
8
ВИТИ НИЯУ МИФИ, 2020
2
( cos ) 2 ( sin ) 2 dl
2
2
4 cos d 4 sin
7.
Кратные и криволинейные интегралыПример. Вычислить J ( x y ) dl , где L - дуга циклоиды x t sin t , y 1 cos t
L
от точки А (0, 0) до В (2π ,0).
J ( x y ) dl
L
2
(t sin t 1 cos t ) (1 cos t ) 2 (sin t ) 2 dt
0
2
(t sin t 1 cos t )
2
1 2 cos t cos t sin t dt
2
2
0
2
(t sin t 1 cos t )
0
(t 2 sin( t 2) cos(t 2) 2 sin 2 (t 2)) 4 sin 2 (t 2) dt
0
2
2
(
t
2
sin(
t
2
)
cos(
t
2
)
2
sin
(t 2)) 2 sin( t 2) dt
0
2
2
2
0
0
0
2 t sin( t 2) dt 4 sin 2 (t 2) cos(t 2) dt 4 sin 3 (t 2) dt
8 z sin z dz 8 sin z cos z dz 8 sin 3 z dz 8
2
0
0
0
ВИТИ НИЯУ МИФИ, 2020
32
3
t 2z
dt 2dz
2 (1 cos t ) dt
8.
Кратные и криволинейные интегралыПример. Вычислить J z dl , где L – линия пересечения поверхностей
х у 1, z x
2
L
от точки А (0, 1, 0) до В (1, 0, 1)
1) Пусть х t у 1 t , z t 2 , 0 t 1
dl ( x (t )) 2 ( y (t )) 2 ( z (t )) 2 dt 12 ( 1) 2 (2t ) 2 dt
J
L
1
u 2 4t
2
32 6
6
1 u
1
z dl t 2 4t dt
u du
8 32
82
du 8t dt
0
2
2 4t 2 dt
2
63 2 23 2
3
1
12
2 3 2
2) Пусть z t x t , у 1 t , 0 t 1
2
2
1 1
dl
12 dt
2 t 2 t
J z dl
L
1
3 2
1
0
33 2 1
1 2t
t
dt
2t
1
0
1 1
1 2t
1 dt
dt
4t 4t
2t
1 2t
1
t
dt
2t
2
1
0
3
1
2 3 2
ВИТИ НИЯУ МИФИ, 2020
1 1 (1 2t )3 2
1 2t dt
32
2 2
1
0
9.
Кратные и криволинейные интегралыКриволинейный интеграл 2-го рода
Задача о нахождении работы плоского силового поля:
Пусть в каждой точке кривой KL определена некоторая переменная сила F ( x, y ) , и
под действием этой силы происходит перемещение точки по кривой KL от точки K
до точки L. Необходимо определить работу, которую при этом выполняет сила.
F (M i )
y
Ki
Mi
T - разбиение кривой KL:
K0= K, K1, K2 ,..., Kn=L
Ki+1
L
Ai ( F ( M i ), l i )
F ( x, y ) P( x, y ), Q( x, y )
K
l i xi , yi
( F ( M i ), l i ) P( xi , yi ) xi Q( xi , yi ) yi
x
A Ai ( F ( M i ), l i ) P( xi , yi ) xi Q( xi , yi ) yi
A lim
xi 0
yi 0
P( xi , yi ) xi Q( xi , yi ) yi
ВИТИ НИЯУ МИФИ, 2020
10.
Кратные и криволинейные интегралыПусть Ω – плоская область, в каждой точке которой задан вектор. Тогда говорят, что
в области Ω задано векторное поле.
Если выбрана декартова прямоугольная система координат, то векторное поле
можно задать при помощи двух скалярных функций:
F(x,y) = {P(x,y), Q(x,y)}.
Пусть кривая Г задана параметрическим уравнением x = x(t), y = y(t) при α ≤ t ≤ β.
Если движение по кривой осуществляется в направлении возрастания параметра t,
то кривая называется положительно ориентированной, в противном случае –
отрицательно ориентированной.
Криволинейный интеграл 2-го рода:
( F ( x, y), dl ) P( x, y) dx Q( x, y) dy lim
P( xi , yi ) xi Q( xi , yi ) yi
x 0
i
yi 0
Аналогичным образом определяется криволинейный интеграл 2-го рода для
трехмерного случая:
( F ( x, y, z ), dl ) P( x, y, z ) dx Q( x, y, z) dy R( x, y, z ) dz
ВИТИ НИЯУ МИФИ, 2020
11.
Кратные и криволинейные интегралыСвойства криволинейного интеграла 2-го рода
1. Криволинейный интеграл 2-го рода не зависит от способа параметризации
кривой.
2. Криволинейный интеграл 2-го рода при изменении ориентации кривой на
противоположную меняет знак:
( F (М ), dl ) ( F (М ), dl )
3. Аддитивность криволинейного интеграла 2-го рода относительно пути
интегрирования:
Г Г1 Г 2 ( F ( М ), dl ) ( F ( М ), dl ) ( F ( М ), dl )
Г
Г1
4. Связь криволинейных интегралов 1-го и 2-го рода:
Г2
( F ( x, y), dl ) P( x, y) cos Q( x, y) cos dl
ВИТИ НИЯУ МИФИ, 2020
12.
Кратные и криволинейные интегралыВычисление криволинейного интеграла 2-го рода
Если кривая Г задана параметрическим уравнением x = x(t), y = y(t) при α ≤ t ≤ β,
то dx x (t ) dt , dy y (t ) dt
P( x, y) dx Q( x, y) dy P( x(t ), y(t )) x (t ) Q( x(t ), y(t )) y (t ) dt
Если плоская кривая задана уравнением y = f (x), то t = x и
P( x, y) dx Q( x, y) dy P( x, f ( x)) Q( x, f ( x)) f ( x) dx
ВИТИ НИЯУ МИФИ, 2020
13.
Кратные и криволинейные интегралыПример. Вычислить интеграл
y dx х dy , где кривая Г задана параметрически в
виде х(t) = cos t, у(t) = sin t, 0 ≤ t ≤ π/2.
/2
/2
y dx х dy sin t (cos t ) cos t (sin t ) dt sin
2
/2
t cos t dt
2
0
0
0
Пример. Вычислить криволинейный интеграл 2-го рода
участок параболы у = х2 при 0 ≤ х ≤ 2.
2
у
х
2
2
xy dx х 2 dy х х х 2 ( х ) dx
0
2
2
0
dt / 2
xy dx
у
х
2
dy , где Г –
2
х4
16
3
2
х 2 х dx
х 4 8
4
0 4
ВИТИ НИЯУ МИФИ, 2020












 Математика
Математика








