Сумма бесконечной геометрической прогрессии

1. 18.05.20 Сумма бесконечной геометрической прогрессии при |q| < 1

18.05.20
Сумма бесконечной
геометрической прогрессии
при |q| < 1
1

2. " Прогрессия " – латинское слово, означающее "движение вперед", введено римским автором Боэцием (VIв) и понималось в более

" Прогрессия " – латинское слово,
означающее "движение вперед",
введено римским автором Боэцием (VIв) и
понималось в более широком смысле, как
бесконечная числовая последовательность
2

3. Что мы знаем о прогрессиях?

Мы выучили:
• определение, формулу п- ого
члена, суммы п - первых членов
арифметической и геометрической
прогрессий
3

4. "Сравнение – сопоставление объектов с целью выявления черт сходства и черт различия между ними " (Философский словарь)

"Сравнение –
сопоставление объектов с
целью выявления черт
сходства и черт различия
между ними "
(Философский словарь)
4

5.

"Сравнение есть основа
всякого понимания и всякого
мышления . . . "
(К.Д. Ушинский)
5

6.

Арифметическая
прогрессия
Геометрическая
прогрессия
(bn) –
(an ) – арифметическая
прогрессия
an+1=an+d
d - разность арифметической
прогрессии
геометрическая
прогрессия
bn+1 = bn·q
q – знаменатель геометрической
прогрессии
Формула n- ого члена
an =a1 + d·(n – 1)
bn=b1·qn-1
Формула сумма n - первых членов
a1 an
Sn
n
2
S
n
2a1 d ( n 1 )
n
2
b1 q n 1
sn
q 1
bn q b1
sn
q 1
6

7. Упражнения (1)

1) Представить в виде десятичной
периодической дроби обыкновенную
дробь
в) 7
а) 1 ;
б)
5
1
.
12
11
3
ответы:
а)
0,333…=0,(3);
б)
0,4545…= 0,(45);
в)
1,58333…= 1,58(3)
7

8.

2) Представьте данное число сначала в
виде а0, а1 а2 а3 . . . , а затем в виде
суммы по образцу:
3
3
3
2,8 3 2,8333 ... 2,8
...
100 1000 10000
а) 1,(7);
б) 3,2(5);
в) -0,81(36)
ответы:
а) 1,(7) = 1,777… = 1
б)
7
7
7
...
10 100 1000
5
5
5
...
3,2(5) = 3,2555… = 3,2 +
100 1000 10000
в) -0,81(36) = -0,813636… = 0,81
28.01.2008 г
36
36
...
10000 1000000
грязнова А.К.
Упражнения (2)
8

9. Каким образом сумма бесконечного числа слагаемых может быть конечным, вполне определенным числом?

9

10. Главная проблема

• Почему Ахиллес никогда не догонит
впереди идущую черепаху?
10

11. Один из "парадоксов Зенона"

Один из "парадоксов
Зенона"
(древнегреческого философа) состоит в следующем (в
изложении Льва Толстого в "Войне и мире", т. 3, ч. 3).
Ахиллес никогда не догонит впереди идущую
черепаху, несмотря на то, что Ахиллес идет в десять
раз скорее черепахи: как только Ахиллес пройдет
пространство, отделяющее его от черепахи,
черепаха пройдет впереди его одну десятую этого
пространства; Ахиллес пройдет эту десятую,
черепаха пройдет одну сотую и т.д. до
бесконечности.
11

12.

Один из "парадоксов Зенона“ (2)
• Задача представлялась древним
неразрешимой (она и в настоящее время не
считается полностью решенной). Отрезки,
последовательно пробегаемые
Ахиллесом, составляют
геометрическую прогрессию со
знаменателем 0,1.
12

13.

1
1
1
1
...
10
100
1000
(за единицу принимаем начальное
расстояние между Ахиллесом и
черепахой). Общее расстояние,
пройденное Ахиллесом до встречи с
черепахой, есть
"сумма бесконечного числа членов":
13

14.

• Обозначим сумму через S:
S 1
1
1
1
...
10 100 1000
1
1
1
10 S 10 1
. . . 10 S ,
10 100 1000
10 S - S 10 ,
S
10 1
1
9 9
Так учил Л.Н.Толстой в Яснополянской школе детей
переводить бесконечные десятичные дроби в
обыкновенные
14

15. Изучение нового (1)

1; 1 ; 1 ; 1 ; … — бесконечная геометрическая
1).
2 4 8
прогрессия
1
1
• b1 = 1; b2= ; q = , |q| < 1
2
2
b1 q n 1
n
q 1
s
n
n
1
1
1
1
n
1
1
2
2
2 2 2
n 1
n 1
1
2
2
1
2
2
s
n 1
;
При n , 2
sn 2 ,
1
2
n 1
0.
s 2 , где S - сумма бесконечной геометрической
прогрессии при q 1.
15

16. Сумма бесконечной геометрической прогрессии S = b1 при |q| < 1 1- q

b1 ; b2 ; b3 …— убывающая
геометрическая прогрессия |q| < 1
sn s при n ,
2)
b1 q n 1
b1 q n b1
b1 b1 q n
b1
b1 q n
т.к. sn
.
q 1
q 1
1 q
1 q
1 q
b1
n
При n , q 0 , S n
.
1 q
Сумма бесконечной геометрической
прогрессии
S = b1
при |q| < 1
1- q
грязнова А.К.Изучение
нового(2)
16

17. Первичное закрепление

• Представить бесконечную десятичную
периодическую дробь 1,(7) в виде
обыкновенной дроби
Решение
а) 1,(7) = 1,777… = 1
7
7
7
;
;
; ...
10 100 1000
S
b1
при q 1
1 q
7 7
7
...
10 100 1000
геометрическая прогрессия b = 7 ; b = 7
1
2
10
100
1
q = 10 , |q| < 1
7
7
7
S 10 10
9
9
1 1
10 10
Тогда 1,(7) = 1+
7
7
=1
9
9
17

18. Первичное закрепление

• Представить бесконечную десятичную
периодическую дробь 0,(18) в виде
обыкновенной дроби
Решение
0,(18) =0, 181818. . . = 0,18 + 0,0018 + 0,000018 + . . . = ?
0,18, 0,0018, 0,000018, . . . - геометрическая прогрессия
b1 =0,18; b2 =0,0018; q =0,01, |q| < 1
S
b1
при q 1
1 q
S=
0,18
0,18 18
2
1 0,01 0,99 99 11
Тогда 0,(18) =
2
11
18

19. Что же нового узнали мы?

Познакомились с понятиями
бесконечной геометрической прогрессии;
суммы бесконечной геометрической
прогрессии;
С формулой суммы бесконечной
геометрической прогрессии и её применением
Учились заменять бесконечные периодические
дроби обыкновенными
19

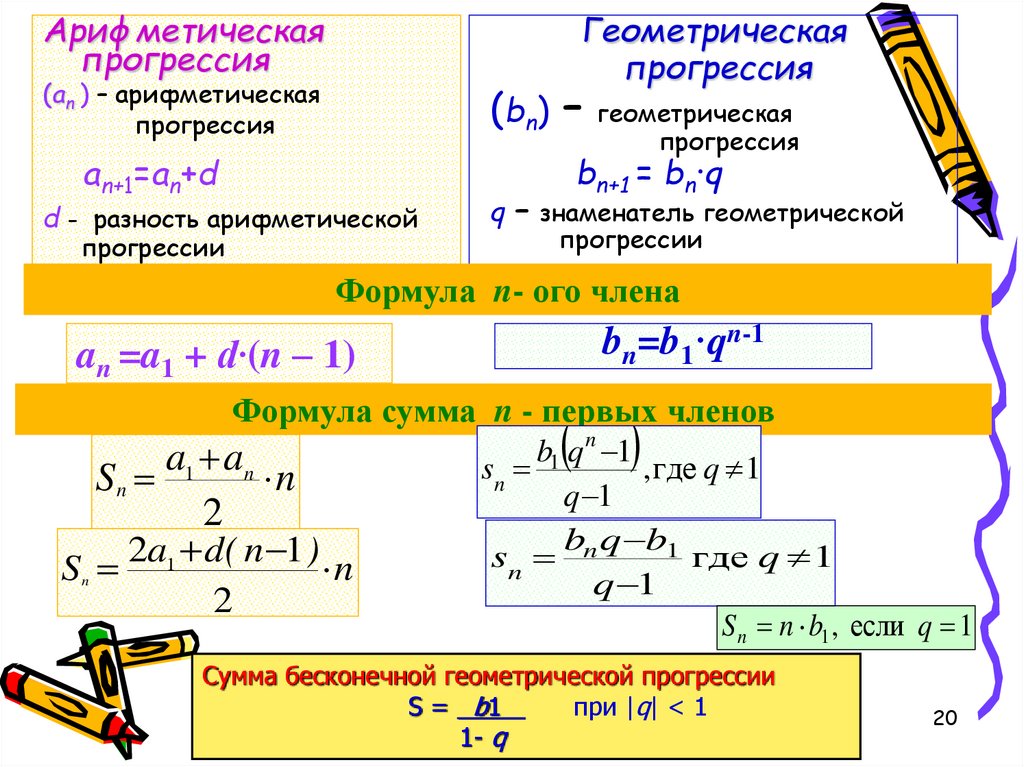
20.

Арифметическая
прогрессия
Геометрическая
прогрессия
(bn) –
(an ) – арифметическая
прогрессия
an+1=an+d
d - разность арифметической
прогрессии
геометрическая
прогрессия
bn+1 = bn·q
q – знаменатель геометрической
прогрессии
Формула n- ого члена
bn=b1·qn-1
an =a1 + d·(n – 1)
Формула сумма n - первых членов
a1 an
Sn
n
2
S
n
2a1 d ( n 1 )
n
2
b1 q n 1
sn
, где q 1
q 1
b q b1
sn n
где q 1
q 1
S n n b1 , если q 1
Сумма бесконечной геометрической прогрессии
S = b1
при |q| < 1
1- q
20

21. Словарь терминов

Перечислите и определите термины,
используемые в теме прогрессии
Числовая последовательность
Арифметическая прогрессия
Разность арифметической прогрессии
Геометрическая прогрессия
Бесконечная геометрическая прогрессия
Знаменатель геометрической прогрессии
Формула n-ого члена
Рекуррентная формула
Формула суммы n-первых членов
последовательности
21

22. Ответьте на вопросы:

• 1) По какому плану сравнивали изученные
понятия "Арифметическая и геометрическая
прогрессии«?
• 2) Укажите их общие существенные признаки.
• 3) Определите существенные различия между
ними.
• 4) Сделайте вывод, вытекающий из сравнения.
22