Статистикалық болжамдарды тексеру теориясы негіздері

1. ДӘРІС Статистикалық болжамдарды тексеру теориясы негіздері

2.

Медициналық зерттеулерде ағза
көрсеткіштерін салыстыру (үрдісі)
процесі маңызды орын алады:
• Қалыпты және патология
• Емге дейін және кейін
• Әртүрлі емдеу тәсілдерін салыстыру
және т.б.

3. Сонымен бірге бізді генералды жиынтық қызықтырады бірақ бізге қол жетімдісі ережедегідей таңдамалы берілгендер

4.

• Алайда, таңдамалы зерттеу нәтижесін
әрқашанда барлық генералды
жиынтыққа тарату мүмкін бола бермейді

5.

• Сондықтан алдын ала статистикалық
болжамдар(жорамал) жасау ұсынылады

6.

Генералды
жиынтық 1
Генералды
жиынтық 2
Генералды
жиынтық
таңдама 1
Таңдама 2
таңдама 1
таңдама 2

7.

Басқа болжамдар мысалы:
• Орташаның қандай да нақты санға теңдігі
туралы
• Екі дисперсияның теңдігі туралы
• Кездейсоқ шаманың тарамдалу түрі туралы
• Екі кездейсоқ шаманың арасындағы
байланыстың бар болуы туралы

8.

Статистикада нөлдік және альтернативті
болжамдар ерекшеленеді:
Нөлдік болжамН(0) – бұл болжам
• теңдік туралы(қандай да бір әрекеттің тиімділігі
теріске шығарылады),
• сәйкестік туралы,
• тәуелсіздігі туралы(қандай да бір фактордан)
• егер нөлдік болжам расталмаса, онда
альтернативті болжам қабылданады Н(1)

9.

• Болжамдардың ішінен қайсысы
қызығушылық тудырады?

10.

• Болжамдар генералды жиынтыққа
байланысты тұжырымдалады,
Ал шешімі тәжірибе(зерттеу) нәтижесінде
алынған таңдамалы берілгендер
бойынша қабылданады.

11.

Сондықтан қате жіберу мүмкіндігі
(ықтималдығы) бар.
Н(0) дұрыс бола тұра біз оны теріске
шығара отырып жіберетін максималды
қате, белгіленуі α (альфа) болатын
мәнділік деңгейі деп аталады

12.

• Мәнділік деңгей– бұл альтернативті
болжамды қабылдай отырып, өзіміз
жіберетін шектік қате.

13.

• α мәнділік деңгейі шешілетін мәселенің мәніне
негізделіп, зерттеушінің өзімен беріледі. Медикобиологиялық есептерде әдетте α =0,05 (5%) немесе
0,01( 1 %) деп алынады.
• егер α =0,05 кезінде біз альтернативті болжамды
қабылдасақ, онда неғұрлым 95% жоғары жағдайда
болжам дұрыс, ал неғұрлым 5% төмен болса- қате.

14.

• Болжамды қабылдау немесе теріске
шығару үшін критерий қолданылады

15.

Болжамдарды тексеру үшін критерийлердің 2 түрі:
• параметрлік (қалыпты тарамдалған заң бойынша
сандық кездейсоқ шама үшін және n>30)
• Параметрлік емес
Егер белгілер сандық болса, бірақ тарамдалу
қалыптыға сәйкес келмесе немесе белгісіз және
тексеруге болмаса (яғни n<30)
Немесе егер белгілер сапалық болса

16.

Таңдама критерийі анықталады, сол
сияқты салыстырылатын таңдамалар
тәуелді немесе тәуелсіз бола ала ма?
• Тәуелсіз таңдамалар– бұл таңдама,
әртүрлі объектілерден құралған,
сонымен бірге бір таңдамадаңы
кездейсоқ шама мәні басқа таңдамадағы
оның мәндеріне тәуелді емес.
• Тәуелді таңдамалар «дейін» және
«кейін» зерттелген бір және сол
объектілерден тұрады,

17.

• Болжамды екі жолмен тексеруге
болады
I алгоритм
• Н(0) және Н(1) жасау
• α мәнділік деңгейін таңдау
• болжамды тексеру үшін статистикалық
критерийді таңдау

18.

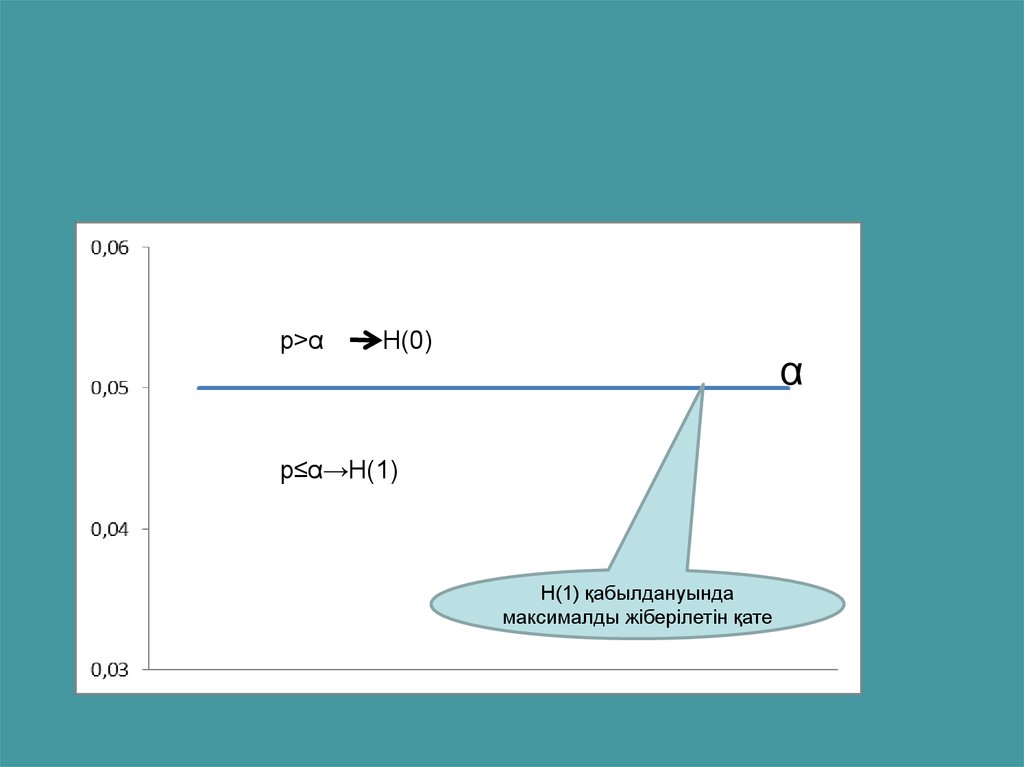
• Әрі қарай таңдамалық берілгендер негізінде
біз қандай р қате жіберетініміз анықталады,
егер нөлдік болжамды теріске шығарсақ,
яғни мәнділік денгейіне жеткен- Н(1)
қабылдаймыз
• Егер р ≤ α онда альтернативті болжам
қабылданады (нөлдік теріске шығарылады)
• Ал, егер р > α, онда нөлдік болжам
қабылданады
р компьютерлік бағдарламалармен
анықтауға мүмкіндік бар

19.

p>α
H(0)
α
p≤α→H(1)
Н(1) қабылдануында
максималды жіберілетін қате

20. II алгоритм

• α мәнділік деңгейін таңдау
• нөлдік және альтернативті болжамдарды жасау
• болжамды тексеру үшін статистикалық
критерийді таңдау
• критерийдің мәнін есептеу
• берілген мәнділік деңгей үшін оның критикалық
мәнімен есептелген мәнін салыстыру
• Ккритикалық мәнді берілген мәнділік деңгейде
арнайы кесте бойынша табамыз
• есептелегн және критикалық мәнді салыстыру
негізінде Н(0) немесе Н(1) қабылданады

21. Екі генералды орташаның теңдігі туралы болжамды тексеру үшін Стьюдент параметрлік криетрийін қолдану

• Сипаттамаларымен екі таңдама бар болсын
Сол сияқты Dген1 =
Dген2 белгілі

22.

Генералды жиынтық1
X
ген 1
таңдама 1
X тан1 m1
Генералды жиынтық2
X
ген 2
таңдама 2
X тан2 m2

23.

Екі генералды орташаның теңдігі туралы
нөлдік болжамды тексереміз ( яғни екі
таңдама бір генералды жиынтықтан
алынғаны туралы)

24.

Жағдай 1. таңдамалар тәуелсіз
• α мәнділік деңгейін береміз
• Болжамдарды тексеру үшін параметрлік tСтъюдент критерийін қолданамыз
Оның мәнін есептейміз:
tecen
X1 X 2
m m
2
1
2
2

25.

α мәнділік деңгейіне сәйкес және бостандық
дәрежесі саны бойынша кесте бойынша
f n1 n2 2
tкрит
табамыз
егер │ tесеп │< tкрит онда
X ген1 X ген 2
Егер │ tесеп│≥ tкрит онда
X ген1 X ген 2

26.

Генеральды жиынтық
X
Таңдама 1
X тан1 m1
ген
Таңдама 2
X тан2 m2

27.

• Жағдай 2. Таңдамалар тәуелді
Бұған ұқсас зерттеулер кезінде барлық бақылауды
n-жұп өлшемді түріне келтіруге болады (мысалы,
дейін және кейін)
Әрбір жұп үшін айырма есептеледі
di,
i=1, n
Алынған қатар үшін орташа есептеледі
sd
Және орташа квадраттық ауытқу
мәнін есептейміз
d
t
sd / n
d

28.

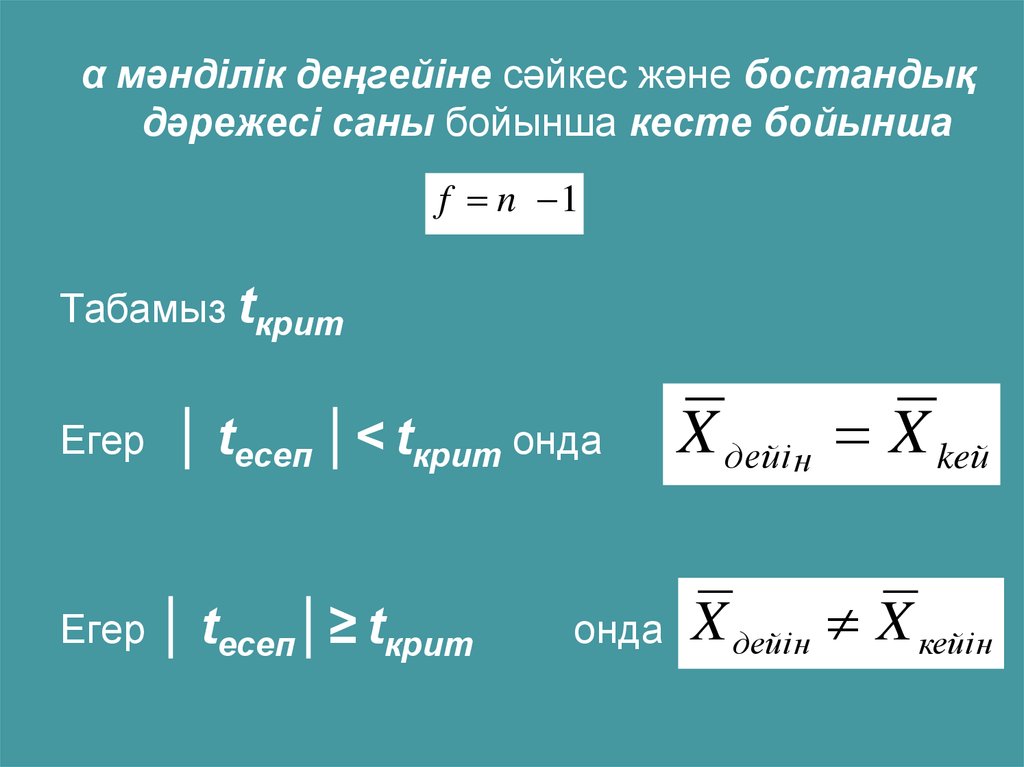
α мәнділік деңгейіне сәйкес және бостандық
дәрежесі саны бойынша кесте бойынша
f n 1
Табамыз tкрит
Егер
│ tесеп │< tкрит онда
Егер │ tесеп│≥ tкрит
онда
X дeйi н X keй
X дейiн X кейiн

29.

t критикалық мәні (екіжақтылық нұсқасы)
α мәнділік деңгейі
f
0,50
0,20
0,10
0,05
1
1,000
3,078
6,314
12,706
2
0,816
1,886
2,920
3
0,765
1,638
4
0,741
5
0,02
0,01
0,005
0,002
0,001
31,821
63,657
127,321
318,309
636,619
4,303
6,965
9,925
14,089
22,327
31,599
2,353
3,182
4,541
5,841
7,453
10,215
12,924
1,533
2,132
2,776
3,747
4,604
5,598
7,173
8,610
0,727
1,476
2,015
2,571
3,365
4,032
4,773
5,893
6,869
6
0,718
1,440
1,943
2,447
3,143
3,707
4,317
5,208
5,959
7
0,711
1,415
1,895
2,365
2,998
3,499
4,029
4,785
5,408
8
0,706
1,397
1,860
2,306
2,896
3,355
3,833
4,501
5,041
9
0,703
1,383
1,833
2,262
2,821
3,250
3,690
4,297
4,781
10
0,700
1,372
1,812
2,228
2,764
3,169
3,581
4,144
4,587