Похожие презентации:
Скалярное произведение векторов. Угол между векторами
1.
Скалярноепроизведение векторов.
Угол между векторами.
2.
ОпределениеСкалярным произведением двух
векторов называется произведение
их длин на косинус угла между ними.
a b = a b cos(a b )
Скалярное произведение векторов – число
(скаляр).
3.
Формула для нахожденияскалярного произведения
через координаты векторов
a = x1 i + y1 j + z 1 k
a b= ?
b = x2 i + y2 j + z 2 k
a b= (x1 i + y1 j + z1 k) (x2 i + y2 j + z2 k) =
= x1x2 + y1y2 + z1z2
a b = x1x2 + y1y2 + z1z2
4.
Пример №1Найти скалярное произведение векторов:
a {-6; 9; 5}
b {-1; 0; 7}
a b= x1x2 + y1y2 + z1z2
a b= -6 (-1) + 9 0 + 5 7 = 41
5.
Пример №2Найти скалярное произведение векторов:
a {0; 0; 4}
b {22; 1; 8}
a b= x1x2 + y1y2 + z1z2
a b= 0 22 + 0 1 + 4 8 = 32
6.
Пример №3Найти скалярное произведение векторов:
a {1; 7; 9}
b {-2; 4; 0}
a b= x1x2 + y1y2 + z1z2
a b = 1 (-2) + 7 4 + 9 0 = 26
7. Косинус угла между векторами
cosа 2; 2;0
с 3;0; 3
a b
a b
cos
xa xb ya yb za zb
xa2 ya2 za2 xb2 yb2 zb2
2 3 2 0 0 3
2 2 0 3 0 3
2
2
2
2
2
2
6 0 0
6
4 4 0 9 0 9
8 18
6
6
6 1
4 2 2 9 4 3 12 2
1
Ответ : 60
cos 60
2
8.
СА х А хС ; у А уС ; А СДано : А 1;3;0
СА 1 1;3 2;0 1 0;1;1
В 2;3; 1 , С 1;2; 1
Найти : СА; СВ
cos
cos СА; СВ
СВ хВ хС ; уВ уС ; В С
a b
a b
СВ 2 1;3 2; 1 1 1;1;0
xa xb ya yb za zb
xa2 ya2 za2 xb2 yb2 zb2
0 1 1 1 1 0
0 1 1 1 1 0
2
2
2
2
2
2
1
1
2 2 2
1
cos СА; СВ СА;СВ 60
2
Ответ : СА; СВ 60
9.
Дано: А 3; 2;4 В 4; 1;2С 6; 3;2 D 7; 3;1
Найти: угол между прямыми АВ и CD.
Ваши предложения…
1. Найдем координаты векторов АВ 1;1; 2 и
CD 1;0; 1
2. Воспользуемся формулой:
cos
cos
x1 x2 y1 y 2 z1 z 2
x y z x y z
2
1
1 1 1 0 2 1
2
1
2
1
12 12 2 12 0 2 1
2
3
cos
2
2
2
2
2
2
2
2
3
3
3
3
6 2
12 2 3 2
φ = 300
10.
Проверочная работа1.Найти скалярное произведение векторов:
А)
Б)
a {1; 10; 7} b {0; 7; 0}
a {7; 25; 0}
В) a {-1; 2; 8}
2.
b {11; 0; 54}
b {5; 5; 0}







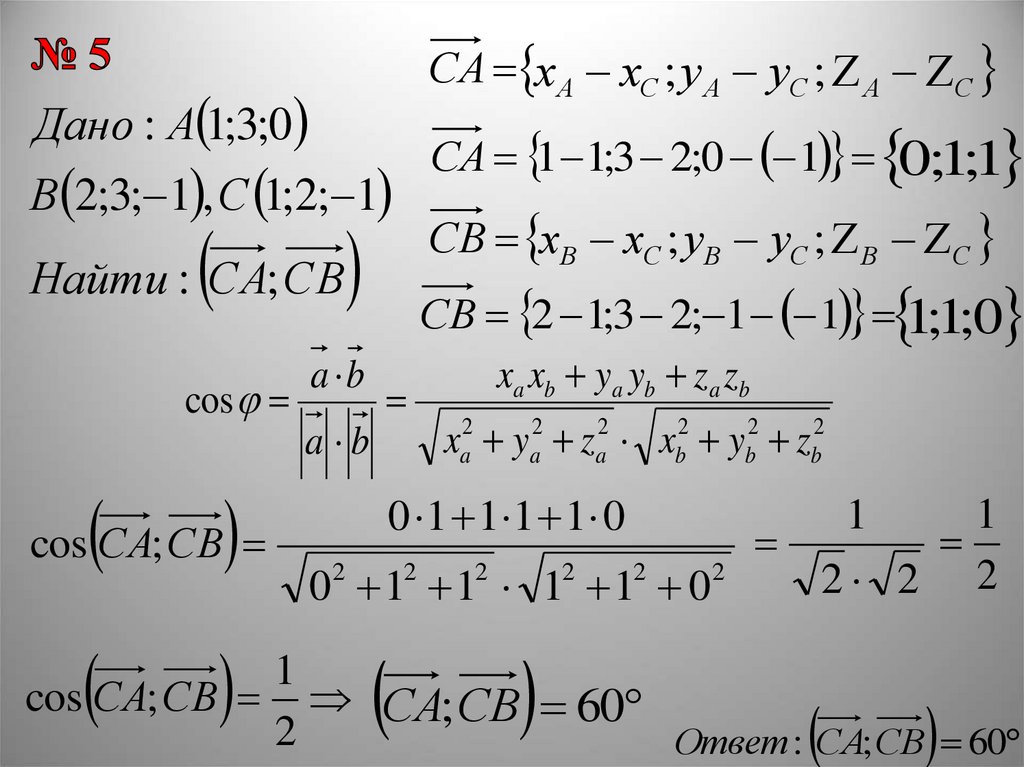


 Математика
Математика