Похожие презентации:
Скалярное произведение векторов
1.
Скалярноепроизведение векторов
2. Повторяем теорию:
• Как находят координаты вектора, если известныкоординаты его начала и конца?
АВ хВ х А ; уВ у А ; z B z A
• Как находят координаты середины отрезка?
х А хВ
;
2
• Как находят длину вектора?
у А уВ
;
2
z A zB
2
а х2 у2 z 2
• Как находят расстояние между точками?
АВ
х
х А у В у А z B z A
2
В
2
• Как вы понимаете выражение «угол между
векторами»?
2
3.
Решить задачи.; 2;4 В 4;3;2
1) Дано: А 3
30
Найти: АВ
; 5;0 С 5;0; 4 D 7; 2; 3
; 3;1 В 4
2) Дано: А 2
Равны ли векторы АВ и CD ?
Нет, т.к.равные векторы имеют равные
координаты.
2; 2; 1
АВ
2
CD
; 2;1
3) Дано: ? Коллинеарны ли векторы АВ и CD ?
А 1
; 3;4
В 9;1; 2
С 2;0;1
D 4
; 2;2
8;4; 6 CD
АВ
2
; 2;1
Нет
4.
Угол между векторамиb
О
a
Угол между векторами
равен .
a b =
a
и
b
5.
Угол между векторами.b
ОА а ОВ b
ab
а
Если а b, то
0
Если а b то ab 180
А
0
α
О
аb 0
В
то ab 90
Если а b
0
6.
Найдите угол между векторамиa b = 300
a
a c = 1200
d
300
c
b
f
b c = 900
d c = 1800
d f = 00
7.
ОпределениеСкалярным произведением двух
векторов называется произведение
их длин на косинус угла между ними.
a b = a b cos(a b )
Скалярное произведение векторов – число
(скаляр).
8.
Вспомним планиметрию…a
b a b cos
Если a
b , то
cos90 0 a b 0
0
0
a
b
Если
, то cos
a b a b
180 1
a b a b
cos0 1
Если
а b
Если
b
a
a
a
a
a
a
a b , то a
Скалярное произведение a a называется
, то
0
скалярным квадратом вектора
2
2
9.
Частный случай №1b
a b = 900
a
a b =
=0
a b cos 900 = 0
Скалярное произведение ненулевых
векторов равно нулю тогда и только тогда,
когда эти векторы перпендикулярны.
a b = 0
a b
10.
Частный случай №2a b < 900
b
a
a b =
>0
a b cos > 0
Скалярное произведение ненулевых векторов
положительно тогда и только тогда, когда угол
между векторами острый.
a b > 0 a b < 900
11.
Частный случай №3b
a b > 900
a
a b =
<0
a b cos < 0
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда, когда угол
между векторами тупой.
a b < 0 a b > 900
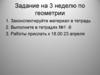
12.
Частный случай №4b
a b = 00
a
a b =
1
a b cos 00 = a b
b
a b = 1800
a
a b =
-1
a b cos1800 = – a b
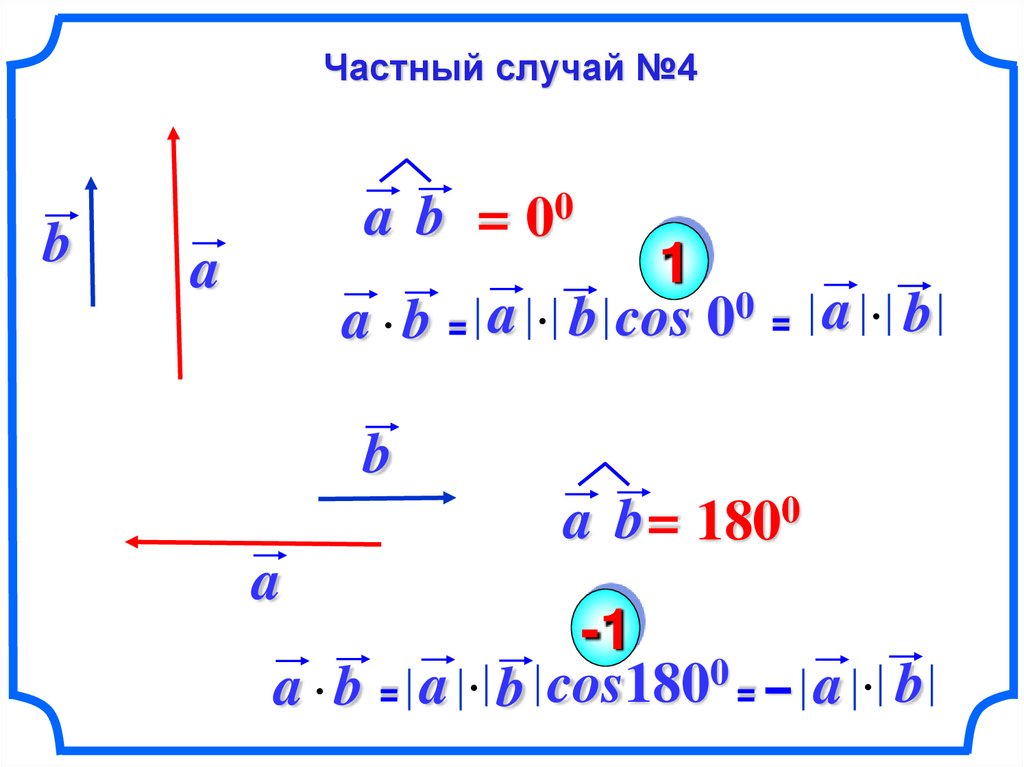
13.
Частный случай №5a a = 00
a
a a =
1
a a cos 00 = a a
Скалярное произведение
a a
скалярным квадратом вектора
=
a
называется
a
и обозначается
a
2
2
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
a
2
=
a
2
14. Визуальный разбор задач из учебника (п.48).
№1. Найти угол между двумя прямыми(пересекающимися или скрещивающимися), если
известны координаты направляющих векторов этих
прямых.
q x ; y ; z
p x ; y ;z
а)
р
1
1
1
б)
2
2
2
р
q
р
р
θ
q
q
q
θ
φ=θ
φ = 1800 - θ
15. Визуальный разбор задач из учебника (п.48).
№2. Найти угол между прямой и плоскостью, еслиизвестны координаты направляющего вектора
прямой и координаты ненулевого вектора,
перпендикулярного к плоскости..
p x1; y1; z1
а)
б)
п x2 ; y2 ; z2
п
θ
п
а
θ
р
φ
р
φ
α
α
а
φ
16.
Формула скалярного произведениявекторов в пространстве.
а x1;y1;z1
b x2;y2;z2
a
b
x
x
y
y
z
z
12
12
12
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
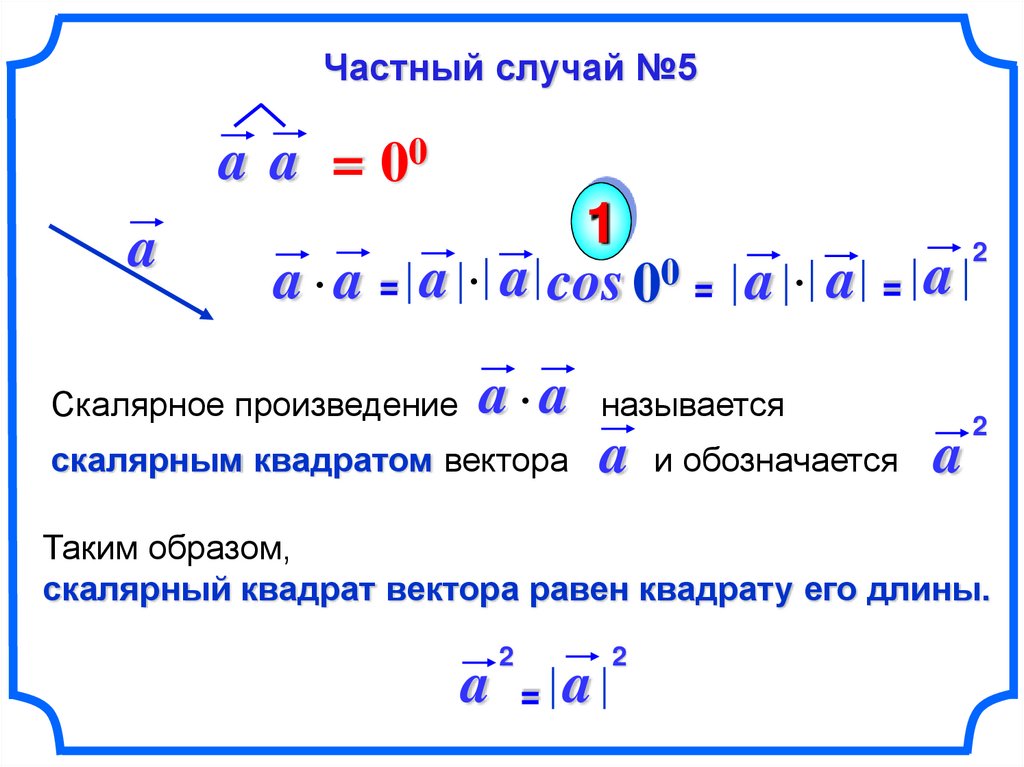
17.
Решение задач.Дан куб АВСDA1B1C1D1.
Найдите угол между векторами:
B1
В1 В и В1С
450
б) ВС и АС
450
а)
в) DA
и B1 D1
C1
A1
D1
B
1350
A
C
D
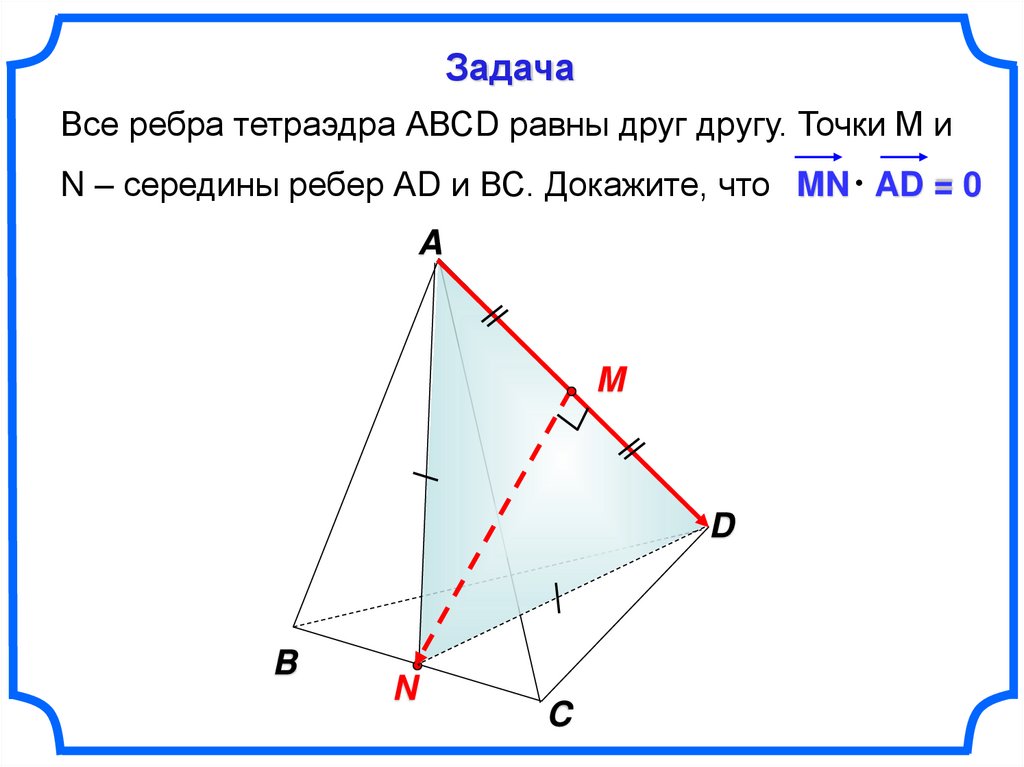
18.
ЗадачаВсе ребра тетраэдра АВСD равны друг другу. Точки М и
N – середины ребер АD и ВС. Докажите, что MN AD = 0
A
M
D
B
N
C
19.
Формула для нахожденияскалярного произведения
через координаты векторов
a = x1 i + y1 j + z 1 k
a b= ?
b = x2 i + y2 j + z 2 k
a b= (x1 i + y1 j + z1 k) (x2 i + y2 j + z2 k) =
= x1x2 + y1y2 + z1z2
a b = x1x2 + y1y2 + z1z2
20.
Пример №1Найти скалярное произведение векторов:
a {-6; 9; 5}
b {-1; 0; 7}
a b= x1x2 + y1y2 + z1z2
a b= -6 (-1) + 9 0 + 5 7 = 41
21.
Пример №2Найти скалярное произведение векторов:
a {0; 0; 4}
b {22; 1; 8}
a b= x1x2 + y1y2 + z1z2
a b= 0 22 + 0 1 + 4 8 = 32
22.
Пример №3Найти скалярное произведение векторов:
a {1; 7; 9}
b {-2; 4; 0}
a b= x1x2 + y1y2 + z1z2
a b = 1 (-2) + 7 4 + 9 0 = 26
23. Направляющий вектор прямой.
аВ
А
• Ненулевой вектор называется
направляющим вектором
прямой, если он лежит на
самой прямой, либо на прямой,
параллельной ей.
24. № 464 (а)
Дано: А 3; 2;4 В 4; 1;2 С 6; 3;2 D 7; 3;1Найти: угол между прямыми АВ и CD.
Ваши предложения…
1. Найдем координаты векторов
АВ 1;1; 2 и CD 1;0; 1
2. Воспользуемся формулой:
cos
x1 x2 y1 y 2 z1 z 2
x y z x y z
2
1
2
1
2
1
2
2
φ = 300
2
2
2
2
25.
№ 466 (а)Дано: куб АВСDA1B1C1D1
точка М принадлежит АА1
АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прям. MN и DD1
z
1. Введем систему координат.
D1
2. Рассмотрим DD1 и МN.
A1
3. Пусть АА1= 4, тогда
М 0;4;3
N 4;2;0
4. Найдем координаты
векторов DD1 и MN.
5. По формуле найдем cosφ.
3
Ответ: 29
C
1
B1
М
D
A
у
C
B
N
х
26.
Задача.Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; DA = 2; DC = 2; DD1 = 3.
Найти угол между прямыми СВ1 и D1B.
Ваши предложения…
1. Введем систему координат Dxyz
2. Рассмотрим направляющие A1
прямых D1B и CB1.
CВ1 1;0;3
D1 B 1;2; 3
z
D1
C
1
B1
3
3. По формуле найдем cosφ.
4
cos
35
47 0 28 '
1
х
A
D
2
C
B
у
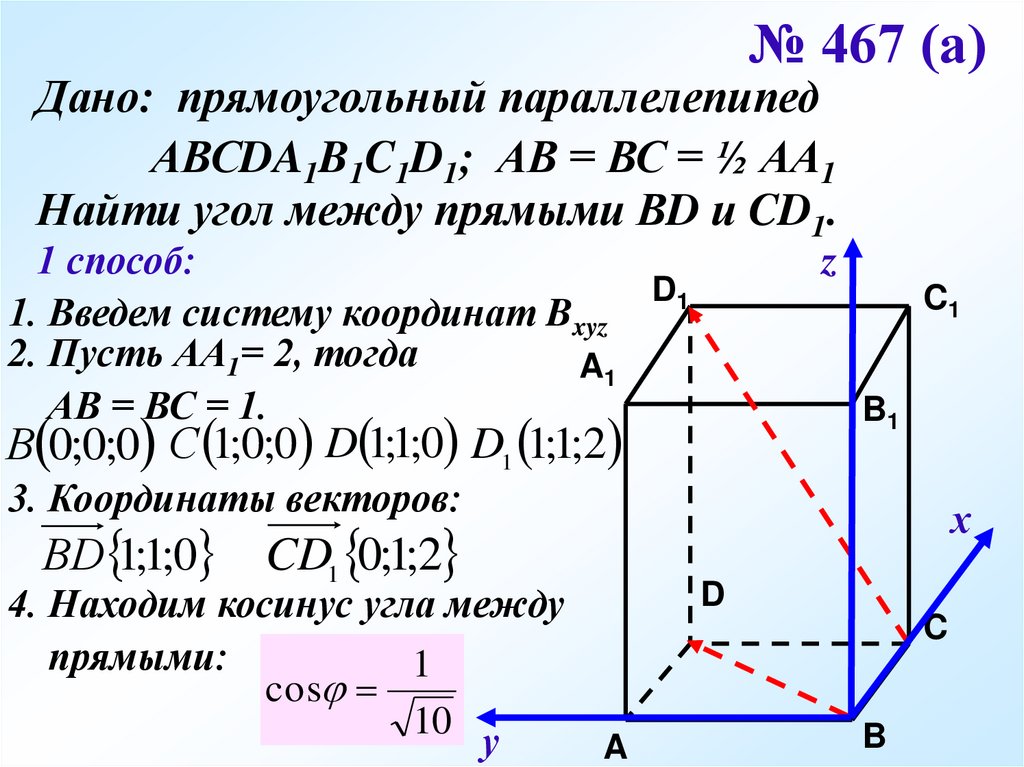
27.
№ 467 (а)Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
1 способ:
D1
1. Введем систему координат Bxyz
2. Пусть АА1= 2, тогда
A1
АВ = ВС = 1.
z
C1
B1
В 0;0;0 С 1;0;0 D 1;1;0 D1 1;1;2
3. Координаты векторов:
ВD 1;1;0
CD1 0;1;2
4. Находим косинус угла между
прямыми:
1
cos
10
у
A
х
D
C
B
28.
№ 467 (а)Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
2 способ:
D1
1. Т.к. СD1|| ВА1, то углы
между ВD и ВА1; ВD и СD1 –
A1
равны.
2. В ΔВDА1: ВА1 = √5, А1D = √5
z
C1
B1
3. ΔВDА: по теореме Пифагора
BD AD 2 AB 2
BD 2
4. По теореме косинусов:
A1 D 2 A1 B 2 BD2 2 A1 B BD cos
1
cos
у
A
10
х
D
C
B























 Математика
Математика