Похожие презентации:
Средние значения в статистике
1.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИГосударственное автономное профессиональное образовательное
учреждение Московской области
«Подмосковный колледж «Энергия»
Индивидуальный проект по дисциплине:
«Математика» на тему:
Средние значения в статистике
Выполнили:
Студенты группы 1ОЛЛ121Э
Муйдинов Е.C
Левчук Д.В.
Преподаватель Поморцева
В.В
Оценка защиты:«»
Дата защиты:"„
2.
Вставьте заголовок слайда3. ПОНЯТИЕ СРЕДНЕЙ ВЕЛИЧЕНЫ
ПОНЯТИЕ СРЕДНЕЙВЕЛИЧЕНЫ
x
СРЕДНЯЯ ВЕЛИЧИНА В
СТАТИСТИКЕ-ОБОБЩАЮЩИЙ
ПОКАЗАТЕЛЬ,ХАРАКТЕРИЗУЮЩИ
Й ТИПИЧНЫЙ УРОВЕНЬ
ЯВЛЕНИЯ,СВОДНАЯ
ХАРАКТЕРИСТИКА
ЗАКОНОМЕРНОСТЕЙ ТОГО
ПРОЦЕССА,В КОТОРЫХ ОН
ПРОТЕКАЕТ.
4.
-Величины, в которых находят выражениеобщие условия, закономерность изучаемого
явления;
Средние
величины...
-Величины, отражающие то общее, что
складывается в каждом единичном
объекте;
-Обобщенная количественная признака в
статистической совокупности в
конкретных условиях места и времени;
-Является обобщением какого-то одного
свойства изучаемого явления или процесса.
5.
Определяющее свойство среднейИсходное соотношение ИСС:
ИСС=
Суммарное значение осредняемого
показателя
Количество единиц совокупности (объём)
6.
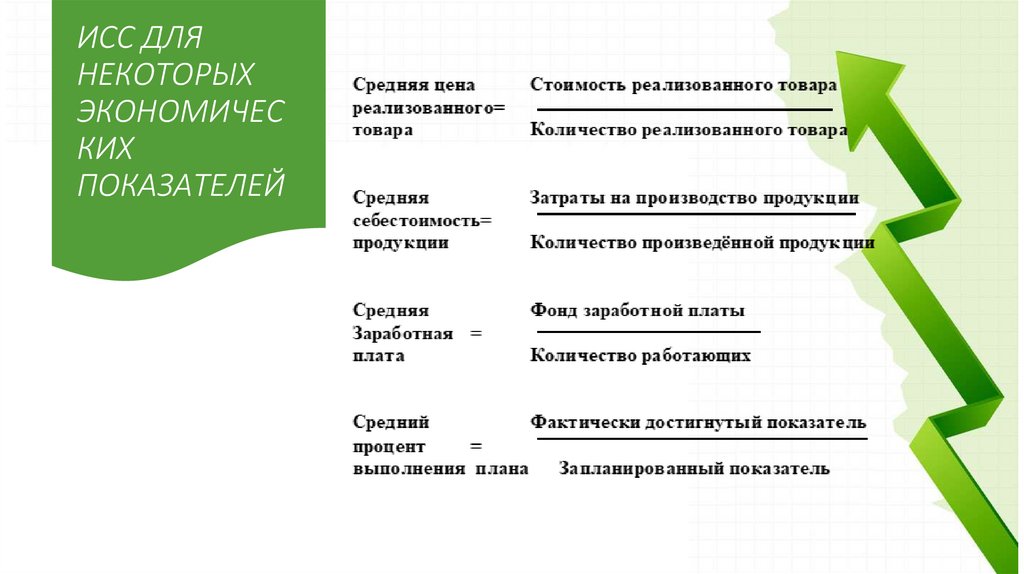
ИСС ДЛЯНЕКОТОРЫХ
ЭКОНОМИЧЕС
КИХ
ПОКАЗАТЕЛЕЙ
7. ВИДЫ СРЕДНИХ ВЕЛИЧИН В СТАТИСТИКЕ
ВИДЫ СРЕДНИХ ВЕЛИЧИН ВСТАТИСТИКЕ
vСредняя арифметическая
(простая, взвешенная, средняя из
групповых средних);
vСредняя гармоническая;
vСредняя геометрическая;
vСредняя степенная (квадратическая,
кубическая и т.д.);
vСтруктурные средние.
8. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА
СРЕДНЯЯАРИФМЕ
ТИЧЕСКА
Я ВЕЛИЧ
ИНА
Используется для расчёта
среднего значения признака
при известном объёме
совокупности
9. Средняя арифметическая простая
Используется длярасчёта среднего
значения признака при
известных
индивидуальных значениях
признака
(для несгруппированных
данных)
10. Средняя арифметическая взвешенная
Средняяарифметическая взвешенная
Вычисляется, если имеются
многократные
повторения значения признака и
совокупность разбита на
группы, используется для
расчёта среднего
значения группировочного призна
ка
(при сгруппированных данных)
11.
СРЕДНЯЯ ГАРМОНИЧЕСК
АЯ
Используется
при неизвестном объёме
совокупности или
необходимости обобщения
величины, обратной
изучаемому признаку.
12.
СРЕДНЯЯГЕОМЕТРИЧ
ЕСКАЯ
Используется для расчёта
средних
темпов и коэффициентов
роста
в рядах динамики
13.
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
x
n
1
x
n
1
i
несгруппированные
данные
14.
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
n
x
M
i
1
n
1
1 x M i
i
сгруппированные
данные
M i xi f i
15.
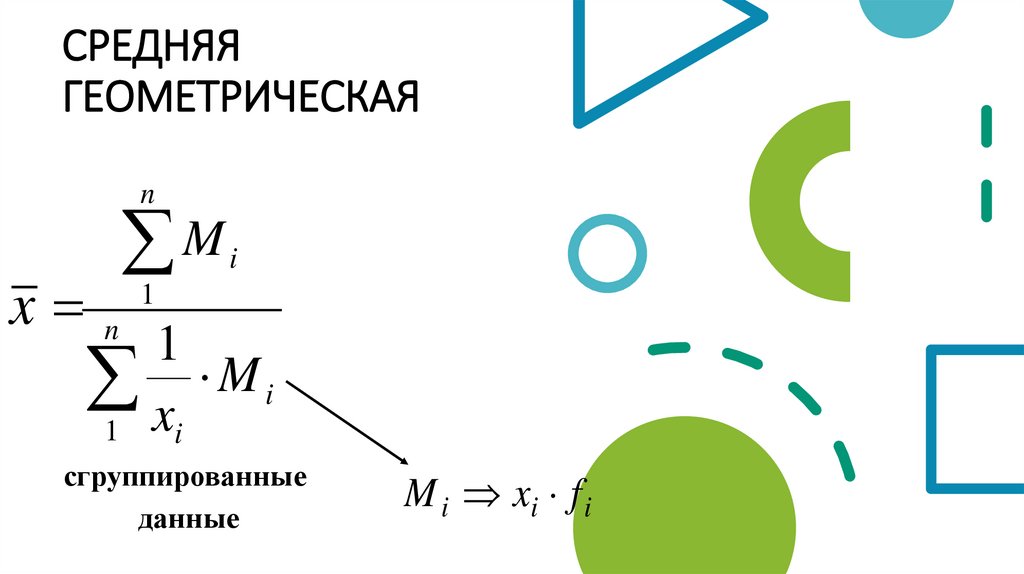
СРЕДНЯЯГЕОМЕТРИЧЕСКАЯ
n
x
M
i
1
n
1
1 x M i
i
сгруппированные
данные
M i xi f i
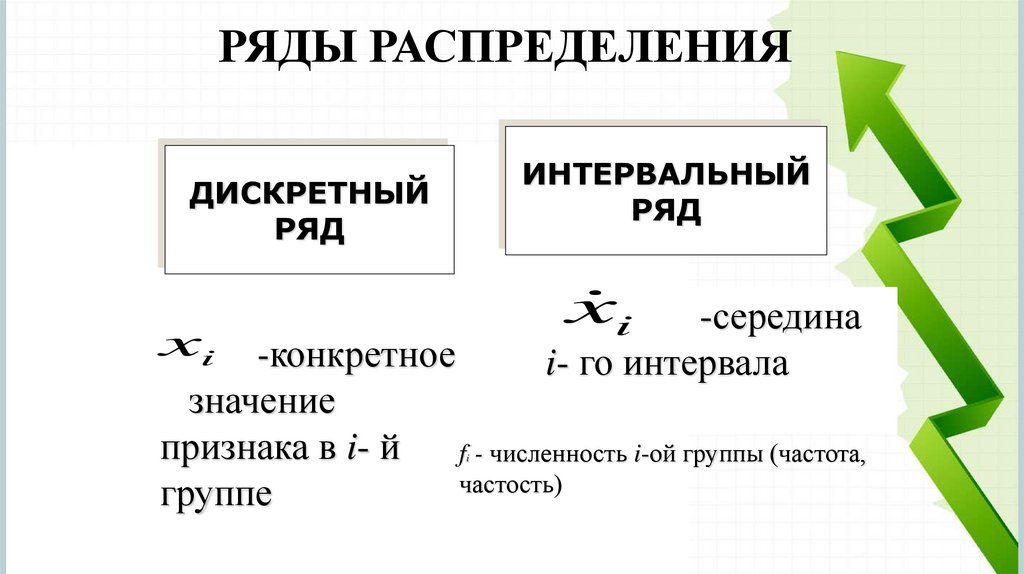
16. РЯДЫ РАСПРЕДЕЛЕНИЯ
ИНТЕРВАЛЬНЫЙРЯД
ДИСКРЕТНЫЙ
РЯД
i
x
-середина
i- го интервала
xi -конкретное
значение
признака в i- й
f - численность i-ой группы (частота,
частость)
группе
i
17.
СТРУКТУРНЫЕ СРЕДНИЕВЕЛИЧИНЫ
18.
МоМода (Мо) - значение
признака наиболее
часто встречающееся
в вариационном ряду.
19.
МеМедиана (Ме) - значение
варьирующего признака,
приходящееся на середину
ряда, варианта, делящая
ряд на две равные части
20.
СТАТИСТИЧЕСКИЕРЯДЫ
Вариационные
ряды
несгруппированные
данные
Атрибутивные
ряды
сгруппированные
Ряды
данные
распределения
первичные
дискретные
ранжированные
интервальные
21. РАНЖИРОВАННЫЙ РЯД
Медиана - центральная вариантапри нечетном числе единиц
совокупности, при четном числе
она равна полусумме серединных
вариант
(Моды не существует!)
22. ПЕРВИЧНЫЙ РЯД
Моды и медианыпервичного ряда не
существует!
23.
СТРУКТУРНЫЕ СРЕДНИЕ ДЛЯСГРУППИРОВАННЫХ ДАННЫХ
Определение:
Кумулятивная частота (Si)
результат суммирования
предшествующей кумулятивной частоты с
частотой текущей группы. Для первой группы
кумулятивная частота равна частоте в группе.
Si Si 1 f i ,
где i изменяется от 1
24.
ДИСКРЕТНЫЕ РЯДАРАСПРЕДЕЛЕНИЯ
МОДА
дискретного
ряда
МЕДИАНА
дискретного
ряда
определяется
по наибольшей
частоте
признака
определяется
по кумулятивной
частоте
признака
25. ДИСКРЕТНЫЙ РЯД
Мода и медиана - конкретныеварианты
•Мода - варианта с максимальной
частотой,
•Медиана - варианта с с кумулятивной
частотой, превышающей полусумму
частот
f
S
2
Ме
i
26. ИНТЕРВАЛЬНЫЙ РЯД РАСПРЕДЕЛЕНИЯ
• МОДА и МЕДИАНА• определяются по специальной методике
27. ИНТЕРВАЛЬНЫЙ РЯД
•Определение 1•Модальный интервал - интервал с
максимальной частотой
•Определение 2
•Медианный интервал - интервал, у
которого кумулятивная частота не
менее полусуммы частот
f
S
2
Ме
i
28. МОДА
M o xМof M o f M o 1
( f M o f M o 1 ) ( f M o f M o 1 )
hМo
29. МЕДДИАНА
f iS M e 1
2
M e xМe
hМe
fMe
Астафурова И.С.
30. Выводы:
Выбор формулы длярасчёта среднего
значения признака
начинается с построения
ИСС;
Основные виды средних
величин в статистике средняя
арифметическая,
средняя гармоническая и
средняя геометрическая;
Окончательный выбор
формулы зависит от вида
исходных данных.
31. Выводы:
Мода и медианаописывают структуру
совокупности по
изучаемому
признаку;
Для первичного ряда
моды и медианы не
существует;
Для ранжированного
ряда существует
только медиана;
Для дискретного
ряда мода и медиана
- конкретные
значения признака,
для интервального
мода и медиана
рассчитываются по
формулам.
Выводы:


























 Математика
Математика








