Похожие презентации:
Средние величины
1. Средние величины
2. План лекции:
5.1. Сущность и значение средней величины5.2. Виды средних величин
5.3. Средняя арифметическая
5.4. Средняя гармоническая
5.5. Средняя геометрическая
5.6. Средняя квадратическая
5.7. Степенные средние
5.8. Структурные средние (мода и медиана)
3. Средняя величина
представляет собой обобщеннуюколичественную характеристику
признака в статистической
совокупности в конкретных условиях
места и времени.
4. Категорию средней можно раскрыть через понятие ее определяющего свойства.
Эту величину можно представить в видефункции:
f ( X1, X2, ....., Xn )
Если в приведенной выше функции все
величины Х1, Х2.......Хп заменить их
средней величиной Х, то значение этой
функции должно остаться прежним:
f ( X1, X2, ...... Хn ) =f ( X, X, ......, X)
5. исходное соотношение средней (ИСС)
На практике определить среднюю во многихслучаях можно через исходное
соотношение средней (ИСС) или ее
логическую формулу:
ИСС= Суммарное значение или объем усредняемого признака
Число единиц или объем совокупности.
6. формы средней величины:
средняя арифметическая,средняя гармоническая,
средняя геометрическая,
средняя квадратическая, кубическая и.т.д.
Перечисленные средние объединяются в
общей формуле средней степенной (при
различной величине k):
__
X
K
K
x
fi
f
i
7. Средняя арифметическая простая (невзвешенная).
Эта форма средней используется втех случаях, когда расчет
осуществляется по
несгруппированым данным.
8.
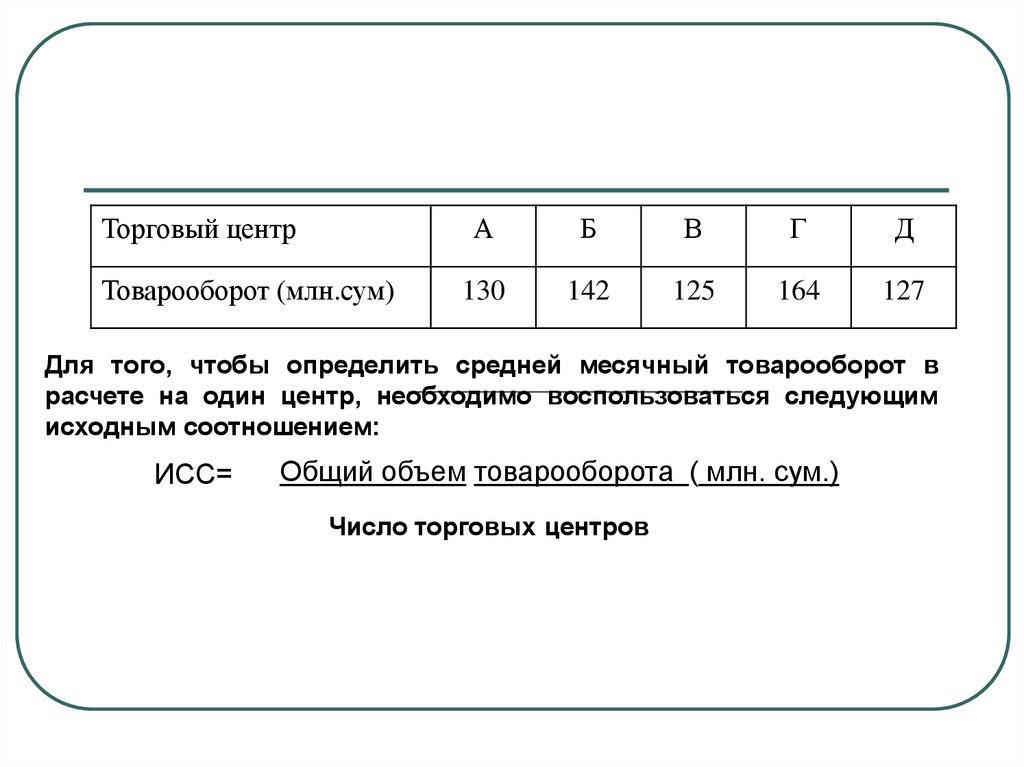
Торговый центрТоварооборот (млн.сум)
А
Б
В
Г
Д
130
142
125
164
127
Для того, чтобы определить средней месячный товарооборот в
расчете на один центр, необходимо воспользоваться следующим
исходным соотношением:
ИСС=
Общий объем товарооборота ( млн. сум.)
Число торговых центров
9. Запишем формулу данной средней
X 1 X 2 ... Xn X iX
n
n
С учетом имеющихся данных получим:
130 142 125 164 127
X
137,6 млн. сум
5
__
10. Рассмотрим следующий пример:Продажа акций АО “Дока-хлеб” на торгах фондовой биржы ( данные условные)
Сделка1
2
3
Количество
проданных
акции, шт
500
300
1100
Курс продажи
1080
1050
1145
11.
ИСС= Общая сумма сделок ( сум )Количество проданных акций ( шт)
___
X
xf
f
i i
i
1080 500 1050 300 1145 1100 2114500
X
1112.9
500 300 1100
1900
___
12. Расчет средней в интервальном ряду
Возраст (лет)Число менеджеров (чел).
до 25
25-30
30-40
40-50
50-60
60-и более
7
13
38
42
16
5
Итого
121
13.
___X
xf
f
i i
i
___
X
22.5 7 27.5 13 35 38 45 42 55 16 65 5
41
7 13 38 42 16 5
14. Свойства средней арифметической
1. Произведение средней на суммучастот равно сумме произведений
отдельных вариантов на
соответствующим им частоты:
___
X fi X i fi
15.
2. Сумма отклоненийиндивидуальных значений
признака от средней
арифметической равна нулю:
( X
___
i
X ) f i 0
16.
Сумма квадратов отклоненийиндивидуальных значений признака от
средней арифметической меньше, чем
сумма квадратов их отклонений от любой
другой произвольной величины С:
2
___
___
___
2
2
(
X
C
)
f
(
X
X
C
)
f
(
X
X
)
(
X
C
)
i
i
i
i
fi
___
___
___
___
___
( X i X ) 2 2( X i X )( X C ) ( X C ) 2 f i ( X i X ) 2 f i
___
___
___
2
(
X
C
)
(
X
X
)
f
(
X
C
)
fi
i
+2
i
17.
Следовательно сумма квадратов отклоненийиндивидуальных значений признака от
произвольной величины С больше суммы
квадратов их отклонений от своей средней на
величину
___
___
( X C)
2
fi или( X C )
2
f
i
18.
Если все усредняемые варианты уменьшитьили увеличить на постоянное число, А, то
средняя арифметическая соответственно
уменьшится или увеличится на ту же
величину:
( X A) f
f
i
i
i
X f Af
f f
i i
i
i
i
___
X A
19.
Если все варианты значений признакауменьшит или увеличить в А раз, то средняя
также соответственно увеличится или
уменьшится А раз:
Xi
1
A fi A X i fi 1 ___
X
A
fi
fi
20.
все веса уменьшить илиувеличить в А раз, то средняя
арифметическая от этого не
изменится:
Если
fi
1
X i A A X i fi ___
X
fi
1
fi
A
A
21. Средняя гармоническая взвешенная.
Данная форма используется, когдаизвестен числитель исходного
соотношения средней, но неизвестен
его, знаменатель.
___
X
X
i
i
i
22. Средняя гармоническая невзвешенная
Эта форма средней, используемаязначительно реже, имеет следующий
вид:
___
X
n
1
Xi
23. Средняя геометрическая.
Еще одной формулой, по которойможет осуществляться расчет
среднего показателя, является
средняя геометрическая:
___
X
X 1 X 2 X 3 .... X K
K
X X 1m1 X 2m 2 X
m
___
m3
3
K
X
... X Kmi m X imi
i
24. Средняя квадратическая.
В основе вычислений ряда сводныхстатистических показателей лежит
средняя квадратическая.
__
X
___
X
2
X
i
n
2
X
i fi
f
i
25. Структурные средние
Мода представляет собой значениеизучаемого признака, повторяющееся
и наибольшей частотой.
Медианой называется значение
признака, приходящееся на середину
ранжированной (упорядоченной)
совокупности.
26. Главное свойство медианы
заключается в том, что суммаабсолютных отклонений значений
признака от медианы меньше, чем от
любой другой величины:
X
i
Me min
27. Определение моды и медианы по интервальным рядам
МодаMo Xo I
( f Mo f Mo 1 )
( f Mo f Mo 1 ) ( f Mo f Mo 1 )
где Хо — нижняя граница модального интервала (модальным
наывается интервал, имеющий наибольшую частоту)
iвеличина модального интервала:
fMo частота модального интервала,
fMo1 частота интервала, предществующего модальному:
fMo+1частота интервала, следующего за модальным.
28.
Медиана.1
f i S Me 1
Ме X o I 2
f Me
где Хо нижняя граница медианного интервала (медианным
называется первый интервал, накопленная частота которого превышает
половину общей суммы частот);
Iвеличина медианного интервала:
Sme-1 - накопленная частота интервала, предшествующего медианному;
fme - частота медианного интервала.



























 Математика
Математика








