Похожие презентации:
Элементы теории относительности
1. ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
2. Пространство и время в Ньютоновской механике
• Пространство 3 мерно• Время независимо от пространства
• Размеры тел и промежутки времени
одинаковы во всех системах отсчета
• Если на тело не действуют силы, то оно
находится в состоянии покоя или
движется равномерно и прямолинейно
3.
• Уравнения механики не меняются припереходе из одной системы отсчета в
другую
• Взаимодействие тел распространяется
мгновенно
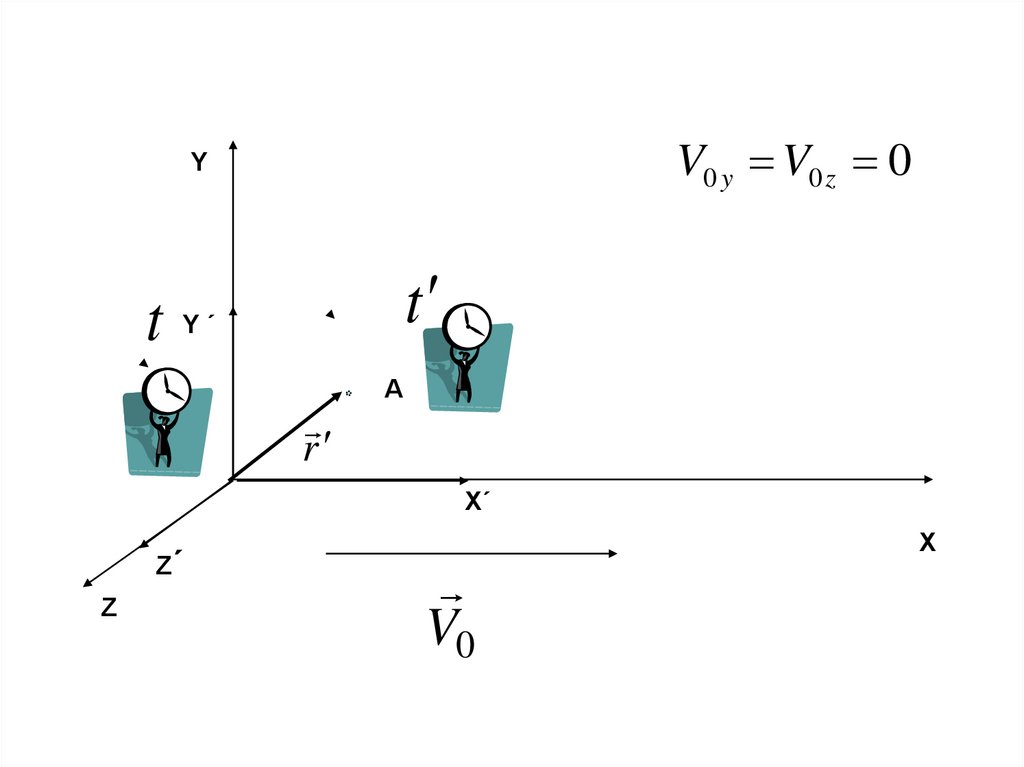
4. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
5.
V0 y V0 z 0Y
t
t
Y´
r
A
X´
Z´
Z
V0
X
6.
x x V0ty y
z z
t t
ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
7.
V V0 VdV dV0 dV
dt
dt
dt
dV
a
dt
dV
a
dt
a a
V0 const
t t
dV0
0
dt
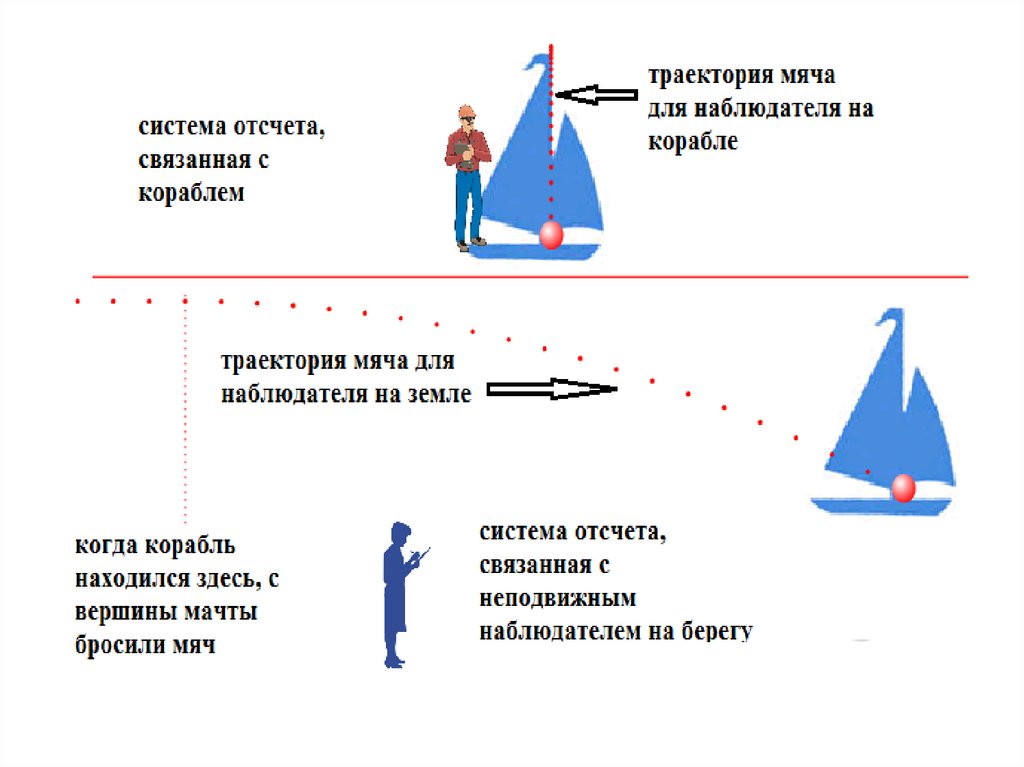
8. Принцип относительности Галилея
• Все законы механики имеютодинаковую форму во всех
инерциальных системах отсчета
9.
10. ПОСТУЛАТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (ПОСТУЛАТЫ ЭЙНШТЕЙНА)
• Все законы физики не меняются припереходе от одной инерциальной
системы отсчета к другой
• Скорость света в вакууме одинакова во
всех системах отсчета
C 3 10
8
м/с
11. Синхронизация часов
• Для описания события необходимоуказать место и время
• Чтобы корректно описывать время в
различных точках одной системы
отсчета часы должны быть
синхронизированы
12.
• Одновременность событий зависит отсистемы отсчета
• В ньютоновской механике это
достигалось за счет мгновенного
распространения сигнала
13. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
• Линейная связь между координатой ивременем
• При малых скоростях должны
переходить в преобразования Галилея
• Должны учитывать, что существует
максимальная скорость - с
14.
YK
V
Y΄
Х
Z
K΄
Х΄
Z΄
В начальный момент начала отсчета двух систем
совпадают и вдоль оси х посылают световой сигнал
X ct
X ct
Расстояние, которое пройдет
световой сигнал в системе К
Расстояние, которое пройдет
световой сигнал в системе К`
15.
X ( X Vt )X ( X Vt )
ct (ct Vt )
ct (ct Vt )
ctct tt (c V ) (c V )
c (c V )
2
2
2
2
2
16.
2c
2
2
c V
2
1
2
V
1 2
c
17.
K K XX Vt
Y Y
2
V
1 2
c
VX
t 2
c
t
2
V
1 2
c
Z Z
18.
K K X X Vt2
V
1 2
c
VX
t 2
c
t
2
V
1 2
c
Y Y
Z Z
19.
• Преобразования К ́–К и К- К ́ симметричны,отличаются знаком
• Время течет по-разному в различных
системах отсчета
• Нельзя говорить отдельно о пространстве и
отдельно о времени, существует единое
пространство -время
• При малых скоростях (V<<c) преобразования
Лоренца переходят в преобразования
Галилея
• При V >c исчезает физический смысл
20. СЛЕДСТВИЯ ИЗ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
21. Понятие одновременности
• Пусть в системе К происходят двасобытия А (x1,y1,z1,t1)
B (x2,y2,z2,t2)
• Найдем промежуток времени между
этими событиями в системе К ́
22.
VX 1t1 2
c
t1
2
V
1 2
c
VX 2
t2 2
c
t 2
2
V
1 2
c
V ( X 2 X1)
(t 2 t1 )
2
c
t2 t1
2
V
1 2
c
23.
• Если события одновременны в однойсистеме отсчета
t2 t1
t2 t1
V ( X 2 X1)
0
c2
2
V
1 2
c
Совсем не обязательно одновременны в другой
24.
X 2 X1(
t
t
)
2
1
t2 t1
2
V
1 2
c
t2 t1
t2 t1
ЕСЛИ СОБЫТИЯ ОДНОМЕСТНЫ И ОДНОВРЕМЕННЫ
В ОДНОЙ СИСТЕМЕ ОТСЧЕТА ,
ТО ОНИ ОДНОВРЕМЕННЫ В ЛЮБОЙ ДРУГОЙ
25. ДЛИТЕЛЬНОСТЬ СОБЫТИЙ В РАЗЛИЧНЫХ СИСТЕМАХ ОТСЧЕТА
• Пусть в некоторой покоящейся точкесистемы К происходит событие
длительностью Δt
• Найдем длительность этого события в
движущейся системе К ΄
26.
t t2 t1VX 1
t1 2
c
t1
2
V
1 2
c
t
VX 2
t2 2
c
t 2
2
V
1 2
c
t 2 t1
2
V
1 2
c
27.
• Длительность события –минимальна втой системе отсчета, относительно
которой тело покоится
t0 t2 t1
t
t 0
- Собственное
время
Лоренцево замедление времени
2
V
1 2
c
28. ПРИМЕР РАСПАД ПИОНА
• Π-мезон – положительно заряженнаячастица
m 273me
• Время жизни пиона в системе отсчета ,
где он покоится
2,5 10 c
8
V 0,99995 c
29.
• С точки зрения пиона он пройдет дораспада расстояние
V t0 0,99995 3 10 2,5 10 7,5 м
8
8
t
t 0
2
V
1 2
c
2,5 10
8
0,99995 c
1
2
c
6
2,5 10 c
2
2
30.
l V t6
0,99995 3 10 2,5 10 700м
8
31. ДЛИНА ТЕЛ В РАЗЛИЧНЫХ СИСТЕМАХ ОТСЧЕТА
• Пусть стержень покоится в системе К΄ ирасположен вдоль оси Х΄
• Найдем длину этого стержня в системе
отсчета К
• Чтобы измерить длину надо
одновременно засечь координаты
стержня в системе отсчета К
32.
X 2X 2 Vt
2
V
1 2
c
X 1
X 1 Vt
2
V
1 2
c
33.
X 2 X 1X 2 X1
l0 X 2 X 1
l X 2 X1
2
V
1 2
c
l0
l
2
V
1 2
c
34.
• В системе отсчета, относительнокоторой стержень покоится его длина
называется собственной l и
0
максимальна
• В движущихся относительно стержня
системах отсчета его длина
уменьшается
• Лоренцево сокращение длины
35. Релятивистский закон сложения скоростей
36.
• Пусть в К системе отсчета частицадвижется со скоростью
u (u x , u y , u z )
• Найдем проекции скорости в системе К ́
u (u x , u y , u z )
37.
dXu x
dt
dX
dX Vdt
2
V
1 2
c
VdX
dt 2
c
dt
2
V
1 2
c
38.
VdXdt 2
dX dX Vdt
c
2
2
dt
V
V
1 2
1 2
c
c
2
V
1 2
dX Vdt
c
2
VdX
V
dt
2
1 2
c
c
dX Vdt
VdX
dt 2
c
39.
dXV
dX
dt
dX
dt
V
dt
1
2
c
u X
uX V
V uX
1 2
c
40.
dYuY
dt
Y Y
dY dY
VdX
dt 2
c
dt
2
V
1 2
c
41.
VdXdt 2
c
uY dY
2
V
1 2
c
2
V
dY 1 2
c
VdX
dt 2
c
42.
2uY
dY
V
1 2
dt
c
dX
V
dt
1 2
c
2
V
uY 1 2
uY
c
V uX
1 2
c
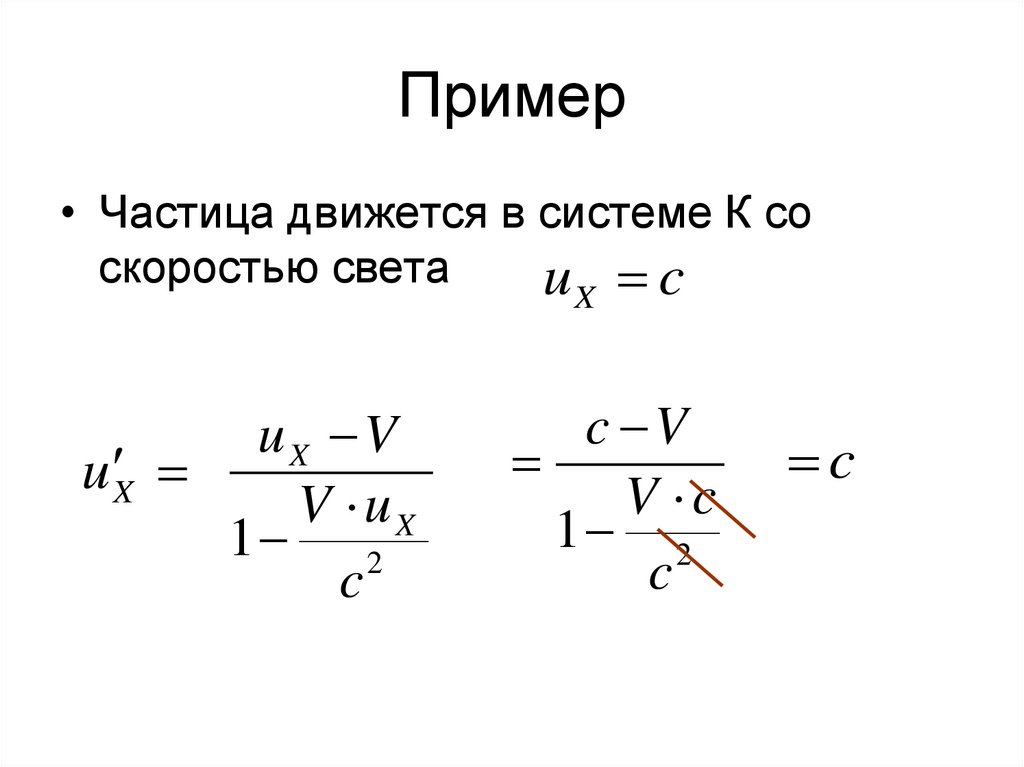
43. Пример
• Частица движется в системе К соскоростью света
u c
X
uX V
u X
V uX
1 2
c
c V
V c
1 2
c
c





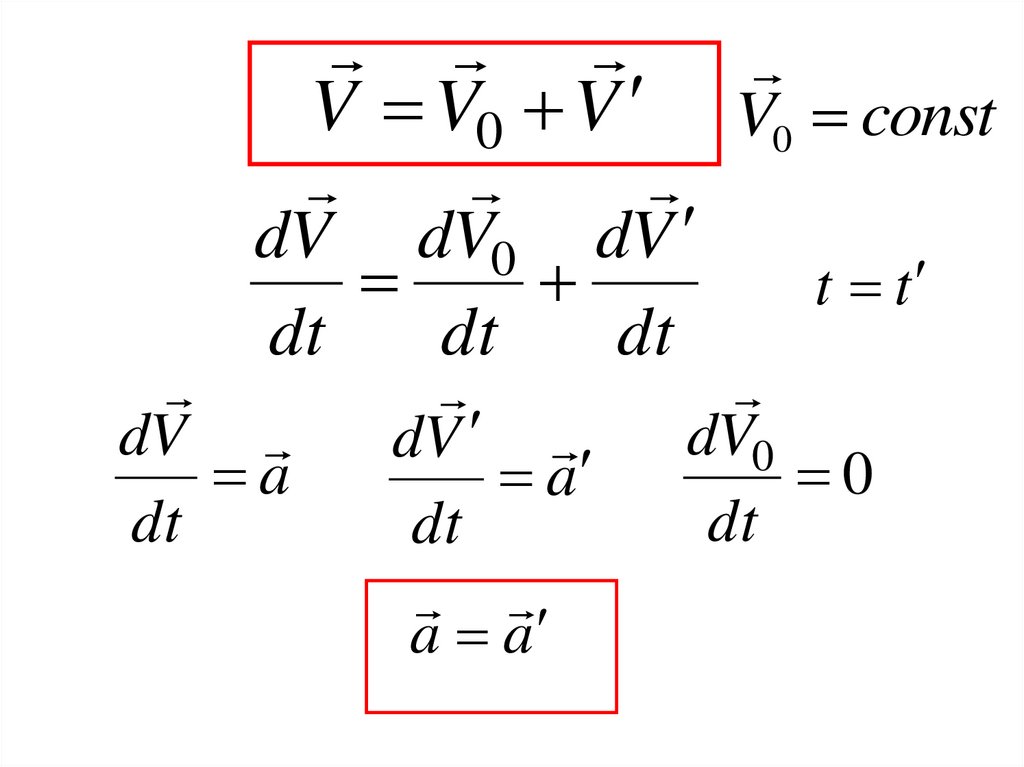








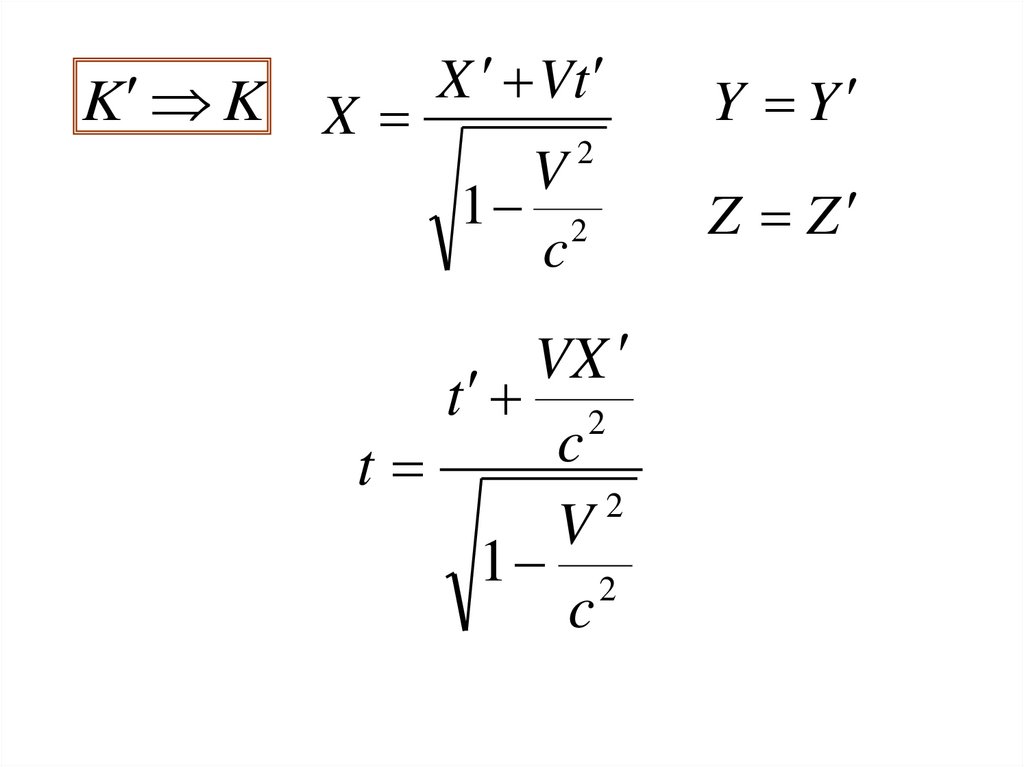




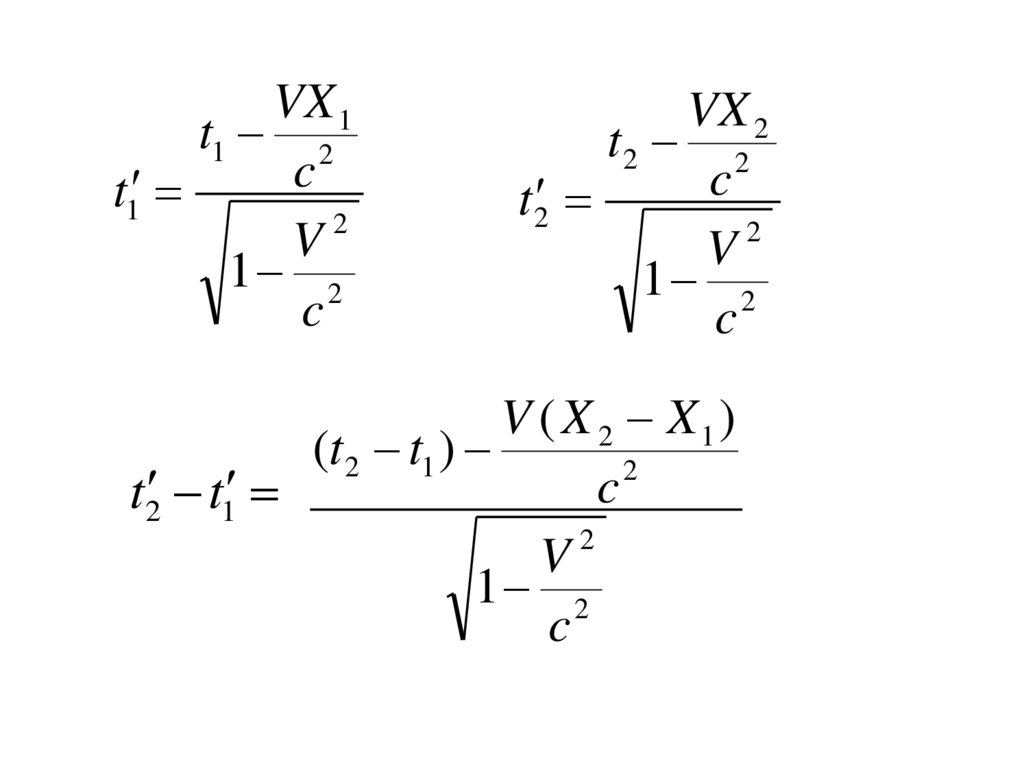







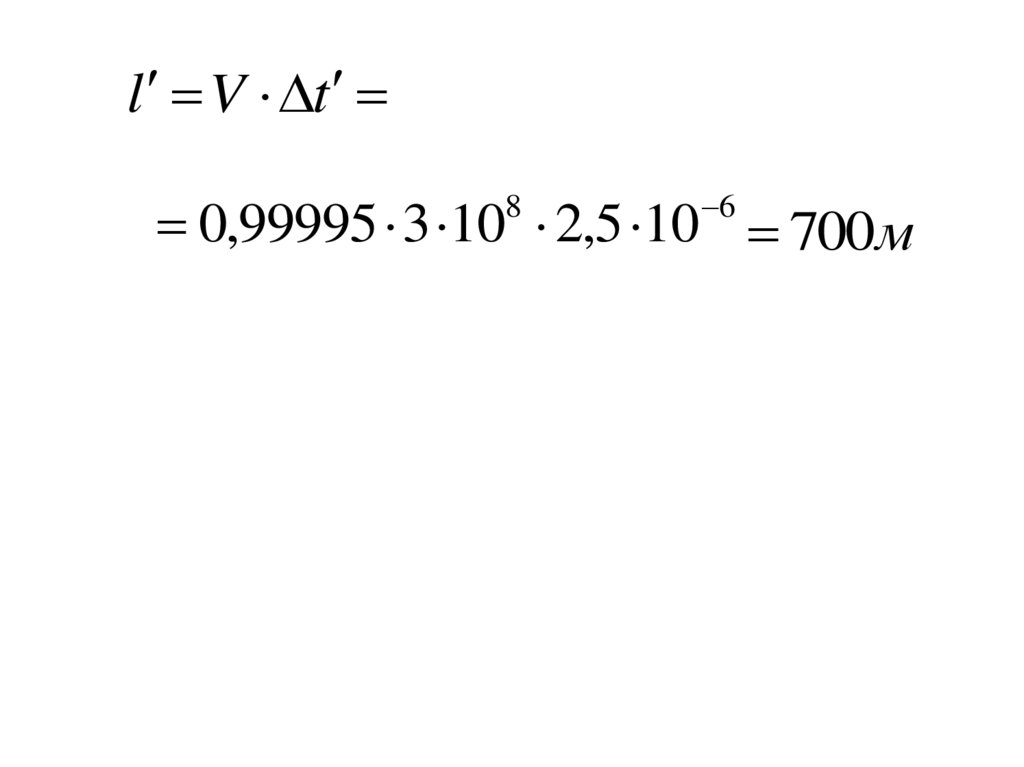


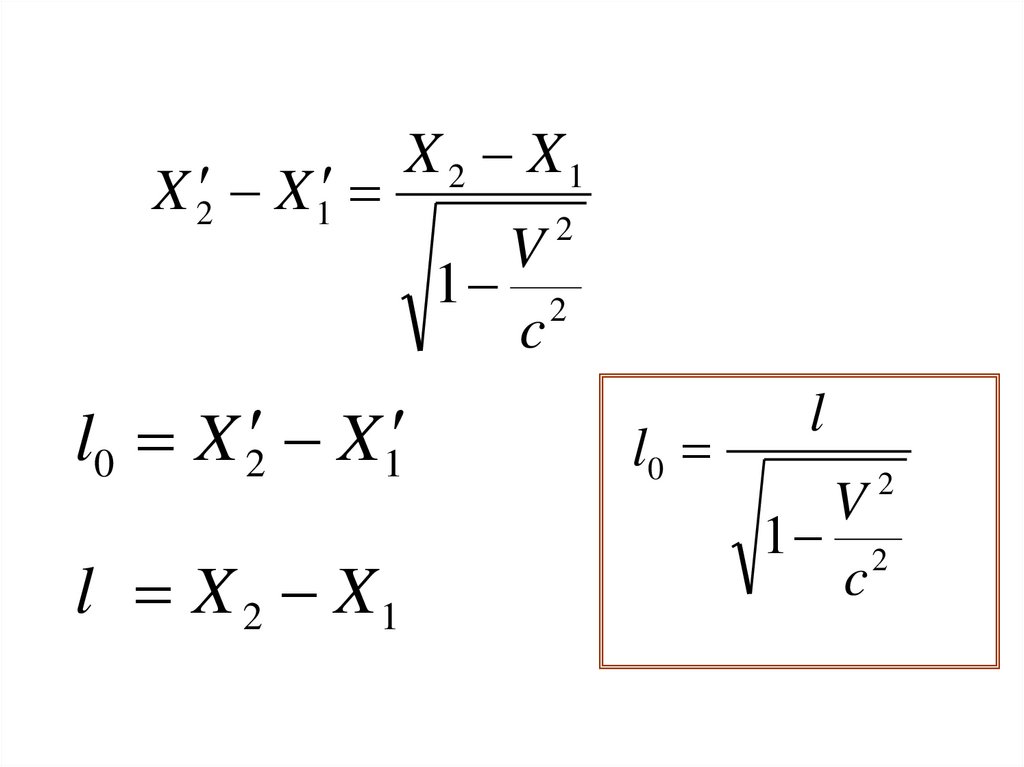



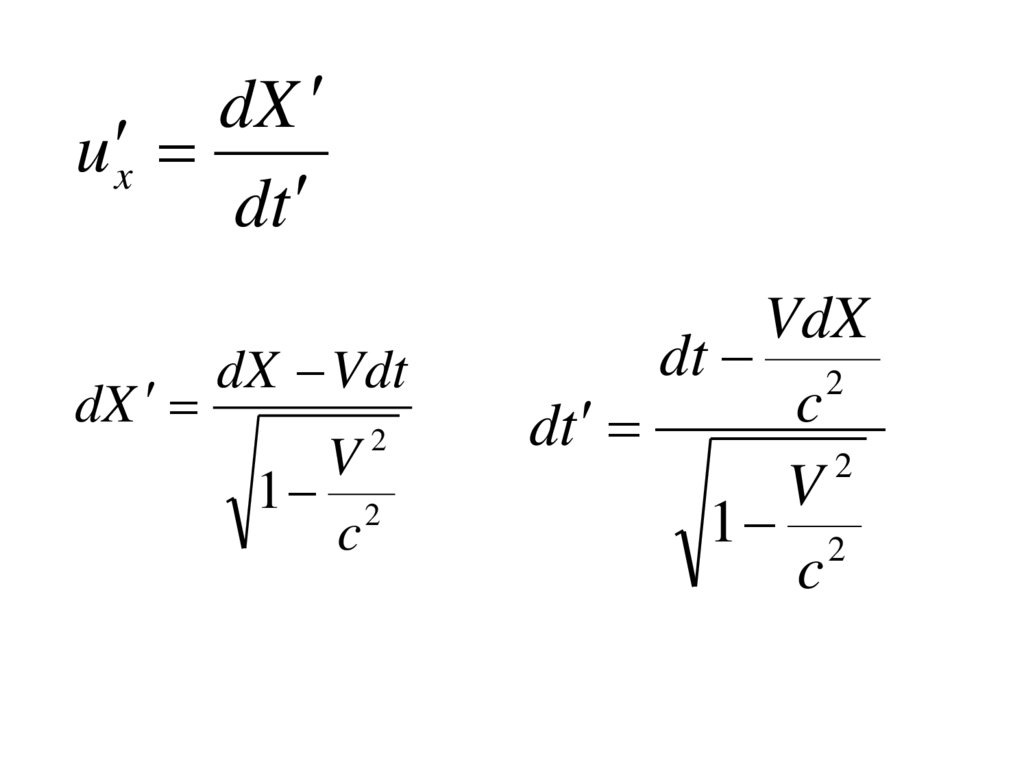
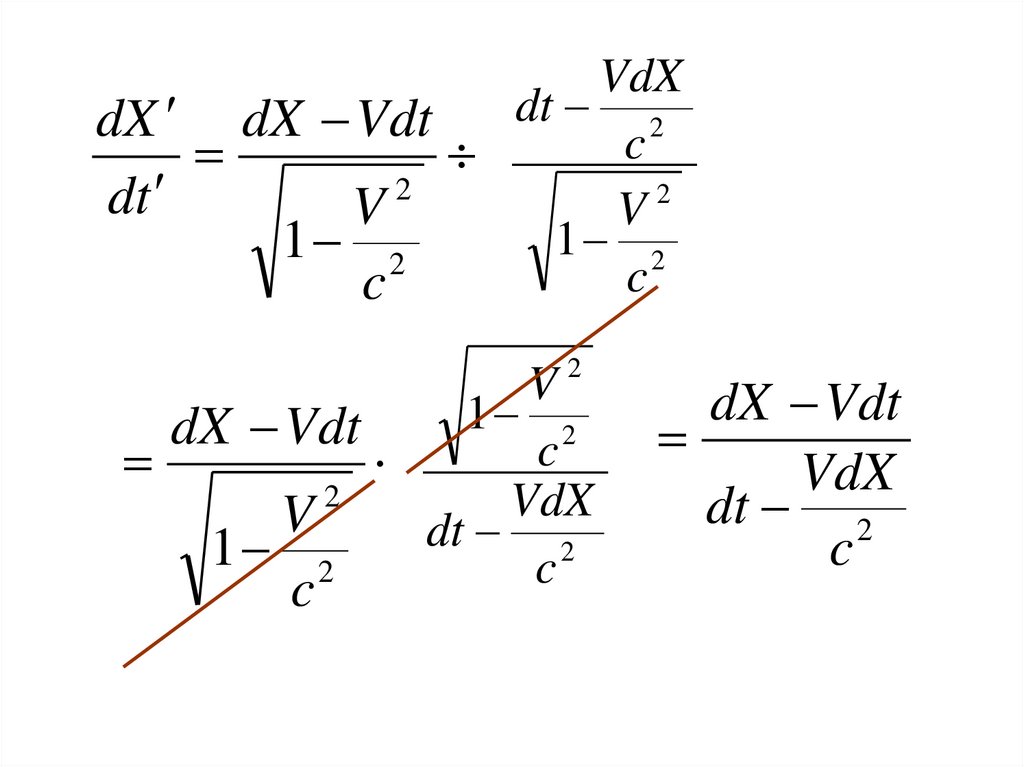
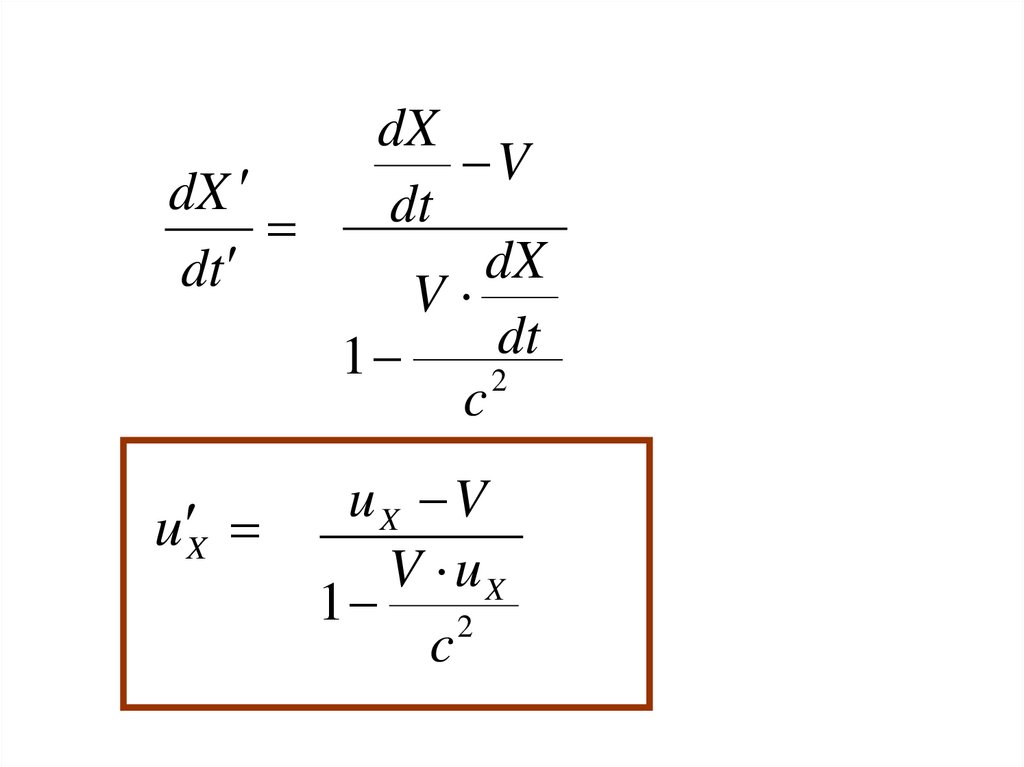
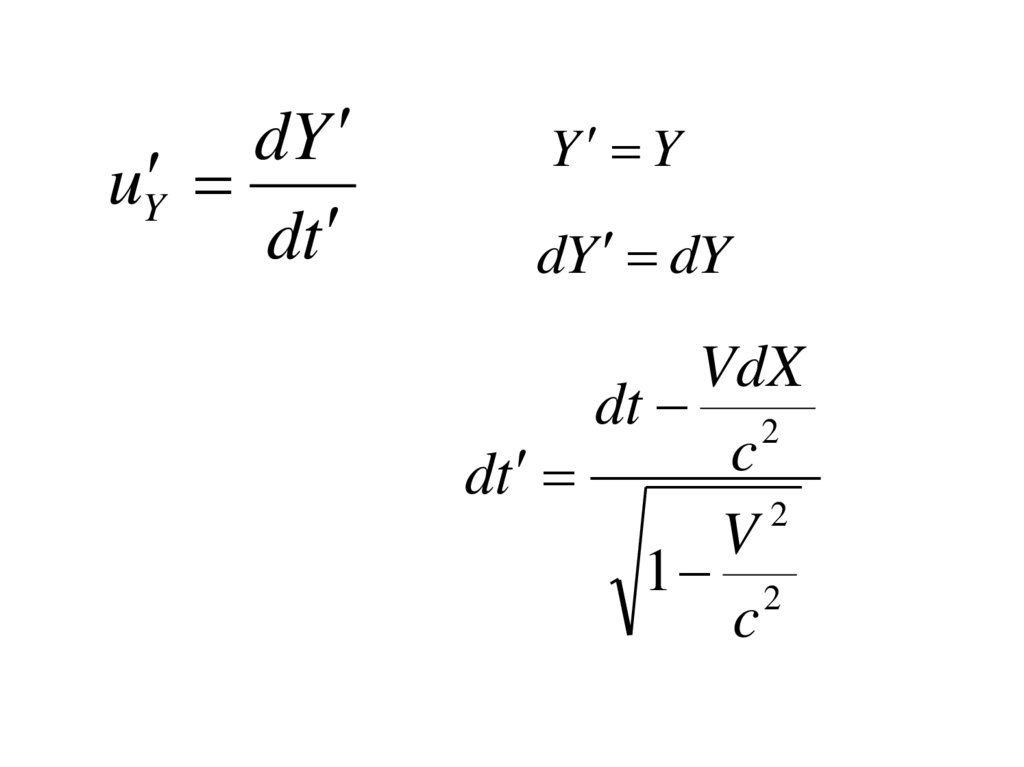
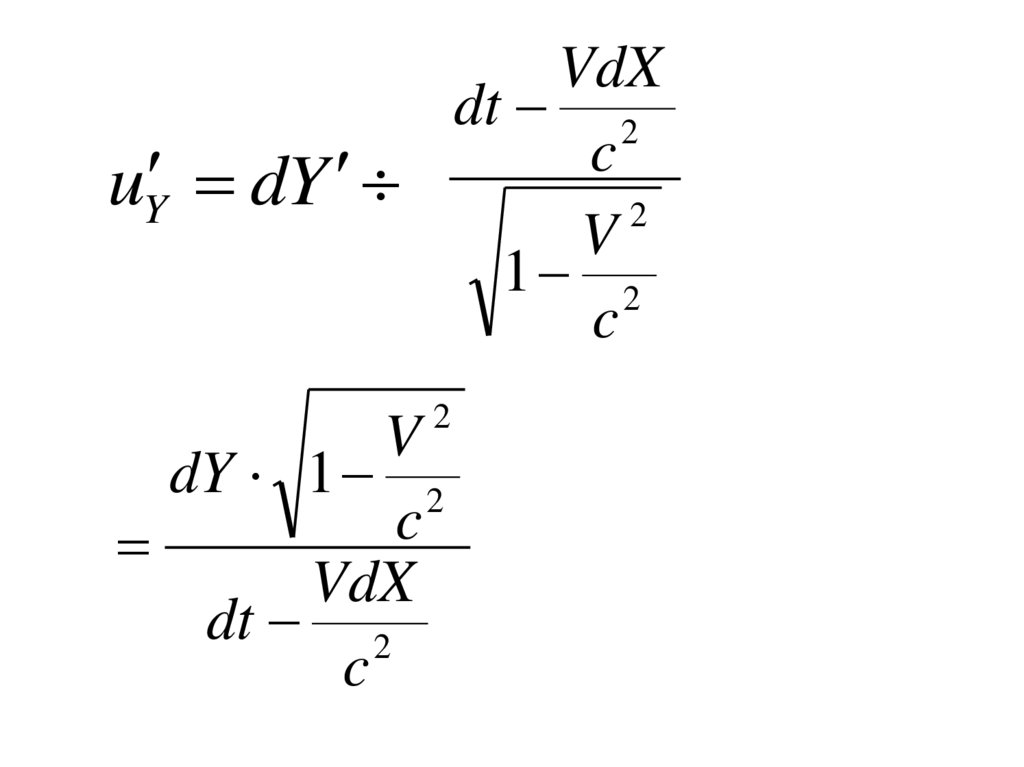

 Физика
Физика








