Равновесие при наличии трения

1.

Тема 7.
РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
7.1. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ.
Силой трения скольжения
называется сила сопротивления относительному
скольжению, которая возникает в плоскости
соприкосновения тел при движении одно тела по
поверхности другого .
Причины возникновения трения:
- шероховатость поверхностей, создающая
сопротивление перемещению;
- наличием сцепления у прижатых друг к другу тел.
1

2.

7.1. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ.
Формулировка законов трения скольжения
при покое.
1. При стремлении сдвинуть одно тело по
поверхности другого в плоскости соприкосновения
тел возникает сила трения (или сила сцепления),
которая может принимать любые значения от нуля
до значения Fпр называемого предельной силой
трения.
Приложенная к телу сила трения направлена в
сторону, противоположную той, куда
действующие на тело силы стремятся его
сдвинуть.
2

3.

7.1. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ.
Формулировка законов трения скольжения
при покое.
2. Предельная сила трения численно равна
произведению статического коэффициента трения
на нормальное давление или нормальную реакцию:
Fпр f0 N
Статический коэффициент трения f0 — величина
безразмерная; он определяется опытным путём и
зависит от материала соприкасающихся тел и
состояния поверхностей (характер обработки,
температура, влажность и т. п.).
3

4.

7.1. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ.
Формулировка законов трения скольжения
при покое.
3. Значение предельной силы трения в довольно
широких пределах не зависит от размеров
соприкасающихся при трении поверхностей.
Значение силы трения при покое определяется
неравенством
Fпр f0 N
следовательно, это значение может быть любым, но
не большим, чем Fnp.
Равновесие, имеющее место, когда сила трения
равна Fnp, будем называть предельным
4
равновесием.

5.

7.1. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ.
При движении сила трения скольжения направлена
в сторону, противоположную движению, и равна
произведению динамического коэффициента
трения на нормальное давление:
F f N
Динамический коэффициент трения скольжения f –
безразмерная величина определяемая опытным путём.
Значение f зависит:
- от материала и состояния поверхностей;
- от скорости движущихся тел (с увеличением скорости
коэффициент f сначала несколько убывает, а затем
сохраняет почти постоянное значение).
5

6.

7.2. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ.
Реакция реальной (шероховатой) связи слагается из двух
составляющих: из нормальной реакции N и
перпендикулярной ей силы трения F. Следовательно, полная
реакция R будет отклонена от нормали к поверхности на
некоторый угол .
При изменении силы трения от нуля
до Fпр сила R изменяется от N до
0
Rпр, а её угол с нормалью растёт от
нуля до некоторого предельного
значения 0 .
Наибольший угол 0 , который полная реакция
шероховатой связи образует с нормалью к
поверхности, называется углом трения.
Так как Fпр f 0 N , то
tg 0 f 0
tg 0
Fпр
N
6

7.

7.2. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ.
Приложим силу Р к телу, лежащему на шероховатой
поверхности. Пусть Р образует угол с нормалью к
поверхности.
Тело сдвинется только тогда, когда
сдвигающее усилие P sin
P cos
P
P sin
будет больше
Fпр f0 P sin
(весом тела пренебрежём).
т.е. F f 0 N , где N P cos
P sin f 0 P cos , но f 0 tg 0
tg tg 0 , т.е. 0
Следовательно, если сила образует с нормалью к
поверхности угол , меньший чем угол трения 0 ,
то она не может сдвинуть тело вдоль этой
7
поверхности.

8.

7.3. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ.
Изучение равновесия тел с учётом трения скольжения можно
свести к рассмотрению предельного равновесия, которое
имеет место, когда сила трения равна Fпр.
Алгоритм решения:
- реакцию R шероховатой связи представить в виде
двух её составляющих N и Fnp ;
- составить уравнения равновесия и присоединить к
ним равенство F f N .
пр
0
- из полученной системы уравнений и определить
искомые величины.
На чертеже реакцию шероховатой связи удобнее изображать
одной силой R, которая в предельном положении равновесия
отклонена от нормали к поверхности на угол 0 .
8

9.

7.3. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ.
Если в задаче надо определить значение силы трения F,
когда равновесие не является предельным и F Fпр , то эту
силу F следует считать неизвестной величиной и находить из
соответствующих уравнений равновесия.
Задача 1.
Груз весом Р=10 Н лежит на
горизонтальной плоскости.
Определить, какую силу Q,
направленную под углом α=30° к этой
плоскости, надо приложить к грузу,
чтобы сдвинуть его с места, если
статический коэффициент трения
груза о плоскость f=0,6.
9

10.

7.3. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ.
Решение:
1. Рассмотрим предельное
равновесие груза.
В этом состоянии на груз действуют
следующие силы:
P, Q, N, Fпр.
2. Введём оси координат x и y
(как показано на рисунке к задаче) и составим уравнения
равновесия системы в проекциях на эти оси.
1.
Fkx Q cos Fпр 0; Fky N Q sin P 0
2. N P Q sin Fпр f 0 N f 0 ( P Q sin )
f0 P
3. Q cos f 0 ( P Q sin ) 0, Q
cos f 0 sin
Q 5, 2 Н
10

11.

7.3. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ.
Решение:
3. Если к грузу приложить меньшую
силу, например силу Q 4 Н
то тогда сдвигающее усилие будет
равно Q cos30o 2 3 3,46 Н
Максимально возможную в этом случае силу трения можно
найти из соотношения
o
Fпр f0 ( P Q cos30 ) 4,8 Н
Q Fпр груз останется в покое.
4. Определим величину силу трения, которая удерживает груз
в равновесии.
F Q cos30o 3,46 Н Fпр 4,8 Н
11

12.

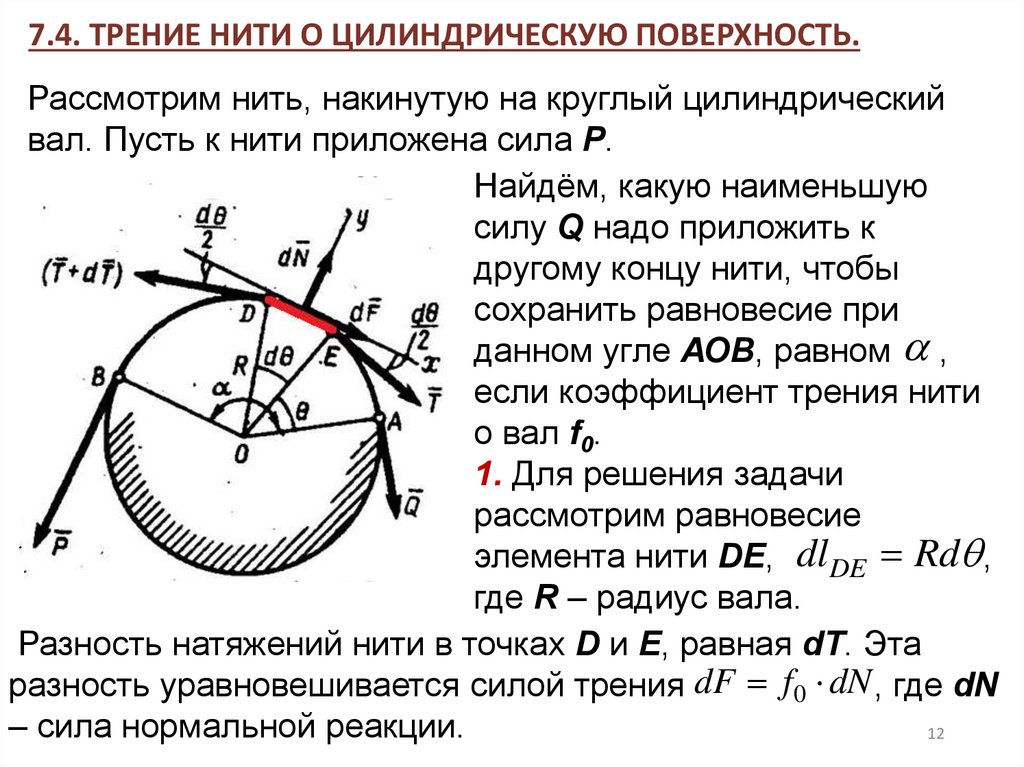
7.4. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ.
Рассмотрим нить, накинутую на круглый цилиндрический
вал. Пусть к нити приложена сила P.
Найдём, какую наименьшую
силу Q надо приложить к
другому концу нити, чтобы
сохранить равновесие при
данном угле АОВ, равном ,
если коэффициент трения нити
о вал f0.
1. Для решения задачи
рассмотрим равновесие
элемента нити DE, dlDE Rd ,
где R – радиус вала.
Разность натяжений нити в точках D и Е, равная dТ. Эта
разность уравновешивается силой трения dF f 0 dN , где dN
– сила нормальной реакции.
12

13.

7.4. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ.
2. Равновесие является
предельным при наименьшем
значении Q.
dТ f 0 dN
Значение dN определим из
уравнения равновесия в проекции
на ось у.
Fky 0 :
Полагая синус малого
угла равным самому
углу, найдём
2Td
dN
Td
2
d
d
dN T sin
(T dT )sin
0
2
2
d
d
dN T sin
(T dT )sin
2
2
13

14.

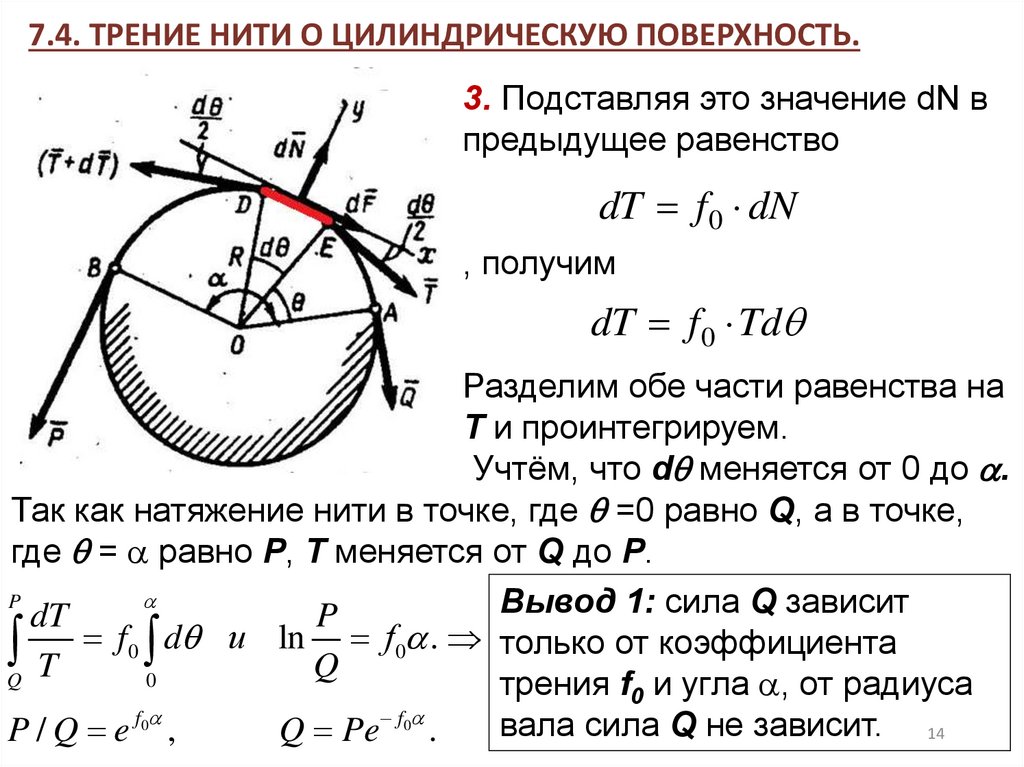
7.4. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ.
3. Подставляя это значение dN в
предыдущее равенство
dT f 0 dN
, получим
dT f 0 Td
Разделим обе части равенства на
Т и проинтегрируем.
Учтём, что d меняется от 0 до .
Так как натяжение нити в точке, где =0 равно Q, а в точке,
где = равно P, Т меняется от Q до Р.
P
Вывод 1: сила Q зависит
dT
P
Q T f0 0 d и ln Q f0 . только от коэффициента
трения f0 и угла , от радиуса
вала сила Q не зависит. 14
P / Q e f0 ,
Q Pe f0 .

15.

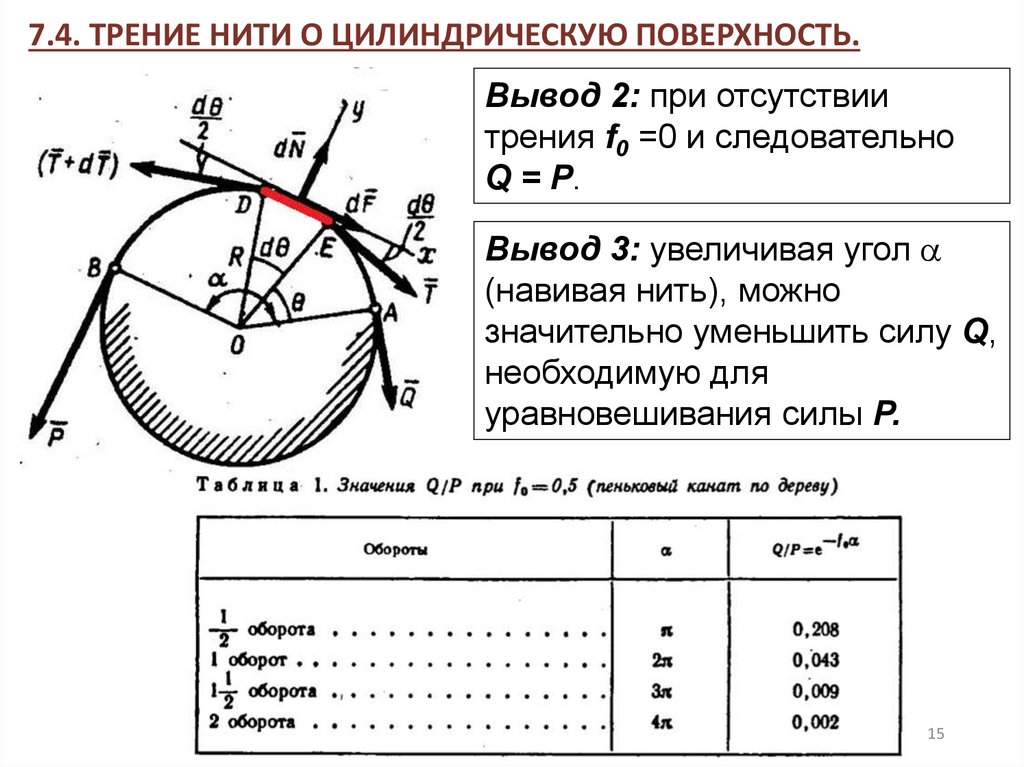
7.4. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ.
Вывод 2: при отсутствии
трения f0 =0 и следовательно
Q = Р.
Вывод 3: увеличивая угол
(навивая нить), можно
значительно уменьшить силу Q,
необходимую для
уравновешивания силы Р.
15