Похожие презентации:
Равновесие при наличии трения
1.
Новосибирский Государственный Архитектурно-СтроительныйУниверситет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
СТАТИКА
ЛЕКЦИЯ 8.
РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
Кафедра теоретической механики
2. План лекции
•ВведениеКаждым тяжелым телом побеждается
сопротивление трения, равное четвертой
части этого веса.
Леонардо да Винчи
•Равновесие при наличии трения скольжения
•Равновесие при наличии трения качения
•Какое движение (скольжение или качение)
реализуется на практике
•Заключение
3. На предыдущей лекции
Равновесиесистемы тел
ВВЕДЕНИЕ
4. Цель лекции
Разобратьсяс реакцией связи шероховатой
(не гладкой) поверхности
ВВЕДЕНИЕ
5. Что дает принцип освобождаемости от связей ?
То, что реакция связи должна быть направлена в сторону,противоположную той, куда связь не дает перемещаться.
Однако, с шероховатой поверхностью не все так просто!
F
Что подсказывает опыт?
Если
F Fmax
Тело начнет либо скользить, либо
катиться.
Каким именно будет движение – в общем случае не очевидно !
ВВЕДЕНИЕ
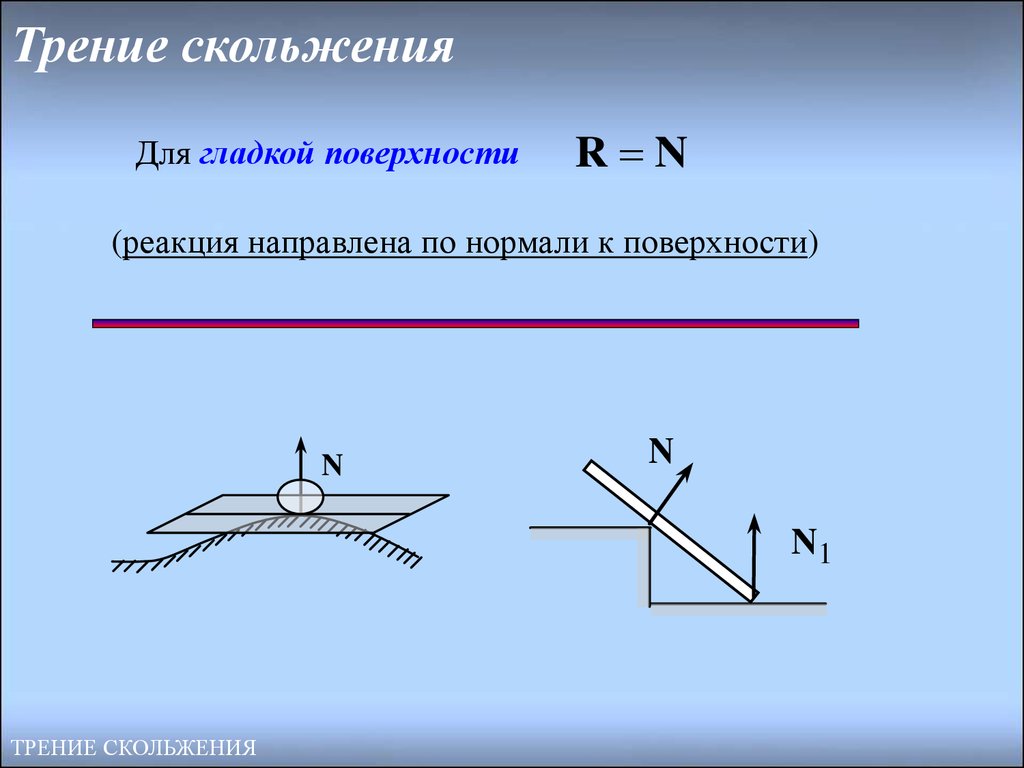
6. Трение скольжения
Для гладкой поверхностиR N
(реакция направлена по нормали к поверхности)
N
N
N1
ТРЕНИЕ СКОЛЬЖЕНИЯ
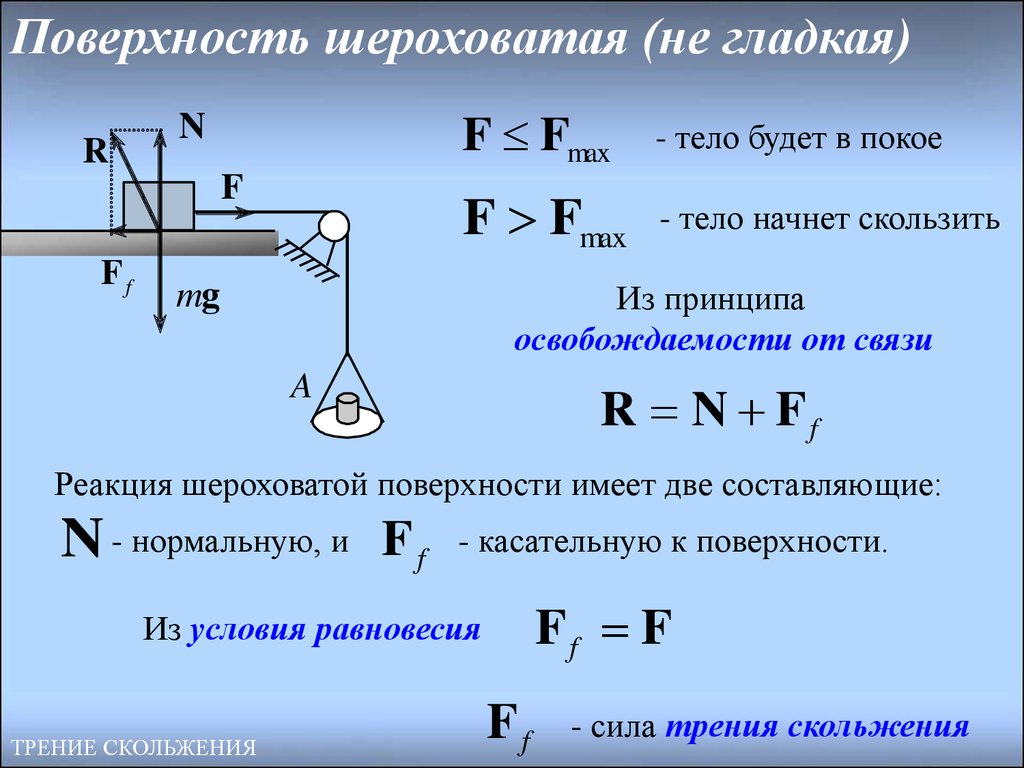
7. Поверхность шероховатая (не гладкая)
RN
F
Ff
F Fmax
- тело будет в покое
F Fmax
- тело начнет скользить
Из принципа
освобождаемости от связи
mg
A
R N Ff
Реакция шероховатой поверхности имеет две составляющие:
N - нормальную, и F f
- касательную к поверхности.
Ff F
Из условия равновесия
ТРЕНИЕ СКОЛЬЖЕНИЯ
Ff
- сила трения скольжения
8. Замечание 1
Природа возникновения сил трения скольжения сложнаи не до конца изучена. Она связана как с микрошеротоватостями, так и с диффузией.
Как описать
Связаны ли
Ff
Ff
и
N
Законы трения скольжения (Амонтона-Кулона)
1)
Ff
направлена в сторону, противоположную той,
куда активные силы стремятся сдвинуть тело.
2) Модуль силы
3)
fs
Ff
0 Ff F
пред
f
F
пред
f
fs N
- статический коэффициент трения скольжения,
зависит только от материалов соприкасающихся тел и
не зависит от площади их соприкосновения.
ТРЕНИЕ СКОЛЬЖЕНИЯ
9. Замечание 2
Законы трения носят приближенный характери применимы для покоящихся тел.
При движении
fd
Ff f d N
- динамический коэффициент трения скольжения
Как правило
fd fs
ТРЕНИЕ СКОЛЬЖЕНИЯ
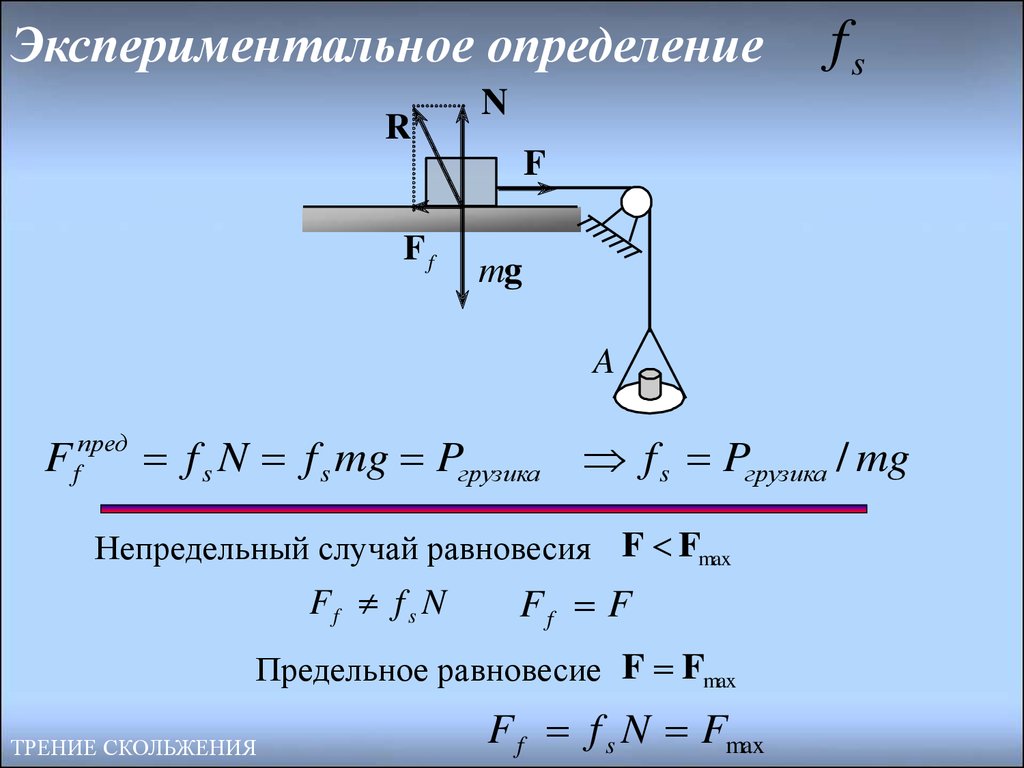
10. Экспериментальное определение
Rfs
N
F
Ff
mg
A
F fпред f s N f s mg Pгрузика f s Pгрузика / mg
Непредельный случай равновесия F Fmax
Ff f s N
Ff F
Предельное равновесие F Fmax
ТРЕНИЕ СКОЛЬЖЕНИЯ
F f f s N Fmax
11. Геометрическая интерпретация
R - отклонена от нормали к поверхностина угол
*
R
*
F *f
tg F f / N
0 пред
tg пред f s
пред
- называется углом трения
Конус с вершиной в точке касания и образующей, наклоненной
к нормали под углом трения, называется конусом трения.
При непредельном равновесии R
расположен внутри конуса трения
При предельном равновесии R
лежит на поверхности конуса трения
ТРЕНИЕ СКОЛЬЖЕНИЯ
12. Явление заклинивания
F Fy cosF sin
F - равнодействующая всех активных сил,
действующих на тело
- угол, который она составляет с нормалью
Вопрос: Сдвинется ли тело, если мы
будем увеличивать величину силу F не меняя
Ответ: Сдвинется, если
пред
И останется в покое, если пред
При любой, сколь угодно большой силе
F
Для доказательства достаточно
заметить, что
при равновесии R F и учесть, что сила R
не может находиться вне конуса трения.
Вывод: Если R лежит внутри конуса, то сколько ее
не увеличивай, тело не сдвинется (заклинится).
ТРЕНИЕ СКОЛЬЖЕНИЯ
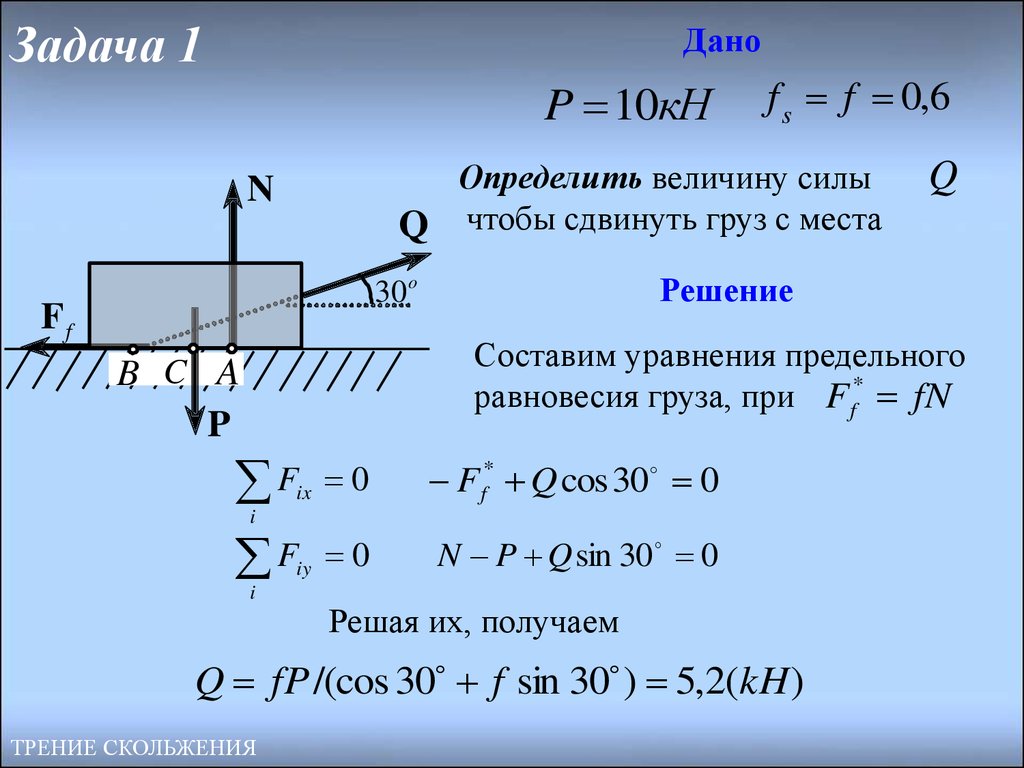
13. Задача 1
ДаноP 10кН
f s f 0,6
Определить величину силы
Q чтобы сдвинуть груз с места
N
Решение
30 o
Ff
Q
Составим уравнения предельного
равновесия груза, при F f* fN
B C A
P
Fix 0
F f* Q cos 30 0
i
Fiy 0
i
N P Q sin 30 0
Решая их, получаем
Q fP /(cos 30 f sin 30 ) 5,2(kH )
ТРЕНИЕ СКОЛЬЖЕНИЯ
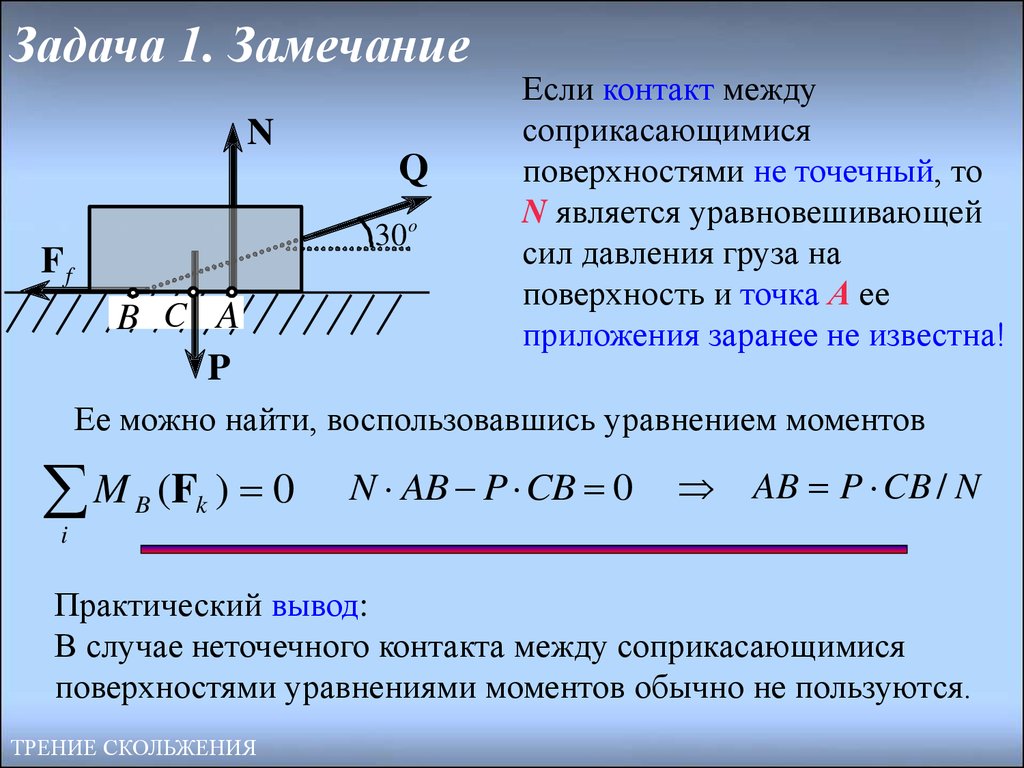
14. Задача 1. Замечание
NQ
30 o
Ff
B C A
P
Если контакт между
соприкасающимися
поверхностями не точечный, то
N является уравновешивающей
сил давления груза на
поверхность и точка А ее
приложения заранее не известна!
Ее можно найти, воспользовавшись уравнением моментов
M
B
(Fk ) 0
N AB P CB 0
AB P CB / N
i
Практический вывод:
В случае неточечного контакта между соприкасающимися
поверхностями уравнениями моментов обычно не пользуются.
ТРЕНИЕ СКОЛЬЖЕНИЯ
15. Задача 2
Дано:Q, , пред ,
Определить P при равновесии
Q
Решение:
P
a)
y
б)
Pmin
N
F
Очевидно, ответ будет иметь вид
*
f
x
y F *f
Q
N Pmax
x
Q
Pmin P Pmax
При P Pmin
Ff
- направлена вверх, по
наклонной плоскости
При P Pmax
Ff
ТРЕНИЕ СКОЛЬЖЕНИЯ
- направлена вниз, по наклонной плоскости
16. Задача 2. Продолжение 1
a)Pmin
N
y
F
P Pmin
x
*
f
уравнения равновесия имеют вид
F
ix
Q
0
Pmin fN Q sin 0
0
N Q cos 0
i
F
iy
i
так как
Pmin
f tg * ,
то
Q
*
*
Q sin tg Q cos
(sin
cos
sin
cos )
*
cos
*
Q sin( * ) / cos *
ТРЕНИЕ СКОЛЬЖЕНИЯ
17. Задача 2. Продолжение 2
б)y F *f
ТРЕНИЕ СКОЛЬЖЕНИЯ
N Pmax
x
Q
P Pmax
Pmax Q sin( * ) / cos *
18. Задача 2. Замечание
Для гладкой поверхностиPmax Pmin Qtg
Q
P Qtg
P
Малое отклонение (даже случайное) от этой величины
вызвало бы движение груза. Иными словами, для гладкой
поверхности положение равновесия неустойчиво.
Шероховатая же поверхность содержит конечный
интервал значений P [ Pmin , Pmax ]
Для которых тело находится в равновесии, причем этот
интервал тем шире, чем больше шероховатость.
Трение придает устойчивость равновесию,
а коэффициент трения f s
характеризует запас устойчивости.
ТРЕНИЕ СКОЛЬЖЕНИЯ
19. Трение качения
NN
Q
N
A
a)
Ff
N
P
N
Опыт подсказывает, что диск покатится лишь при
При Q Q max будет покой.
Из условий равновесия
Вместе с тем
M
Q Q max
F f Q, N P
A
(Fi ) 0 Q 0
i
Противоречие с опытом!
ТРЕНИЕ КАЧЕНИЯ
20. Трение качения 2
NN
Q
N
A
a)
Ff
N
P
N
б)
Ff
N
N Q
N N
k
A
B
P
N
Причина: Реальные тела – не абсолютно твердые.
Контакт – по площадке АВ (рис. б).
Qmax R Nk
ТРЕНИЕ КАЧЕНИЯ
k – коэффициент трения качения
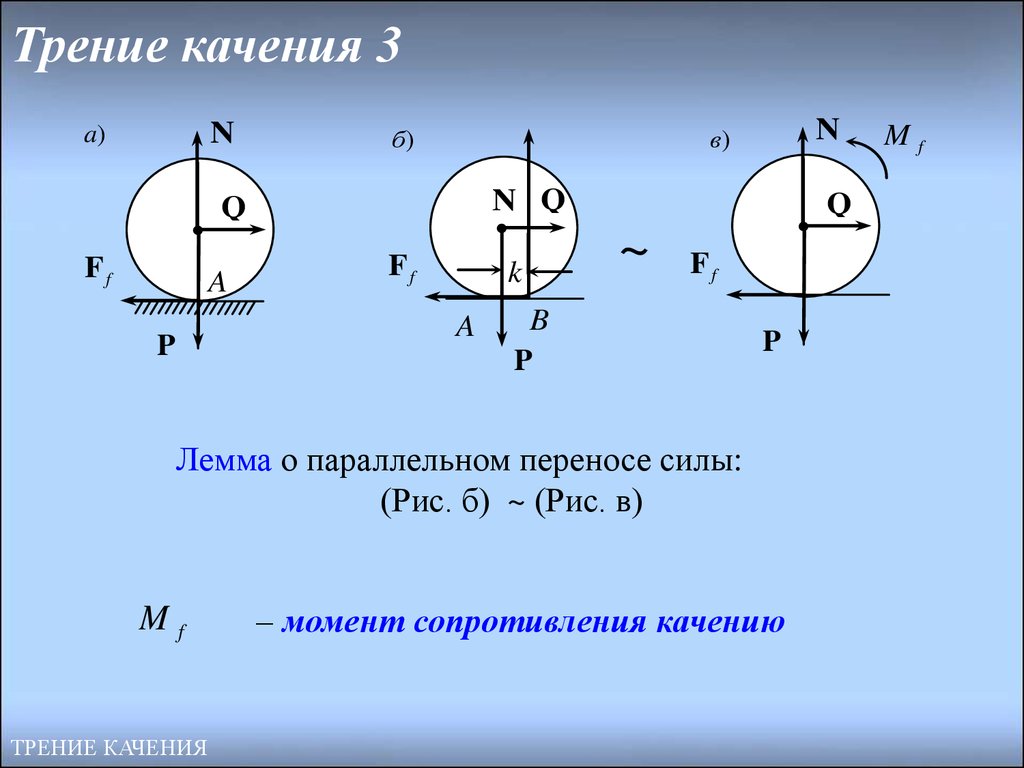
21. Трение качения 3
NN
Q
N
A
a)
Ff
б)
P
N
N Q
N N
k
Ff
N
N
N
N
Q
N
в)
A
B
P
N
~
Ff
N
P
N
Лемма о параллельном переносе силы:
(Рис. б) ~ (Рис. в)
Mf
ТРЕНИЕ КАЧЕНИЯ
– момент сопротивления качению
Mf
22. Аналог закона Амонтона-Кулона
NN
Q
N
в)
Ff
N
Mf
P
N
1. Направление M f - в сторону, противоположную той,
куда активные силы стремятся повернуть тело.
2. Величина
пред
M f : 0 M f M пред
,
M
kN
f
f
3. k – зависит лишь от свойств материалов
соприкасающихся тел.
ТРЕНИЕ КАЧЕНИЯ
23. Замечания
Замечание 1. В случае качения реакция шероховатойстенки состоит из силы R N Ff
и момента M . Т.е. в полном соответствии с принципом
освобождаемости от связи!
Замечание 2. Чем тверже тело, тем меньшее усилие
требуется, чтобы покатить тело. Например, вагон могут
катить 4 человека, а грузовой автомобиль нет, хотя он
значительно легче.
ТРЕНИЕ КАЧЕНИЯ
24. Задача 3
Дано:б)
a)
N
y
P 80H
Q
R 0.5м
1
2
Ff
Mf
А
P
Q 80 H
x
Определить:
наименьший k, при котором каток останется в покое
Замечание:
Предполагается, что каток не будет скользить
Ffmax f s N Q
ТРЕНИЕ КАЧЕНИЯ
25. Задача 3
Дано:б)
a)
N
y
Q
1
2
Ff
P 80H
Mf
А
P
R 0.5м
Q 80 H
x
Решение:
Система сил, действующих на каток, показана на (рис. б).
Уравнение моментов относительно точки А
M f kN
Q 2R M f 0
т.к. равновесие предельное k 2QR / N
Так как N=P, то k=0,008 м
Замечание: Рис.а задачи определяет простейший способ
нахождения k (при этом Q наименьший вес груза, при
котором каток начнет катиться).
ТРЕНИЕ КАЧЕНИЯ
26. Какое движение (скольжение или качение) реализуется на практике?
Nk
Ff
Q
Будем увеличивать силу Q
Вопрос: Диск покатится или заскользит ?
Пока диск в покое
P
Причем
F f Q, M f QR
F f f s N , M f kN
Т.е. в покое Q f s N , Q (k / R) N
Следовательно, режим движения будет определяться
соотношением f s и k/R
Ответ:
Если k / R f то диск покатиться,
если же k / R f то заскользит.
ТРЕНИЕ КАЧЕНИЯ ИЛИ СКОЛЬЖЕНИЯ
27. Пример. Колёса автомобиля
Для колес обычноk/R f
и они катятся без проскальзывания.
Но иногда
k/R f
и тогда колеса проскальзывают (зимой – по
льду, летом – по глинистой дороге после дождя).
ТРЕНИЕ КАЧЕНИЯ ИЛИ СКОЛЬЖЕНИЯ
28. Задача 4.
а)б)
F
F
О
A
Ff
Дано:
N
A
О
Mf
В
P
Определить:
Наибольшую F при равновесии ?
Решение
Из условий равновесия получаем
k 0,006 м
f 0,2
R 0,6 м
OA 0,4 м
ск
пред
F
0
F
F
fN fP 0,4кН
ix
max
f
i
пред
кач
кач
M
(
F
)
0
M
kN
kP
F
AB
F
P i
f
max
max 0,012кН
i
Максимальная сила, при которой каток еще будет в покое
Fmax F
кач
max
12кН
(при F 12кН каток начнет катиться)
ТРЕНИЕ КАЧЕНИЯ ИЛИ СКОЛЬЖЕНИЯ
29. Заключение
В случае скольжения:R N Ff
- реакция шероховатой поверхности
имеет две
N
Ff
составляющие: нормальную и касательную к
поверхности:
Ff f s N
- F f N в случае непредельного равновесия,
- f s в случае предельно равновесия.
В случае качения:
R N Ff
Mf
- реакция
состоит из силы
и момента
M f kN
- M kN в случае непредельного равновесия,
- f
в случае предельного равновесия.
В случае, когда тело может и скользить и катиться:
- если k / R f , тело заскользит,
- если
, тело покатится.
k/R f
ЗАКЛЮЧЕНИЕ
30. Вопросы для самоконтроля
1. Назовите особенности реакции шероховатойповерхности.
2. Что такое сила трения покоя?
3. Что такое сила трения скольжения?
4. Сформулируйте закон трения Амонтона-Кулона.
5. Как измерить коэффициент трения?
6. Что такое угол трения?
7. Что такое конус трения?
8. Какой коэффициент трения больше – покоя или
скольжения?
9. Как связан коэффициент трения с углом трения?
10. Что такое трение качения?
11. Сформулируйте закон трения качения?
12. В каком случае диск покатиться, а когда заскользит?
ЗАКЛЮЧЕНИЕ
31. Тема следующей лекции
Кинематика. Лекция 1.Способы задания движения точки.
Траектория и скорость точки.
ЗАКЛЮЧЕНИЕ

























 Физика
Физика Механика
Механика








