§8. Равновесие тела при наличии сил трения

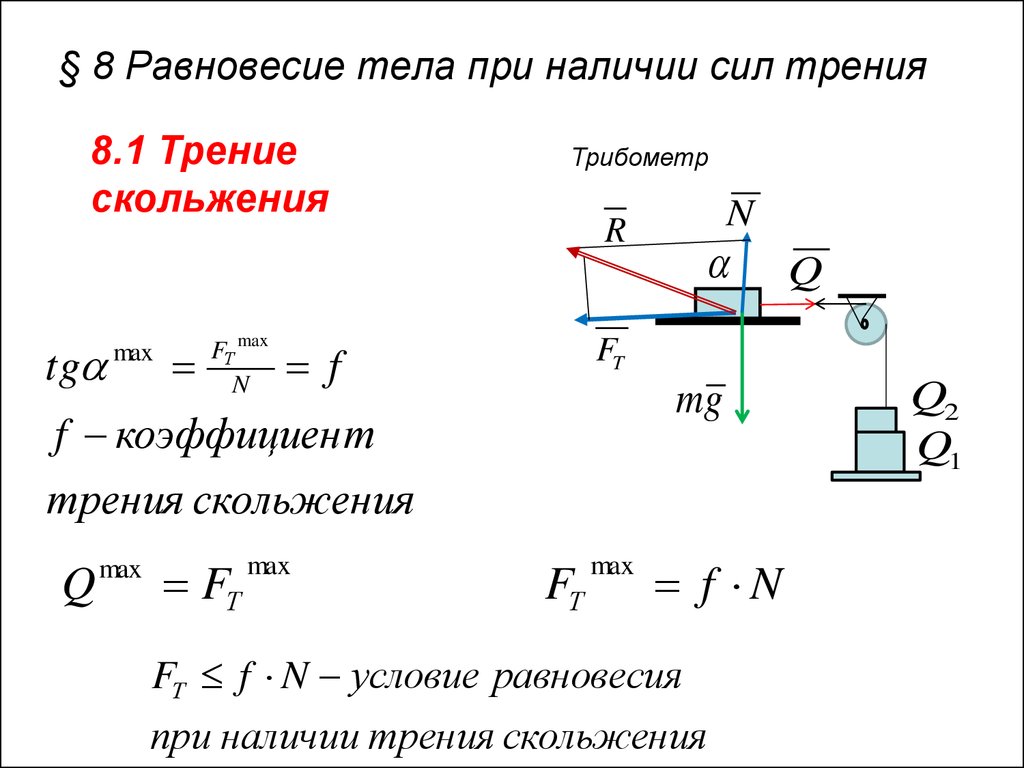
1. § 8 Равновесие тела при наличии сил трения

8.1 Трение
скольжения
tg
max
FТ max
N
Трибометр
f
Q
FТ
max
Q
FT
mg
f коэффициен т
трения скольжения
max
N
R
FТ
max
f N
FТ f N условие равновесия
при наличии трения скольжения
Q2
Q1

2.

8.2 Законы трения
1.FT
Противоположна направлению
вектора скорости;
2. FT
Не зависит от площади
соприкасающихся поверхностей;
3. FT
max
f N
4. Коэффициент трения скольжения
зависит от физических свойств
соприкасающихся поверхностей

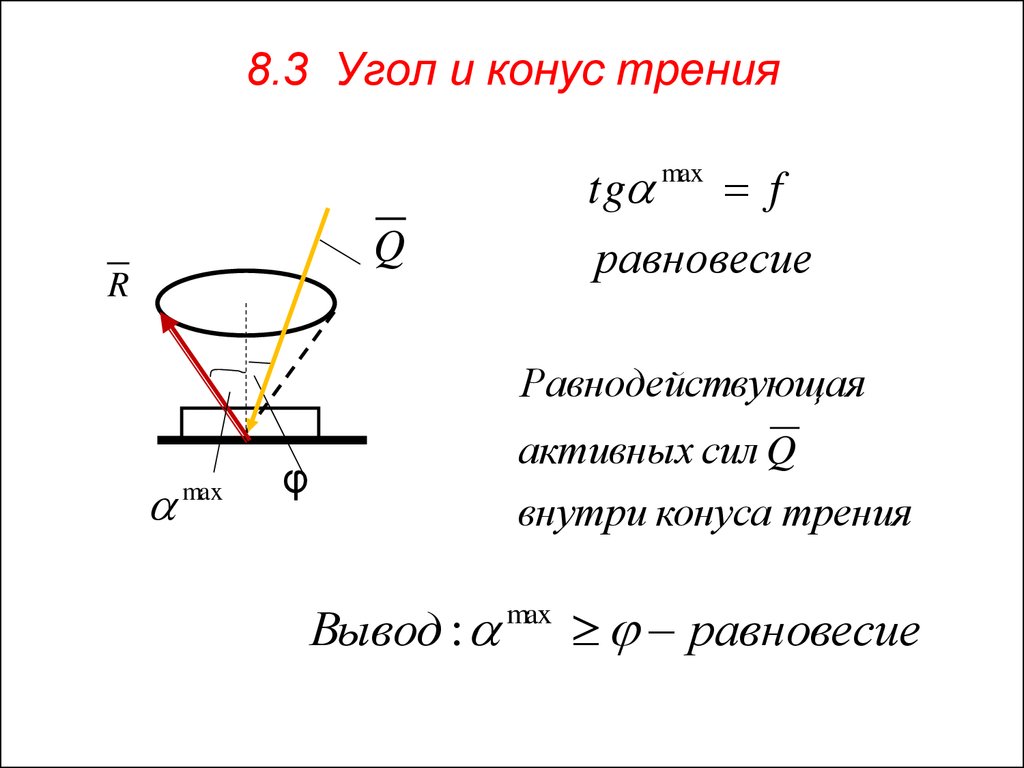
3. 8.3 Угол и конус трения

tg
Q
max
f
равновесие
R
Равнодействующая
max
активных сил Q
внутри конуса трения
φ
Вывод :
max
равновесие

4. Пример 1. Брус АВ весом P опирается на гладкую стену и шероховатый пол. f=0,15. Определить угол α при равновесии бруса.

Уравнения равновесия
y
F
ky
NA
A
NB P
NB
P
α
О
FТ
B
x
a
m
N
a
P
A B
2 FТ a tg 0
N B P2 FТ tg
Условие равновесия при
f P
tg
FT
P
2 tg
наличии трения скольжения
FT f N
Обозначим OB a
P
2 tg
N B P 0
1
2f
tg 3,3; ответ : 730

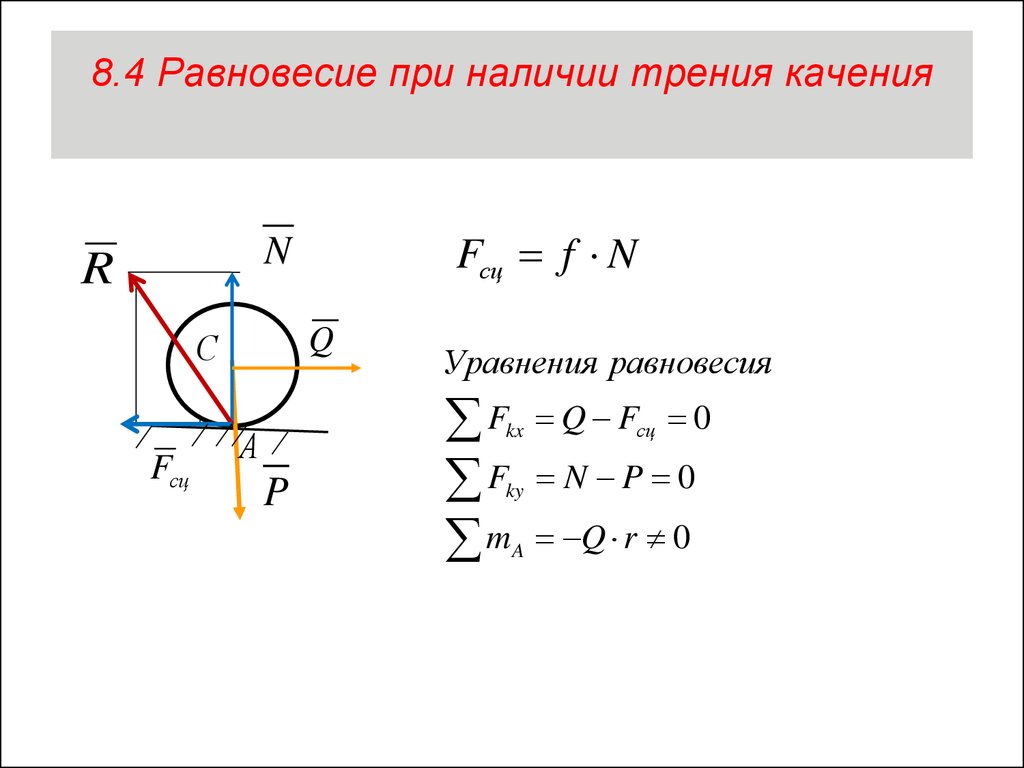
5. 8.4 Равновесие при наличии трения качения

Fсц f N
N
R
Q
С
Fсц
А
P
Уравнения равновесия
F
F
m
kx
Q Fсц 0
ky
N P 0
A
Q r 0

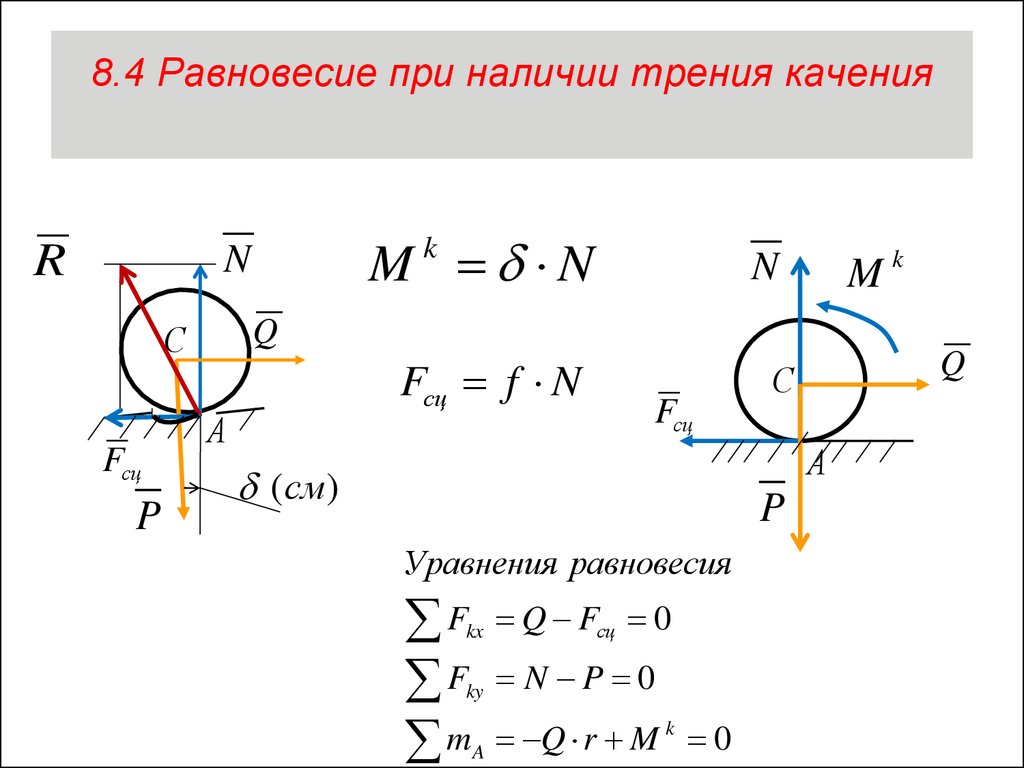
6. 8.4 Равновесие при наличии трения качения

R
M N
k
N
P
M
Q
С
Fсц
N
Fсц f N
А
Fсц
Q
С
А
(см )
P
Уравнения равновесия
F
F
m
kx
Q Fсц 0
ky
N P 0
A
Q r M k 0
k

7.

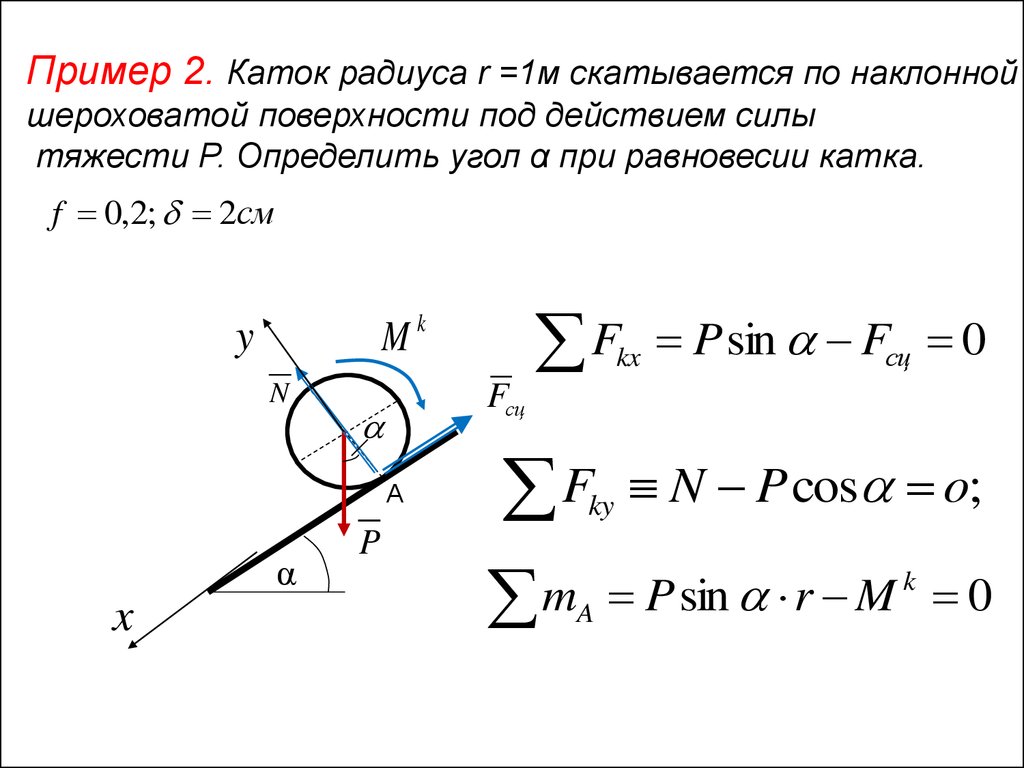
Пример 2. Каток радиуса r =1м скатывается по наклонной
шероховатой поверхности под действием силы
тяжести P. Определить угол α при равновесии катка.
f 0,2; 2см
N
α
P
kx
P sin Fсц 0
Fсц
A
x
F
Mk
y
F
ky
m
A
N P cos o;
P sin r M 0
k

8.

P sin Fсц 0 N P cos 0
k
Fсц fN
P sin r M 0
M k N
Fсц P sin
M k P sin r
N P cos ;
P sin fP cos
P sin r P cos
tg f ;
tg r
f 0,2
Различные состояния колеса в зависимости от угла
Равновесие
0
r
Качение без
скольжения
0,02
r
0,02
Качение со
скольжением
f 0,2
tg

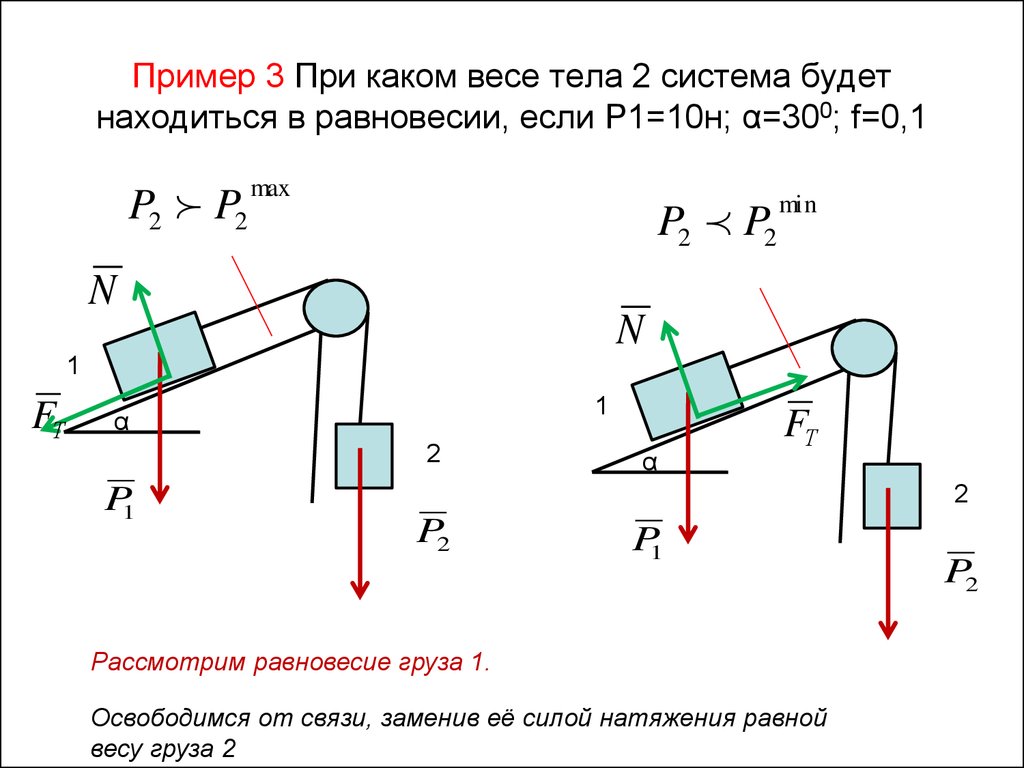
9. Пример 3 При каком весе тела 2 система будет находиться в равновесии, если P1=10н; α=300; f=0,1

P2 P2
max
P2 P2
min
N
N
1
FТ
1
α
2
P1
α
FТ
2
P2
P1
Рассмотрим равновесие груза 1.
Освободимся от связи, заменив её силой натяжения равной
весу груза 2
P2

10.

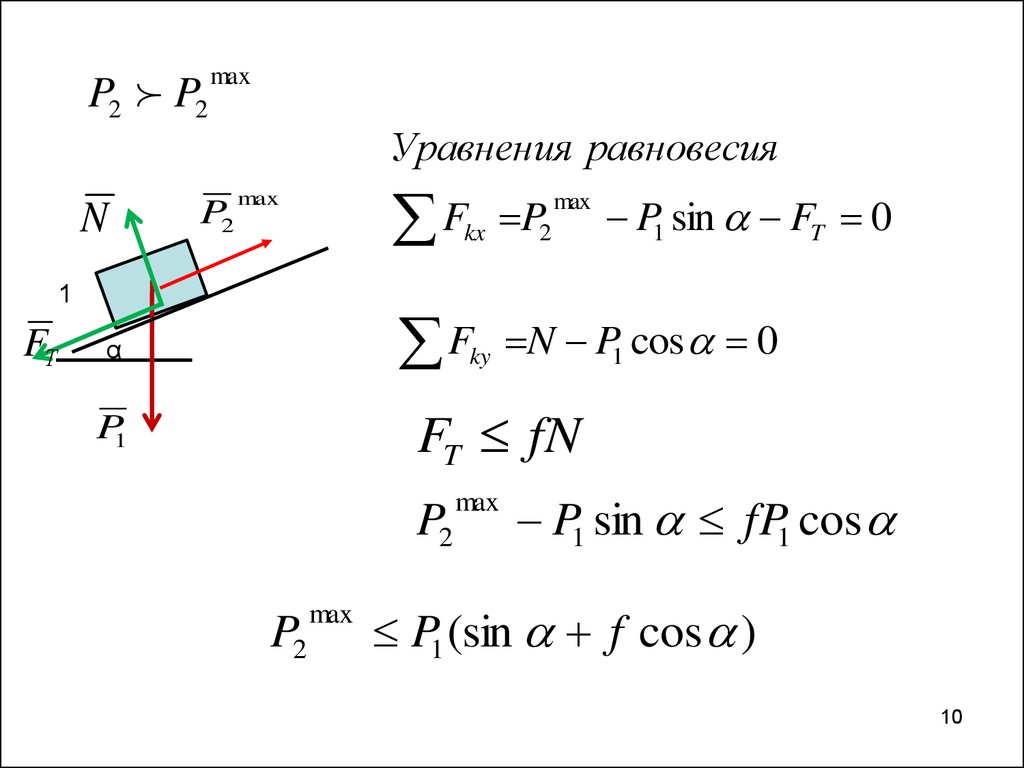
P2 P2
max
Уравнения равновесия
N
P2
F
max
kx
1
FТ
P2
F
α
ky
max
P1 sin FT 0
N P1 cos 0
FT fN
P1
P2
P2
max
max
P1 sin fP1 cos
P1 (sin f cos )
10

11.

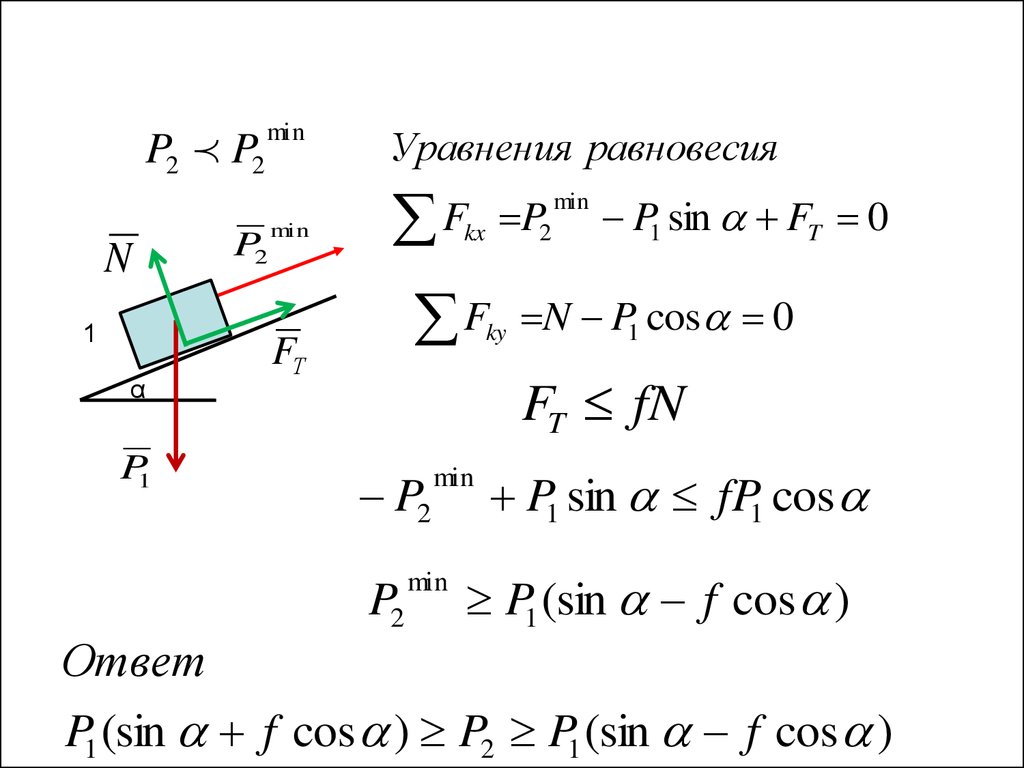
P2 P2
N
1
α
P1
min
P2
min
Уравнения равновесия
F
P2
kx
F
ky
FТ
min
P1 sin FT 0
N P1 cos 0
FT fN
P2
P2
min
min
P1 sin fP1 cos
P1 (sin f cos )
Ответ
P1 (sin f cos ) P2 P1 (sin f cos )