Предел последовательности и предел функции

1.

Предел последовательнос
ти и предел
функции

2.

Предел последовательн
ости
Рассмотрим две числовые последовательн
ости (уn) и (хn) и изобразим их члены точками
на координатной прямой.
(уn): 1, 3, 5, 7, 9,…, 2n – 1,…;
0 1
5
3
9
7
11
13
у
1111 1
, , , , ,...,
,...
(хn): 1
2345 n
0
1
12
1
6
1
4
1
3
1
2
1
х

3.

Обрати внимание, что члены последователь
ности (хn) как бы «сгущаются» около точки 0, а у
последовательности (уn) такой точки нет. В подоб
ных случаях говорят, что последовательность (хn
) сходится, а последовательность (уn) расходится
.
Чтобы узнать является ли конкретная точка,
взятая на прямой, «точкой сгущения» для членов
заданной последовательности, введем следующ
ее понятие.

4.

Определение 1. Пусть а – точка
прямой, а r – положительное число.
Интервал (а-r; a+r) называют окрест
ностью точки а, а число r – радиусо
м окрестности.
a-r
a
a+r
х
Пример. (3,97; 4,03) – окрестност
ь точки 4, радиус равен 0,03.

5.

В математике «точку сгущения» для ч
ленов заданной последовательности при
нято называть «пределом последователь
ности».
Определение 2. Число b называют
пределом последовательности (уn), ес
ли в любой заранее выбранной окрест
ности точки b содержатся все члены п
оследовательности, начиная с некотор
ого номера.
Обозначение: 1.
(уb
yn
n стремится к b или уn сходит
ся к b);
2.
y
b последовательности уn при стремлен
(предел
lim
n
n
ии n к бесконечности равен b)

6.

Примеры
1.
1
;0
lim
n
n
2. Если
Если
q ,1то
n
,1
то последовательность
q
ходится.
3.
n
q
; 0
lim
2
n
2
.
lim
n
n
1
n
q
рас

7.

Обсудим результаты, полученные в при
мерах с геометрической точки зрения. Для
этого построим графики последовательнос
тей:
1
yn ,
n
n
1
yn ,
2
2n
yn
.
n 1

8.

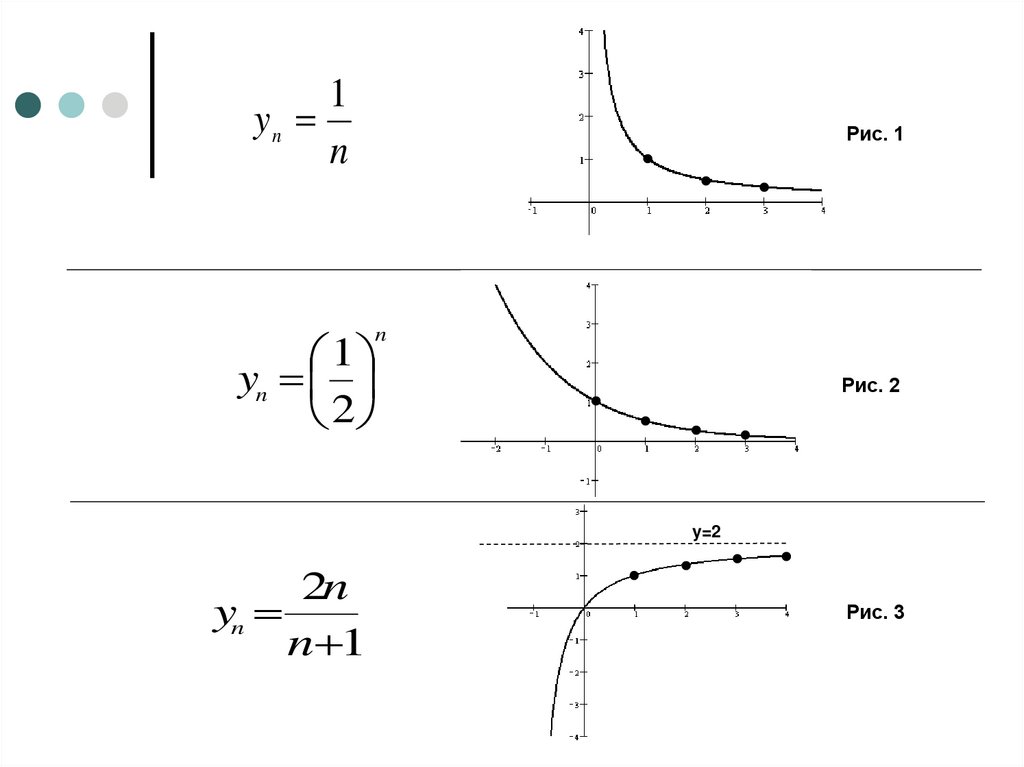
1
yn
n
yn
1
n
Рис. 1
n
1
yn
2
Рис. 2
y=2
2n
yn
n 1
Рис. 3

9.

Обрати внимание, что на всех трех рисун
ках точки графика, по мере их ухода вправо,
все ближе и ближе подходят к некоторой го
ризонтальной прямой:
на рис 1 – к прямой у=0,
на рис 2 – к прямой у=0,
на рис 3 – к прямой у=2.
Каждую из этих прямых называют горизо
нтальной асимптотой графика.

10.

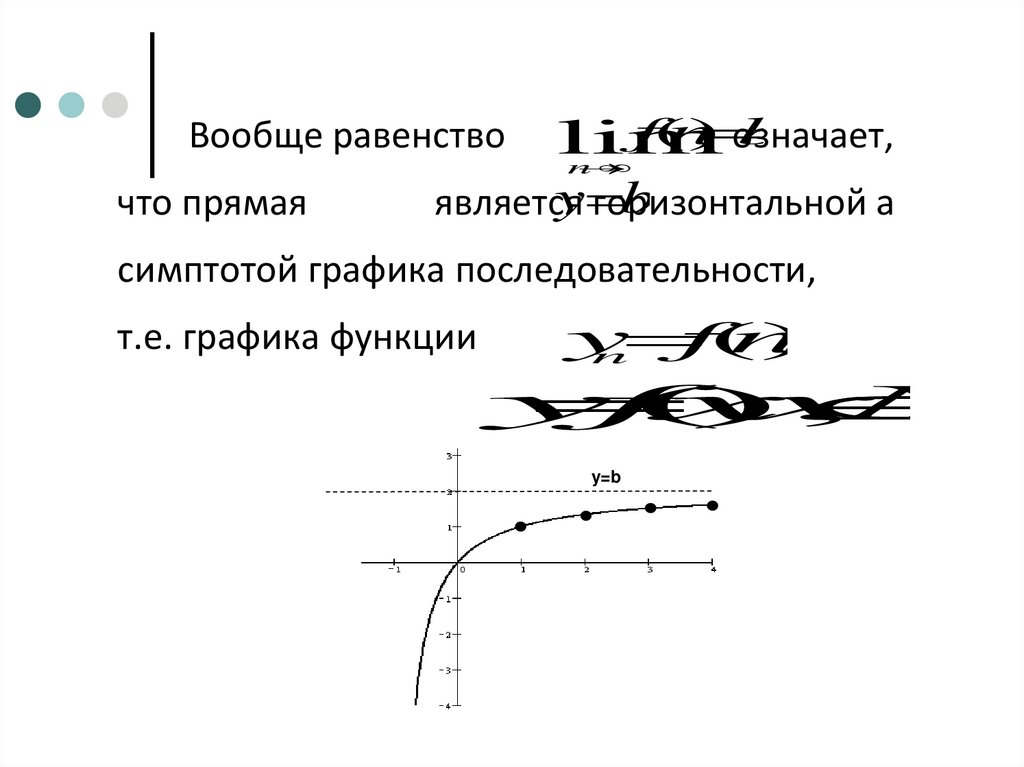
Вообще равенство
что прямая
f(n
)
b
означает,
lim
n
y
b
является
горизонтальной
а
симптотой графика последовательности,
т.е. графика функции
y
f(
n
)
n
y
f
(
x
),
x
N
.
y=b

11.

Свойства сходящихся п
оследовательностей
Свойство 1. Если последовательность
сходится, то только к одному пределу.
Свойство 2. Если последовательность
сходится, то она ограничена, обратное не
верно.
Свойство 3. Если последовательность
монотонна и ограниченна, то она сходитс
я.

12.

Вычисление пределов
последовательности
I. Предел стационарной последовате
льности равен значению любого члена п
оследовательности:
C C
lim
n

13.

y a
x b
Пусть lim
, lim
.
n
n
n
n
II. Предел суммы равен сумме преде
лов:
(
x
y
)
b
a
lim
n
Пример.
n
n

14.

III. Предел произведения равен произв
едению пределов:
(
x
y
)
b
a
lim
n
Пример.
n
n

15.

т
:
IV. Предел частного равен частному о
пределов
(при
условиях,
что
y
0
,
n
,
a
0
n
xn b
lim
y a
n
n
Пример.

16.

V. Постоянный множитель можно вы
нести за знак предела:
kx
kb
lim
n
Пример.
n

17.

Сумма бесконечной геометри
ческой прогрессии
Рассмотрим бесконечную геометрическую про
грессию
b
,
b
,
b
,
...,
b
,...
123
n
Вычислим суммы двух, трех и т.д. членов прог
рессии:
S1 b1 ;
S 2 b1 b2 ;
S 3 b1 b2 b3 ;
...
S n b1 b2 b3 ... bn ;
...

18.

Получилась последовательность
S
,
S
,
S
,
...,
S
,...
1 2 3
n
Она может сходиться или расходиться. Если после
довательность
сходится к пределу S, то число S
S
называется суммой геометрической прогрессии.
Ес
ли расходится, то о сумме геометрической прогрес
сии не говорят.
Формула суммы первых n членов геометрической
прогрессии следующая:
n
b1(qn 1)
Sn
q 1

19.

q
Теорема. Если знаменатель геометричес
кой прогрессии
нству
удовлетворяет
(bнераве
)
n
q 1 вы
, то сумма прогрессии
числяется по
S формуле
b1
S
1 q
Пример.

20.

Предел функции
1.
Предел функции на бесконеч
ности.
2.
Предел функции в точке.

21.

Предел функции на бес
конечности
Пусть дана функция
y
f(x
),
в области определения которой
содержится отрезок
;
,пусть прямая
и
y b
Является горизонтальной асимп
тотой графика функции
тогда
y
f(x
),
или
lim
f(x
)
b
x
lim
f(x
)
b
.
x
y=b

22.

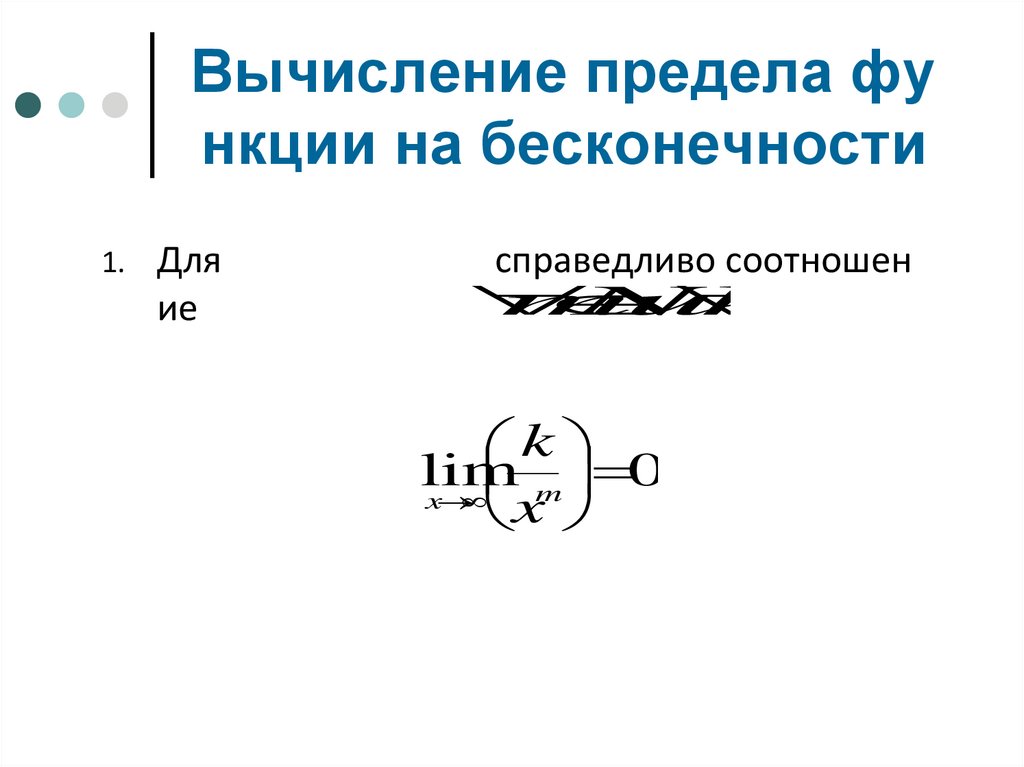
Вычисление предела фу
нкции на бесконечности
1.
Для
ие
справедливо соотношен
m
N
u
k
k
lim
0
m
x
x

23.

2. Если
g
(x
)
a ,то
f(x
)
b
, lim
lim
x
x
а) предел суммы равен сумме пределов:
(
f
(
x
)
g
(
x
))
b
a
lim
x
б) предел произведения равен произведению пре
делов:
(
f
(
x
)
g
(
x
))
b
a
lim
x

24.

в) предел частного равен частному от пределов:
f(x) b
lim
x
g
(x) a
г) постоянный множитель можно вынести за зн
ак предела:
kf
(
x
)
kb
lim
x
Пример.

25.

Предел функции в точк
е
Пусть дана функция
и пусть дана точка
y f(x
)
x
a
.
Пусть значение функции в это
й точке существует и равно т
огда b ,
y=f(x)
b
a
lim
f(x
)
b
.
x
a
(читают: предел функции
y
f(x
),
при стремлении х к а равен b)
Пример.

26.

Проверь себя!
Дорогой друг, теперь тебе предстоит п
роверить свои знания. Для этого нужно от
ветить на тест, который состоит из 10 воп
росов, К каждому вопросу дается на выбо
р три ответа, один из которых верный.
Желаю удачи!

27.

1. Окрестность какой точки явля
ется интервал (2,1; 2,3)?
а) 2;
б) 2,15;
в) 2,2.

28.

Неверно!
Попробуй еще!

29.

Верно!
Дальше!

30.

2. Интервал (7; 5) окрестность точ
ки 6, чему равен радиус этой ок
рестности?
а) 2;
б) 1;
в) 1,5.

31.

Неверно!
Попробуй еще!

32.

Верно!
Дальше!

33.

1
3. Последовательность yn
2n
является:
а) сходящейся;
б) расходящейся;
в) ничего определенного сказать не
льзя.

34.

Неверно!
Попробуй еще!

35.

Верно!
Дальше!

36.

4. Число b называют пределом п
оследовательности ( yn ) , ес
ли:
а) в любой окрестности точки b содержатся в
се члены последовательности, начиная с н
екоторого номера;
б) в любой окрес тности точки b содержатся
некоторые члены последовательности, нач
иная с некоторого номера;
в) в любой окрестности точки b не содержатс
я члены последовательности.

37.

Неверно!
Попробуй еще!

38.

Верно!
Дальше!

39.

f(n
)
b означает,
5. Равенство lim
n
что прямая y b является для
f(n
) :
графика y
n
а) горизонтальной асимптотой;
б) вертикальной асимптотой;
в) наклонной асимптотой.

40.

Неверно!
Попробуй еще!

41.

Верно!
Дальше!

42.

6. Какое из утверждений верно?
а) если последовательность имеет предел, т
о она монотонна;
б) если последовательность не монотонна, т
о она не имеет предела;
в) если последовательность ограничена, то о
на имеет предел.

43.

Неверно!
Попробуй еще!

44.

Верно!
Дальше!

45.

7. Предел последовательности
(
2
n
1
)(
n
3
) равен:
y
n
2
n
а) 0;
б) 1;
в) 2.

46.

Неверно!
Попробуй еще!

47.

Верно!
Дальше!

48.

8. Сумма геометрической прогрессии
1
равна:
27
,9
,3
,1
, ,...
3
а) 40;
б) 41;
в) 40,5.

49.

Неверно!
Попробуй еще!

50.

Верно!
Дальше!

51.

9. Найти
а) 0;
1
б) 1 ;
6
в) 2 1 .
6
7x 9
lim
:
x
6x 1

52.

Неверно!
Попробуй еще!

53.

Верно!
Дальше!

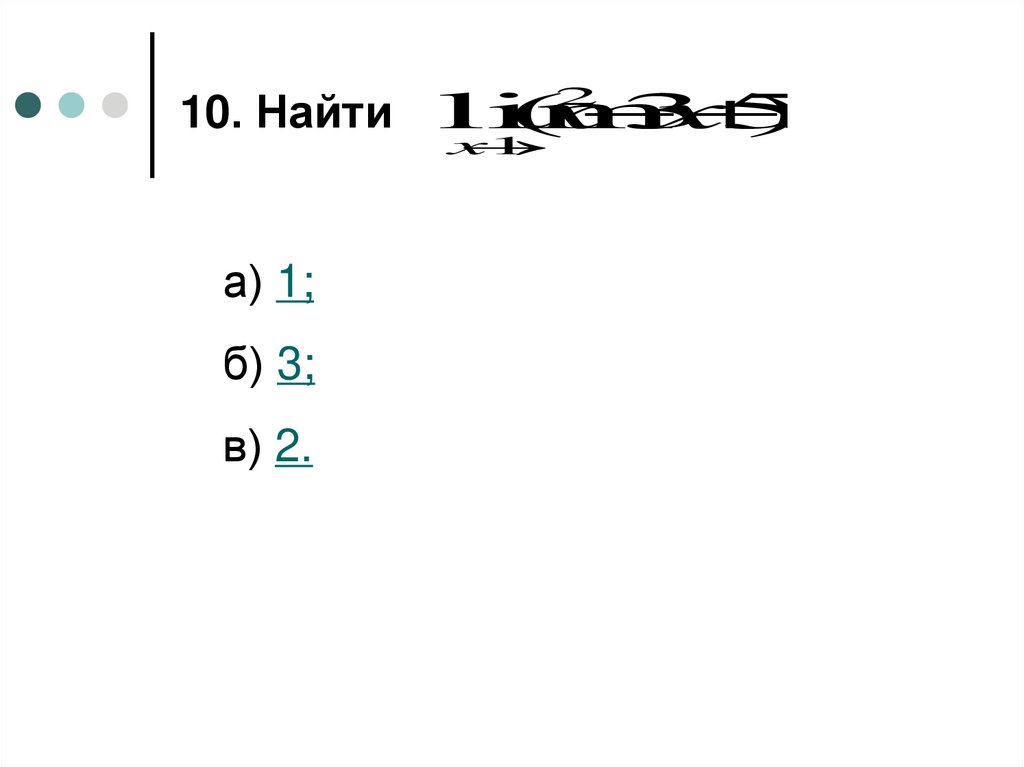
54.

10. Найти lim
(
x
3
x
5
)
:
2
x
1
а) 1;
б) 3;
в) 2.

55.

Неверно!
Попробуй еще!

56.

Верно!
Дальше!

57.

58.

Пример. Найти предел последовательности
1
yn 3.
n
Решение.
1
1
3
3
0
3
3
lim
lim
lim
n
n
n n
n

59.

Пример. Вычислить
2n2 1
.
lim
2
n
n
1
Решение. Делим числитель и знаменатель дроб
и почленно на наивысшую из имеющихся степен
ь переменной n, т.е. на n2.
2
2
n
1
1
2
2
2
2
2 2
2
n
1
02
n
n
n
2
2
lim
lim
lim
2
1
n1 n
n
n
1n
1
01
1
2
2
2
n
n
n

60.

Пример. Найти предел последовательности
1
yn 2
n
Решение.
1
1 1
0
0
0
lim
lim
2 lim
n
n
nn
n
n

61.

Пример. Найти предел последовательности
5
yn .
n
Решение.
5
1
1
5
5
5
0
0
lim
lim
lim
n
n
n
n
n
n

62.

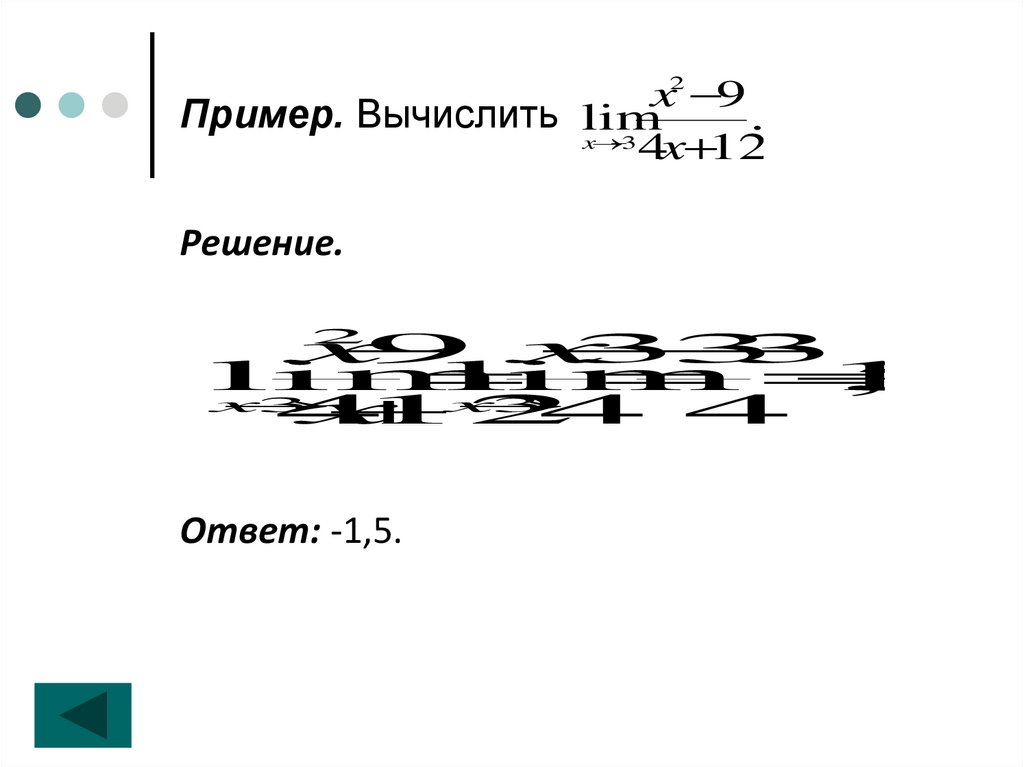
x2 9
Пример. Вычислить lim
.
x
3
4x 12
Решение.
2
x
9 x
3
3
3
lim
lim
1
,
5
.
x
3
x
3
4
x
12
4 4
Ответ: -1,5.

63.

Дано (уn)=
1111 1
1
, , , , ,
...,
,...
2345 n
Доказать, что
1
0
lim
n
n
Решение. Возьмем любую окрестность точки 0, с
радиусом r. Подберем натуральное число n0 так, чтоб
1
r
ы выполнялось неравенство
n
Если например, r=0,001, то в качестве n0 можно в
3
зять 1001; если
, то nr0=5774.
5774
Член данной последовательности с номером n0 п
опадает в выбранную окрестность точки 0. В этой же о
крестности будут находиться все последующие члены,
тогда по определению 2 следует, что
1
0
lim
n n

64.

Пример. Найти сумму геометрической п
рогрессии
Решение. Здесь
11
4
,2
,1
, , ,...
24
1
b
4, q Так
. как знаменатель
1
2
прогрессии удовлетворяет неравенству
воспользовавшись
q формулой
1,
b1
S
1 q
Ответ:
S 8
.
4
S
8
1
1
2
, то
, получим

65.

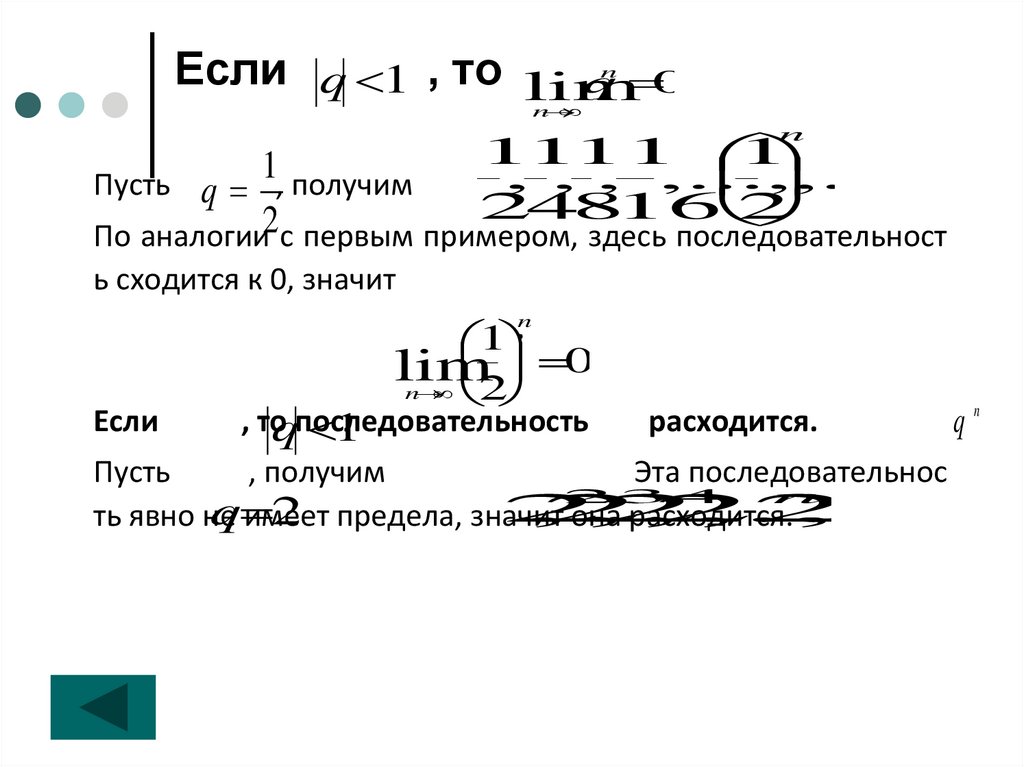
Если q 1 , то lim
q 0
n
n
n
1111 1
1
, , , ,...,
,...
Пусть q , получим
24816 2
2
По аналогии с первым примером, здесь последовательност
ь сходится к 0, значит
n
.
1
0
lim
2
n
Если
, тоqпоследовательность
1
расходится.
qn
Пусть
, получим
Эта последовательнос
234
n
2
,
2
,
2
,
2
,...,
2
q
2 предела, значит она расходится.,...
ть явно не
имеет

66.

Дана последовательность
2468 2
n
, , , ,...,,.
2345 n
1
найти ее предел.
Выполним некоторые преобразования выражения
2n
:
n 1
2
n
2
n
2
2
2
(
n
1
)
2
(
n
1
)
2 2
2
n
1
n
1
n
1
n
1
n
1
n
1
Это значит, в частности, что
8
2
6
2
2 и т. д.,
2
;
4
3 1 5
4 1
2
2 4
2
2
; 2
;
2
1 1 3
2 1
Данную последовательность перепишем так:
2222
2
2
,
2
,
2
,
2
,
...,
2
,...
2345 n
1
Видно, что «точкой сгущения» является 2, значит
2n
2
lim
n
n
1

67.

Рассмотрим пример.
Дана последовательность (хn)=1
, 2, 3, 1, 2, 3,…, 1, 2, 3,…. Эта пос
ледовательность ограничена, но
не является сходящейся.

68.

Пример. Вычислить
2x2 3
2 .
lim
x
x4
Решение. Разделим числитель и знаменатель др
оби почленно на х2:
2
2
x
3
3
2
2
2
2
2 2
2
x
3
02
x
x
x
2
2
lim
lim
lim
2
41
x
x 4 n
x
4n
01
1
2
2
2
x
xx
Ответ: 2.