Моделирование процессов и объектов в производственных системах

1. Моделирование процессов и объектов в производственных системах

Чинахов Дмитрий Анатольевич
СибГИУ - 2022

2.

Модель – это такой материальный или мысленно представляемый объект, который
в процессе познания (изучения) замещает объект-оригинал, сохраняя некоторые
важные для данного исследования типичные его черты.
Модель нужна:
1) для того чтобы понять как устроен конкретный объект; какова его структура,
основные свойства законы развития и взаимодействия с окружающим миром;
2) для того чтобы научиться управлять объектом (или процессом) и определить
наилучшие способы управления при заданных целях и критериях;
3) для того чтобы прогнозировать прямые и косвенные последствия реализации
заданных способов и форм воздействия на объект.
Хорошо построенная модель, как правило, обладает удивительным свойством: ее
изучение дает некоторые новые звания об объекте – оригинале.
2

3.

Процесс построения модели называется моделированием.
Существует несколько приемов моделирования, которые можно условно объединить в две
большие группы: материальное (предметное) и идеальное моделирование.
К материальным относятся такие способы моделирования, при которых исследование ведется на
основе модели, воспроизводящей основные геометрические, физические, динамические и
функциональные характеристики изучаемого объекта. Основными разновидностями
материального моделирования являются физические и аналоговые моделирования.
Физическим принято называть моделирование, при котором реальному объекту
противопоставляется его увеличенная или уменьшенная копия, допускающая исследование (как
правило, в лабораторных условиях) с помощью последующего перенесения свойств изучаемых
процессов и явлений с модели на объект на основе теории подобия. Примеры: в астрономии –
планетарий, в гидротехнике – лотки с водой, моделирующие реки и водоемы, в архитектуре –
макеты зданий, в самолетостроении – модели летательных аппаратов и т. п.
Аналоговое моделирование основано на аналогии процессов и явлений, имеющих различную
физическую природу, но одинаково описываемых формально (одними и теми же математическими
уравнениями, логическими схемами и т. п.). Наиболее простой пример – изучение механических
колебаний с помощью электрической схемы, описываемой теми же дифференциальными
уравнениями.
3

4.

Идеальное моделирование носит теоретический характер.
Различают два типа идеального моделирования: интуитивное и знаковое.
Под интуитивным понимаем моделирование, основанное на интуитивном
представлении об объекте исследования, не поддающемся формализации либо не
нуждающемся в ней. Например, жизненный опыт каждого человека может
считаться его интуитивной моделью окружающего мира.
Знаковым называется моделирование, использующее в качестве моделей знаковые
преобразования какого-либо вида: схемы, графики, чертежи, формулы, наборы
символов и т.д., а также включающее совокупность законов, по которым можно
оперировать с выбранными знаковыми образованьями и их элементами.
Важнейшим видом знакового моделирования является математическое
моделирование, при котором исследование объекта осуществляется посредством
модели, сформулированной на языке математики, и использованием тех или иных
математических
методов.
Классическим
примером
математического
моделирования является описание и исследование основных законов механики И.
Ньютона средствами математики.
4

5.

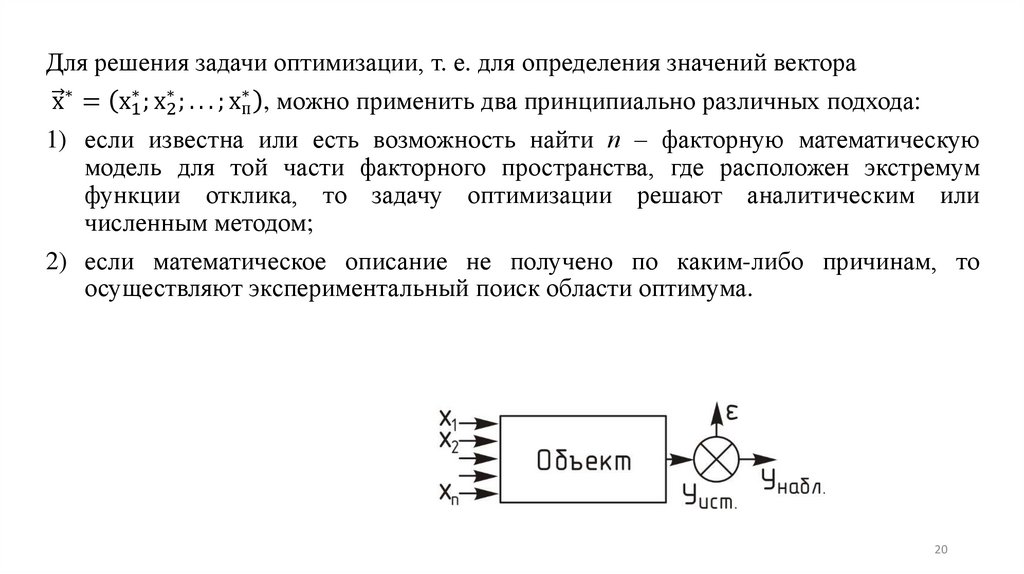
Основные виды математических моделей:
-Дескриптивные модели
-Оптимизационные модели
(mах Ф(u) = Ф(u)), u ∈ U
либо (min Ф(u) = Ф(u)), u ∈ U
-Многокритериальные модели (Сведение двух критериев к одному, Метод
последовательных уступок)
-Игровые модели
-Имитационное моделирование
Имитационное моделирование – методология экспериментально-теоретического
решения технических задач управления сложной Технологической системой.
5

6.

Под математическим моделированием понимают изучение свойств объекта на
математической модели. Его целью является определение оптимальных условий
протекания процесса, управление им на основе математической модели и перенос
результатов на объект.
Математической моделью называется приближенное описание какого-либо явления
или процесса внешнего мира, выраженное с помощью математической символики.
Математическое моделирование включает три взаимосвязанных этапа:
1) составление математического описания изучаемого объекта;
2) выбор метода решения системы уравнений математического описания и
реализация его в форме моделирующей программы;
3) установление соответствия (адекватности) модели объекту.
При построении математической модели реальное явление упрощается, схематизируется и полученная
схема описывается в зависимости от сложности явлений с помощью того или иного математического
аппарата.
При построении математических моделей широко используют блочный принцип, суть которого состоит
в том, что модель строится из отдельных логически законченных блоков, отражающих обычно ту или
иную сторону рассматриваемого процесса.
6

7.

Цель и задача о приближении (аппроксимации) функций: данную
функцию
f(х)
требуется
приближенно
заменить
(аппроксимировать) некоторой функцией (х) так, чтобы
отклонение (в некотором смысле) (х) от f(x) в заданной области
было наименьшим. Функция (х) при этом называется
аппроксимирующей.
Аппроксимации функции многочленом (х) = а0 + а1х + а2х2 + … + аmхm
*
Одним из основных типов точечной аппроксимации является
интерполирование. Оно состоит в следующем: для данной
функции у = f(x) строим многочлен (*), принимающий в заданных
точках хi, те же значения уi, что и функция f(х).
Цель и задача функции интерполирования: данную функцию f(х)
требуется приближенно заменить (интерполировать) некоторой
функцией (х), проходящую через выбранные узловые точки, так,
чтобы отклонение (в межузловых точках) (х) от f(x) в заданной
области было наименьшим. Функция (х) при этом называется
интерполирующей.
Методы делят на глобальную и локальную интерполяцию.
Рис. Интерполяция и
аппроксимация
7

8.

Исходом любого опыта (испытания), осуществляемого при вполне определенных
условиях, является событие. Событие может иметь качественную или
количественную характеристику.
События бывают достоверные, невозможные и случайные.
Степенью возможности реализации случайного события является вероятность. Если
опыт сводится к схеме случаев, то под вероятностью события А понимают отношение
числа случаев, благоприятных данному событию, к общему числу всех несовместимых
единственно возможных и равновозможных случаев: