Взаимное расположение прямой и окружности

1.

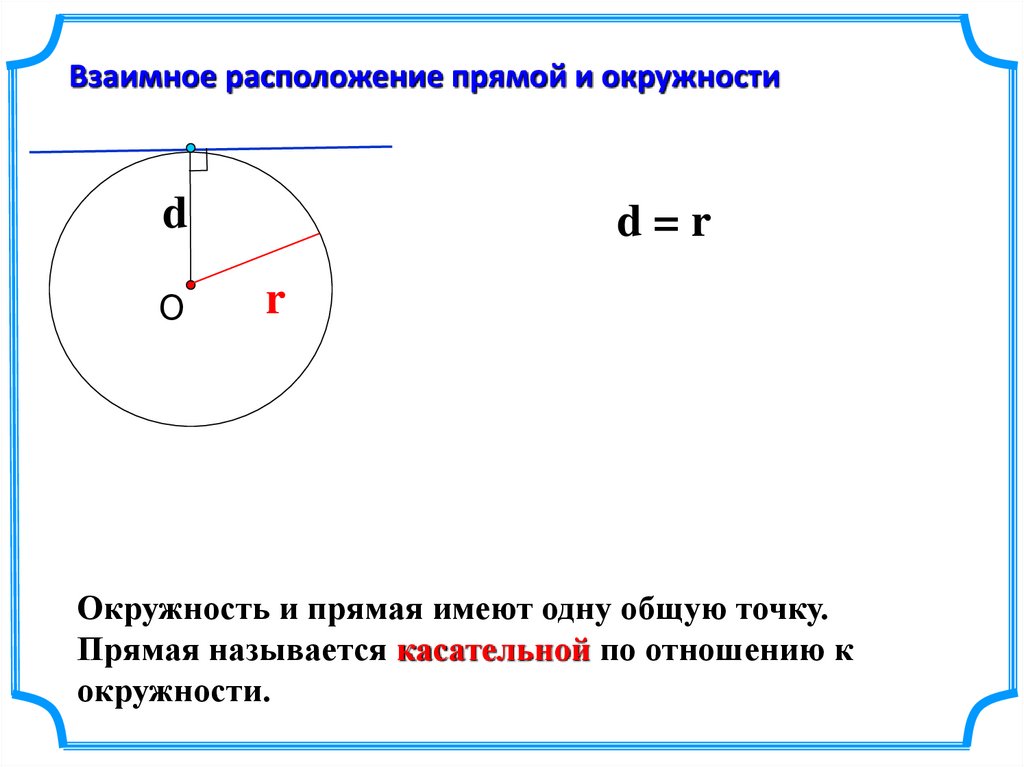
Взаимное расположение прямой и окружности
d
О
d=r
r
Окружность и прямая имеют одну общую точку.
Прямая называется касательной по отношению к
окружности.

2.

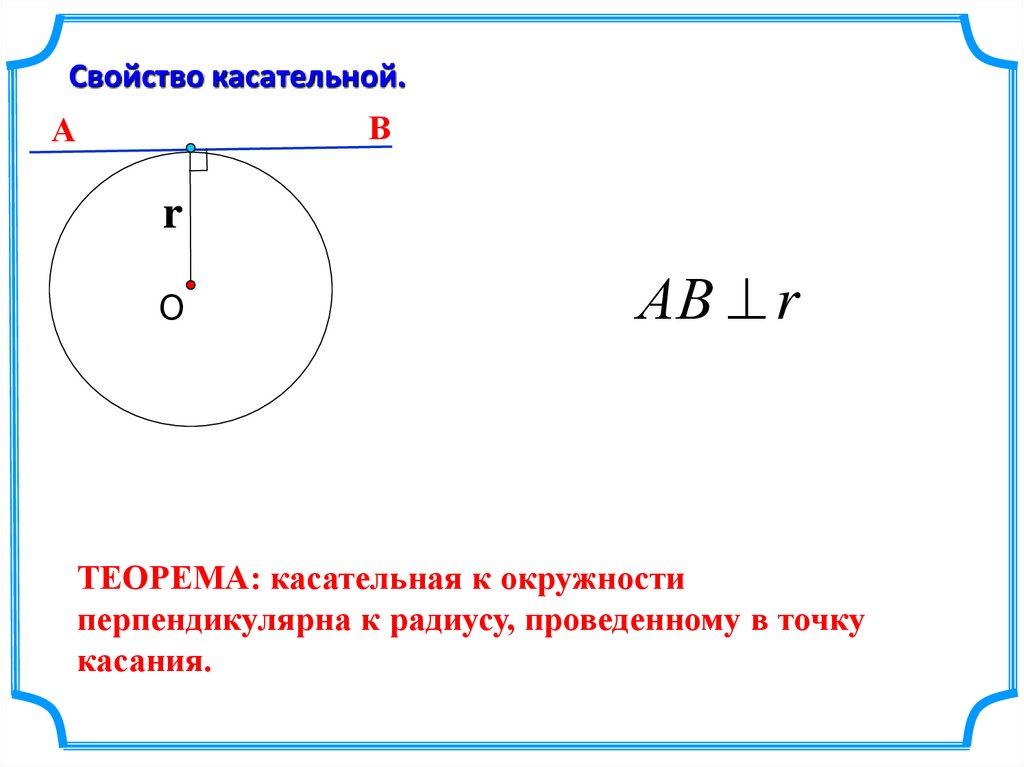
Свойство касательной.
В
А
r
О
АВ r
ТЕОРЕМА: касательная к окружности
перпендикулярна к радиусу, проведенному в точку
касания.

3.

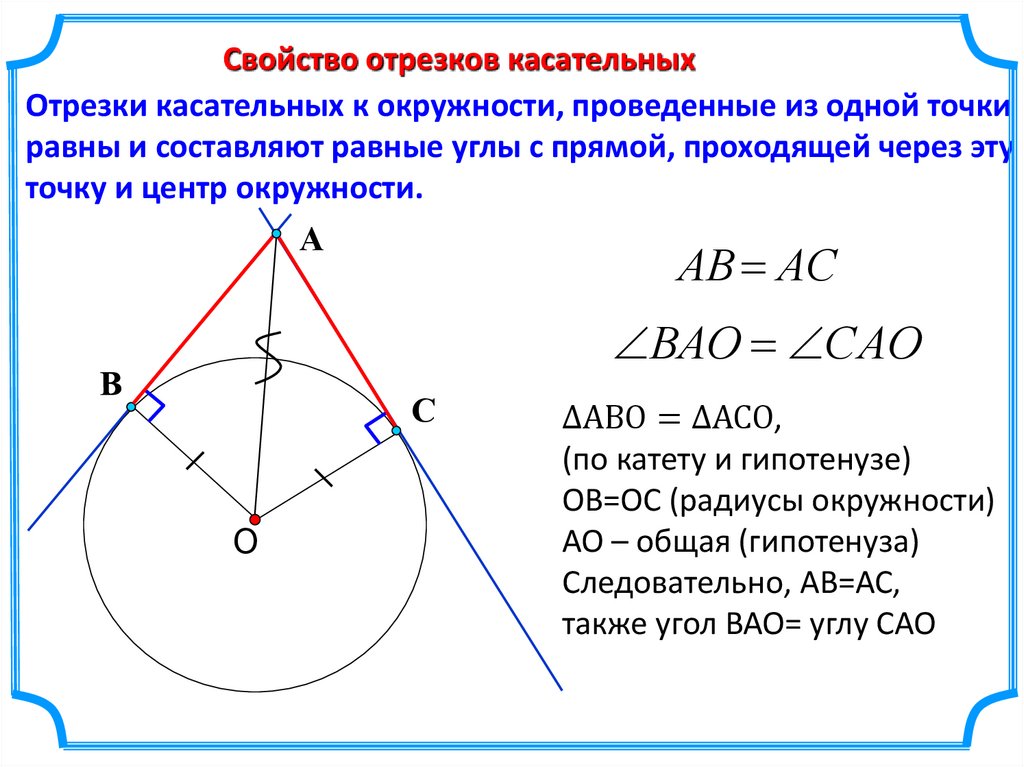
Свойство отрезков касательных
Отрезки касательных к окружности, проведенные из одной точки
равны и составляют равные углы с прямой, проходящей через эту
точку и центр окружности.
А
АВ АС
ВАО САО
С
О
∆АВО = ∆АСО,
(по катету и гипотенузе)
ОВ=ОС (радиусы окружности)
АО – общая (гипотенуза)
Следовательно, АВ=АС,
также угол ВАО= углу САО

4.

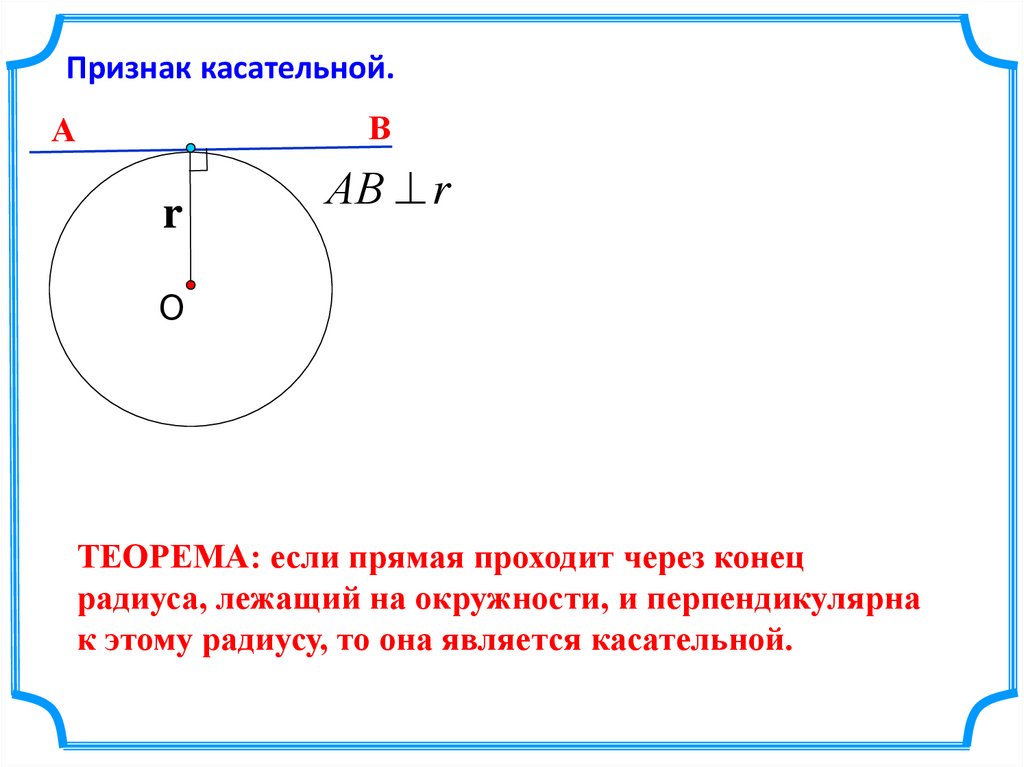
Признак касательной.
В
А
r
АВ r
О
ТЕОРЕМА: если прямая проходит через конец
радиуса, лежащий на окружности, и перпендикулярна
к этому радиусу, то она является касательной.

5.

6.

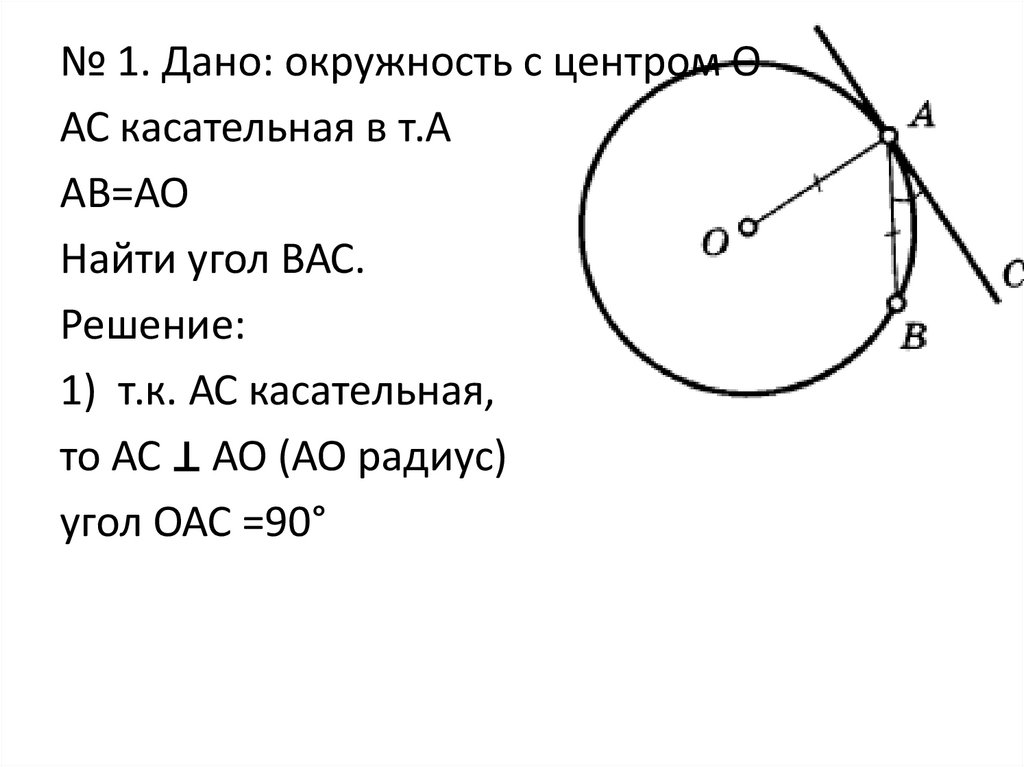
№ 1. Дано: окружность с центром О
АС касательная в т.А
АВ=АО
Найти угол ВАС.
Решение:
1) т.к. АС касательная,
то АС ⊥ АО (АО радиус)
угол ОАС =90°

7.

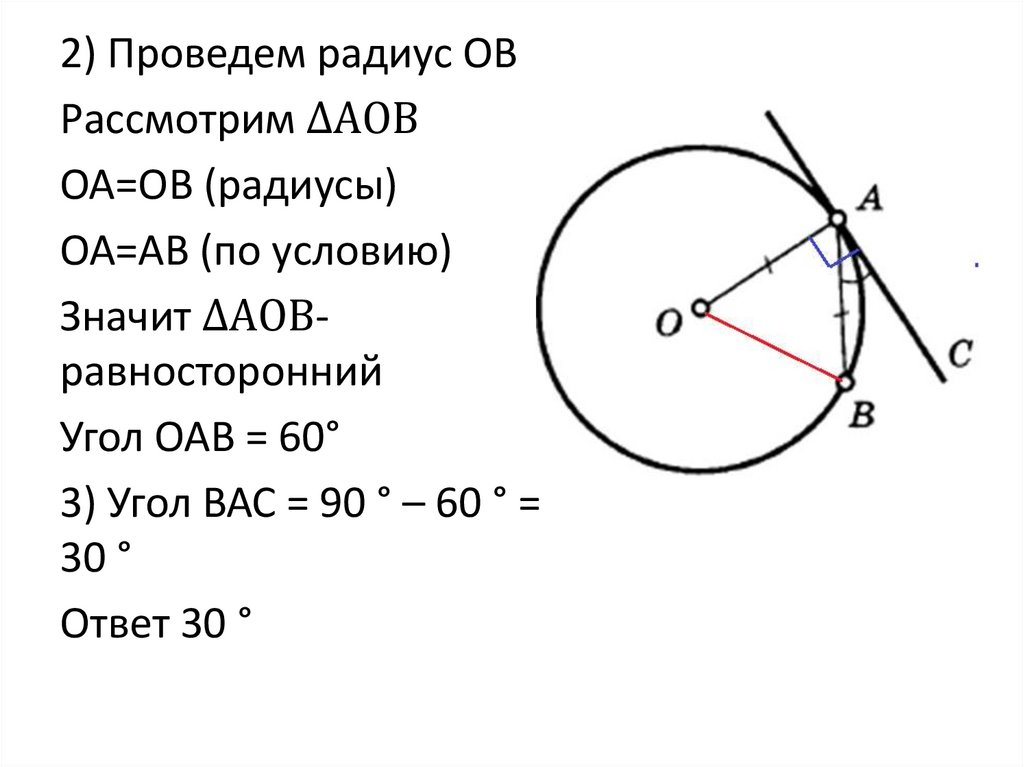
2) Проведем радиус ОВ
Рассмотрим ∆АОВ
ОА=ОВ (радиусы)
ОА=АВ (по условию)
Значит ∆АОВравносторонний
Угол ОАВ = 60°
3) Угол ВАС = 90 ° – 60 ° =
30 °
Ответ 30 °

8.

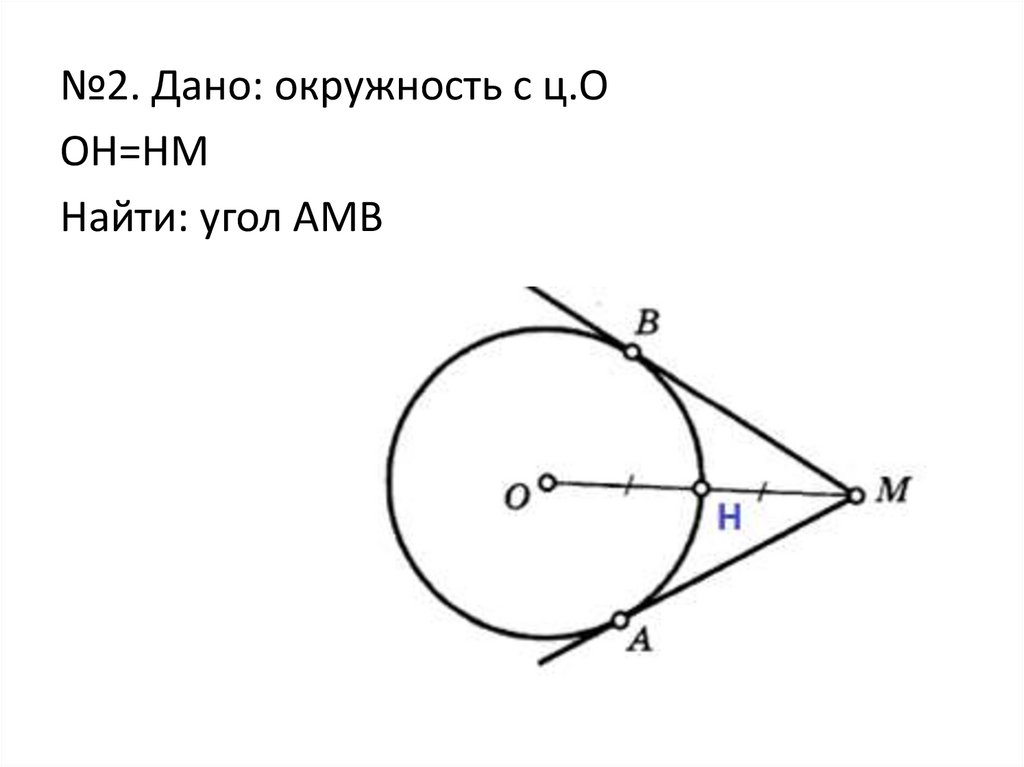
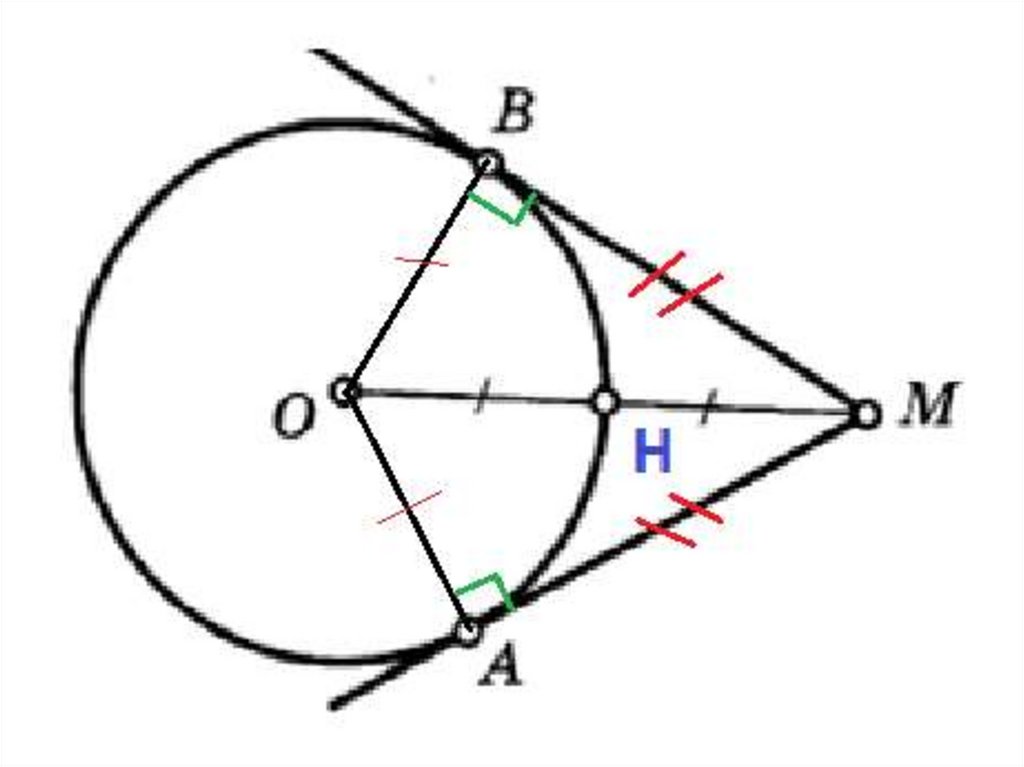
№2. Дано: окружность с ц.О
ОН=НМ
Найти: угол АМВ

9.

10.

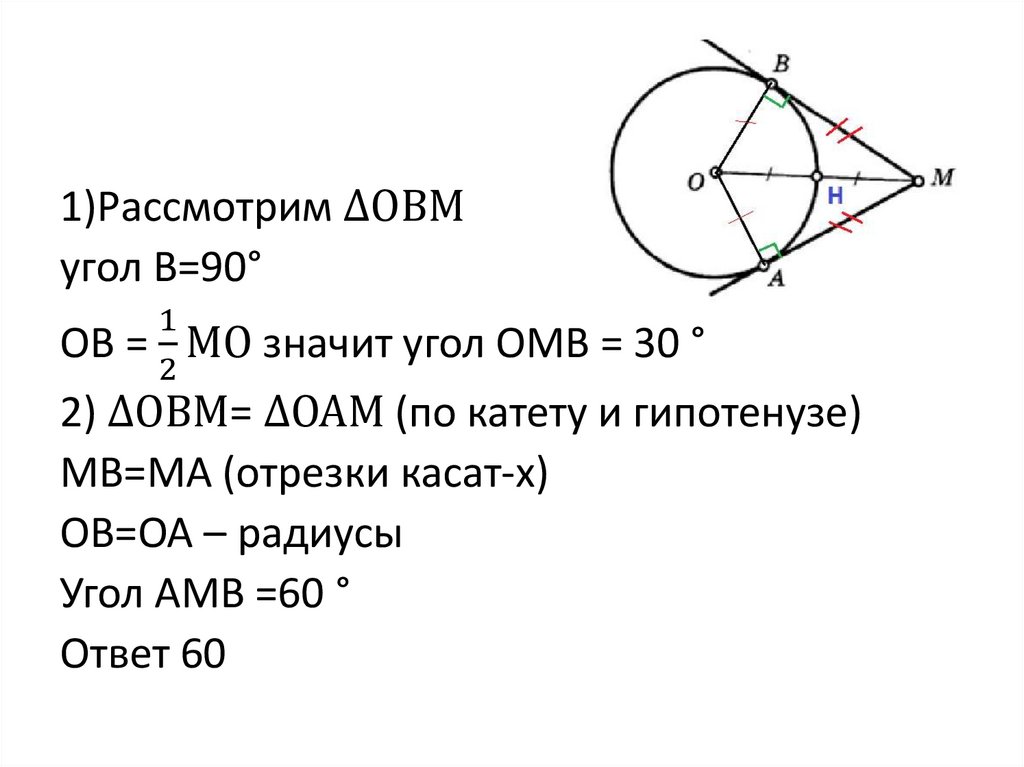
1)Рассмотрим ∆ОВМ
угол В=90°
ОВ =
1
МО
2
значит угол ОМВ = 30 °
2) ∆ОВМ= ∆ОАМ (по катету и гипотенузе)
МВ=МА (отрезки касат-х)
ОВ=ОА – радиусы
Угол АМВ =60 °
Ответ 60

11.

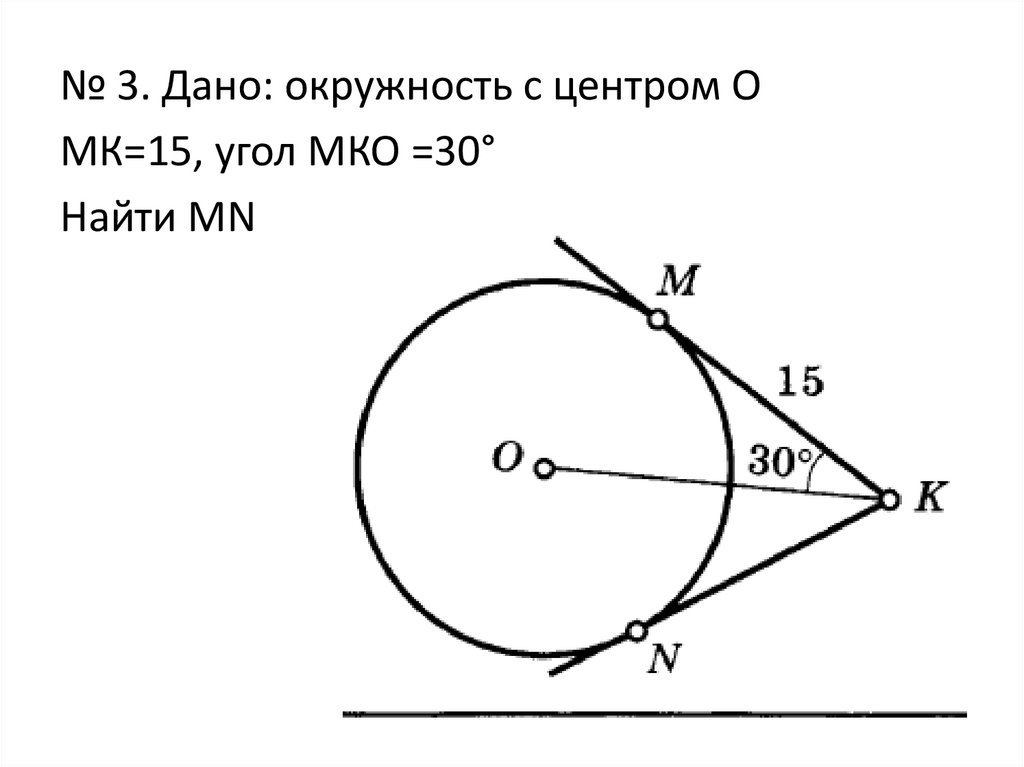
№ 3. Дано: окружность с центром О
МК=15, угол МКО =30°
Найти МN

12.

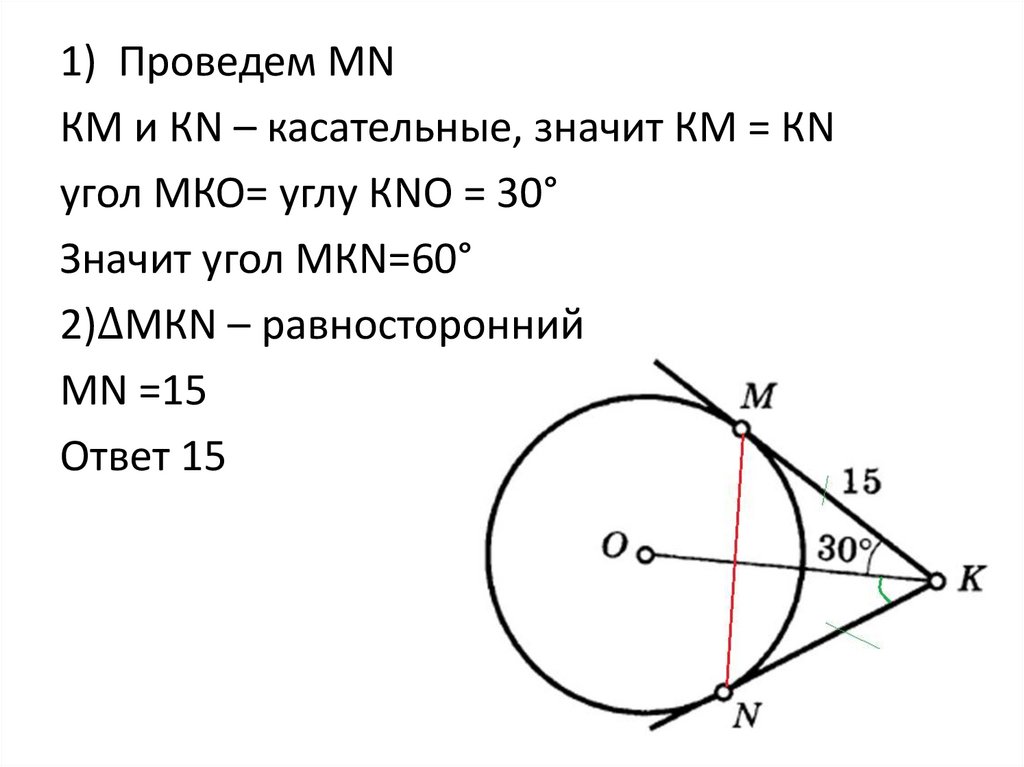
1) Проведем МN
КМ и КN – касательные, значит КМ = КN
угол МКО= углу КNО = 30°
Значит угол МКN=60°
2)∆МКN – равносторонний
МN =15
Ответ 15

13. № 4

№4

14.

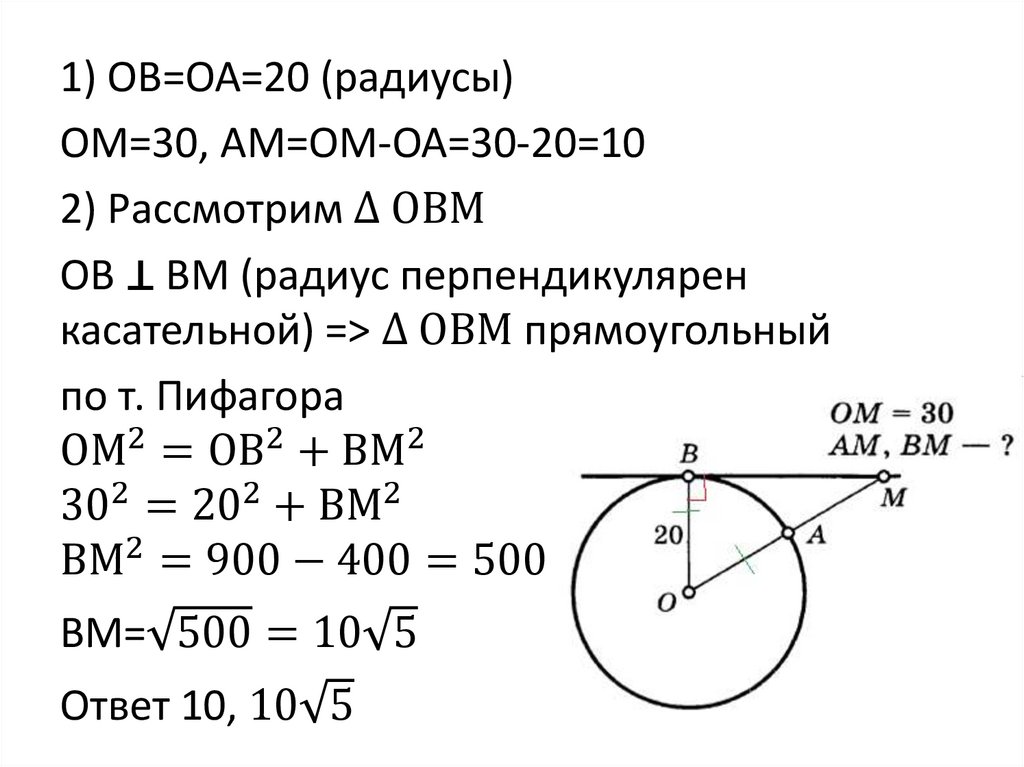
1) ОВ=ОА=20 (радиусы)
ОМ=30, АМ=ОМ-ОА=30-20=10
2) Рассмотрим ∆ ОВМ
ОВ ⊥ ВМ (радиус перпендикулярен
касательной) => ∆ ОВМ прямоугольный
по т. Пифагора
ОМ2 = ОВ2 + ВМ2
302 = 202 + ВМ2
ВМ2 = 900 − 400 = 500
ВМ= 500 = 10 5
Ответ 10, 10 5

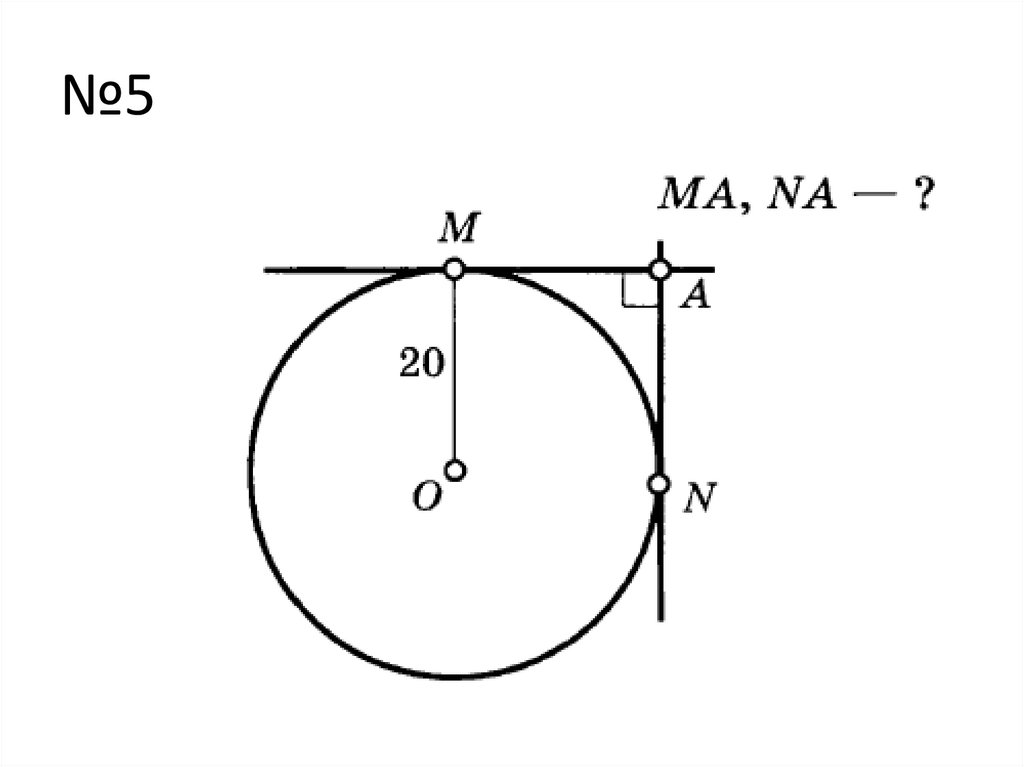
15. №5

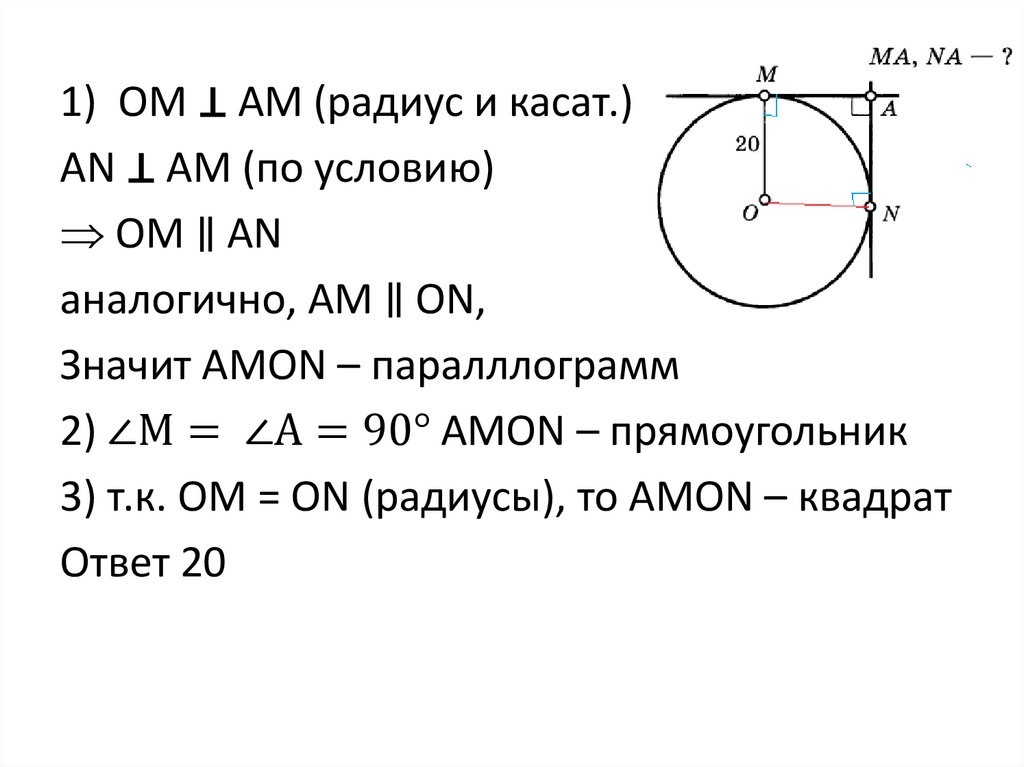
16.

1) ОМ ⊥ АМ (радиус и касат.)
AN ⊥ AM (по условию)
ОМ ∥ АN
аналогично, АМ ∥ ОN,
Значит АМОN – паралллограмм
2) ∠М = ∠А = 90° АМОN – прямоугольник
3) т.к. ОМ = ОN (радиусы), то АМОN – квадрат
Ответ 20

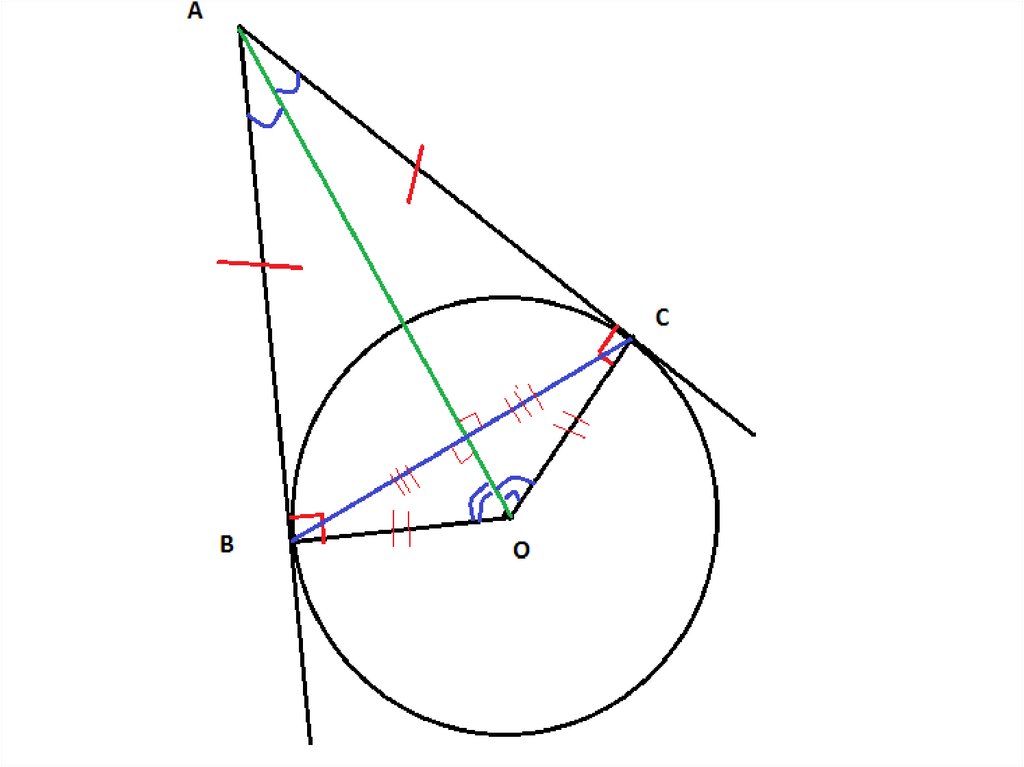
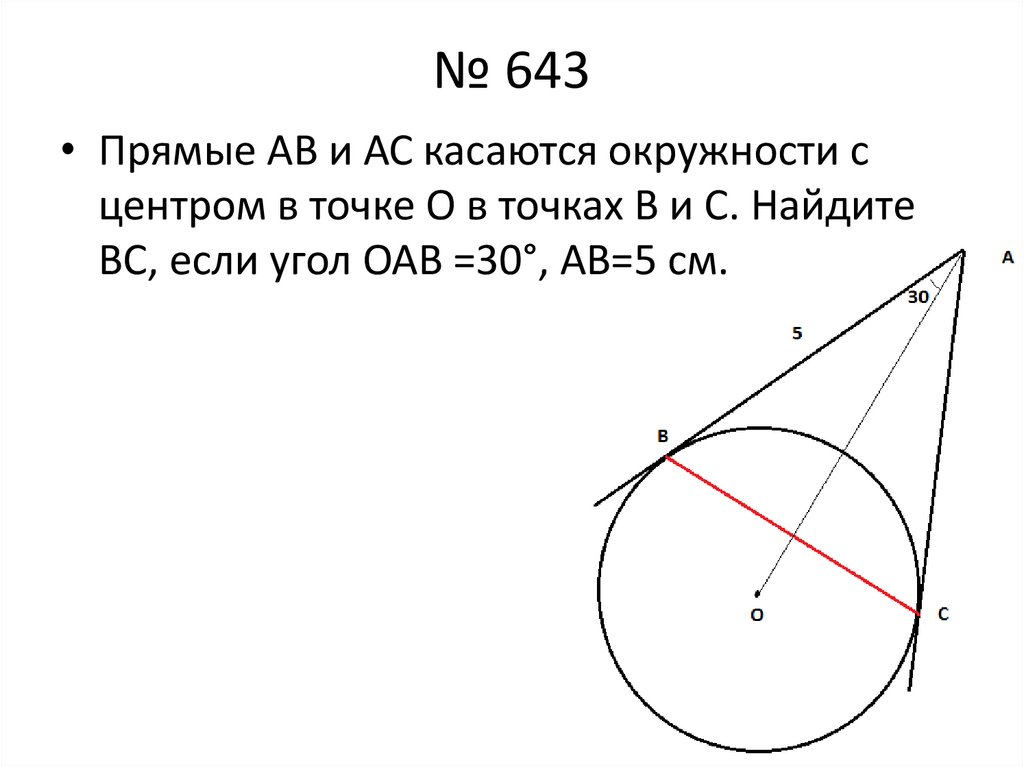
17. № 643

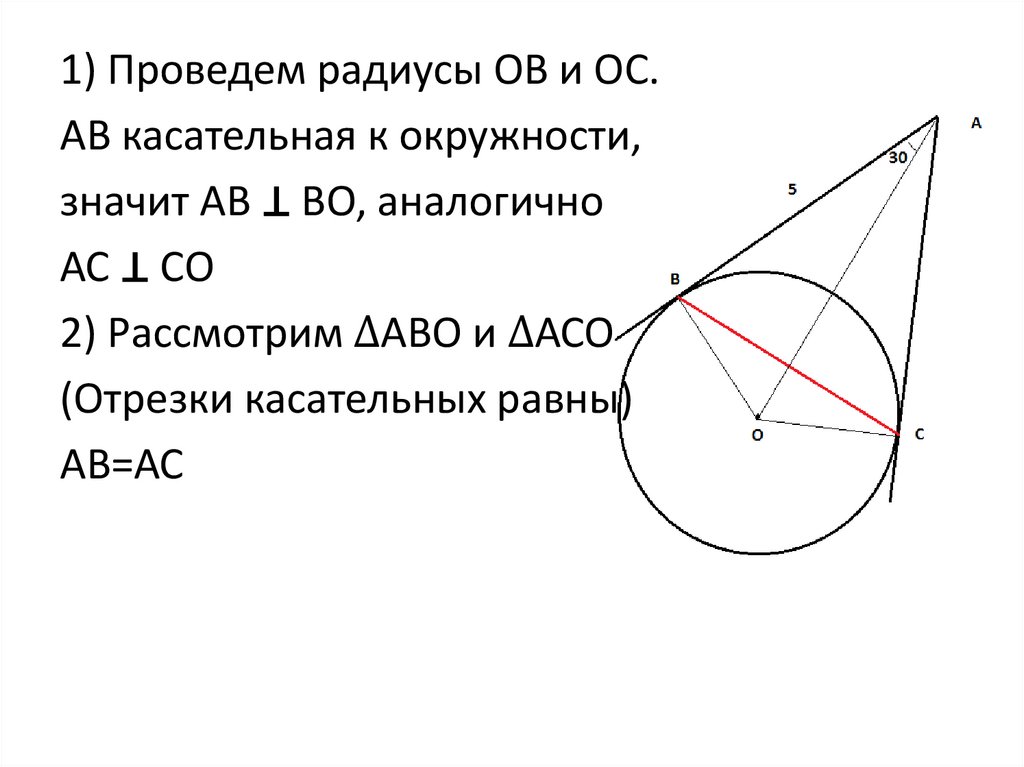
• Прямые АВ и АС касаются окружности с
центром в точке О в точках В и С. Найдите
ВС, если угол ОАВ =30°, АВ=5 см.

18.

1) Проведем радиусы ОВ и ОС.
АВ касательная к окружности,
значит АВ ⊥ ВО, аналогично
АС ⊥ СО
2) Рассмотрим ∆АВО и ∆АСО
(Отрезки касательных равны)
АВ=АС

19.

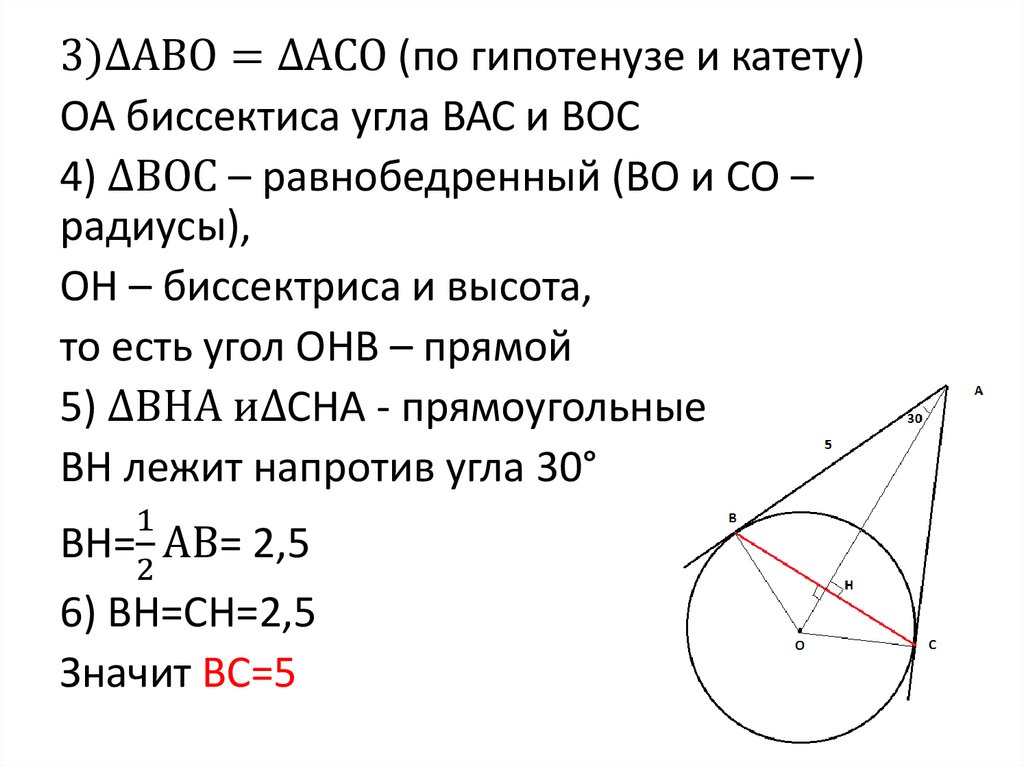
3)∆АВО = ∆АСО (по гипотенузе и катету)
ОА биссектиса угла ВАС и ВОС
4) ∆ВОС – равнобедренный (ВО и СО –
радиусы),
ОН – биссектриса и высота,
то есть угол ОНВ – прямой
5) ∆ВНА и∆СНА - прямоугольные
ВН лежит напротив угла 30°
1
ВН= АВ=
2
2,5
6) ВН=СН=2,5
Значит ВС=5

20.

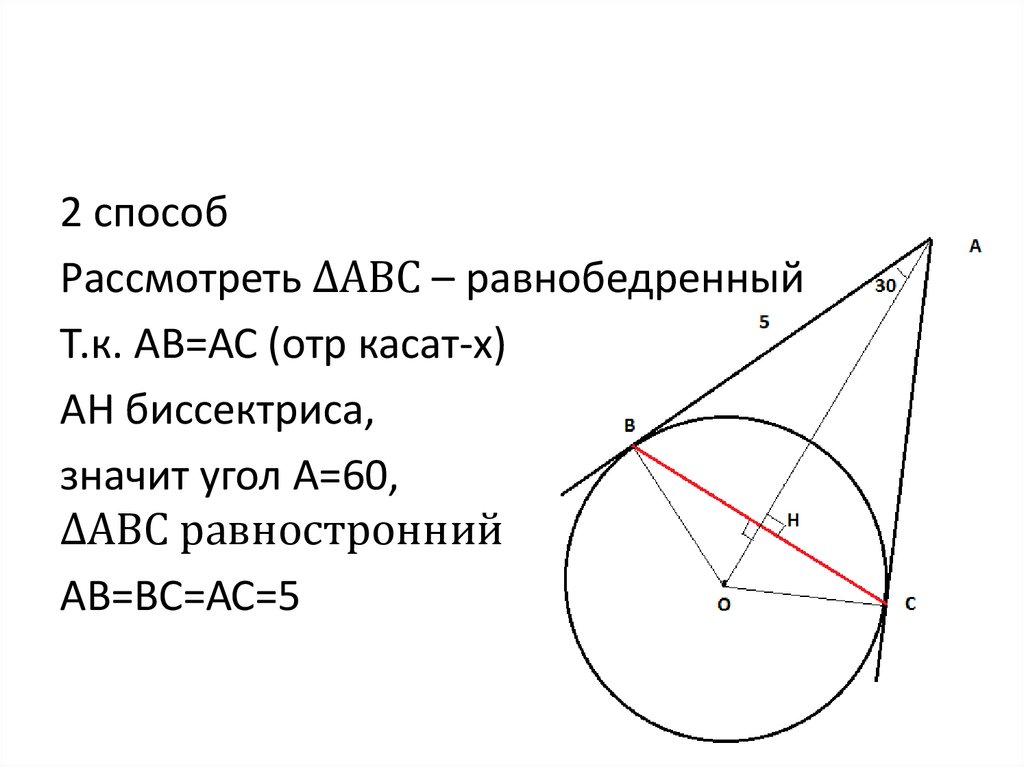
2 способ
Рассмотреть ∆АВС – равнобедренный
Т.к. АВ=АС (отр касат-х)
АН биссектриса,
значит угол А=60,
∆АВС равностронний
АВ=ВС=АС=5