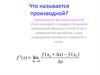Производная сложной функции

1. Производная сложной функции

2. Формулы дифференцирования

1. (хр)′=р·хр-1
1.1.(с)'=0, где с – число
1.2. (х)'=1
2. (ех)′=ех
1
3. (lnx)′= х , х>0
4. (sinx)′=cosx
5. (cosx)′=-sinx
6. (ах)′=ахlnx
7. (logax)′= 1
х ln a

3. Формулы дифференцирования

U – сложная функция
1. (uр)′=р·uр-1 ∙(u)`
2. (еu)′=еu ∙(u)`
(u)
3. (lnu)′=
u
4. (sinu)′=cosu ∙(u)`
5. (cosu)′=-sinu ∙(u)`
6. (аu)′=аulnu ∙(u)`
7. (logau)′= (u )
u ln a

4. Формулы дифференцирования

Х – простая функция
1. (хр)′=р·хр-1
1.1.(с)'=0, где с – число
1.2. (х)'=1
2. (ех)′=ех 1
3. (lnx)′= х , х>0
4. (sinx)′=cosx
5. (cosx)′=-sinx
6. (ах)′=ахlnx
1
7. (logax)′=
х ln a
U – сложная функция
1. (uр)′=р·uр-1 ∙(u)`
2. (еu)′=еu ∙(u)`
(u)
3. (lnu)′=
u
4. (sinu)′=cosu ∙(u)`
5. (cosu)′=-sinu ∙(u)`
6. (аu)′=аulnu ∙(u)`
(
u
)
7. (logau)′=
u ln a

5. Пример 1 Вычислить производную:

• (5sinx)′=5cosx
• (5sin(14х-3)′=5cos(14х-3)∙(14х-3) ′ =
=5cos(14х-3)∙(14·1-0) = 5cos(14х-3)∙14=
= 70 cos(14х-3)

6. Пример 2 Вычислить производную:

• (х7)'=7х6
• ((3х+15)7)'=7∙(3х+15)7-1 ∙(3х+15)'=
=7∙(3х+15)6∙(3·1+0)=
=7(3х+15)6∙3=21(3х+15)6

7. Задание 1: Найти производные следующих функций:

8. Самостоятельная работа

I вариант
1) ((12х-6)3)'
II вариант
1) ((5+13х)4)'
2) (sin ( 3 x 12) )'
2) (cos(6-7х )'
3) (ln(6+11х))'
3) (e5x+73)'