Похожие презентации:
Что называется производной?
1. Что называется производной?
Производной функции в даннойточке называется предел отношения
приращения функции в этой точке к
приращению аргумента, когда
приращение аргумента стремится к
нулю.
f ( x0 x) f ( x0 )
f ( x) lim
x 0
x
2. О происхождении терминов и обозначений производной и предела
• Термин «производная» - буквально перевод французского словаderivee.
• 1797г – Ж.Лагранж ввел современные обозначения
• И.Ньютон называл производную флюксией, а саму функцию –
флюентой.
• Г.Лейбниц говорил о дифференциальном отношении и
обозначал производную как
• Термин «предел» (lim – сокращение латинского слова limes
(межа, граница)) ввел И.Ньютон.
3. Правила дифференцирования
• 1).Производная суммы равна суммепроизводных, производная разности равна
разности производных:
(f(x) ± g(x))'= f '(x) ±g '(x)
• 2).Постоянный множитель можно вынести
за знак производной:
(Сf (x))'=Сf '(x)
• 3).Производная произведения:
(f(x)g(x)) '=f '(x)g(x) + f(x)g '(x)
4. Формулы дифференцирования
1. (хр)′=р·хр-11.1.(с)'=0, где с – число
1.2. (х)'=1
2. (ех)′=ех
1
3. (lnx)′= х , х>0
4. (sinx)′=cosx
5. (cosx)′=-sinx
6. (ах)′=ахlnx
7. (logax)′= 1
х ln a
5. Частного
Произведения(u v) u v u v
Частного
u
u v u v
( )
2
v
v
6. Вычислить производную функции
y3 x 2
5 x 8
3 x 2 5 x 8 3 x 2 5 x 8
y
2
5 x 8
3 5 x 8 3 x 2 5 15 x 24 15 x 10
2
2
5 x 8
5 x 8
3 x 2
5 x 8
34
.
2
5 x 8
u
u v u v
( )
2
v
v
7. Вычислить производную функции
f ( x) x (3x x )f ( x ) x 3 x x x 3 x x
2 x 3 x x x 3 x 3 x
2
2
2 1
3
3
3
2
3
1 1
2
3 1
2 x 3x 2 x x x 3 x x 3x
3
2
0
2
2
6 x 2 x 3x 3x 5 x 9 x .
2
4
2
4
4
2
(u v) u v u v
8. Задание 1:Найти производные:
f ( x ) (5 x 1)( 4 x 1)f ( x ) (5 x 2)( 4 x 1)
2
9. Задание 2:Вычислить производную:
2x 1y
2x 1
x 1
y 2
x 1
2
2x 3
y
5 4x




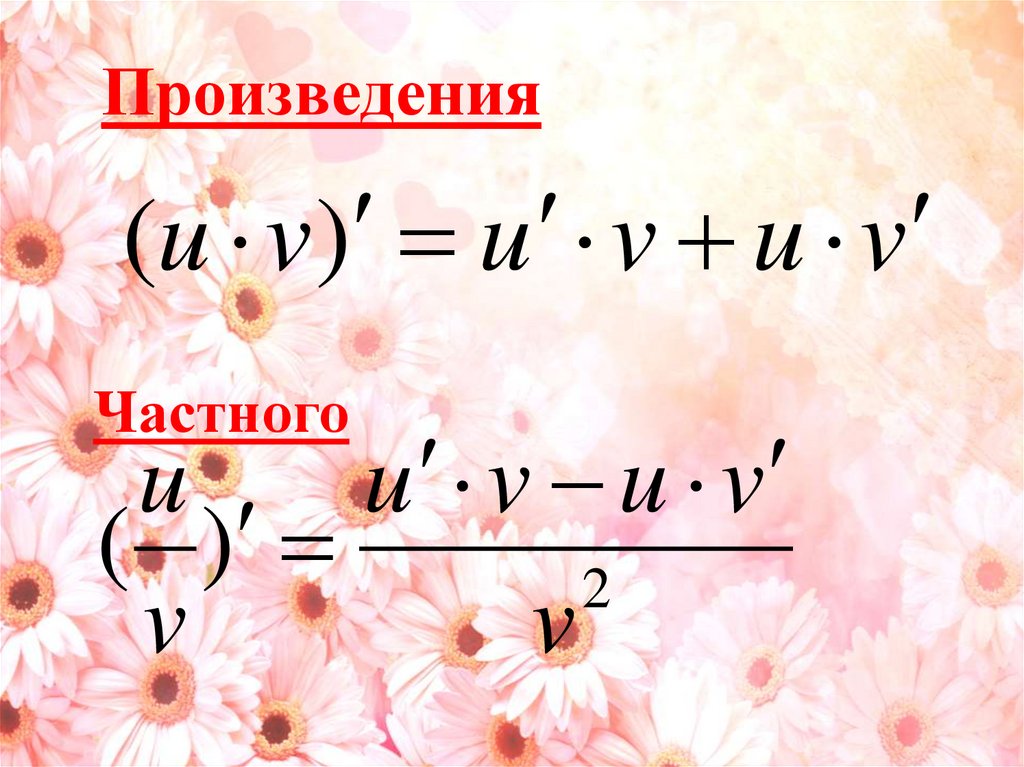




 Математика
Математика








