Advanced chapters of theoretical electroengineering

1.

Дополнительные главы ТОЭ.
ВШВЭ, ИЭ, СПбПУ, проф. А.Г. Калимов 2022
1

2.

Advanced chapters of
theoretical electroengineering.
HSHVPE, IE SPbPU, Prof. A.G. Kalimov 2022
2

3.

General information
Общая информация
Лектор – Калимов Александр Гелиевич,
профессор ВШВЭ ИЭ СПбПУ
Базовая литература:
1.K. Binns, P. Lawrenson. Analysis and computation of electric
and magnetic field problems
2. К. Бинс, П. Лауренсон. Анализ и расчет электрических
и магнитных полей.
Дополнительная литература:
3. Gunther Lehner. Electromagnetic Field Theory for Engineers and
Physicists.
3

4.

Analysis and computation of
electromagnetic fields.
4

5.

Lecture 1
Fundamental concepts of
electromagnetics.
Electrostatics.
(after: Gunther Lehner. Electromagnetic Field Theory for Engineers and Physicists)
5

6.

Vectors and scalar fields.
6

7.

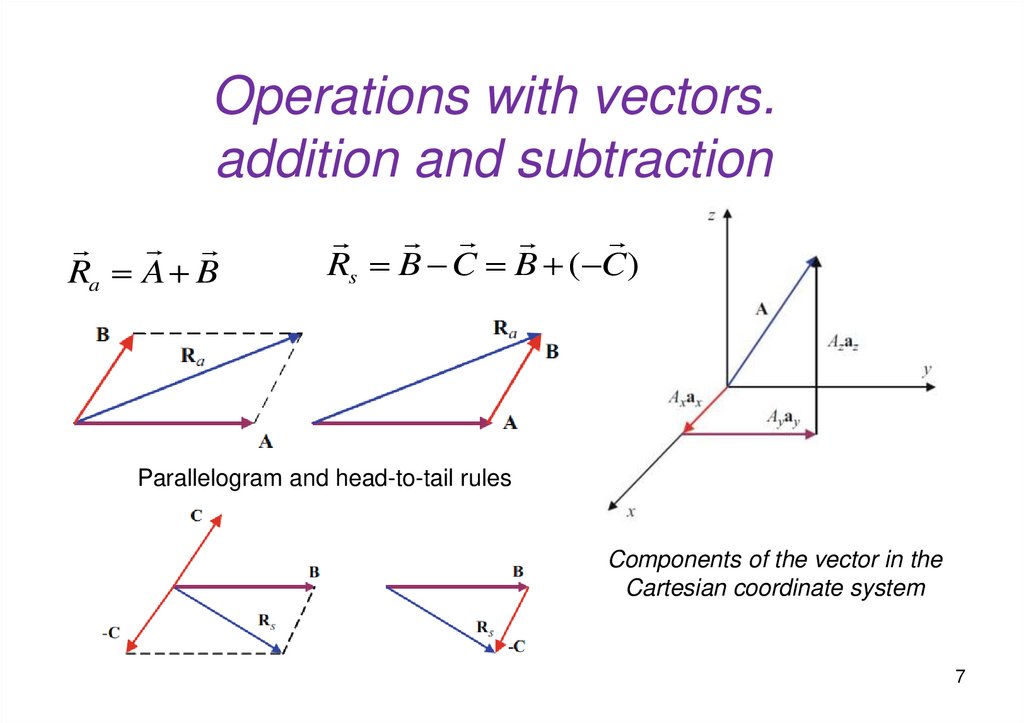
Operations with vectors.
addition and subtraction
Ra A B
Rs B C B ( C)
Parallelogram and head-to-tail rules
Components of the vector in the
Cartesian coordinate system
7

8.

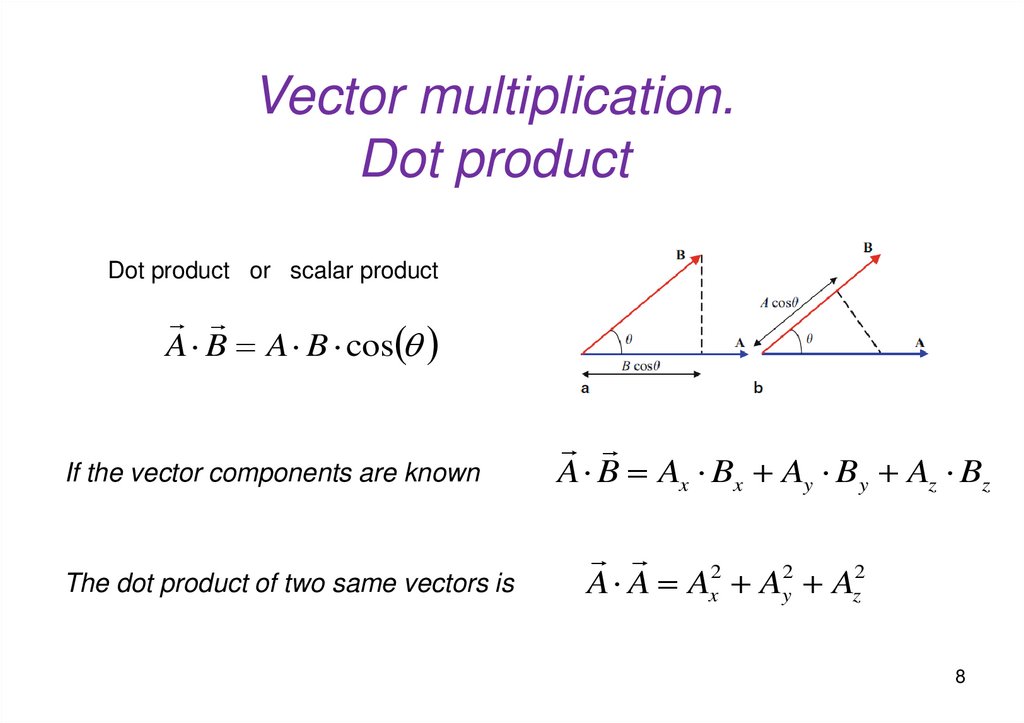
Vector multiplication.
Dot product
Dot product or scalar product
A B A B cos
If the vector components are known
The dot product of two same vectors is
A B Ax Bx Ay By Az Bz
A A Ax2 Ay2 Az2
8

9.

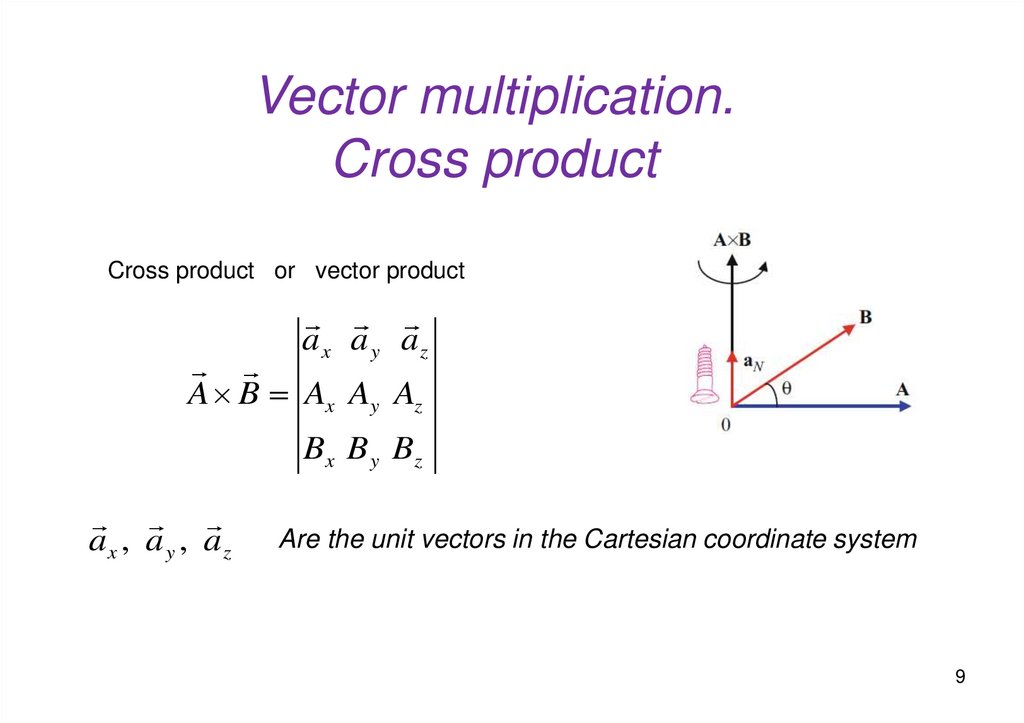
Vector multiplication.
Cross product
Cross product or vector product
ax a y az
A B Ax Ay Az
Bx B y Bz
ax , a y , az
Are the unit vectors in the Cartesian coordinate system
9

10.

Differential operations.
Gradient of a scalar field.
Object of operation is a scalar field
Result of operation is a vector field
Designation:
In the Cartesian
coordinate system:
grad (U ) U
U U U
grad (U )
ix
iy
iz
x
y
z
10

11.

Divergence of a vector field.
Object of operation is a vector field
Result of operation is a scalar
Designation:
div ( A) A
In the Cartesian coordinate system:
Ax Ay Az
div ( A)
x
y
z
11

12.

Circulation of a vector field.
curl ( A) A
In the Cartesian coordinate system:
ax a y az
A
x y z
Ax Ay Az
Ay Az Az Ax Ax Ay
ax
az
curl ( A)
a y
y
z
x
x
z
y
12

13.

Properties of the differential
operators.
Differential operations are linear:
grad ( U V ) grad (U ) grad (V )
div ( F G ) div ( F ) div (G )
curl ( F G ) curl ( F ) curl (G )
Important Vector Identities:
div curl ( F ) 0
curl grad (U ) 0
13

14.

Differential operator Nabla.
In the vector algebra an operator is often used
grad (U ) U
div ( F ) F
curl ( F ) F
In the Cartesian coordinate system:
ix
iy
iz
x
y
z
14

15.

Integral theorems.
V div( E )dV S E dS
V grad (U )dV S dS U
curl ( E )dV dS E
V
Different forms of
the Gauss theorem
S
curl ( A) dl A ds
l
S
Stoke’s theorem
15

16.

Electrostatic field.
16

17.

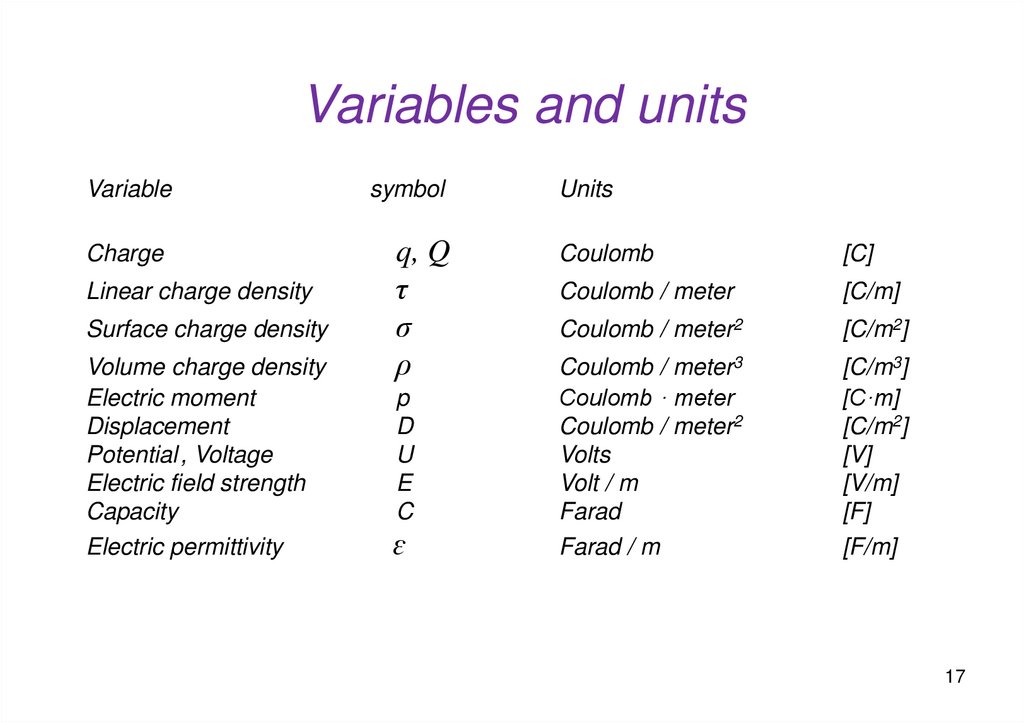
Variables and units
Variable
Charge
Linear charge density
Surface charge density
Volume charge density
Electric moment
Displacement
Potential , Voltage
Electric field strength
Capacity
Electric permittivity
symbol
q, Q
τ
σ
ρ
Units
Coulomb
[C]
Coulomb / meter
[C/m]
Coulomb / meter2
[C/m2]
p
D
U
E
C
Coulomb / meter3
Coulomb · meter
Coulomb / meter2
Volts
Volt / m
Farad
[C/m3]
[C·m]
[C/m2]
[V]
[V/m]
[F]
ɛ
Farad / m
[F/m]
17

18.

Coulomb’s Law
Coulomb’s law consists of two statements:
1. The force between two charges q1 and q2 is proportional to both q1 and q2
and also inversely proportional to the square of the distance between them
F~
q1 q2
r122
2. The axis of the force lies on the direct line between the charges; it is
repelling for like charges, and attractive for opposite charges.
q q
F12 1 2
4 0
(r1 r2 )
3
r1 r2
q q
F21 1 2
4 0
(r2 r1 )
3
r1 r2
F12 F21 0
18

19.

Electric Field Strength E and
Displacement Field D.
The electric field strength (intensity) is described by a vector quantity represented
by the symbol E. It is defined as the force in the field per unit charge
E
F
q
Field induced by the point charge
r2
unit - V/m
E r1
( r1 r2 )
4 0 r 1 r 2 3
q
defines a position of the point charge
Displacement vector
is also called
electric flux density
D E
unit - C/m2
19

20.

Gauss’ Law.
The electric flux:
D dS
S
Total electric flux passing any closed surface is
equal to the total charge enclosed by that surface
Integral form:
D ds q
Gauss law for
the field displacement
Differential form:
div D
q
E ds
Gauss law for
the field intensity
divE
0
20

21.

Electric Potential.
An electrostatic field may be described by different, but equivalent terms:
It is irrotational, curlE 0
The integral
l EB dl 0 vanishes
The integral
Edl solely depends
A
on the points A and B but not on the particular
path taken from A to B.
Definition of the potential: U ( B ) U ( A) E dl ;
B
E U
A
21

22.

Work in the Electric Field.
The field performs work on charges
Conversely, to move the charge against the field requires one to do work.
The force,
The work
F QE
B
A Fd l
A
A Q Edl
B
or
A
A Q U A U B
For infinitely remote point A:
A Q U B
The work against field forces: A Q U B
;
; this work increases the field energy
22

23.

Dielectric polarization.
Dielectric materials are polarized when an electric field is applied to them. As a
result, electric displacement becomes greater than under the free space condition:
D 0E P
The polarization is defined as the dipole moment per unit volume.
In isotropic and linear materials, the polarization is directly proportional to the
electric field and the proportionality constant does not depend on the field
P 0 E
is the susceptibility of dielectric material.
23

24.

Dielectric material characteristics.
In the linear dielectric material the field
intensity is proportional to the displacement
D E
r
0
0 1
D 0 E 0 E
is the dielectric permittivity (dielectric constant)
is the relative dielectric permittivity (dielectric constant)
In the case of extremely high electric field the electrons will accelerate and
collide with molecular lattice structure, which causes permanent damage to
the material. This phenomenon is known as dielectric breakdown.
24

25.

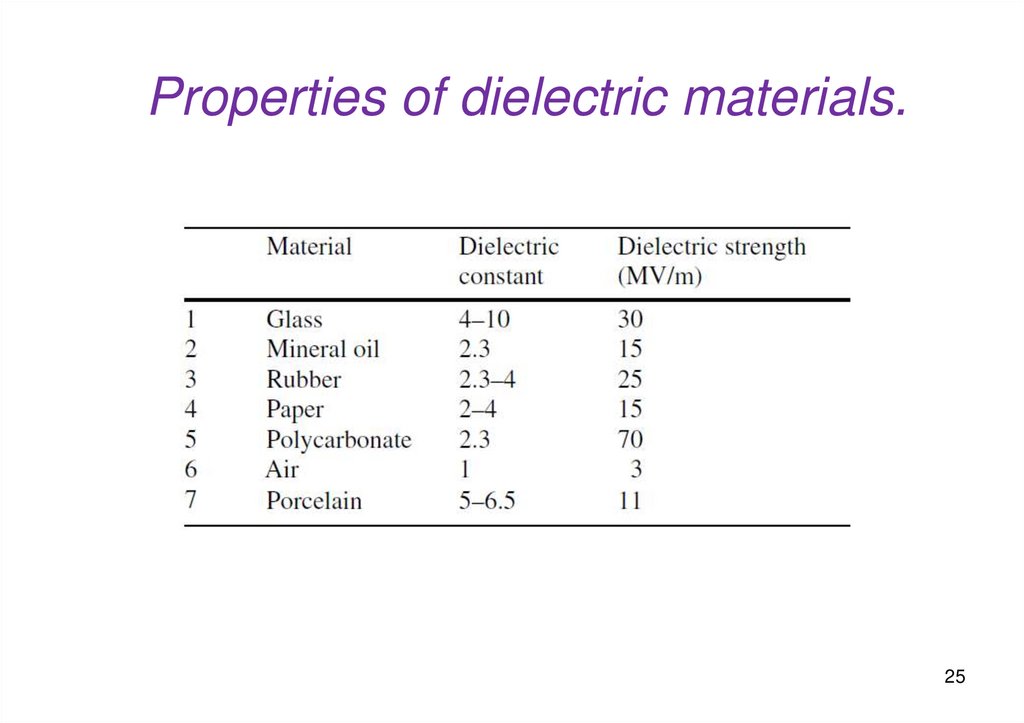
Properties of dielectric materials.
25

26.

Poisson’s and Laplace’ s equations.
E U
In the absence of free charges
D E
For the linear dielectric
const
2
In general case
For the linear dielectric
D 0
U 0
U 0
Laplace’s equation
U
U
Poisson’s equation
26