Похожие презентации:
Простейшие задачи в координатах
1.
2.
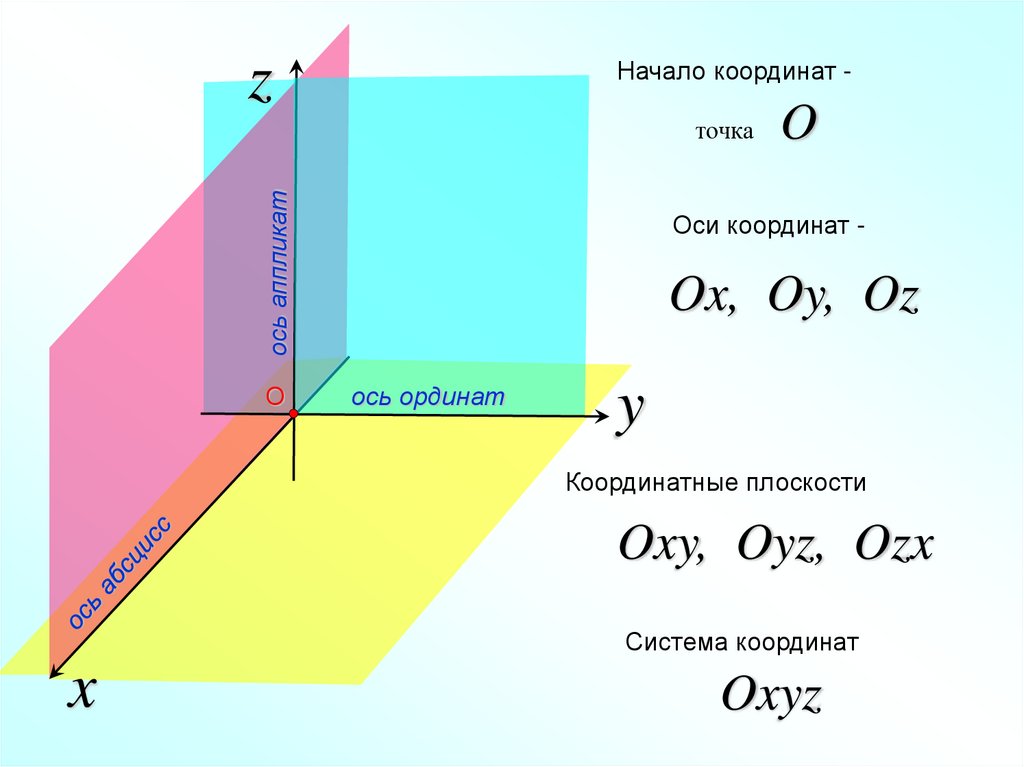
zНачало координат -
ось аппликат
точка
О
O
Оси координат -
Ox, Oy, Oz
ось ординат
y
Координатные плоскости
Oxy, Oyz, Ozx
Система координат
x
Oxyz
3.
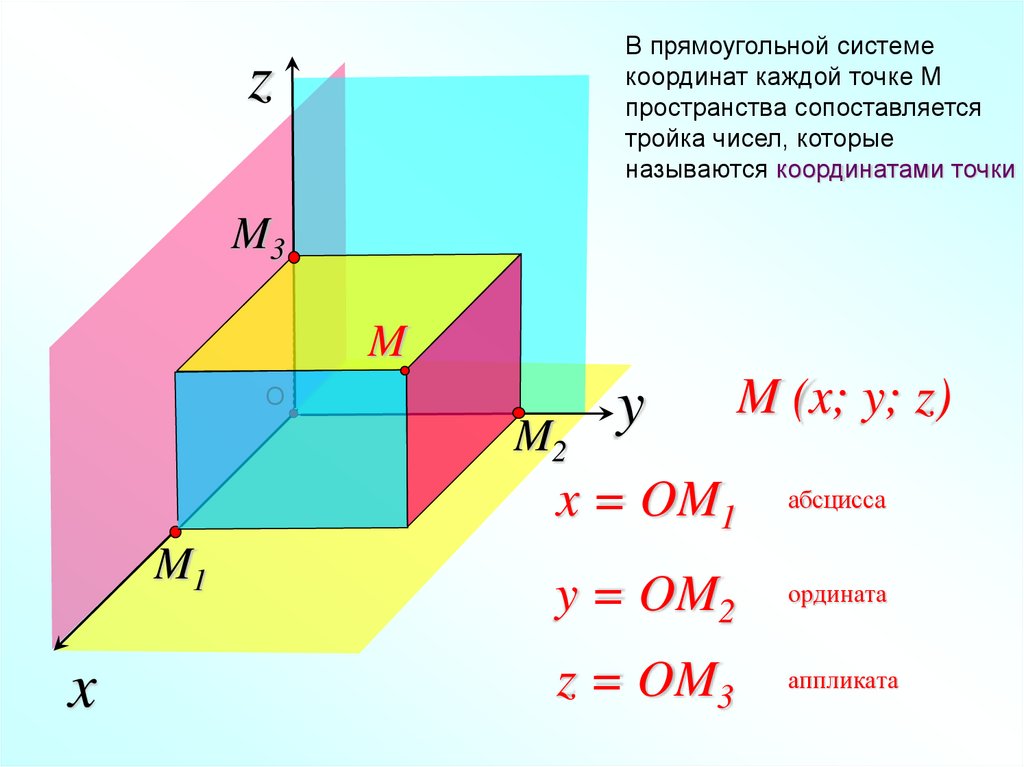
В прямоугольной системекоординат каждой точке М
пространства сопоставляется
тройка чисел, которые
называются координатами точки
z
M3
M
О
M2
M1
x
y
M (x; y; z)
x = OM1
абсцисса
y = OM2
ордината
z = OM3
аппликата
4. Выполнение задания с последующей проверкой.
Начертить прямоугольную трехмернуюсистему координат и отметить в ней
точки:
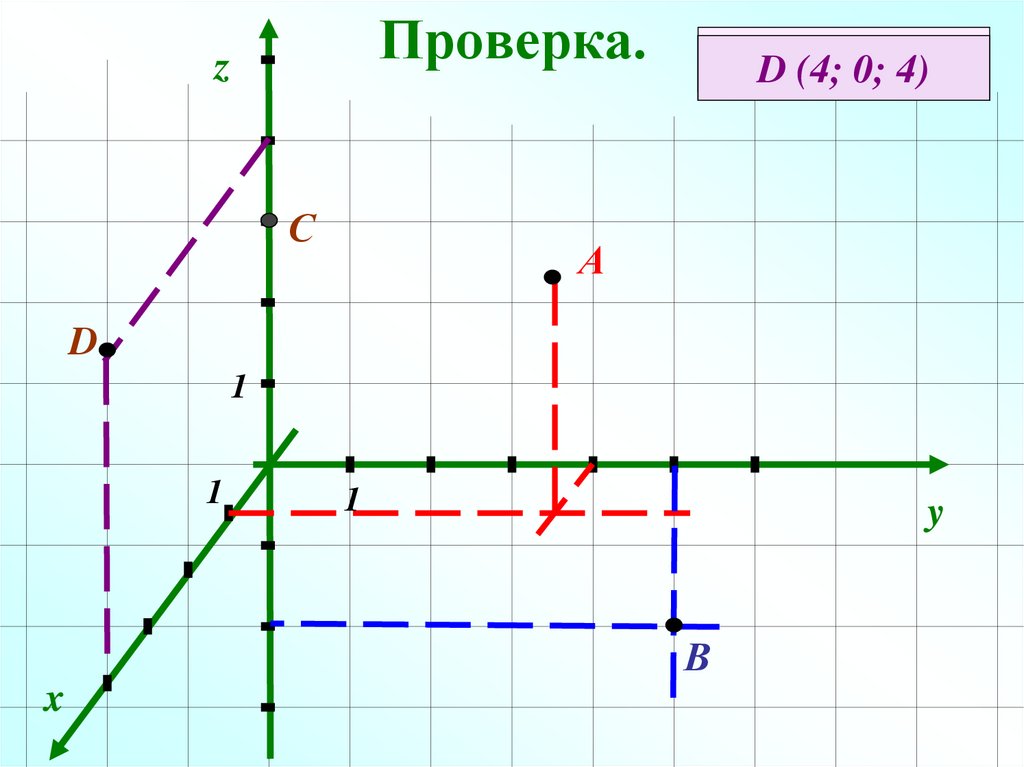
А (1; 4; 3); В (0; 5; -3); С (0; 0; 3) и D (4; 0; 4)
5. Проверка.
zС
А
(1;
4;
3)
В
D
С (0;
(0;
(4; 5;
0;
0; -3)
3)
4)
А
D
1
1
1
y
В
x
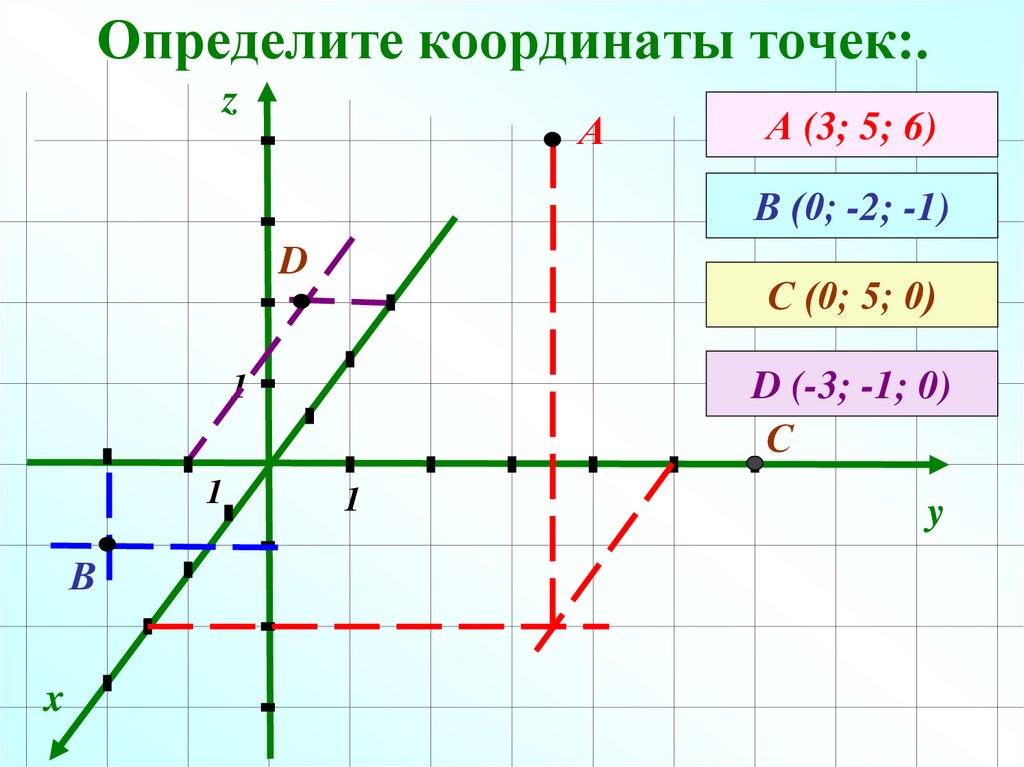
6. Определите координаты точек:.
zА
А (3; 5; 6)
В (0; -2; -1)
D
С (0; 5; 0)
D (-3; -1; 0)
С
1
1
В
x
1
y
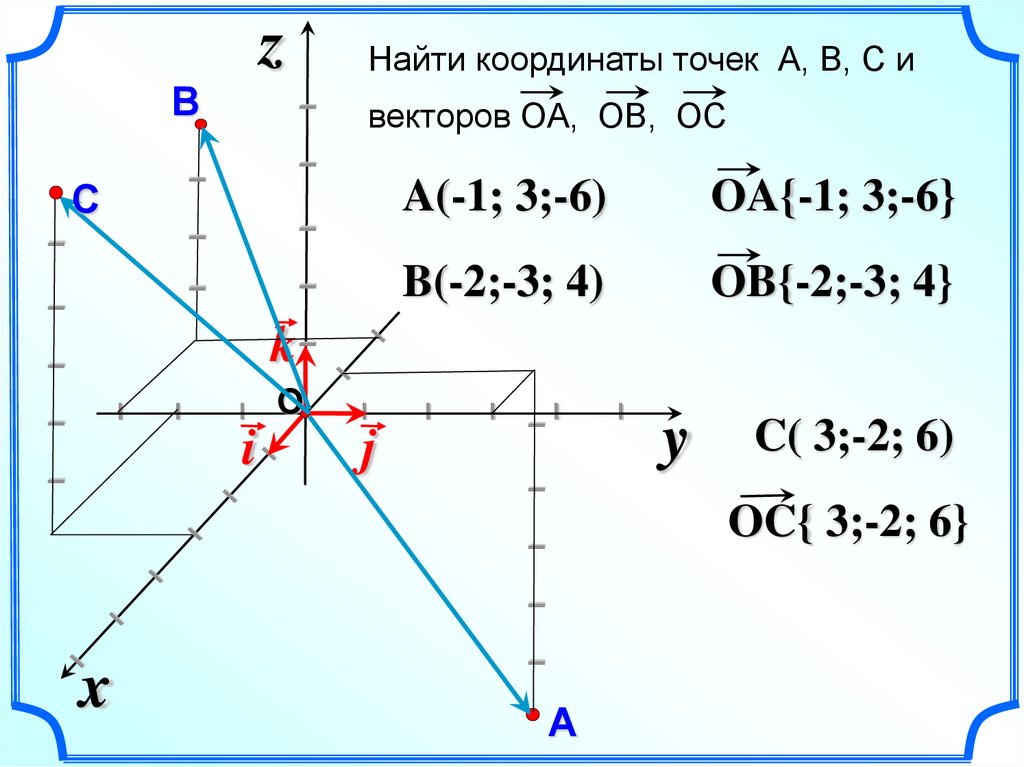
7.
zвекторов ОА, ОВ, ОС
I
I
I
В
Найти координаты точек А, В, С и
A(-1; 3;-6)
OA{-1; 3;-6}
B(-2;-3; 4)
OB{-2;-3; 4}
I
I
I
I
I
I
I
I
j
I
y
C( 3;-2; 6)
x
I
I
I
I
I
i
O
I
I
k
I
I
I
I
I
I
I
С
А
OC{ 3;-2; 6}
8.
ЗАДАЧА 1: Найти координаты векторов.a {2; 4; 3}; c {3; 2;-3}; a +c {
}
b{-2; 0; 4}; d{-2;-3;-1}; b+d{
}
c {2;-5; 4}; e {2;-3;-9}; c +e{
}
f(0; 5;-3}; d{-2;-3;7};
f - d{
}
b{-2; 0;-1}; d{-2;-3;-4}; b - d{
}
a {2; 4;0}; c {3; 2;-9}; a - c{
}
9.
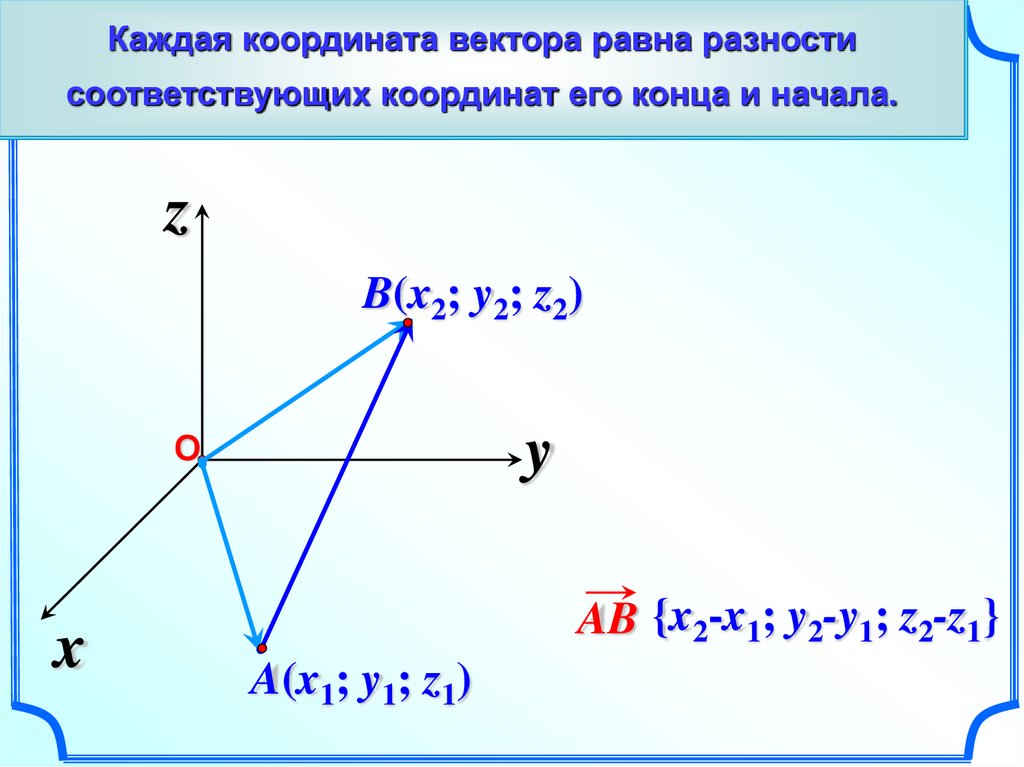
Каждая координата вектора равна разностисоответствующих координат его конца и начала.
z
B(x2; y2; z2)
y
О
x
AB {x2-x1; y2-y1; z2-z1}
A(x1; y1; z1)
10.
ПРИМЕР1: Вычислить координаты вектораA(3;5;7), B (5;4;-1), AB
A(3;5;7)
–
B(5;4;-1)
AB{2;-1;-8}
N(3;2;-3), O(0;0;0), ON
Радиус-вектор
P (2;-1;0), C (4;-4;2), PC
R(-4;0;-4), T (0;5;-1), TR
D(-3;-4;0), O(0;0;0), OD
Радиус-вектор
OD{-3;-4; 0}
ON{3; 2;-3}
P(2;-1;0)
–
C(4;-4;2)
PC{2;-3; 2}
R(-4;0;-4)
–
T(0; 5;-1)
TR{-4;-5;-3}
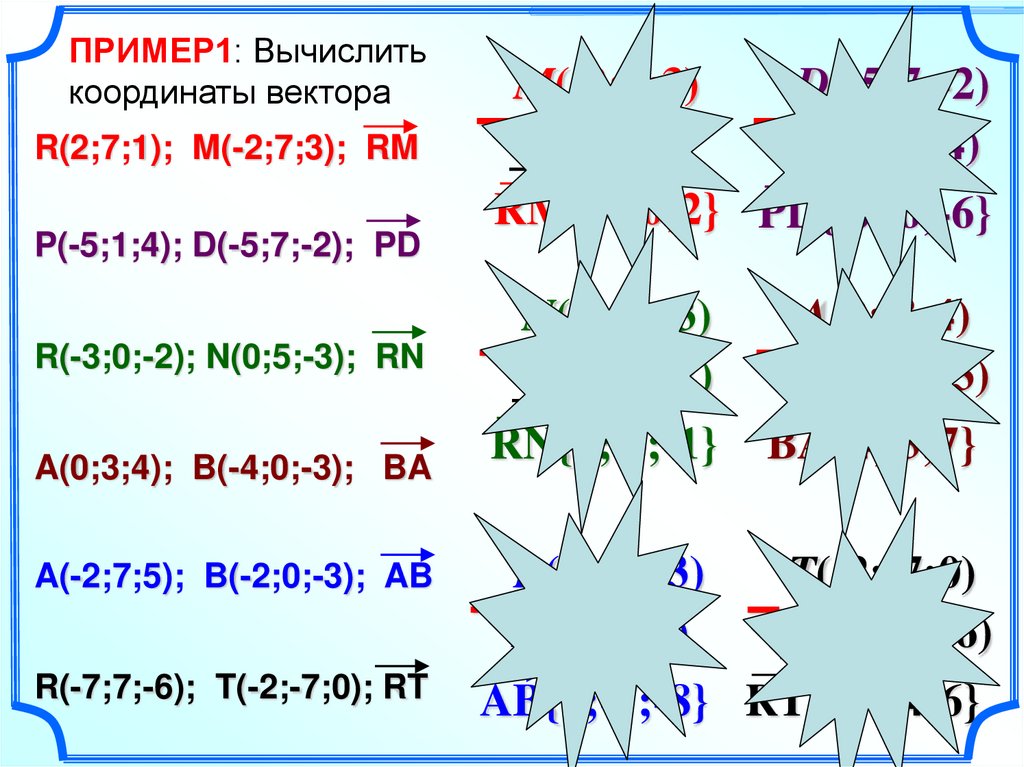
11.
ПРИМЕР1: Вычислитькоординаты вектора
R(2;7;1); M(-2;7;3); RM
P(-5;1;4); D(-5;7;-2); PD
R(-3;0;-2); N(0;5;-3); RN
A(0;3;4); B(-4;0;-3); BA
A(-2;7;5); B(-2;0;-3); AB
R(-7;7;-6); T(-2;-7;0); RT
M(-2;7;3)
D(-5;7;-2)
– R(2; 7;1) – P(-5; 1;4)
RM{-4;0;2} PD{ 0; 6;-6}
N(0; 5;-3)
– R(-3;0;-2)
RN{3; 5;-1}
A(0; 3;4)
– B(-4;0;-3)
BA{4; 3;7}
B(-2;0;-3)
T(-2;-7;0)
– A(-2;7;5) – R(-7; 7;-6)
AB{0;-7;-8} RT{5;-14;6}
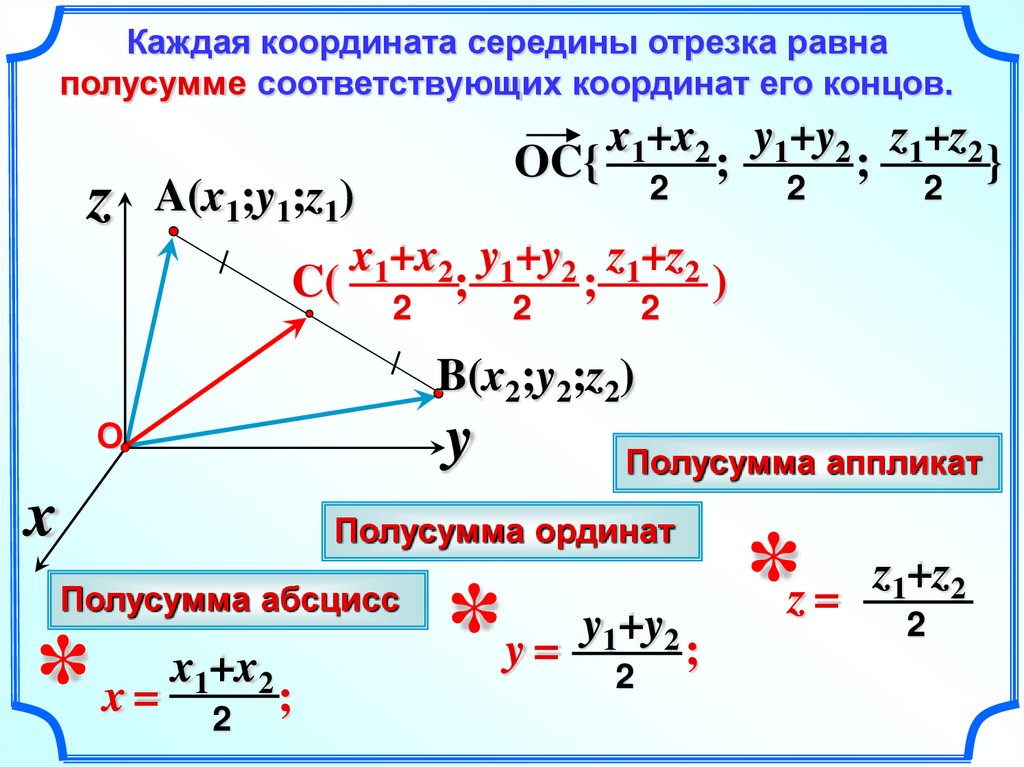
12.
Каждая координата середины отрезка равнаполусумме соответствующих координат его концов.
z
x1+x2 y1+y2 z1+z2
OC{
;
;
}
2
A(x1;y1;z1)
x1+x2 y1+y2 z1+z2
C(
;
;
)
2
2
2
2
2
B(x2;y2;z2)
y
О
x
Полусумма аппликат
Полусумма ординат
Полусумма абсцисс
* x=
x1+x2
2
;
*y =
y1+y2
2
;
*z =
z1+z2
2
13.
Пример 2:Найдите координаты середины отрезкаA(0; 3;-4), B(-2;2;0), середина – точка M(-1; 2,5; -2 )
Полусумма абсцисс
x=
x1+x2
y=
y1+y2
Полусумма ординат
Полусумма аппликат
z=
2
;
2
z1+z2
2
x=
0+(-2)
2
3 +2
= -1
;
y=
;
-4 +0
z = 2 = -2
2
= 2,5
14.
Пример 2: Найдите координатысередины отрезков
R(2;7;4); M(-2;7;2); C ( 2+(-2) ; 7 + 7 ; 4 + 2 )
2
2
2
-5+(-5) 1 + 7 3 +(-9)
(
;
;
)
P(-5;1;3); D(-5;7;-9); C
2
2
2
-3+0 0+5 -3+(-5)
; ;
);
R(-3;0;-3); N(0;5;-5); C (
2
2
2
A(0;-6;9); B(-4;2;-6);
0+(-4) -6+2
(
;
;
C
2
7+(-2)
A(7;7;0); B(-2;0;-4); C (
2
R(-7;4;0); T(-2;-7;0); C (
2
C(0; 7; 3)
C(-5; 4;-3)
C(-1,5;2,5;-4)
9+(-6) C(-2;-2;1,5)
);
2
7 + 0 0+(-4) C(2,5; 3,5;-2)
;
;
);
2
2
-7+(-2) 4+(-7) 0+0
;
; ); C(-4,5;-1,5;0)
2
2
2
15.
Вычисление длины вектора по его координатамz
a {x;y;z}
A3
A
zk a
О
xi
yj
A2
y
A1
x
2
2
a = x +y + z
2
16.
zРасстояние между двумя точками
d
M2(x2;y2;z2)
–
y
О
x
M1(x1;y1;z1)
M2(x2;y2;z2)
M1(x1;y1;z1)
M1M2 {x2–x1; y2–y1;z2–z1}
*
2
a = x +y + z
M1M2 = (x2–x1)2+(y2–y1)2+(z2–z1)2
*
2
d = (x2–x1)2+(y2–y1)2+(z2–z1)2
2
17.
Пример 3:Найдите длину вектора АВA(-35;-17;20)
B(-34; -5; 8)
– A(-35;-17;20)
AB{ 1; 12;-12}
2 способ
B(-34;-5;8)
a = x 2 + y 2 + z2
1 способ
1)
и
2)
AB = 12+122+(-12)2 =
= 289 = 17
AB = (x2–x1)2+(y2–y1)2+(z2–z1)2
AB = (-34+35)2+(–5+17)2+(8–20)2









 Математика
Математика








