Похожие презентации:
Случайные события
1. Случайные события
Ахмеджанова Т.Д.2. Случайное событие
Опыт, эксперимент, наблюдениеявления называется испытанием.
Результат, исход испытания
называется событием.
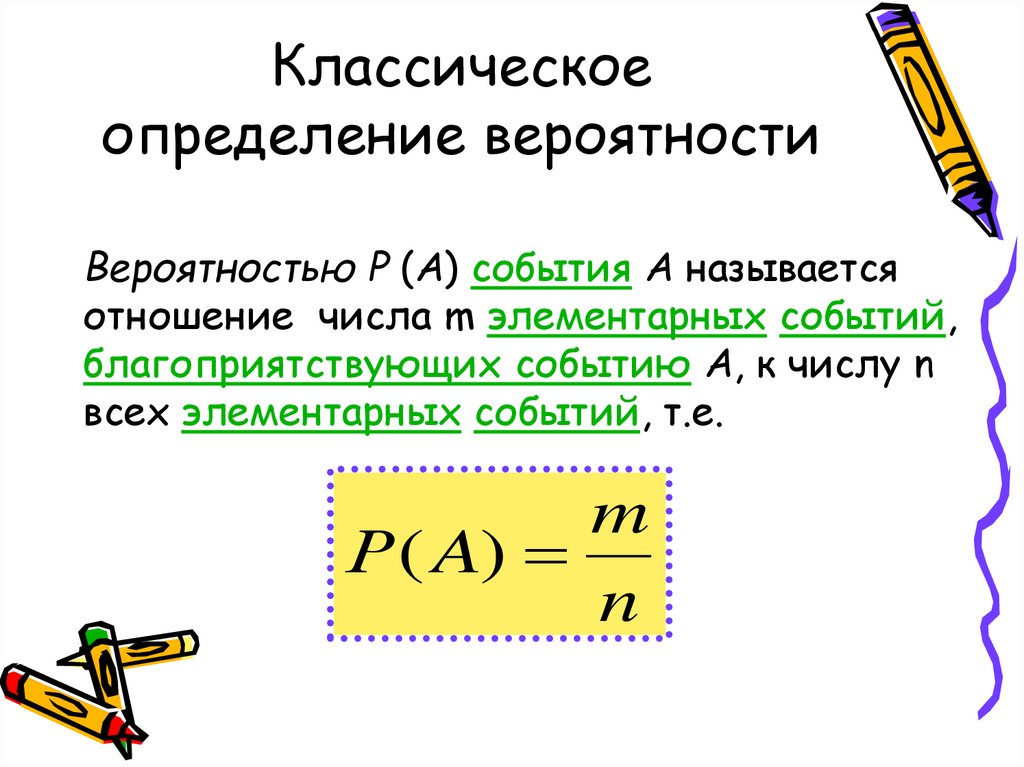
3. Классическое определение вероятности
Вероятностью Р (А) события А называетсяотношение числа m элементарных событий,
благоприятствующих событию А, к числу n
всех элементарных событий, т.е.
m
Р( A)
n
4. Событие А называется благоприятствующим событию В,
если наступление события Авлечет за собой наступление
события В.
5. элементарные события
События U1, U 2,…, Un, образующиеполную группу попарно
несовместимых и равновозможных
событий, называются
элементарными событиями.
6. совокупность событий образует полную группу событий для данного испытания,
если его результатом обязательностановится хотя бы одно из них.
7. Совместимые события
События называются совместимыми,если появление одного из них не
исключает появление другого в одном
и том же испытании.
В противном случае они называются
несовместимыми.
8. Равновозможные события
События Ui (i = 1, 2, 3,..., n)считаются равновозможными, если
условия испытания не создают
преимущества в появлении какоголибо события перед другими
возможными.
9. Задача 1
В урне 10 пронумерованных шаров сномерами от 1 до 10. Вынули один
шар. Какова вероятность того, что
номер вынутого шара не
превосходит 10?
10
9
8
7
6
5
4
3
2
1
10. Событие называется достоверным,
если в данном испытании оноявляется единственно возможным
его исходом.
11. Задача 2
В урне 15 шаров: 5 белых и 10черных. Какова вероятность вынуть
из урны синий шар?
12. Событие называется невозможным,
если в данном испытании онозаведомо не может произойти.
13. Задача 3
Из колоды в 36 карт вынимается однакарта. Какова вероятность появления
карты пиковой масти?
9 1
P( A)
36 4
14. Задача 4
Бросаются одновременно две монеты.Какова вероятность выпадения цифры
на обеих монетах?
15. Решение
Составим схему возможных случаев.1 случай
2 случай
3 случай
4 случай
Первая
монета
герб
герб
цифра
цифра
Вторая
монета
герб
цифра
герб
цифра
Всего случаев 4. Благоприятствующих случаев 1.
Р = 1/4.
16. Задача 5
В урне 10 шаров: 6 белых и 4черных. Вынули два шара. Какова
вероятность, что оба шара белые?
17. Решение
10 9n C
45
2
2
10
m C 15
2
6
m 15 1
p
n 45 3
4
6
18. Задача 6
В цехе работают 6 мужчин и 4женщины. По табельным номерам
наудачу отобраны 7 человек. Найти
вероятность того, что среди
отобранных лиц три женщины.
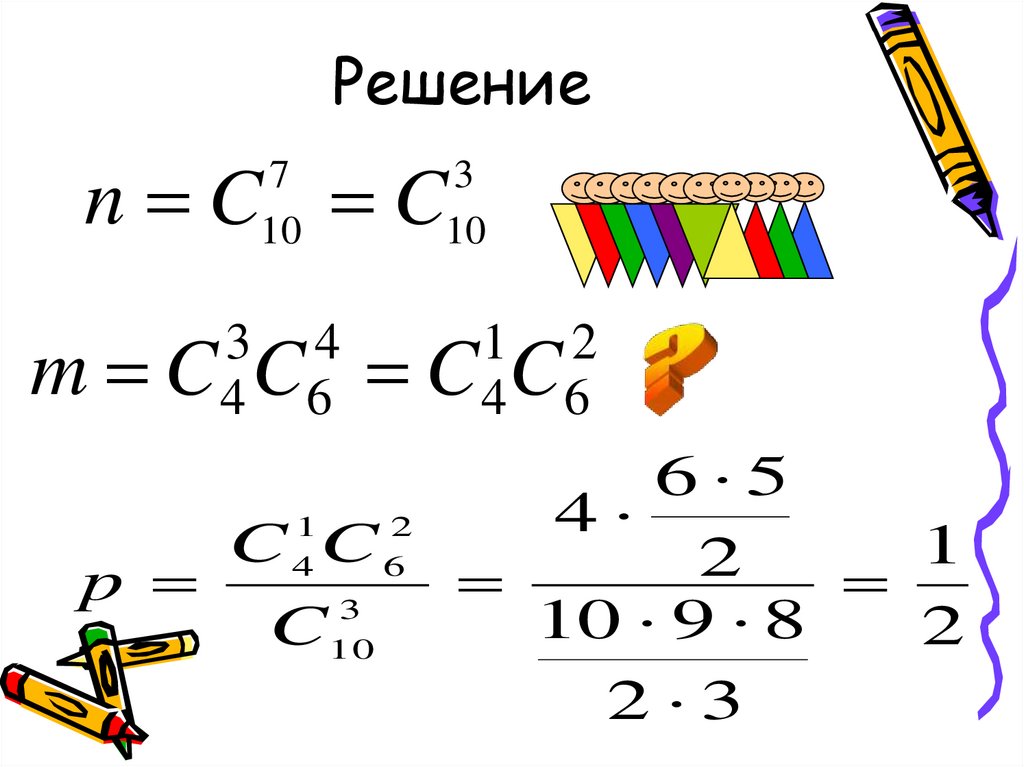
19. Решение
n C C7
10
m
3 4
C 4 C6
1
4
3
10
1 2
C 4 C6
C C
p
3
C10
2
6
6 5
4
1
2
10 9 8
2
2 3
20. Свойства сочетаний
n0
Сn Сn 1
1
n 1
Сn Сn
n
m
n m
Сn Сn
21. Задача 7
Пять книг расставляются на полку.Найти вероятность того, что две
определенные книги окажутся рядом.
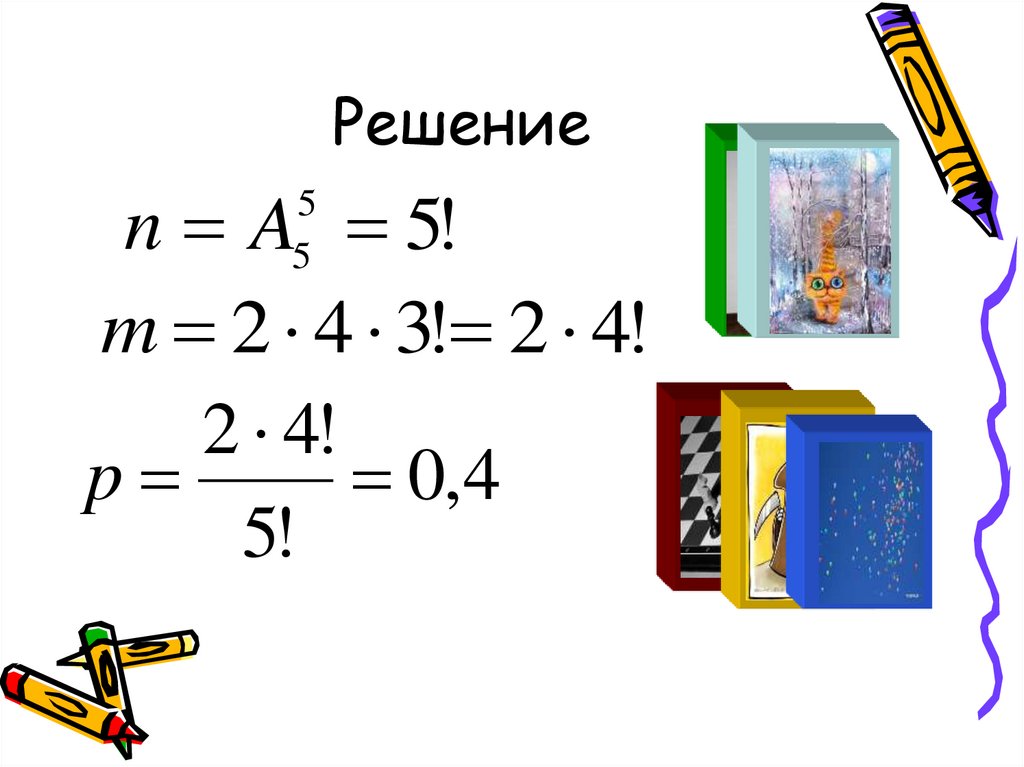
22. Решение
n A 5!m 2 4 3! 2 4!
2 4!
p
0,4
5!
5
5
23. Задача 8
В урне 10 белых, 15 черных, 20синих и 25 красных шаров. Вынули
один шар. Найти вероятность того,
что вынутый шар а) синий или
черный; б) белый, черный или
синий.
10
15
20
25
24. Решение
10P( Б )
70
20 15 1
P(C Ч ) P(C ) P(Ч )
70 70 2
15
P(Ч )
70
10 15 20 9
P( Б Ч C ) P( Б ) P(Ч ) P(C )
70 70 70 14
20
P (C )
70
25
P( K )
70
25 9
P( Б Ч C ) 1 P( K ) 1
70 14
10
15
20
25
25. Задача 9
На стеллаже в библиотеке стоит 15учебников, причем 5 из них в
переплете. Библиотекарь берет три
учебника. Найти вероятность того, что
хотя бы один из взятых учебников
окажется в переплете.
26. Решение
I способ.А – хотя бы один учебник в переплете:
В – один в переплете, два – без переплета;
С – два в переплете, один без переплета;
D – все три в переплете.
А = В + С + D.
P( A) P( B) P(C ) P( D)
1 2
C5C10
3
C15
2 1
C5 C10
3
C15
3
C5
3
C15
45 20 2 67
91
91
27. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
P( A B) P( A) P( B)28. Решение
II способ.А – хотя бы один учебник в переплете;
A - ни один из взятых учебников не имеет
переплета.
3
10
C
24 67
P( A) 1 P( A) 1 3 1
C15
91 91
29. Сумма вероятностей противоположных событий равна единице:
P( A) P( A ) 130. Теорема умножения вероятностей
• Вероятность произведения двухзависимых событий А и В равна
произведению вероятности одного из
них и условной вероятности другого,
найденной в предположении, что первое
событие уже наступило:
Р (АВ)=Р(А)Р(В А).
31. Вероятность произведения двух независимых событий
равна произведению вероятностейэтих событий:
Р (АВ)=Р(А)Р(В).
32. Теорема сложения вероятностей совместных событий.
• Вероятность суммы двухсовместных событий А и В равна
сумме вероятностей этих событий
минус вероятность их
произведения:
Р (А+В) = Р (А)+Р (В) - Р (АВ).
33. Задача 10
В первом ящике 2 белых и 7 черныхшаров, во втором 8 белых и 4 черных
шара. Из каждого ящика вынули по
шару. Найти вероятность того, что один
из вынутых шаров белый, а другой –
черный.
2
7
8
4
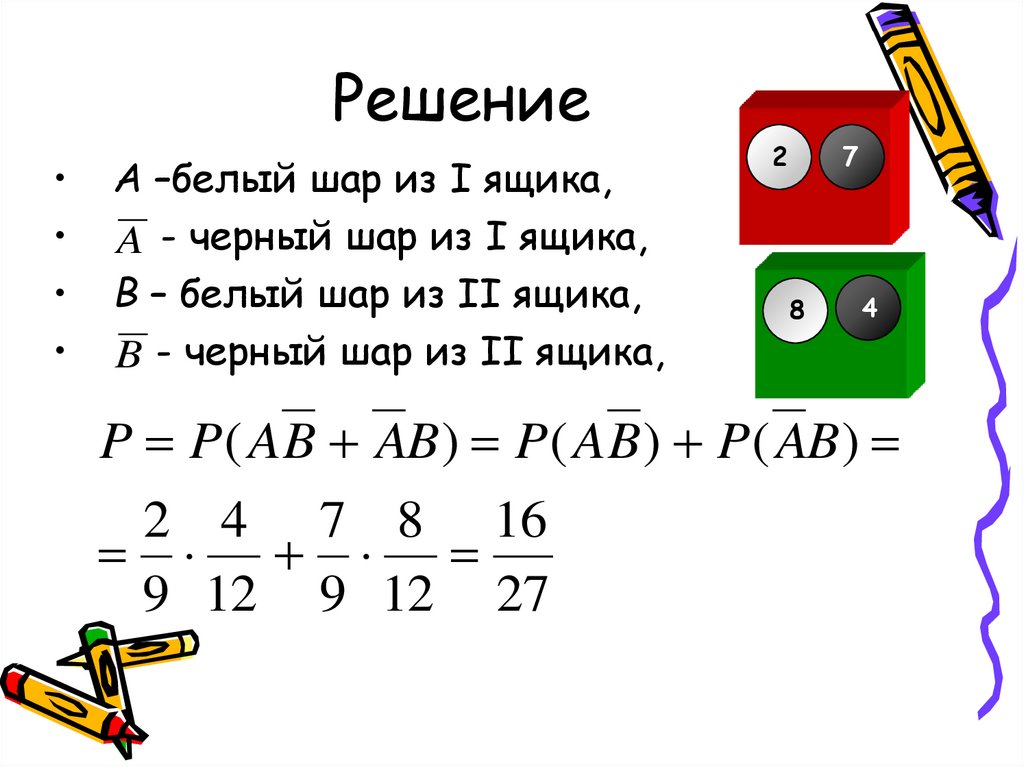
34. Решение
А –белый шар из I ящика,
A - черный шар из I ящика,
В – белый шар из II ящика,
B - черный шар из II ящика,
2
7
8
4
P P ( A B AB ) P ( A B ) P ( AB )
2 4 7 8 16
9 12 9 12 27
35. Задача 11
• Вероятность попадания в цель упервого стрелка 0,8, у второго – 0,9.
Стрелки делают по выстрелу.
Найти вероятность: а) двойного
попадания; б) хотя бы одного
попадания; г) одного попадания.
36. Задача 12
• Студент разыскивает нужную емуформулу в трех справочниках.
Вероятности того, что формула
содержится в первом, втором и третьем
справочниках равны 0,6; 0,7 и 0,8. Найти
вероятности того, что формула
содержится 1) только в одном
справочнике; 2) только в двух
справочниках; 3) во всех трех
справочниках.
37. Задача 13
• Из 10 деталей 7 – стандартные.Наудачу берут 6 деталей. Найти
вероятность того, что среди них: а)
не более одной нестандартной; б)
не более двух нестандартных.
38. Задача 14
На полке 10 пар разных перчаток.Наудачу выбираются 4 перчатки.
Найдите вероятность того, что среди
них окажется хотя бы одна пара.



































 Физика
Физика








