Численное моделирование разложения газогидрата в пласте при отборе газа

1. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАЗЛОЖЕНИЯ ГАЗОГИДРАТА В ПЛАСТЕ ПРИ ОТБОРЕ ГАЗА

Выпускная квалификационная
работа
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
РАЗЛОЖЕНИЯ ГАЗОГИДРАТА В
ПЛАСТЕ ПРИ ОТБОРЕ ГАЗА
Выполнил:
студент 4 курса группы ПМИ-41
Галиаскаров А.Р.
Научный руководитель:
к.ф-м.н., доцент
Хасанов М.К.

2. Цель работы:

теоретическое изучение особенностей
разложения газовых гидратов при
тепловом и депрессионном воздействии
на пористую среду, частично
насыщенную гидратом.

3. Задачи работы:

изучить теоретические аспекты образования и
существования газогидратов;
построить аналитические решения плоскоодномерной
задачи разложения газогидрата при депрессионном
воздействии, позволяющие оценить давления и
температуры на границе фазовых переходов и в зоне
разложения;
проанализировать результаты моделирования

4. Кратко о газогидратах

Газовые гидраты – кристаллические соединения,
образующиеся при определенных термобарических
условиях из воды и газа.
В общем виде состав газовых гидратов описывается
формулой M*nH2O, где М – молекула газагидратообразователя, n – число, показывающее
количество молекул воды, приходящихся на одну
молекулу газа

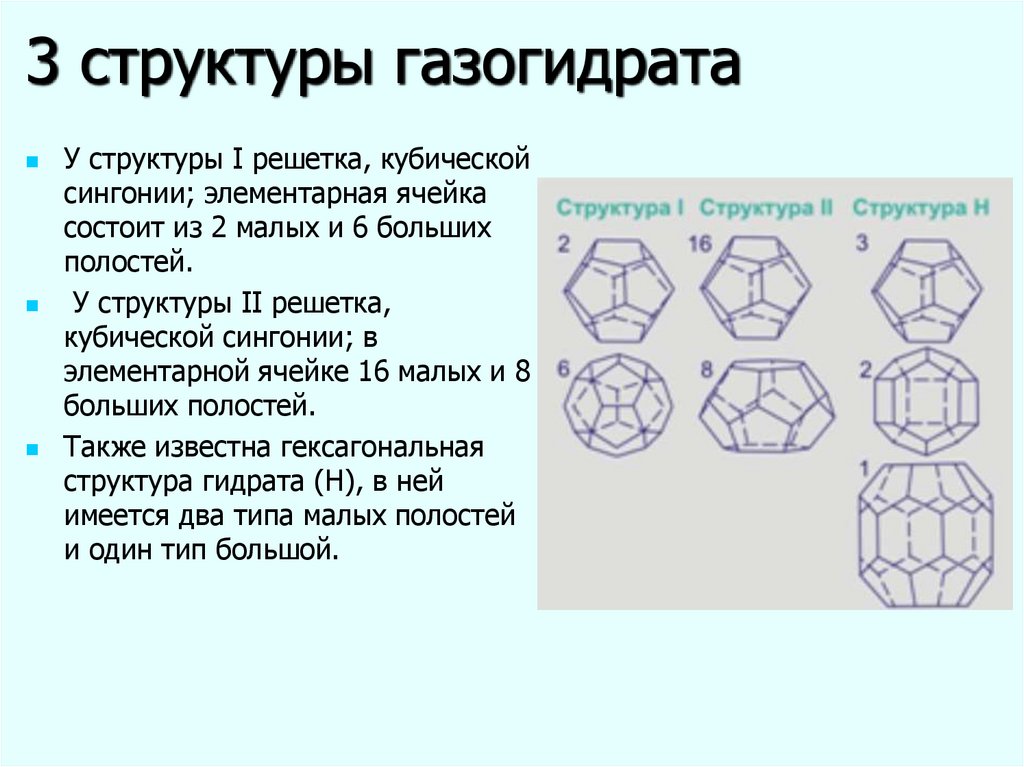
5. 3 структуры газогидрата

У структуры I решетка, кубической
сингонии; элементарная ячейка
состоит из 2 малых и 6 больших
полостей.
У структуры II решетка,
кубической сингонии; в
элементарной ячейке 16 малых и 8
больших полостей.
Также известна гексагональная
структура гидрата (H), в ней
имеется два типа малых полостей
и один тип большой.

6. Использование газогидрата

Газогидрат - самый богатый на нашей планете
источник углеводородного газа
Также использование газогидрата, может повлечь
ряд экологических проблем

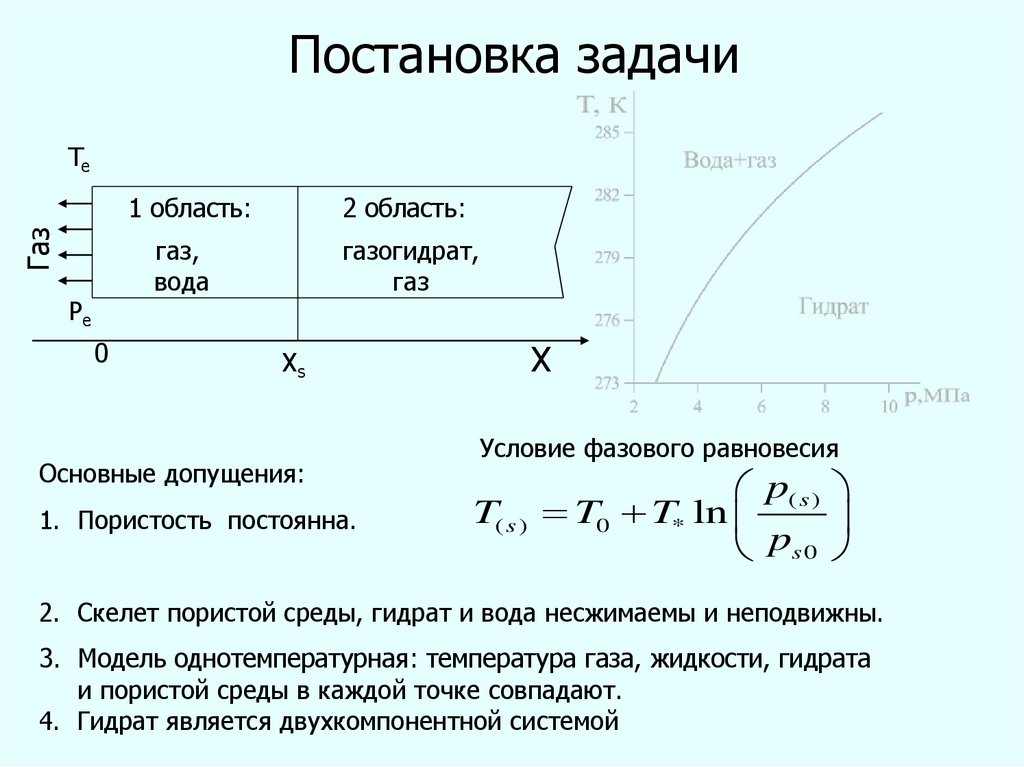
7. Постановка задачи

Te
Газ
1 область:
2 область:
газ,
вода
Pe
0
газогидрат,
газ
X
Xs
Основные допущения:
1. Пористость постоянна.
Условие фазового равновесия
T( s )
p( s )
T0 T* ln
p
s0
2. Скелет пористой среды, гидрат и вода несжимаемы и неподвижны.
3. Модель однотемпературная: температура газа, жидкости, гидрата
и пористой среды в каждой точке совпадают.
4. Гидрат является двухкомпонентной системой

8. Основные уравнения

1. Уравнение сохранения массы газа: mS g ( i )
2. Закон Дарси:
mS g (i ) g (i )
g (i )
t
m S g (i ) g (i ) g (i ) 0
x
k(i ) p(i )
g x
3. Газ считаем калорически совершенным:
p i g (i ) RgT i
4. Уравнение притока тепла, принебрегая
баротермическим эффектом:
c
λ – коэффициент теплопроводности
T(i )
t
g (i )cg m S g (i ) g (i )
T(i )
x
T(i )
x x
c (1 m) s c s mS g g c g mSl l cl mS h h c h
(1 m) s mS g g mSl l mS h h

9. Начальные и граничные условия

Уравнения баланса массы и тепла на границе фазового перехода:
( 2)
m (1 g ) xs mSl (1) xs
0
h
0
l
T( 2)
x
(1)
T(1)
x
m l xs
0
h
0
0
0
m (1 ) g ( s ) ( g ( 2 ) xs ) h g xs mS g (1) g ( s ) ( g (1) xs )
p
T( s ) T0 T ln ( s )
ps 0
Условие фазового равновесия:
Давление и температура в начальный момент времени:
p(2) p0 ,
T(2) T0 , (t 0, x 0)
Непрерывность давления и температуры
на границе фазового перехода:
Условия на границе пласта:
p(1) p(2) p( s ) , T(1) T(2) T( s ) ( x x( s ) )
T(1) Te , p(1) pe , (t 0, x 0)

10. Аналитическое решение

Автомодельная переменная:
x
Распределение давления:
2
0 exp 4 (1) d
, (0 ),
p(21) p(2e ) ( p(2s ) p(2e ) ) ( s )
(s)
2
0 exp 4 (1) d
(T )
(T )t
c
2
exp 4 (2) d
(s)
, ( s )
2
exp 4 (2) d
(s)
p(22) p(2s ) p02 p(2s )
Распределение температуры:
2 2 2
p 2 d
T0 Ts exp
4
2
s
Ts
2 2 2
exp 4 2 p 2 d
s
(1)
Ts Te exp p 2 1 d
2
4
0
T(1) Te
s
2 (1) 2
0 exp 4 2 p 1 d
2
T(2)

11.

Перейдем к автомодельной переменной:
.
d
1
x
d
,
(
T
)
t t d
2 t t d
d
1
d
x x d
(T ) t d
Тогда координата границы и скорость ее движения:.
xs s t ,
(T )
xs
s (T )
2
(T ) t
На основе уравнения неразрывности, используя закон Дарси (2) с учетом,
что газ является калорически совершенным (3), получим уравнение пьезопроводности:
,
p( i ) k( i ) p( i )
t
x m(i ) g x
p(i )
Уравнение притока тепла, используя закон Дарси, можно преобразовать к следующему виду:
2
T(i ) g i cg k(i ) p(i ) T(i )
(T )
2
t
x
c g x x
T(i )

12.

где c
(T )
– коэффициент температуропроводности
Из уравнения Баланса массы, учитывая равенство
S g (1) 1 S l (1)
S g (1) S l (1) 1 получим:
h0 (1 g )
1
l0
Тогда учитывая последнее уравнение и уравнение закона сохранения массы, применив закон
Дарси можно записать:
k ( 2) p( 2)
g ( 2) x
h0 g h0 (1 g )
mv 0
1 x s
0
x
l
g (s)
k (1) p(1)
g (1)
Запишем уравнение пьезопроводности в автомодельных переменных:
dp( i )
2 d k( i )
(T )
p(i )
d d g m(i )
d
dp(i )
Применяя метод линеаризации Лейбензона, уравнение запишем в виде:
2
d dp(i )
2 ( i )
d
d d
dp(2i )

13.

где
,
( i )
i
( p)
i
(T )
Введем обозначение
p i
dp(2i )
d
( p)
k( i )
g m(i )
p0
. Тогда последнее уравнение запишется в виде:
dp i
d
Это уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:
.
,
Отсюда:
dp i
p i
1
2 i
d
2
p i
Ci ( p ) exp
d
4 i
dp(2i )
.
p D1( p ) C1( p )
2
(1)
0
2
d
exp
4
(1)
D2( p ) C2( p )
2
( 2)
p
( s )
.
2
d
exp
4
2
p 0
2 (i ) i

14.

Коэффициенты
Ci ( p )
и
Di ( p )
найдем из начальных и граничных условий:
0, p(1) p(e) D1( p ) p(2e)
( s ) , p( 2 ) p( s ) , D2 ( p ) p(2s ) ,
, p( 2) p0 , C2 ( p )
p02 p(2s )
2
exp 4 2 d
(s)
( s ) , p(1) p( s ) , C1( p )
,
p(2s ) pe2
(s)
0
2
d
exp
4
(1)
Тогда для распределения давления в первой и второй зонах получим уравнения:
2
0 exp 4 (1) d
p(21) p(2e ) ( p(2s ) p(2e ) ) ( s )
, (0 ( s ) )
2
0 exp 4 (1) d
2
exp 4 ( 2) d
(s)
. ( s )
2
exp 4 ( 2) d
(s)
p(22 ) p(2s ) p02 p(2s )

15.

Запишем уравнение баланса массы газа на границе между зонами в автомодельных переменных:
g (1 g )
k ( 2 ) p 2 ( 2) k (1) p 2 (1)
m h h
1 x( s ) , x x( s )
g
g
g ( s )
l
С учетом полученного решения получим:
(2s )
( p p ) exp
4 ( 2 )
2
exp 4 ( 2) d
(s)
2
0
k ( 2)
2
(s)
k
(2s )
( p p ) exp
4 ( 2)
( s )
2
0 exp 4 ( 2) d
2
(s)
(1)
2
(e)
m h g h (1 g ) 1 x
(s) g
l
g ( s )
Отсюда после преобразований получаем уравнение для нахождения
p (2s )
Где,
,
ps
h g h (1 g )
m
1 x ( s ) g
l
k ( 2 ) A p 02 k (1) B p e2
g ( s )
k ( 2 ) A k (1) B
k ( 2 ) A k (1) B
(2s )
exp
4
(2)
A ( s )
(2s )
0 exp 4 (1) d
(2s )
exp
4
(1)
B
(2s )
exp 4 (2) d
(s)

16.

Запишем уравнение притока тепла в автомодельных переменных:
2
где,
(i )
g 0 c g k( i )
p0 g
dp i dT i
1 dT(i ) d dT(i ) 1
(i )
2 d
d d 2
d d
Введем обозначение
.
T (i )
dT(i )
d
2
dp
dT (i )
(i ) i
T (i ) 0
2 2 d
d
Это уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:
dT (i )
,
T (i )
T
(i )
i
1
2
d
dp
(
i)
2
2
2 (i ) 2
Ci (T ) exp
p i
d
2
4
.
dT(i )

17.

Отсюда
.
2 (1) 2
T(1) D1(T ) C1(T ) exp
p 1 d
4
2
0
Коэффициенты
Ci ( p ) и Di ( p )
2 (2) 2
D2(T ) C2(T ) exp
p 2 d
4
2
( s )
T(2)
найдем из начальных и граничных условий:
( s ) , T(2) T( s ) , D2(T ) T( s )
, T(2) T(0) , C2(T )
и
,
,
T0 T( s )
2 (2) 2
exp 4 2 p(2) d
(s)
0, T(1) T(e) , D1(T ) T(e)
( s ) T(1) T( s ) , C1 T
T( s ) T( e )
2 (1) 2
0 exp 4 2 p(i ) d
.
Тогда для распределения температуры в первой и второй зонах получим уравнения:
2 (1) 2
Ts Te exp p 1 d
2
4
0
T(1) Te
s
2 (1) 2
0 exp 4 2 p 1 d
2 2 2
p 2 d
T0 Ts exp
4
2
s
Ts
2
2 2
exp 4 2 p 2 d
s
T(2)

18.

Запишем уравнение баланса тепла на границе между зонами в автомодельных координатах:
m h0l
s
d
d
2 c
dT(1)
dT( 2)
Подставив в это уравнение полученные решения, получим:
1 2
T0 Ts exp 2 ps 2
ps
0
2
2
2
m h l exp s
4 s
2 c
2 2 2
2 1 2
0 exp 4 2 p 1 d exp 4 2 p 2 d
Ts Te exp
S
S
Заменив в этом уравнении
p s и Ts их значениями, получим
уравнение для нахождения
s ,
которое решается численно.
Таким образом, для построения профилей давлений и температур имеем:
2
exp
0 4 (1) d
,
p(21) pe2 ( ps2 pe2 )
s
2
exp
0 4 (1) d
2
exp
4 ( 2) d
,
p(22 ) ps2 p02 ps2 s
2
exp 4 ( 2) d
s
0 s
2 1 2
Ts Te exp p 1 d
2
4
,
0
T(1) Te
s
2
1 2
0 exp 4 2 p 1 d
s
T( 2 ) Ts
2
p 2 2 d
2
4
s
.
2
2 2
exp 4 2 p 2 d
s
T0 Ts exp
2
0 s
s

19. Нахождение граничных параметров

Условие баланса тепла:
1 2
T0 Ts exp 2 ps 2
ps
0
2
2
2
m h l exp s
4 s
2 c
2 2 2
2 1 2
exp
p
2 d
exp
p
1 d
4 2
0 4 2
Ts Te exp
S
S
h g h (1 g )
k ( 2) p 2 ( 2) k (1) p 2 (1)
Условие баланса массы:
m
1 x( s ) , x x( s )
g
g
l
g ( s )
Условие фазового равновесия:
(T )
c
p( s )
T( s ) T0 T ln
p
s0
g 0 c g k( i )
(i )
p0 g
Результаты расчётов

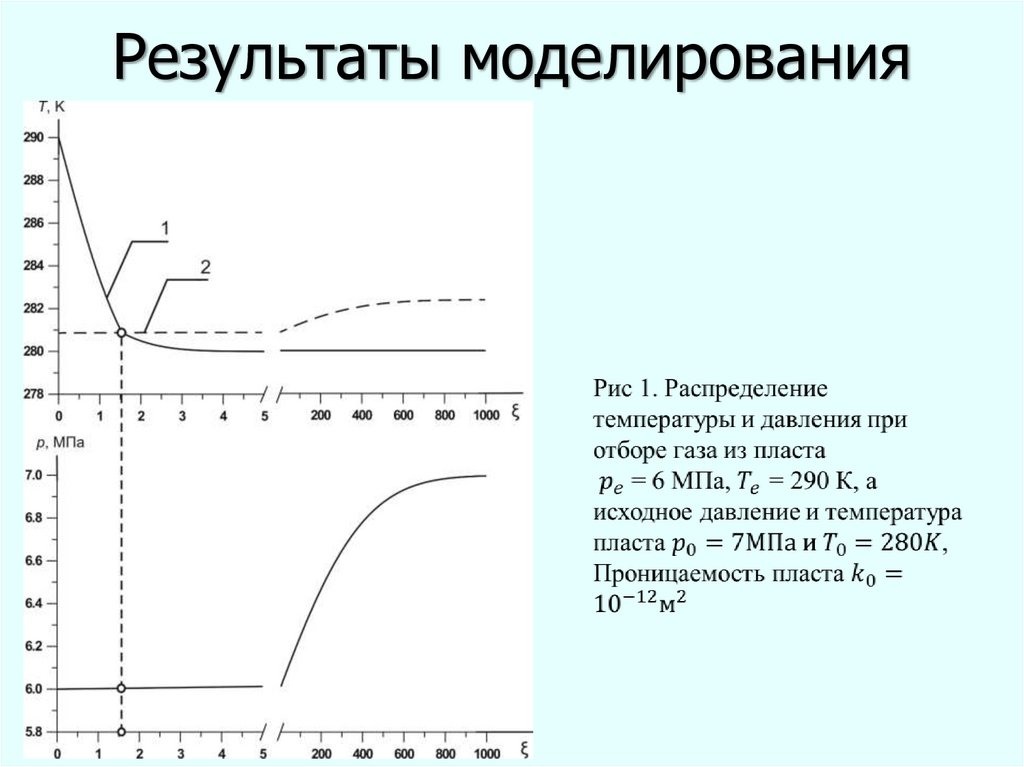
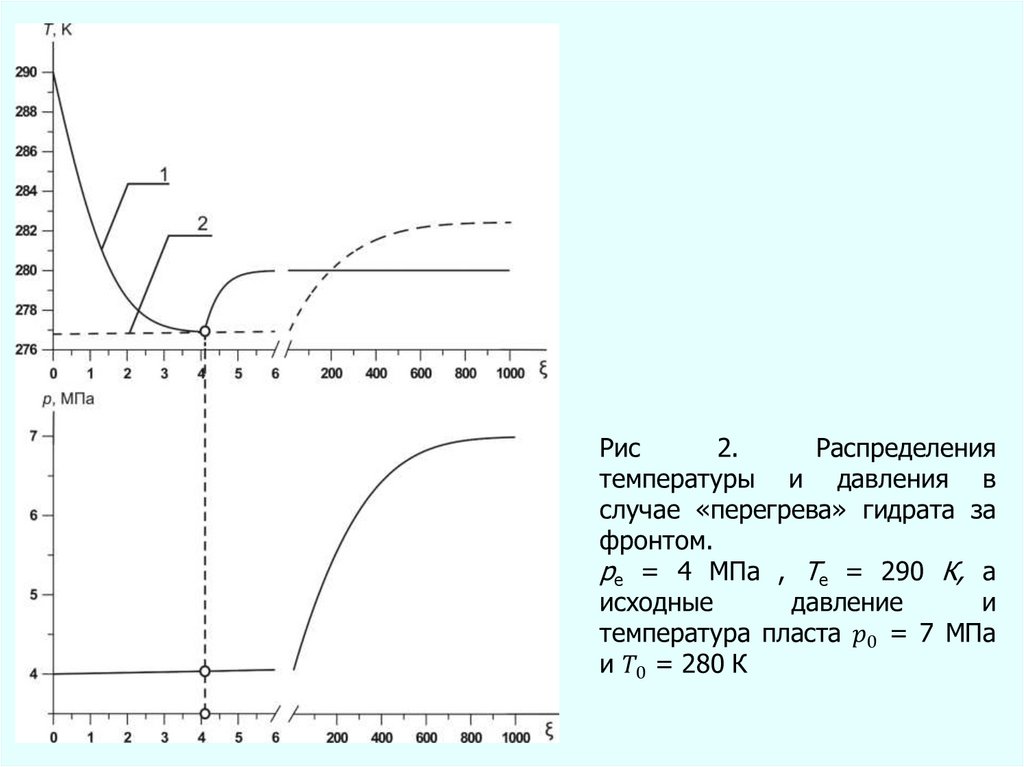
20. Результаты моделирования

21.

22.

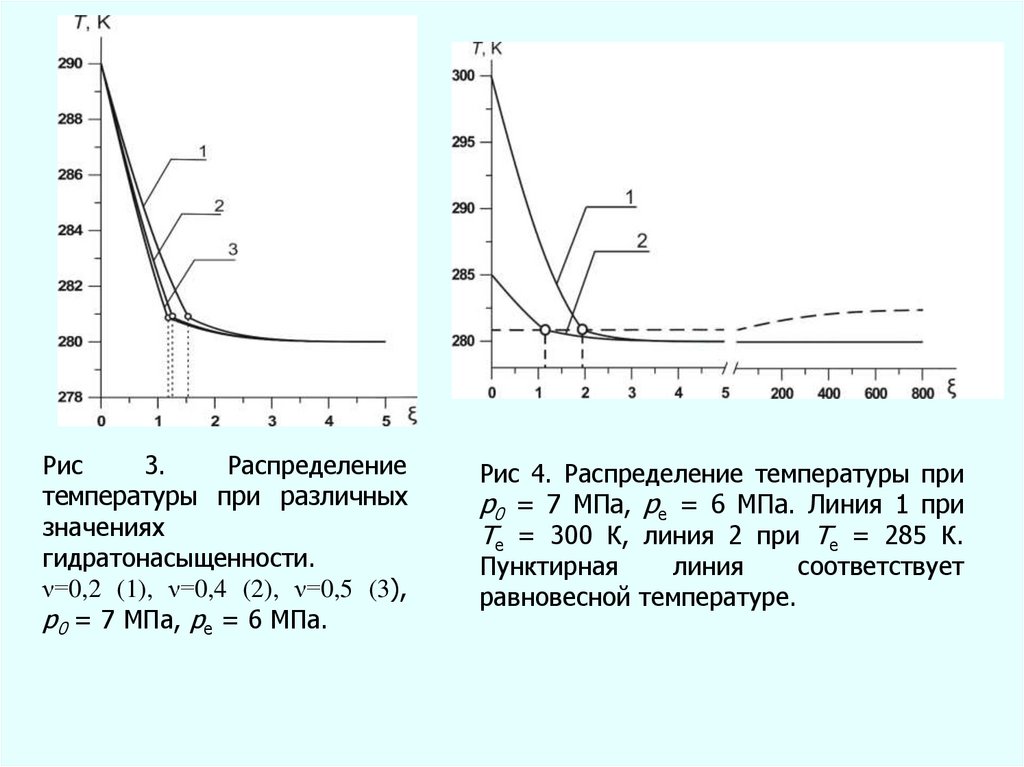
Рис
3.
Распределение
температуры при различных
значениях
гидратонасыщенности.
ν=0,2 (1), ν=0,4 (2), ν=0,5 (3),
p0 = 7 МПа, pe = 6 МПа.
Рис 4. Распределение температуры при
p0 = 7 МПа, pe = 6 МПа. Линия 1 при
Te = 300 К, линия 2 при Te = 285 К.
Пунктирная
линия
соответствует
равновесной температуре.

23.

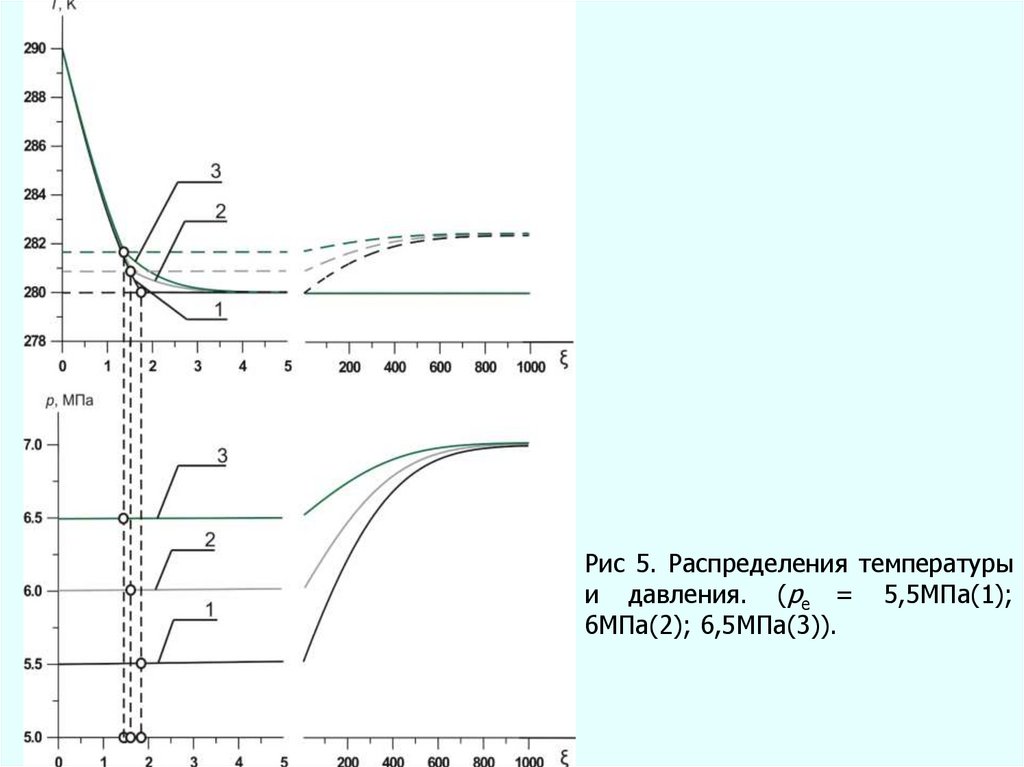
Рис 5. Распределения температуры
и давления. (pe = 5,5МПа(1);
6МПа(2); 6,5МПа(3)).

24.

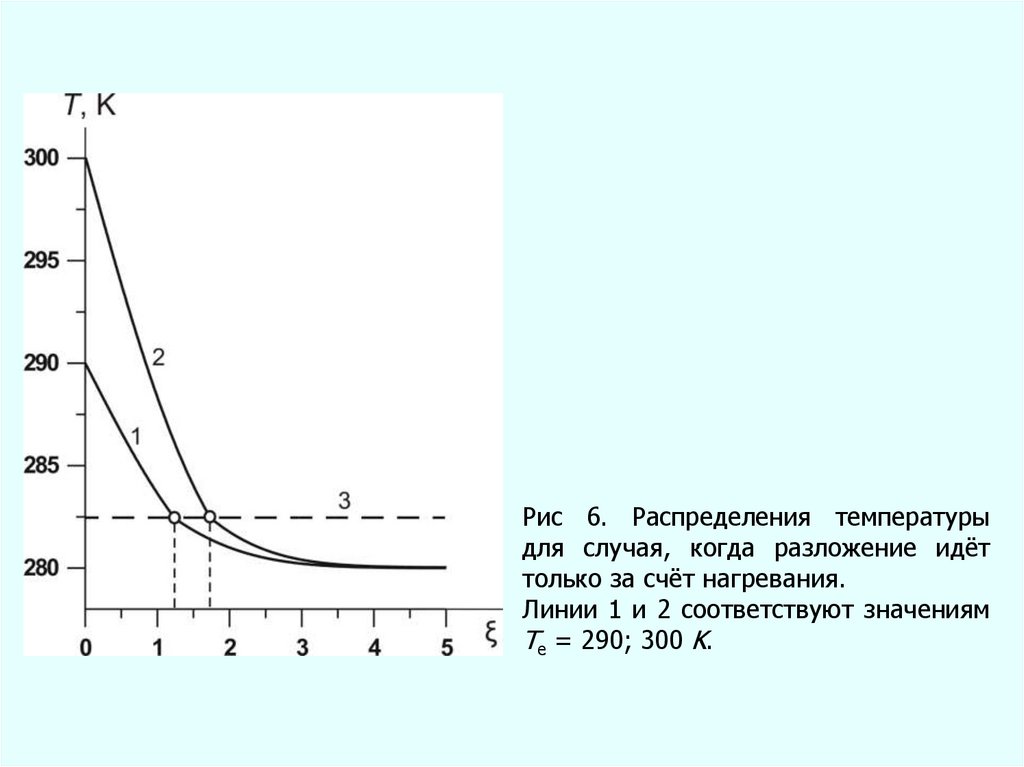
Рис 6. Распределения температуры
для случая, когда разложение идёт
только за счёт нагревания.
Линии 1 и 2 соответствуют значениям
Te = 290; 300 K.